1. 流れの概念¶
私たちが川の流れを考えるとき,
どのような光景が思い浮かぶでしょうか。
ある場所では狭くなったり,広くなったり,
あるいは深くなったり,浅くなったり,
流れは実にバラエティーに富んでいることがわかると思います。
このように,
場所によって速さや深さが変わるような流れのことを不等流といい,
これが今後,実際の水理現象を説明していく際に根幹となるものです。
なお,流れをもっと厳密に追求していくと,
時間的に変化するものが考えられ,
これを不定流といいます。
洪水流や感潮河川の流れが,代表的な不定流の例であります。
しかしながら,一般的な河川の流れは,
時間的な変化を考えない定流とみなしてもさしつかえなく,
かつその方が流れの性質をやさしく捉えやすいことから,
以後は原則として,定流について考えていくことにします。
さて,一見しで複雑な流れをどのように表現していけばよいでしょうか。
簡単にいうと,ある地点に水が流れるとき,
これを示すのに必要なのは,流体のおかれている位置の高さ(河床高),
水深そして流速の 3 つに過ぎません。
これらをもって,流れを表示したのが 図-1.1 です。
この図でわかるように,
流れを構成する 3 つの要素はすべて長さの次元,
つまり,水頭をもって表現していることがわかると思います。
例えば,流速ならば 2 乗して
\(2\mathrm{g}\)(\(\mathrm{g}\) は重力加速度で
9.8 m/s2)で割ってあります。
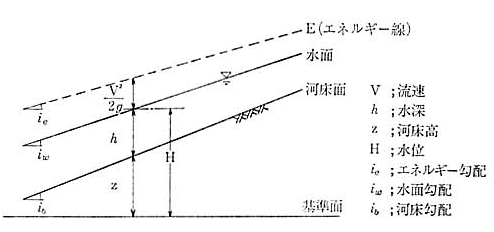
図-1.1 流れの表示
そして,各水頭をたし合わせたものが,そこで流体のもつ総水頭, いい換えるとエネルギーを表わしていることになります。 この地点・地点の総水頭を結んだものが, 図中の点線で示されるエネルギー線というものになるわけです。 つまり,エネルギー線は各地点における
ここで,\(z\):河床高 (m), \(h\):水深 (m), \(V\):流速 (m/s) で表わされる \(E\) を結んでいったものにほかありません。 また,流れの表示上,基準線と各種線の傾きを定義しておく必要があります。 図に示されるように, 河床の基準線(一般には水平)に対する傾きを河床勾配といい, \(i_b\) で,水面の基準線に対する傾きを水面勾配といい, \(i_w\) で, そしてエネルギー線が基準線となす傾きをエネルギー勾配といい, \(i_e\) で表わすこととします。