5. 河床変動計算の応用

中津川誠・清水康行

 われわれは，これまでの解説をとおして，流れや河床変動計算の基本的な考え方を学んできました。 また，多くの演習問題をとおして，水深や流速が変わる複雑な流れや， 流砂形態の違いをとりこんだ河床の変化も再現できることを理解しました。 ところが，実際の河川では山奥に源を発した流れがそのままの流量で延々と海まで達するものは稀で， 支川の合流や分流があるのがほとんどです。 また，よほどの山奥や未開地はともかく， われわれが扱うべき河川では治水対策上なんらかの手が人為的に加えられております。 床止めや帯工などがそのようなものに該当するでしょう。 つまり，1 本の川が高き所から低き所へと流下するという事実に， 上にあげたようなさまぎまな境界条件を加えたものを考慮して， はじめてさまざまな様相をみせる実河川の姿を再現できるといえるのです。
 以上のようなことから，最終章である第 5 章では， 今まで得られてきた流れや河床変動計算についての知識を応用して， より現実に近い河川への適用を試みたいと思います。
 なお，このほか実用を目指した河川水理の計算例では， 先に河川研究室から出された “パソコンを用いた一次元河床変動計算” ¹⁾ にも類例が報告されております。 内容については，河床材料の粒径がある分布をもっている場合の河床変動計算（混合粒径問題）また河道条件では河幅や勾配が変化する場合， せき上げの影響のあるような計算例も掲載されていますので，参考としていただければ幸いです。

5.1　床止めなどの横断工作物がある場合の計算

 河床洗掘の防止など安定河道維持を目的として， 床止めや帯工といった作工物が設置される例は多く見受けられます。 そのような場合の計算を，以下で考えてみましょう。
 基本的な考え方としては， 構造物上での河床変動はたまることはあっても， 設置時の高さより掘れていくことはないという土砂輸送の挙動に従っており， この事実を計算の制約条件の中に取込んでやればよいのです。
 簡単のため，流れは常流，流砂形態は掃流砂とします。 つまり，計算の際の差分形式は流砂連続式では時間的に前進差分， 空間的に後進差分をとることになります (3 章 3 節参照）。 手順としては，まず，不等流計算をやることになりますが， 方法としては，今までのやり方とまったく同様です。 ただし，床止め部の粗度は河床の粗度と違うので， マニングの粗度係数を別途検討評価しなければならないのですが， 本解説の中では単純化のため， 全川河床の粗度を一定として計算することとします。 次に，河床変動計算ですが，ここで先にいったように，一工夫必要です。 復習のため，図-5.1 のような河道における流砂連続式を差分形式で書いてみましょう (3 章 3 節 3 項，(24)式 参照)。

図-5.1　対象河道（床止めを含む場合）

(1)\[ \Delta z = -\frac{1}{1 - \lambda} \cdot \frac{Q_B(x, t) - Q_B(x - \Delta x, t)}{B(x) \cdot \Delta x} \Delta t \]

 ここで， \(\Delta z\)：断面 \(x\) の河床変動量， \(\lambda\)：河床材料空隙率（≒ 0.4)， \(Q_B(x, t)\)：断面 \(x\)，時間 \(t\) の全幅掃流砂量， \(B(x)\)：断面 \(x\) の断面幅， \(\Delta x\)：断面間距離， \(\Delta t\)：計算時間間隔， ただし，\(x\) は上流端を原点とし， 上流から下流の方向を正とする (図-3.6参照)。
 ここで求められる \(\Delta z\) が正のときは堆積， 負のときは洗掘を意味していることは前に述べました。 ところが，断面 \(x\) に床止めのある場合は洗掘が起きません。 つまり，\(\Delta z\) が負になるような場合は， 強制的に \(\Delta z\) を零にしてやる必要があります。 そのためには，(1)式から一見してわかるように右辺を 0 にすべく，

(2)\[ Q_B(x, t) = Q_B(x - \Delta x, t) \]

 これを単位幅流砂量の収支で表わせば，

\[ B(x) \cdot q_B(x, t) = B(x - \Delta x) \cdot q_B(x - \Delta x, t) \]

より，

(3)\[ q_B(x, t) = \bigl\{ B(x - \Delta x) / B(x) \bigr\} \cdot q_B(x - \Delta x, t) \]

 ここで，\(q_B(x,t)\)：断面 \(x\)，時刻 \(t\) の単位幅流砂量
というように，断面 \(x\) の流砂量を設定しなおす必要があります。 いわば，床止めがむきだしになっていればそれ以上河床が低下することはなく， そのためには 1 つ上流の流砂が全量通過するという収支関係を設定していることになるわけです。 なおこのほか，床止め上にいったん土砂が堆積してから掘れていくという状況も考えられますが， このときは，あくまでも床止めの高さを押さえておいて， それ以下には河床が抵下しないとの条件を加えてやればよいでしょう。 すなわち，

   \(\Delta z < 0\)，\(|\Delta z| > |\Delta z'|\) のとき，\(\Delta z'\) を河床変動高とする

 ここで，\(\Delta z\)：(1)式で計算される河床変動量，\(\Delta z'\)：現河床高と床止めの高さの差
とします。そして，上記条件に見合う流砂量は(1)式より下式で表わすことができます。

(4)\[ Q_B(x, t) = -(1 - \lambda) \cdot B(x) \cdot \Delta x \cdot \Delta z' / \Delta t + Q_B(x - \Delta x, t) \]

 以上のように，床止めを含む河川では河床変動量に条件をつけ，それに即した流砂量を定めてもう一度計算を やりなおしてやることで再現が可能になるわけです。 一連の計算条件や手順は，図-5.2，図-5.3 に整理しておきますので， 参考にして下さい。
 なお，射流の場合も計算の流れや，床止めの扱いは同じです。 ただし，不等流計算における逐次計算の向きや流砂連続式の差分法は以前に示したように，適宜変えてやる必要があります。

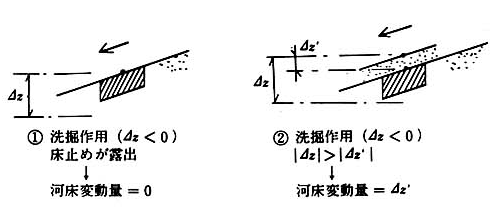
図-5.2　床止め上での制約条件

図-5.3　床止めのある場合の計算手順

5.2　合流点を含む場合の計算

 河川の水理現象を表わす場合， 欠かすことのできないものとして，合流点の問題があります。 ところで，合流点の不等流計算を厳密に行う場合，むずかしくいうと， 運動量の概念が必要となってきます。 すなわち，今まで習得してきたエネルギー収支を表わす方程式は， 合流に伴なう損失を明確に表現できないという欠点をもっております。 しかしながら，本解説の目的たる現場での容易な実用化を目指すとの意昧から， 繁雑な運動量による取扱いを避けた方が無難に思われます。 よって，これまで学んできたものを最大限に生かし， 無理のない範囲での仮定を設けたいわば試算例という位置づけで解説を行っていこうと思います。
 対象としては，図-5.4 に示されるような河川を考えることとします。

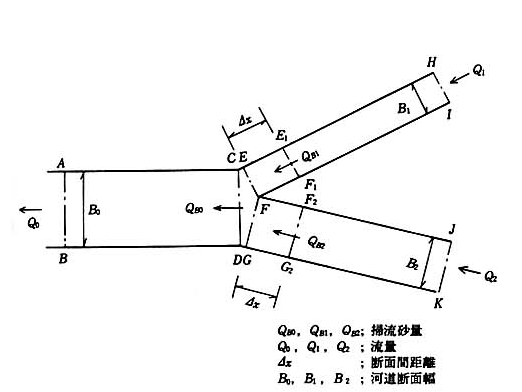
図-5.4　対象河道（合流点を含む場合）

 この場合も考えやすいように，流れは常流，流砂は掃流砂として， まず，流れの計算の手順を示します。

1. 本川 \(ABCD\) 部分の不等流計算を，下流端水位 \(H_{AB}\) を起算水位として行う。

2. 支川 \(EFHI\) 部分，支川 \(FGJK\) 部分の不等流計算を，各々の下流端水位水位 \(H_{EF}\)，\(H_{FG}\) を起算水位として行う。

3. 1. および 2. から求められた水理量，河床材料の性状より流砂量 \(Q_B\) を算出する。
      

4. 流砂量 \(Q_B\) の収支から，河床変動計算を行う。

 ステップ 2 において，合流部の五角形 \(CDEFG\) で囲まれた部分の水位は， 近似的に等しいと仮定します (仮定 1)。すなわち，

\[ H_{CD} = H_{EF} = H_{FG} \]

として，2. の計算をやればよいわけです。なお，このとき

(5)\[ Q_0 = Q_1 + Q_2 \]

で示される連続条件が満たされています。 ここで，\(Q_0\)：合流後の流量，\(Q_1\)，\(Q_2\)：合流前の流量
 次にステップ 4 の合流点の河床変動計算ですが，「断面 \(E_1F_1\) の流砂量 \(Q_{B1}\) と，断面 \(F_2 G_2\) の流砂量 \(Q_{B2}\) が断面 \(CD\) の流砂量 \(Q_{B0}\) と連続条件を満たす」とします (仮定 2)。また，このときの対象断面間距離としては， 断面 \(EF\) と断面 \(E_1 F_1\) ないし断面 \(FG\) と断面 \(F_1 G_1\) の距離を考えることとします。 計算の便宜上，両者は同一にしておいた方がよいでしょう。

 以上のことを勘案して，合流部 \(CD\) の河床変動量を算出するための流砂連続式は，

(6)\[ \Delta z = -\frac{1}{1 - \lambda} \cdot \frac{Q_{B0} - (Q_{B1} + Q_{B2})}{B_0 \cdot \Delta x} \]

と表わすことができます。 ここで，\(\Delta z\)：断面 \(CD\) の河床変動量， \(\Delta x\)：断面間距離， \(\lambda\)：河床材料空隙率， \(B_0\)：断面 \(CD\) の断面幅， \(Q_{B0}\)：断面 \(CD\) の流砂量， \(Q_{B1}\)：断面 \(E_1 F_1\) の流砂量， \(Q_{B2}\)：断面 \(F_2 G_2\) の流砂量
 すなわち，(6)式は平面 \(CDEFG\) 内では河床変動量が同一という条件が満たされることを意味し， これは，先に掲げた 仮定 2 をいい換えたものにほかありません。
 以上，合流点を含む河川の計算手法を示してきましたが，この手順を 図-5.5 に整理しておきます。 前にも述べたように，合流時は渦によるエネルギーの逸散など不明確な点があり， 1 次元的に流れを捉える場合，どうしても合流部の水理現象に仮定が必要となってきます。 本法では，これを五角形 \(CDEFG\) の水理現象は， その中のいたるところで均等に生じ， しかも下流側断面 \(CD\) のそれに規定されるとの仮定を設け， 計算の単純化，簡易化を図っているわけです。

図-5.5　合流点のある場合の計算手順

演習問題 21

 河口からの距離およ川幅が下表に示されるような河川において， 流量 1,000 m³/s が 48 時間流下した場合の河床変動量を求めよ。
 ただし，河口水位を 0 m (一定)， 河床材料の粒径 \(d\) = 2 cm， 粗度係数 \(n\) = 0.025， 流砂は掃流砂のみとし， 流砂量式は \(q_b / \sqrt{s g d^3} = 8 (\tau_* - \tau_{*c})^{1.5}\) を用いること。また，断面は矩形とする。

1. 上流端での流砂量は，動的平衡状態である（すなわち，上流端の河床変動はないとして計算せよ。

2. 上流端にダムがあるとしで計算せよ (ダム地点では流砂量 ＝ 0)。

3. 上記 1. において，K.P.2.6 地点に床止めがある場合の計算をせよ。

4. 上記 1. において，K.P.2.2, 2.6, 3.0 に床止めがある場合の計算をせよ。

河道条件 [m]

\(x\)	\(B\)	\(z\)	\(x\)	\(B\)	\(z\)
0.0	300	-2.0	2.4	220	2.8
0.2	300	-1.6	2.6	220	3.2
0.4	300	-1.2	2.8	220	3.6
0.6	300	-0.8	3.0	220	4.0
0.8	300	-0.4	3.2	220	4.4
1.0	300	0.0	3.4	300	4.8
1.2	300	0.4	3.6	300	5.2
1.4	300	0.8	3.8	300	5.6
1.6	300	1.2	4.0	300	6.0
1.8	300	1.6	4.2	300	6.4
2.0	300	2.0	4.4	300	6.8
2.2	220	2.4

解答例

演習問題 22

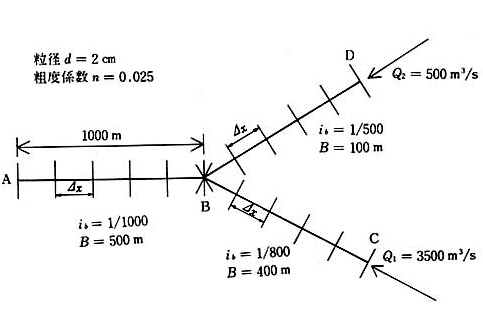
 下図に示す河川に， 上流端Cから流量 \(Q_1\) = 3,500 m³/s， \(D\) から流量 \(Q_2\) = 500 m³/s の流入があった場合の 5 日後の河床縦断形状を求めよ。 ただし，\(A-B\) 間，\(B-C\) 間はそれぞれ 1,000 m とする。 また，境界条件として下流端 \(A\) の水深は等流水深で与え， 上流端 \(C\) の流砂量は \(\partial Q_B / \partial x\) = 0， \(D\) では \(Q_B\) = 0 を与える。
 計算条件は \(\Delta x\) = 200 m， \(\Delta t\) = 600 s とする。

解答例

---

参考文献

1) 福田義昭：パソコンを用いた一次元河床変動計算，土木試験所月報． No.398, 1986 年 7 月.