4. 浮遊砂と河床変勤

荒井信行・清水康行

 第 3 章で述べたように， 浮遊砂は乱流拡散現象によって輸送される形式の流砂である。 浮遊砂を含む流れは， 例えばダム貯水池の堆砂や河口部浚渫個所などの洪水による多量の土砂堆積等に見られるように， 河床変動に大きな影響を与え，実際上も重要な問題であるため， これまで浮遊砂に関して数多くの研究がなされてきた。 それらの研究は，大別すると浮遊砂流の特性に関するものと土砂の輸送量に関するものがある。
 今回は，主に均一粒径砂を対象とした浮遊砂量式と浮遊砂による 1 次元単断面の河床変動の問題に重点をおいて述べることにする。
 なお，浮遊砂に関する諸問題は，複雑， かつ広範多岐にわたるため， 上記の研究成果は多くの仮定や近似的取扱いに基づいており， 未解明の問題も多く残されているのが現状である。 このような状況から，本章では実際間題として一般的な適用性を失なわない程度に問題を簡略化して解説するつもりである。

4.1　浮遊砂の基準点濃度と砂粒の浮上量式

 浮遊砂の濃度 \(c\) は，容積表示で次のように定義される。 いま，流量を \(Q\) (m³/s)， その流量中の浮遊砂量を \(Q_s\) (m³/s) とすると， \(c = Q_s / Q\) である。 図-4.1 のように，定常 2 次元等流を考えた場合の単位幅当たりの浮遊砂量 \(q_s\) (m³/s/m) は， 濃度分布 \(c(z)\) および流速分 \(u(z)\) が決定されれば， 次式で与えられる。

(1)\[ q_s = \int_b^h \! c(z) \, u(z) \,dz \]

 ここに，\(h\)：水深， \(c(z)\)：河床面上 \(z\) の点における濃度， \(u(z)\)：河床面上 \(z\) の点における流速， \(b\)：濃度の基準点とされる河床面からの高さであり， \(b\) のとり方により濃度分布が若干異なってくる。

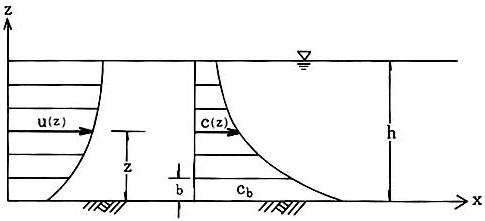
図-4.1　流速分布 \(u(z)\) および濃度分布 \(c(z)\) の定義図

 浮遊砂量の算定は， 濃度の基準点 \(b\) の値とその点の濃度 \(c_b\) の算定の問題に帰着する。 一般的には，\(b\) の値は水深の 5 %，すなわち \(b = 0.05 h\) が採用されている。 また，浮遊砂の基準点濃度および砂粒の浮上量式としては， 以下の板倉の式¹⁾を紹介する。 板倉は，河床が平担な場合の浮遊砂を含む開水路流れについて， 流速分布，浮遊砂の濃度分布，浮遊砂の基準点濃度，浮遊砂流の抵抗特性， 浮遊砂量式，堆積限界を一貫した理論によって系統的に導いている。 詳細は原論文を参照されたい。
 いま，河床が均一砂粒で構成されている場合を考える。 河床が平衡状態にあるとき， 河床の単位面積から単位時間に巻き上がる粒子群の体積 \(q_{su}\) (m/s) は， 単位面積当たり単位時間に河床へ沈降する粒子群の体積 \(w_f \cdot c_b\) (m/s) に等しいので，次式がなりたつ。

(2)\[ q_{su} = w_f \cdot c_b \]

 ここで，浮遊砂の底面付近 (\(z = b\)) の濃度， すなわち基準点濃度 \(c_b\) は，

(3)\[ c_b = K \left( \alpha_* \frac{\rho_s - \rho}{\rho_s} \cdot \frac{\mathrm{g} d}{u_* w_f} \Omega - 1 \right) \]

と書き表わされ，\(q_{su}\) は次式により与えられる。

(4)\[ \frac{q_{su}}{\sqrt{s \mathrm{g} d}} = K \left( \alpha_* \frac{\rho}{\rho_s} \cdot \frac{\Omega}{\sqrt{\tau_*}} - \frac{w_f}{\sqrt{s \mathrm{g} d}} \right) \]

(5)\[ \Omega = \frac{\tau_*}{B_*}\frac{\displaystyle{ \int_{a'}^{\infty} \xi \frac{1}{\sqrt{\pi}} \exp (-\xi^2) \, d\xi }}{\displaystyle{ \int_{a'}^{\infty} \frac{1}{\sqrt{\pi}} \exp (-\xi^2) \, d\xi }} + \frac{\tau_*}{B_* \eta_0} - 1 \]

\[ a' = \frac{B_*}{\tau_*} - \frac{1}{\eta_0} \,,\quad \eta_0 = 0.5 \,,\quad \alpha_* = 0.14 \,,\quad K = 0.008 \,,\quad B_* = 0.143 \]

 ただし， \(\rho_s\)：砂粒の密度，\(\rho\)：水の密度，\(s\)：砂の水中比重， \(\mathrm{g}\)：重力加速度，\(d\)：砂粒の粒径，\(w_f\)：砂粒の沈降速度
 また，(4)式の近似式として次式がある。

(6)\[ \frac{q_{su}}{\sqrt{s \mathrm{g} d}} = 0.008 \left[ 0.14 \frac{\rho}{\rho_s} \left( 14 \sqrt{\tau_*} - \frac{0.9}{\sqrt{\tau_*}} \right) - \frac{w_f}{\sqrt{s \mathrm{g} d}} \right] \]

4.2　浮遊砂濃度の連続式と河床変動の連統式

 問題を簡単にするために， 以後浮遊砂の濃度 \(c\) として次式で定義される水深方向の平均濃度 \(\bar{c}\) を用いて議論を進める。 すなわち，\(c = \bar{c}\) とする。

(7)\[ \bar{c} = \frac{q_{su}}{q} = \frac{\displaystyle{\int_b^h c(z) u(z) \,dz}} {\displaystyle{\int_b^h u(z) \, dz}} \]

 まず，浮遊砂濃度の連続式を誘導してみよう。 ただし，本節では濃度 \(c\) はある時間 \(\Delta t\) の間では一定として扱い， 拡散作用を無視する。

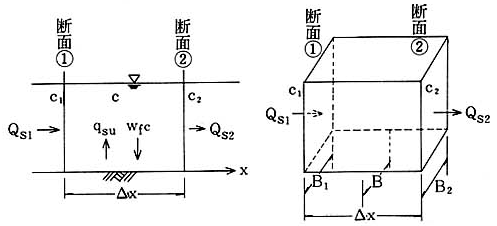
図-4.2　浮遊砂濃度の連続式

 いま，図-4.2 に示すように主流方向に \(x\) 軸をとると， 微小時間 \(\Delta t\) の間に断面 ① から入ってくる浮遊砂量は， \(Q_{s1} \cdot \Delta t = Q \cdot c_1 \cdot \Delta t\) であり， 同様に \(\Delta t\) の間に断面 ② からでていく浮遊砂量は， \(Q_{s2} \cdot \Delta t = Q \cdot c_2 \cdot \Delta t\) である。 次に，断面 ①，② 間で \(\Delta t\) の間に浮上する砂量および沈降する砂量は， それぞれ \(q_{su} \cdot B \cdot \Delta x \cdot \Delta t\) および \(w_f \cdot c \cdot B \cdot \Delta x \cdot \Delta t\) である。
 したがって，断面 ①，② 間でこれらの砂量の収支が 0 となるためには，

(8)\[ Q c_1 \Delta t - Q c_2 \Delta t + q_{su} \cdot B \cdot \Delta x \cdot \Delta t - w_f \cdot c \cdot B \cdot \Delta x \cdot \Delta t = 0 \]

 ゆえに，

\[ \frac{Q (c_2 - c_1)}{B \cdot \Delta x} = q_{su} - w_f \cdot c \]

となる。上式を微分方程式で表わすと，

(9)\[ \frac{Q}{B} \cdot \frac{dc}{dx} = q_{su} - w_f \cdot c \]

となる。(9)式が浮遊砂濃度の連続式である。
 ここで，特別な場合として流下方向に濃度が一定 (平衡状態)， すなわち \(dc/dx = 0\) とすると，(9)式の右辺 = 0 であるから， \(c = q_{su} / w_f\) となる。
 実際に(9)式により流下方向の濃度分布を計算する場合には， 左辺の \(dc/dx\) の差分形が問題となる。 いま，(9)式を後進差分で計算することを考えてみる。
 (9)式の差分式は，

\[ \frac{Q}{B(x)} \cdot \frac{c(x) - c(x - \Delta x)}{\Delta x} = q_{su}(x) - w_f \cdot c(x) \]

であるから，\(c(x)\) について整理すると，次式となる。

(10)\[ c(x) = \frac{\displaystyle{ q_{su}(x) + c(x - \Delta x) \frac{Q}{B(x) \cdot \Delta x} }}{\displaystyle{ \frac{Q}{B(x) \cdot \Delta x} + w_f }} \]

 したがって，各断面における砂粒の浮上量 \(q_{su}(x)\)， 砂粒の沈降速度 \(w_f\) が求まり， 境界条件として上流端の濃度 \(c(0)\) が与えられれば， (10)式により各断面の濃度 \(c(x)\) を計算することができる。
 次に，浮遊砂による河床変動の連統式を誘導する。

図-4.3　浮遊砂による河床変動の連続式

 図-4.3 に示すように， ある時刻 \(t\) から微少時間 \(\Delta t\) の間に河床から浮上する砂量および河床へ沈降する砂量は， それぞれ \(q_{su} \cdot B \cdot \Delta x \cdot \Delta t\) および \(w_f \cdot c \cdot B \cdot \Delta x \cdot \Delta t\) である。 いま河床が低下する場合を考えると，流水中の砂粒の増加量は，

\[ (q_{su} - w_f \cdot c) \cdot B \cdot \Delta x \cdot \Delta t \]

であり，これは河床から流水中にでていく砂量，すなわち河床低下量に等しい。
 河床低下量は，河床変動高を \(\Delta z\)， 空隙率を \(\lambda\) とすると，

\[ -\Delta z \cdot B \cdot \Delta x \cdot (1 - \lambda) \]

で表わされるから，上記の 2 式を等しいとおくと，次式が得られる。

\[ \frac{\Delta z}{\Delta t} = -\frac{1}{1 - \lambda} (q_{su} - w_f \cdot c) \]

 上式を微分方程式で表わすと，

(11)\[ \frac{dz}{dt} = -\frac{1}{1 - \lambda} (q_{su} - w_f \cdot c) \]

となる。 (11)式が浮遊砂による河床変動の連続式である。

4.3　非定常性を考慮した浮遊砂濃度の連続式

 前出の浮遊砂濃度の連統式(9)式は， 微小時間 \(\Delta t\) の間で濃度 \(c\) を一定として取扱った場合の式である。 しかしながら，実際問題では多くの場合濃度 \(c\) が時間的に一定とは考えにくく， 例えば演習問題 18で示すように， ダム貯水池へ浮遊砂が流入するような場合には， 前記の計算法では初期条件， すなわち時刻 \(t = 0\) の段階で全断面で濃度 \(c\) があることとなるのに対して， 実際には時刻 \(t = 0\) ではすべての断面で \(c = 0\)， すなわち清水という条件があり得る。
 そこで，本節では濃度 \(c\) の時間変化を考慮した浮遊砂濃度の運続式を誘導する。 前出の 図-4.2 より，ある時刻 \(t\) における濃度を \(c(t)\), \(\Delta t\) 時間後の濃度を \(c(t + \Delta t)\) とすると， \(\Delta t\) 時間の間の断面 ①，② 間における流水中の浮遊砂の増加量は， 次のように表わされる。

\[ c(t + \Delta t) \cdot B \cdot h \cdot \Delta x - c(t) \cdot B \cdot h \cdot \Delta x \]

 ここで，濃度 \(c\) の変化量を \(\Delta c = c(t + \Delta t) - c(t)\) とおくと，上式は，

\[ \Delta c \cdot B \cdot h \cdot \Delta x \]

となる。
 断面 ①，② の間の砂量の収支を考えると，前出の(8)式の左辺が \(\Delta c \cdot B \cdot h \cdot \Delta x\) に等しいことから， 次式が得られる。

(12)\[ Q c_1 \Delta t - Q c_2 \Delta t + q_{su} \cdot B \cdot \Delta x \cdot \Delta t - w_f \cdot c \cdot B \cdot \Delta x \cdot \Delta t = \Delta c B h \Delta x \]

 (12)式の両辺を \(B \cdot \Delta x \cdot \Delta t\) で割ることにより，次式が導かれる。

\[ h \frac{\Delta c}{\Delta t} + \frac{Q}{B} \cdot \frac{c_2 - c_1}{\Delta x} = q_{su} - w_f \cdot c \]

 上式を微分方程式で表わすと，

(13)\[ h \frac{\partial c}{\partial t} + \frac{Q}{B} \cdot \frac{\partial c}{\partial x} = q_{su} - w_f \cdot c \]

となり，上式が非定常性を考慮した浮遊砂濃度の連続式である。
 ここで，(13)式を時間 \(t\)，距離 \(x\) に関して差分表示することを考える。
 まず，(13)式より \(\Delta t\) 時間後の濃度 \(c(t + \Delta t)\) を求める式として，次式が得られる。

(14)\[ c(t + \Delta t) = c(t) + \frac{\Delta t}{h} \left( q_{su} - w_f \cdot c - \frac{Q}{B} \cdot \frac{\partial c}{\partial x} \right) \]

 (14)式により，時刻 \(t\) における流下方向の濃度分布から \(\Delta t\) 時間後の濃度分布を求める際に問題となるのは， \(\partial c / \partial x\) の差分形のとり方である。
 いま，後進差分の場合を考えると， (14)式における濃度 \(c\) は \(x\) と \(t\) の関数なのでより丁寧に書くと，(14)式は次式となる。

(15)\[ c(x, t + \Delta t) = c(x, t) + \frac{\Delta t}{h} \left\{ q_{su} - w_f \cdot c - \frac{Q}{B} \cdot \frac{c(x, t) - c(x - \Delta x, t)}{\Delta x} \right\} \]

(15)式が求める(13)式の差分式である。
 また，定常等流状態の流れを考えると， (13)式は次式のように変形される。 (13)式の両辺を水深 \(h\) で割り， \(x\) 軸方向の平均流速 \(u = Q / Bh\) (一定) とおくと，

(16)\[ \frac{\partial c}{\partial t} + u \frac{\partial c}{\partial x} + \frac{w_f \cdot c}{h} = \frac{q_{su}}{h} \]

となる。(16)式を移流方程式と呼んでいる。
 一般に，(16)式のような形式の偏微分方程式においては， 特性曲線は \(dx / dt = u\) となり， \(\partial c / \partial x\) の差分形式は流速 \(u\) と同方向， すなわち流下方向に向いた差分形である後進差分とする必要がある。

4.4　拡散項を含む浮遊砂濃度の連統式

 図-4.4 において，断面 ① における濃度 \(c_1\)， 断面 ② における濃度を \(c_2\) とすると， \((c_2 - c_1) / \Delta x = dc / dx\) を濃度勾配という。
 一般に，2 地点間に濃度勾配があるとき， すなわち 2 地点間で濃度に差があるときには， 濃度勾配に比例した物質移動が，その差をなくす方向に生ずる。 その移動量は，比例定数を \(D\) とすると \(-D \, dc/dx\) と表わされる。 この \(D\) を拡散係数という。

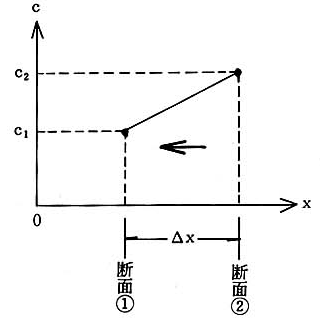
図-4.4　濃度勾配 (矢印は浮遊粒子の移動方向)

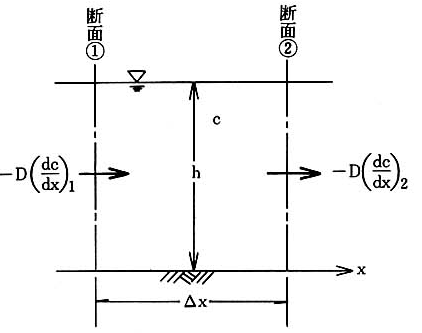
図-4.5　拡散作用による浮遊砂の濃度変化

 いま，図-4.5に示すように流速ゼロの状態， すなわち静水中を考える。
 断面 ① から微小時間 \(\Delta t\) の間に拡散作用により流入する浮遊砂量は，

\[ -D \left( \frac{dc}{dx} \right)_{\!\!1} \cdot h \cdot B \cdot \Delta t \]

であり，断面 ② から \(\Delta t\) 時間に流出する浮遊砂量は，

\[ -D \left( \frac{dc}{dx} \right)_{\!\!2} \cdot h \cdot B \cdot \Delta t \]

である。一方，断面 ① ，② の間で \(\Delta t\) 時間に濃度が \(c(t)\) から \(c(t+\Delta t)\) に変化するとすれば， その変化量は，

\[ \bigl\{ c(t + \Delta t) - c(t) \bigr\} \cdot h \cdot B \cdot \Delta x \]

で与えられる。ここで，断面 ①，② 間の砂量の収支を考えると，

\[ \left\{ c(t + \Delta t) - c(t) \right\} \cdot h \cdot B \cdot \Delta x = D \left( \frac{dc}{dx} \right)_{\!\!2} \cdot h \cdot B \cdot \Delta t -D \left( \frac{dc}{dx} \right)_{\!\!1} \cdot h \cdot B \cdot \Delta t \]

 ゆえに，

\[ \frac{c(t + \Delta t) - c(t)}{\Delta t} = D \frac{\displaystyle{ \left( \frac{dc}{dx} \right)_{\!\!2} - \left( \frac{dc}{dx} \right)_{\!\!1} }}{\Delta x} \]

 上式を微分方程式で表わすと，

(17)\[ \frac{\partial c}{\partial t} = D \frac{\partial^2 c}{\partial x^2} \]

となる。(17)式を拡散方程式という。
 したがって，実際河川における浮遊砂濃度の連統式は，(16)式と(17)式をあわせて考えると， 次式により表わされる。

(18)\[ \frac{\partial c}{\partial t} + u \frac{\partial c}{\partial x} + \frac{w_f \cdot c}{h} = D \frac{\partial^2 c}{\partial x^2} + \frac{q_{su}}{h} \]

4.5　水深方向の浮遊砂濃度分布

 これまでは，浮遊砂量 \(Q_s\) を流量 \(Q\) と水深方向の平均濃度 \(c \,(= \bar{c})\) の積として求めてきたが， 実際には 第 1 節で述べたように， 濃度 \(c\) は水深方向の分布を考える必要がある。 例えば，前出の 図-4.2 のように河床からの砂の出入りを考える場合の沈降量 \(w_f \cdot c\) における \(c\) は， 平均濃度 \(\bar{c}\) ではなく，河床底面付近の濃度， すなわち基準点濃度 \(c_b\) を用いなければならない。
 いま，定常 2 次元等流状態の流れを考え， 流下方向には濃度変化はないものとする。

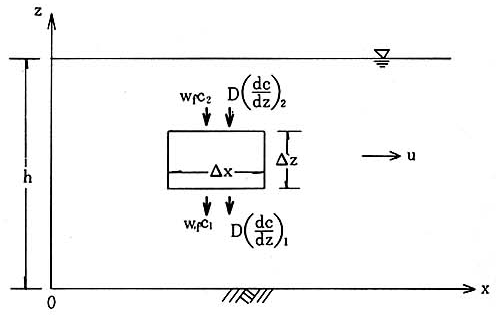
図-4.6　水深方向の浮遊砂の濃度変化

 図-4.6 に示したような微小要素 \(\Delta z \cdot \Delta x\) 内に， 微小時間 \(\Delta t\) 間に拡散作用により流入する浮遊砂量は，

\[ \left( D \frac{\partial c}{\partial z} \right)_{\!\!2} \cdot \Delta x \cdot \Delta t \]

であり，同様に流出する浮遊砂量は

\[ \left( D \frac{\partial c}{\partial z} \right)_{\!\!1} \cdot \Delta x \cdot \Delta t \]

である。
 また，微小要素 \(\Delta z \cdot \Delta x\) 内に \(\Delta t\) 間に流入する沈降量は，

\[ w_f \cdot c_2 \cdot \Delta x \cdot \Delta t \]

であり，微小要素 \(\Delta z \cdot \Delta x\) から流出する沈降量は，

\[ w_f \cdot c_1 \cdot \Delta x \cdot \Delta t \]

である。
 以上の砂量の収支を考えると，

\[ \left\{ \left( D \frac{\partial c}{\partial z} \right)_{\!\!2} - \left( D \frac{\partial c}{\partial z} \right)_{\!\!1} \right\} + w_f \bigl( c_2 - c_1 \bigr) = 0 \]

となるので，両辺を \(\Delta z\) で割って微分方程式で表示すると， 次式が得られる。

(19)\[ D \frac{d}{dz} \left( \frac{dc}{dz} \right) + w_f \frac{dc}{dz} = 0 \]

 通常，平担河床では(19)式中の拡散係数 \(D\) は渦動粘性係数 \(\varepsilon\) に等しく考える。 この \(\varepsilon\) を次式で定義する。

(20)\[ \varepsilon = \frac{\kappa}{6} u_* h \]

 ただし，\(\kappa\)：カルマン定数， \(h\)：水深，\(u_*\)：摩擦速度
 したがって，(19)式は次式に書換えられる。

(21)\[ \varepsilon \frac{d}{dz} \left( \frac{dc}{dz} \right) + w_f \frac{dc}{dz} = 0 \]

 上式を \(z\) で積分すると，

\[ \varepsilon \frac{dc}{dz} + w_f \cdot c + A_1 = 0 \]

であり，積分定数 \(A_1\) は水面における条件， すなわち水面 \(z = h\) では水面から浮遊砂粒子が飛びだすことはないので， \(dc/dz= 0\)，\(w_f \cdot c = 0\) であるから，\(A_1 = 0\) となる。
 ゆえに，上式は次式で表わされる。

(22)\[ \varepsilon \frac{dc}{dz} + w_f \cdot c = 0 \]

 上式を積分すると，

\[ \int \frac{dc}{c} = \int \left( -\frac{w_f}{\varepsilon} \right) \, dz \]

 ゆえに，

\[ \ln c = -\frac{w_f}{\varepsilon} z + A_2 \]

 または，

\[ c = A_3 \exp \left( -\frac{w_f}{\varepsilon} z \right) \]

となる。ここで，基準点濃度 \(c_b\) を近似的に河床面上 (\(z \sim 0\)) の濃度と考えると， \(A_3 = c_b\) であるから， 濃度 \(c\) は次式で与えられることになる。

(23)\[ c = c_b \exp \left( -\frac{w_f}{\varepsilon} z \right) \]

 上式が浮遊砂の濃度分布式である。
 これに対して， 前節までで使用していた濃度 \(c\) は河床から水面までの平均濃度である。 (23)式により平均濃度 \(\bar{c}\) を求めると，

\[\begin{split} \begin{align*} \bar{c} &= \frac{1}{h} \int_0^h c \,dz = \frac{1}{h} \int_0^h c_b \exp \left( -\frac{w_f}{\varepsilon} z \right) dz \\&= \frac{c_b}{h} \left[ -\frac{\varepsilon}{w_f} \exp \left( -\frac{w_f}{\varepsilon} z \right) \right]_0^h \\&= -\frac{\varepsilon c_b}{w_f \cdot h} \left\{ \exp \left( -\frac{w_f}{\varepsilon} h \right) - \exp \left( -\frac{w_f}{\varepsilon} \cdot 0 \right) \right\} \\&= \frac{\varepsilon c_b}{w_f \cdot h} \left\{ 1 - \exp \left( -\frac{w_f \cdot h}{\varepsilon} \right) \right\} \end{align*} \end{split}\]

 ここで，\(\beta = w_f \cdot h / \varepsilon\) とおくと， 次式が得られる。

(24)\[ \bar{c} = \frac{c_b}{\beta} \bigl( 1 - e^{-\beta} \bigr) \]

 上式が平均濃度 \(\bar{c}\) と基準点濃度 \(c_b\) の関係式である。 したがって，上式より基準点濃度は次式のように書き表わされる。

(25)\[ c_b = \frac{\beta}{1 - e^{-\beta}} \bar{c} \]

4.6　実際河川の浮遊砂による河床変動計算法

 前節で述べたように， これまで河床への沈降量は \(w_f \cdot c\) としてきたが， 実際には \(w_f \cdot c_b\) であるので， (18)式および(25)式より実際河川における浮遊砂濃度の連続式として最終的に次式が得られる。

(26)\[ \frac{\partial c}{\partial t} + u \frac{\partial c}{\partial x} + \frac{w_f}{h} \frac{\beta}{1 - e^{-\beta}} c = D \frac{\partial^2 c}{\partial x^2} + \frac{q_{su}}{h} \]

 既述のように，上式で拡散項を無視すると，次式が得られ，

(27)\[ \frac{\partial c}{\partial t} + u \frac{\partial c}{\partial x} + \frac{w_f}{h} \frac{\beta}{1 - e^{-\beta}} c = \frac{q_{su}}{h} \]

 さらに，濃度の時間変化を無視すると，次式となる。

(28)\[ u \frac{\partial c}{\partial x} + \frac{w_f}{h} \frac{\beta}{1 - e^{-\beta}} c = \frac{q_{su}}{h} \]

 また，浮遊砂による 1 次元の河床変動を考える場合の河床変動の連続式(11)式も，\(w_f \cdot c\) の代わりに \(w_f \cdot c_b\) とする必要がある。 したがって，浮遊砂による河床変動の連統式は次式で与えられることになる。

(29)\[ \frac{dz}{dt} = -\frac{1}{1 - \lambda} \left( q_{su} - w_f \frac{\beta}{1 - e^{-\beta}} c \right) \]

 以上で， 浮遊砂によるI 次元の河床変動計算を行う準備が整ったので， ここでは河床変動の基礎式を差分法により解く手順を示す。 図-4.7 は浮遊砂による河床変動計算のフローである。

1. 現河床形について，与えられた流量条件のもとに不等流計算を行い，掃流力の縦断分布を求める。

2. 砂粒の浮上量式を用いて，浮上粒子量の縦断分布を求める。

3. 浮遊砂濃度の連続式により，浮遊砂濃度の縦断分布を求める。

4. 河床変動の連統式により，河床変動量を求める。

 以上のプロセスを繰り返し行うことにより， 河床高の時間変化を予測することができる。
 差分法により安定な数値解を得るためには， 差分スキームの与え方，差分幅 \(\Delta x\)，\(\Delta t\) のとり方， 境界条件の設定に注意が必要である。これらの点については，以下の 演習問題をとおして解説することにする。

図-4.7　浮遊砂による河床変動計算のフ口ー

演習問題 16

 砂粒の粒径 \(d\) = 0.05, 0.1, 1 mm の場合について， おのおの無次元掃流力 \(\tau_*\) = 0.1, 1, 2, 5, 10 の場合の砂粒の浮上量 \(q_{su}\) を(4)式および(6)式で計算し，計算結果を比較せよ。

解答例

演習問題 17

 前出の演習問題 3で示した河川において， 河床砂の粒径 \(d\) = 0.1 mm とした場合について，以下の設問に答えよ。

1. 砂粒の沈降速度 \(w_f\) を Rubey の式により求めよ。

2. 流量 \(Q\) = 4000 m³/s，下流端水位 \(H\) = 5 m のとき，水面形を求めよ。ただし，Manning の粗度係数 \(n\) = 0.025 とする。

3. 各断面の摩擦速度 \(u_*\) および無次元掃流力 \(\tau_*\) を求めよ。

4. 各断面における砂粒の流砂形態を判定せよ。

5. 各断面の砂粒の浮上量 \(q_{su}\) を板倉の式(4)式，あるいは(6)式により求めよ。

6. 各断面の浮遊砂濃度 \(c\) を(10)式 (後進差分) により求めよ。ただし，境界条件として与える \(c\) は(9)式の右辺 = 0 として得られる \(c = q_{su} / w_f\) とする。

7. 6. で得られた \(c\) と各断面で \(c = q_{su} / w_f\) として計算した \(c\) を比較せよ。

解答例

演習問題 18

 河床勾配 \(i_b\) = 1/700，河幅 \(B\) = 100 m, Manningの粗度係数 \(n\) = 0.02，河床砂の粒径 \(d\) = 0.1 mm の広矩形断面水路に流量 \(Q\) = 500 m³/s が流下する場合について， 以下の設問に答えよ。 ただし，下流端の水位 \(H\) = 12 m， 同河床高 \(Z\) = 0 m (標高) とし，計算延長 \(L\) = 10 km， 計算区間距離 \(\Delta x\) = 200 m とする。

1. 初期断面における水面形を求めよ。

2. 各断面の浮遊砂濃度 \(c\) を(10)式で求めよ。ただし，差分計算は後進差分で行い，上流端の濃度 \(c_0 = q_{su} / w_f\) とせよ。

3. (11)式を用いて，各断面の 10 秒後の河床変動高 \(\Delta z\) を後進差分で求めよ。ただし，境界条件として上流端の \(z\) = 0 を与えよ。

4. 計算時間間隔 \(\Delta t\) = 10 秒として，24 時間分の河床変動の過程を縦断図に示せ。なお，縦断図には 1, 4, 12, 24 時間後の河床形状を描くこと。

解答例

演習問題 19

 演習問題 18の条件で， 浮遊砂濃度 \(c\) の計算を(13)式で行った場合の河床変動を計算せよ。

解答例

演習問題 20

 前出の演習問題 18の条件で， 下記の 3 ケースについて河床変動計算を行ったときの計算法，差分法，プログラムおよび計算結果を示せ。 ただし，拡散係数 \(D\) は 0.001 とする。

1. 浮遊砂の濃度 \(c\) の計算を(26)式，河床変動高の算定を(29)式で行った場合

2. 浮遊砂の濃度 \(c\) の計算を(27)式，河床変動高の算定を(29)式で行った場合

3. 浮遊砂の濃度 \(c\) の計算を(28)式，河床変動高の算定を(29)式で行った場合

解答例

---

参考文献

1) 板倉忠興：河川における乱流拡散現象に関する研究，土木試験所報告，第 83 号，昭和 59 年 7 月