演習問題

問題 1

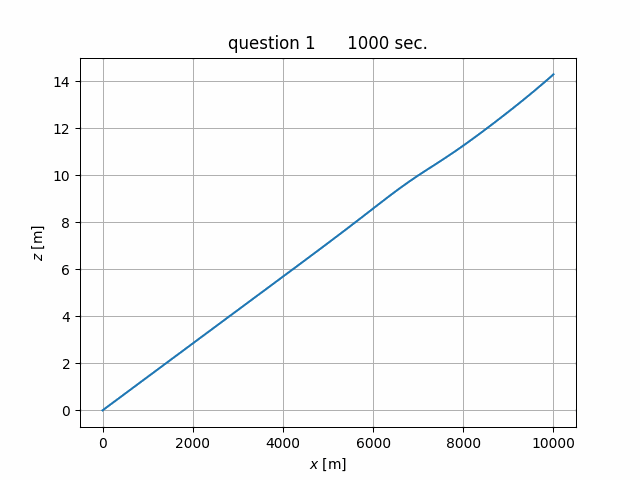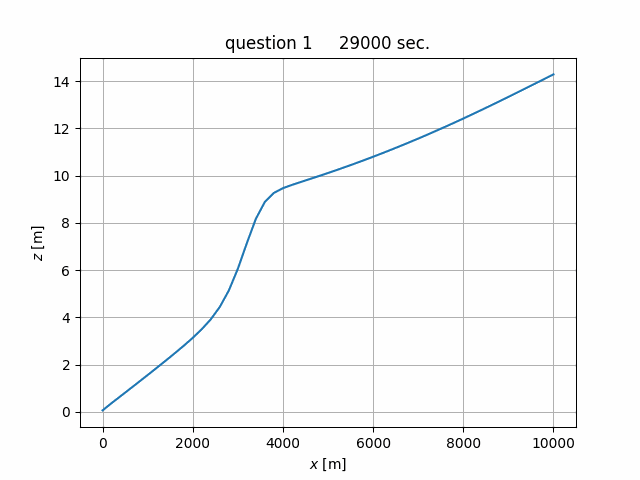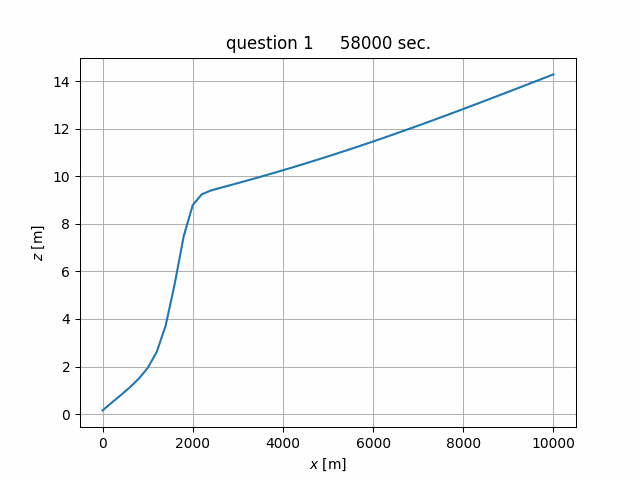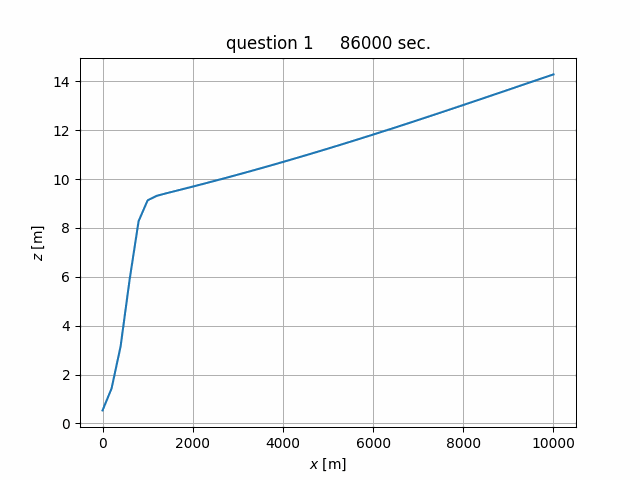
 粗度係数 \(n\) = 0.02，河床勾配 \(i_b\) ＝ 1/1,000， 河幅 \(B\) = 200 m の広矩形断面に， 流量 \(Q\) = 2,000 m3/s が常流で流下するときの水面形を求めよ。 ただし，下流端の水深を 5 m, 河床高を 0 m とし，\(\Delta x\) = 500 m のピッチで上流 5 km 地点まで計算すること。

解 答

(1) 考え方

 流れが常流であるので、式(2.27) の左辺（添字が 2 である下流の計算点の諸量）は既知量として扱うことができる。 すなわち，

(1)\[\begin{split} \begin{align*} f(h_1) &= z_1 + h_1 + \frac{q_1^2}{2 \mathrm{g} h_1^2} - \frac{n^2 q_1^2}{h_1^{10/3}} \frac{\Delta x}{2} - \mbox{const} \\&= h_1 + \frac{K_v}{h_1^2} - \frac{K_f}{h_1^{10/3}} - C = 0 \end{align*} \end{split}\]

である。 式中，\(q_1 = Q / B_1\) とおいた。また，\(K_v\)，\(K_f\)，\(C\) はそれぞれ

(2)\[ K_v = \frac{q_1^2}{2 \mathrm{g}} \,,\quad K_f = \frac{1}{2} n^2 q_1^2 \Delta x \,,\quad C = H_2 + \frac{q_2^2}{2 \mathrm{g}h_2^2} + \frac{1}{2} \frac{n^2 q_2^2 \Delta x}{h_2^{10/3}} - z_1 \]

である。 本問では，河幅および計算刻みが不変なので \(K_v\)，\(K_f\) は一定値である。
 式(1) の近似解はニュートン法（補遺 1）を適用して求めることができる。 すなわち，次の演算を繰り返すことで正解に漸近させることができる。

(3)\[ h_1 \leftarrow h_1 - f(h_1) / f'(h_1) \]

 関数 \(f\) の導関数 \(f'\) を具体的に計算すると，

(4)\[ f'(h_1) = 1 + \left( - \frac{2K_v}{h_1^2} + \frac{10}{3} \frac{K_f}{h_1^{10/3}} \right) \frac{1}{h_1} \]

である。
 以上を踏まえて，本問の計算流れは下記となる。

  1. 式(2) の \(K_v\)，\(K_f\) を求める

  2. 下流端の条件を適用して \(x = \Delta x\) の計算点の \(C\) を求める

  3. 下流の計算点の水深を \(h_1\) の初期値として 式(3) の演算を繰返して式(1) を解く

  4. \(x\) が上流端の \(x\) に等しい場合は計算終了

  5. \(x \leftarrow x + \Delta x\) として（1 つ上流の計算点に移って），その計算点の \(C\) を求める

  6. ステップ 3. に戻る

(2) プログラム

 上記の計算の流れを Python で記述したプログラムを excercise_1.py に示す。

(4) 計算結果


\(x\)
[m]

\(z\)
[m]

\(H\)
[m]

0

0.0

5.000

500

0.5

5.070

1000

1.0

5.169

1500

1.5

5.313

2000

2.0

5.518

2500

2.5

5.800

3000

3.0

6.160

3500

3.5

6.585

4000

4.0

7.050

4500

4.5

7.534

5000

5.0

8.028

問題 2

 粗度係数 \(n\) = 0.02, 河床勾配 \(i_b\) = 1/100， 河幅 \(B\) = 200 m の広矩形断面に， 流量 \(Q\) = 2,000 m3/s が射流で流下するときの水面形を求めよ。 ただし，上流端の水深を 1.4 m, 河床高を 50 m とし， \(\Delta x\) = 500 m と \(\Delta x\) = 100 m の 2 とおりのピッチで下流 5 km 地点まで計算すること。

解 答

(1) 考え方

 演習問題 1 との相違は流れが射流であることにある。 この場合は，式(2.27) の右辺（添字が 1 である上流の計算点の諸量）を既知量として扱うことができるから， 演習 1 で示した諸式を次のように差替えれば良い。 元の式と比較すると \(z\) と \(h\) の添字および \(K_f\) に係る符号が反転しているだけであることが分かる。

(5)\[\begin{split} \begin{align*}& f(h_2) = h_2 + \frac{K_v}{h_2^2} + \frac{K_f}{h_2^{10/3}} - C = 0 \\& C = H_1 + \frac{K_v}{h_1^2} - \frac{K_f}{h_1^{10/3}} - z_2 \\& h_2 \leftarrow h_2 - f(h_2) / f'(h_2) \\& f'(h_2) = 1 + \left( - \frac{2K_v}{h_2^2} - \frac{10}{3} \frac{K_f}{h_2^{10/3}} \right) \frac{1}{h_2} \end{align*} \end{split}\]

 計算の流れも上流端から計算を開始することを除いて， 演習 1 と同様である。

(2) プログラム

 本問の計算プログラムを excercise_2.py に示す。 二通りの \(\Delta x\) で計算するためにサブルーチン化しているものの， dx に負の値を与えただけで， ほぼ excercise_1.py を流用している。

(3) 計算結果

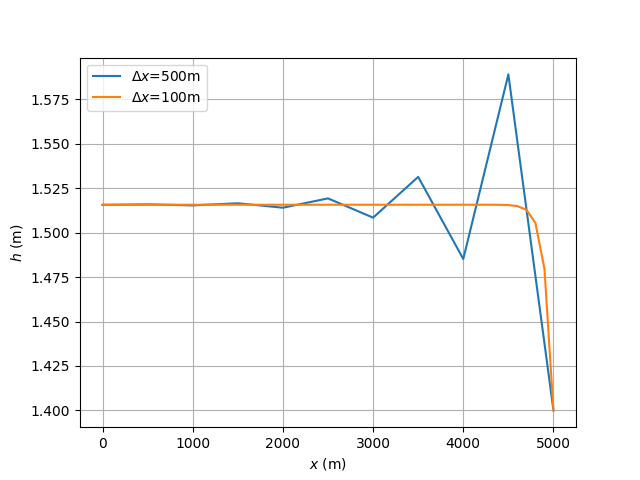
 水位の縦断分布では \(\Delta x\) の多少による違いが不明瞭なので水深の縦断分布を図示する。 \(\Delta x\) = 500 m のケースでは解が不自然に振動している。 射流の場合は適切な計算刻みで計算を実行しないと， このような不合理な結果となる。


\(x\) [m]

\(z\) [m]

\(\Delta x\) = 500 [m]
\(h\) [m]

\(\Delta x\) = 100 [m]
\(h\) [m]

5000

50.0

1.400

1.400

4900

49.0

1.480

4800

48.0

1.505

4700

47.0

1.513

4600

46.0

1.515

4500

45.0

1.589

1.515

4400

44.0

1.516

4000

40.0

1.485

1.516

3500

35.0

1.531

1.516

3000

30.0

1.508

1.516

2500

25.0

1.519

1.516

2000

20.0

1.514

1.516

1500

15.0

1.517

1.516

1000

10.0

1.515

1.516

500

5.0

1.516

1.516

0

0.0

1.516

1.516

問題 3

 河床高および川幅が下表に示されるような広矩形断面河川に， 流量 \(Q\) = 1,500 m3/s が流下した場合の水面形を求めよ。 ただし，粗度係数 \(n\) = 0.025，下流端の水深を 2.5 m とする。

断面番号

下流端から
の距離 (m)

河床高
\(z\) (m)

河 幅
\(B\) (m)

1

0

0

300

2

500

0.5

320

3

1000

0.9

280

4

1200

0.8

250

5

1800

2.0

300

6

2100

2.3

300

7

2500

3.0

320

8

3000

3.0

350

9

3300

3.5

300

10

3800

4.0

250

解 答

(1) 考え方

 考え方は演習問題 1 と同じである。 ただし，計算点の間隔が一定ではないので，式(1) の \(\Delta x\) はこれを反映して，

(6)\[ \Delta x = x_2 - x_1 \]

とする必要がある。

(2) プログラム

 本問に対する計算プログラムを excercise_3.py に示す。 河床勾配・川幅が変化に対応する部分が演習問題 1 とは異なる。
 なお，本問の計算結果は後出の演習問題でも用いることとなるので， 水位以外の水理量も出力することとした。

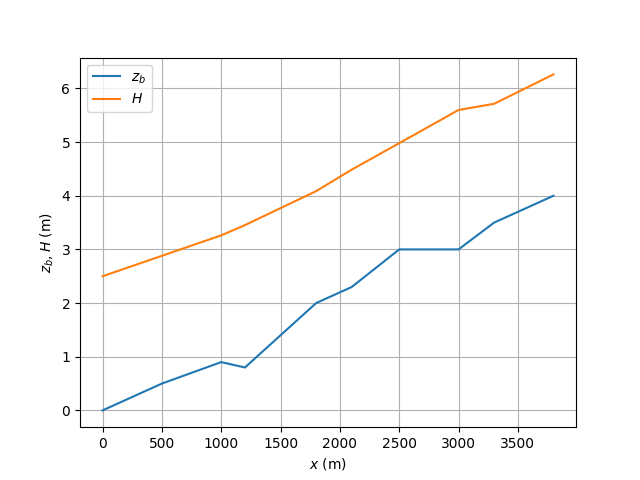
(3) 計算結果


\(x\)
[m]

\(z\)
[m]

\(H\)
[m]

\(h\)
[m]

\(1/S_f\)

0

0.0

2.500

2.500

1357

500

0.5

2.881

2.381

1313

1000

0.9

3.262

2.362

979

1200

0.8

3.453

2.653

1149

1800

2.0

4.086

2.086

742

2100

2.3

4.487

2.187

869

2500

3.0

4.980

1.980

709

3000

3.0

5.598

2.598

2101

3300

3.5

5.714

2.214

905

3800

4.0

6.262

2.262

675

問題 4

 下図に示すような複断面河川において， 流量 \(Q\) = 1,500 m3/s が流下した場合の水面形および分担流量を求めよ。 ただし，低水路幅，河床高および計算断面の断面間隔は前出の演習問題 3 と同一とする。 また，下流端の低水路の水深は 1.5 m とする。


解 答

(1) 考え方

 与えられた計算断面は左右対称なので， 低水路・高水敷 (左右岸を合わせて 1 ブロック) の 2 ブロックで構成される。 それぞれの諸量に添え字 \(l\)，\(h\) を付して区別すれば， 式 (2.33) より，

\[ \frac{u_l}{\sqrt{i_e}} = \frac{h_l^{2/3}}{n_l} \,,\quad \frac{u_h}{\sqrt{i_e}} = \frac{h_h^{2/3}}{n_h} \]

である。よって 式 (2.34) において \(\Delta q_l = (u_l h_l) B_l\)，\(\Delta q_h = (u_h h_h) B_h\) であるから，

\[ \frac{Q_l}{\sqrt{i_e}} = \frac{h_l^{5/3}}{n_l} B_l \,,\quad \frac{Q_h}{\sqrt{i_e}} = \frac{h_h^{5/3}}{n_h} B_h \]

である。したがって，式 (2.36) より，

\[ i_e = Q^2 \left[ \left( \frac{Q_l}{\sqrt{i_e}} \right)^{\!\!2} + \left( \frac{Q_h}{\sqrt{i_e}} \right)^{\!\!2} \right]^{\!-1} \]

である。さらに，低水路の流積を \(A_l (= B_l h_l)\)，高水敷の流積を \(A_h (= B_h h_h)\) とおいて，

\[\begin{split} \begin{align*} \frac{\alpha V^2}{2 \mathrm{g}} =& \frac{u_l^2 A_l + u_h^2 A_h}{2 \mathrm{g} \bigl( A_l + A_h \bigr)} = \frac{(u_l^2 h_l) B_l + (u_h^2 h_u) B_h}{2 \mathrm{g} A} \\ =& \frac{i_e}{2 \mathrm{g} A} \left( \frac{h_l^{7/3}}{n_l^2} B_l + \frac{h_h^{7/3}}{n_h^2} B_h \right) = \frac{i_e}{2 \mathrm{g} A} \left[ \left( \frac{Q_l}{\sqrt{i_e}} \right)^{\!\!2} \frac{1}{A_l} + \left( \frac{Q_h}{\sqrt{i_e}} \right)^{\!\!2} \frac{1}{A_h} \right] \end{align*} \end{split}\]

である。 上式を \(V^2 / 2 \mathrm{g} \,(= Q^2 / 2 \mathrm{g} A^2)\) で除して求められるエネルギー補正係数 \(\alpha\) は式 (2.38) と等価である。
 流れが常流なので， 式 (2.40) における左辺の下流側の計算点の諸量を既知として，

\[ f(H_1) = H_1 + \frac{\alpha V_1^2}{2 \mathrm{g}} - \frac{\Delta x}{2} i_{e1} - \mbox{const} = 0 \]

を解く。 ニュートン法によってこれを解く際に用いる導関数 \(f'(H_1)\) は， (4)式にならって下式で与える。 本式は正確ではないが，解を収束させるうえで差し支えない。

\[ f'(H_1) = 1 + \left( -\frac{\alpha V_1^2}{\mathrm{g}} + \frac{10}{3} \frac{\Delta x}{2} i_{e1} \right)\frac{1}{h_{l1}} \]

(2) プログラム

 本問の計算プログラムを excercise_4.py に示す。
 上記の速度水頭 \(\alpha V^2 / 2 \mathrm{g}\) およびエネルギー勾配 \(i_e\) の計算は conpound 関数で計算している。 この点を除いて，基本的な構造は演習問題 3で使用したプログラムを流用している。

(3) 計算結果


\(x\)
[m]

\(z\)
[m]

\(H\)
[m]

\(Q_l\)
[m3/s]

0

0.0

2.500

1265

500

0.5

2.889

1299

1000

0.9

3.310

1270

1200

0.8

3.508

1183

1800

2.0

4.104

1355

2100

2.3

4.551

1319

2500

3.0

5.053

1376

3000

3.0

5.673

1265

3300

3.5

5.812

1305

3800

4.0

6.356

1260

問題 5

  1. 岩垣の式 (3.7) により，粒径 \(d\) = 5 mm，1 mm， 0.1 mm のときの限界摩擦速度 \(u_{*c}\) および無次元限界掃流カ \(\tau_{*c}\) を求めよ。

  2. 粒径 \(d\) > 0.303 cm の場合の \(\tau_{*c}\) を求めよ。

解 答

  1. 下表の通り． なお，式 (3.7) を適用するから砂粒の水中比重 \(s\) は 1.65 である．

①

②

③

④

⑤

⑥

\(d\)
(cm)

\(u_{*c}^2\) の
算定式

\(u_{*c}^2\)
(cm2/s2)

\(u_{*c}\)
(cm/s)

\(s\mathrm{g}d\)
(cm2/s2)

\(\tau_{*c}\)
③÷⑤

0.5

\(80.9 d\)

40.45

6.360

808.5

0.050

0.1

\(55 d\)

5.5

2.345

161.7

0.034

0.01

\(8.41 d^{11/32}\)

1.727

1.314

16.17

0.107

  1. 粒径 \(d\) > 0.303 cm に対して

\(\qquad\tau_{*c} = 80.9 d / sgd = 80.9 / sg = 80.9 \div (1.65 \times 980) = 0.05\)

である。

問題 6

 河幅 \(B\) = 200 m，河床勾配 \(i_b\) = 1 / 1000 の広矩形断面水路を流量 \(Q\) = 500 m3/s が等流状態で流下している場合について以下の設間に答えよ。 ただし，Manning の粗度係数 \(n\) = 0.02 とする。

  1. 等流水深 \(h_0\) を求めよ。

  2. 掃流力 \(\tau_0\) を求めよ。

  3. 摩擦速度 \(u_*\) を求めよ。

  4. 河床砂の粒径 \(d\) = 1 cm としたときの無次元掃流力 \(\tau_*\)， 限界摩擦速度 \(u_{*c}\)，無次元限界掃流力 \(\tau_{*c}\) を求めよ。ただし，粒子の水中比重 \(s\) = 1.65 とする。

  5. 上記の水理条件で，粒径 \(d\) = 1 cm の河床砂が移動するかどうか判定せよ。

  6. 上記の水理条件で河床砂が移動しないようにするためには． 粒径 \(d\) をなん cm 以上とするとよいか。

  7. 粒径 \(d\) = 1 cm の河床砂が移動しないためには，流量 \(Q\) はなん m3/s 以下とするとよいか。

解 答

 設問 1 - 5 については以下の諸式を使用する．

\[\begin{split} \begin{align*}& h_0 = \left( \frac{n Q}{B \sqrt{i_e}} \right)^{\!\!3/5} \!\!,\quad \tau_0 = \rho \mathrm{g} h i_e \,,\quad u_* = \sqrt{\frac{\tau_0}{\rho}} \,,\quad \tau_* = \frac{u_*^2}{s\mathrm{g}d} \\& \tau_{*c} = 0.05 \,\,(d > 0.303\,\mbox{cm}) \,,\quad u_{*c} = \sqrt{\tau_{*c}\cdot s\mathrm{g}d} \\& d\bigr|_{\tau_*=\tau_{*c}} \!\!= \frac{u_{*}^2}{s\mathrm{g} \tau_{*c}} \,,\quad h\bigr|_{\tau_*=\tau_{*c}} \!\!= \frac{u_{*c}^2}{\mathrm{g} i_e} \end{align*} \end{split}\]

 上式を摘要して

\(\qquad h_0 = \bigl[ 0.02 \times 500 \div (200 \times \sqrt{1/1000}) \bigr]^{3/5} = 1.316\) [m]
\(\qquad \tau_0 = 1000 \times 9.8 \times 1.316 \times 1/1000 = 12.90\) [N/m2]
\(\qquad u_* = \sqrt{12.9 \div 1000} = 0.1136\) [m/s] \(= 11.36\) [cm/s
\(\qquad \tau_* = 11.36^2 \div (1.65 \times 980 \times 1) = 11.36^2 \div 1617 = 0.0798\)
\(\qquad u_{*c}=\sqrt{0.05\times 1617} = 8.99\) [cm/s]
\(\qquad \tau_* > \tau_{*c}=0.05\) であるから河床砂は移動する．

 \(\tau_* = \tau_{*c}\) となる時の粒径（移動限界粒径）を \(d_{*c}\) とおくと \(\tau_{*c} = u_*^2 / s\mathrm{g}d_{*c}\) であるから

(7)\[ d_{*c} = \frac{u_*^2}{s\mathrm{g}\tau_{*c}} \]

である．ここでは \(d_{*c} = 11.36^2 \div (1.65 \times 980 \times 0.05) = 1.596\) [cm] である．この粒径以上の河床砂は移動しない．
 また \(u_*=u_{*c}\) となる時の水深を \(h_{*c}\) とおくと \(u^2_{*c} = \mathrm{g}h_{*c}i_e\) であるから \(h_{*c} = u^2_{*c}/\mathrm{g}i_e\)． ここでは \(h_{*c} = 8.99^2 \div (980 \times 1/1000) = 82.5\) [cm] であり，この時の流量は
\(\qquad B h_*^{5/3} \sqrt{i_e} / n = 200 \times 0.825^{5/3} \times \sqrt{1/1000} \div 0.02 = 229.5\) [m3/s]
 これ以下の流量では河床砂は移動しない．

問題 7

 前出の演習問題 3で求めた流れのもとで， 各断面の河床砂が移動しないためには， 各断面の粒径 \(d\) をなん cm にするとよいか。

解 答

  移動限界粒径 \(d_{*c}\) は 式(7) で計算されるが， 特に粒径が 0.303 cm を超える場合 \(\tau_{*c}=0.05\) で \(s\mathrm{g}\tau_{*c}=1.65 \times 980 \times 0.05 = 80.85\) [cm/s2] となるから \(d_{*c} = u_*^2/80.85\) で計算される．
 下表はこれを踏まえて各計算点で移動しない河床砂の粒径を求めたものである． 表中 ② および ③ は 演習問題 3 の結果を引用した．

①

②

③

④
=980×②÷③

⑤
=④÷80.85

\(x\)
[cm]

\(h\)
[cm]

\(1/i_e\)

\(u_*^2\)
[cm2/s2]

\(d\)
[cm]

0

2500

1357

180.5

2.23

500

2381

1313

177.7

2.20

1000

2362

979

236.4

2.93

1200

2653

1149

226.3

2.79

1800

2086

742

275.5

3.41

2100

2187

869

246.6

3.06

2500

1980

709

273.7

3.39

3000

2598

2101

121.2

1.50

3300

2214

905

239.7

2.97

3800

2262

675

328.4

4.05

問題 8

 粒径 \(d\) = 1 mm の砂の沈降速度 \(w_f\) を求め， 摩擦速度 \(u_*\) = 20 cm/s のとき浮遊・掃流形式のいずれとなるか判定せよ。

解 答

 式 (3.11) の両辺に \(\sqrt{s\mathrm{g}d}\) を乗じて， 沈降速度は次式となる．

(8)\[ w_f = \sqrt{\frac{2}{3} s\mathrm{g}d + \left( \frac{6\nu}{d} \right)^2 } - \frac{6\nu}{d} \]

 砂の水中比重 \(s\) を 1.65，水の動粘性係数 \(\nu\) を 0.01 [cm2/s] として，粒径 0.1 cm の粒子では \(s\mathrm{g}d=1.65 \times 980 \times 0.1 = 161.7\) [cm2/s2]， \(6\nu/d = 6 \times 0.01 \div 0.1 = 0.6\) [cm/s] より

\( \qquad w_f = \sqrt{2 \times 161.7 \div 3 + 0.6^2} - 0.6 = 9.8 \) [cm/s]

 \(u_*\) = 20 cm/s の時 \(u_* / w_f=20 \div 9.8 = 2.04\) となり， 式 (3.10) より \(u_* / w_f > 1.67\) であるから浮遊形式での移動が卓越する．

問題 9

 河幅 \(B\) =200 m，河床勾配 \(i_b\) ＝ 1/1000, Manning の粗度係数 \(n\) = 0.02 なる広矩形断面水路に流量 \(Q\) = 500 m3/s が等流状態で流れているとき， 粒径 \(d\) = 1 mm の砂は浮遊・掃流形式のいずれとなるか判定せよ。

解 答

 演習問題 6 より \(u_* = 11.36\) [cm/s]， 演習問題 8 より \(w_f = 9.8\) [cm/s] であるから， \(u_* / w_f=11.36 \div 9.8 = 1.16\) で 式 (3.10) より \(1.08 < u_* / w_f < 1.67\) であるから掃流・浮遊が混在する形式で移動する．

問題 10

 粒径 \(d\) = 1 mm の砂について，以下の設間に答えよ。

  1. 無次元掃流力 \(\tau_*\) = 0.3 のときの砂の移動形式は，浮遊・掃流のいずれとなるか判定せよ。

  2. 無次元掃流力 \(\tau_*\) をどの程度まで上げると，浮遊砂が卓越する領域に入るか判定せよ。

解 答

 同じく粒径 0.01 cm の粒子について検討した 演習問題 8 の解答より \(w_f = 9.8\) [cm/s]． また \(u_*^2 > (1.67 w_f)^2\) の時に浮遊砂が卓越する．

  1. \(u_* = \sqrt{\tau_* s \mathrm{g} d} = \sqrt{0.3 \times 1.65 \times 980 \times 0.01} = 7.0\) [cm/s] であるから， \(u_* / w_f=7.0 \div 9.8 = 0.71\) で 式 (3.10) より \(u_* / w_f < 1.08\) より掃流形式で移動する．

  2. \(\tau_* > (1.67 w_f)^2 / s \mathrm{g} d = (1.67 \times 9.8)^2 \div (1.65 \times 980 \times 0.1) = 1.66\) であれば浮遊砂が卓越する．

問題 11

 摩擦速度 \(u_*\) = 20 cm/s，粒径 \(d\) = 5 mm，\(n\) ＝ 0.03 のとき， 土研公式 (3.13) および Meyer-Peter・Müller 式 (3.15) により単位幅当たりの掃流砂量 \(q_B\) を求めよ。

解 答

 粒径が 0.303 [cm] を超えるから無次元限界掃流カ \(\tau_{*c}\) は 0.05 で

\(\qquad s\mathrm{g} = 1.65 \times 980 = 1617\) [cm/s2]， \(s\mathrm{g}d = 1617 \times 0.5 = 808.5\) [cm2/s2]

土研公式

 \(n \ge\) 0.025 の時，\(f\) = 0.623 であるから，

\(\qquad u_{*c}^2 = \tau_{*c} s \mathrm{g} d = 0.05 \times 808.5 = 40.43\) [cm2/s2]
\(\qquad F = \bigl[ 1 + 8 \bigl( u_{*c}^2 / u_*^2 \bigr)^4 \bigr]^{-1} = \bigl[ 1 + 8 \times \bigl( 40.43 / 20^2 \bigr)^4 \bigr]^{-1} = 0.999\)
\(\qquad q_B = u_*^3 F f / s \mathrm{g} = 20^3 \times 0.999 \times 0.623 \div 1617 = 3.08\) [cm3/s/cm]

Meyer-Peter・Müller 式

\(\qquad \tau_* = u_*^2 / s \mathrm{g} d = 20^2 \div 808.5 = 0.495\)
\(\qquad q_B = 8 \bigl( \tau_* - \tau_{*c} \bigr)^{1.5} \sqrt{ s \mathrm{g} d^3} = 8 \times \bigl( 0.495 - 0.05 \bigr)^{1.5} \times \sqrt{1617 \times 0.5^3} = 3.38\) [cm3/s/cm]

問題 12

 河幅 \(B\) = 300 m，河床勾配 \(i_b\) ＝ 1/500, Manning の粗度係数 \(n\) = 0.02 なる広矩形断面水路において， 流量 \(Q\) = 1000 m3/s が等流状態で流れている場合について， 以下の設問に答えよ。

  1. 粒径 \(d\) = 3 mm の砂の単位幅当たりの掃流砂量 \(q_B\) を，Meyer-Peter・Müller 式 (3.15) により求めよ。

  2. 断面内の全掃流砂量 \(Q_B\) を求めよ。

解 答

 等流水深および無次元掃流力は

\(\qquad h_0 = \bigl( n Q / B \sqrt{i_e}\bigr)^{3/5} =\bigl[ 0.02 \times 1000 \div \bigl(300 \times \sqrt{0.002}\bigr)\bigr]^{3/5} =1.271\) [m]
\(\qquad \tau_* = h_0 i_e / sd = 1271 \div \bigl( 500 \times 1.65 \times 3\bigr) = 0.514\)

 粒径 0.3 cm の時の無次元摩擦速度の二乗値 \(u_{*c}^2\) は岩垣の式 (3.7) より \(134.6 d^{31/22}\) であるから

\(\qquad u_{*c}^2 = 134.6 \times 0.3^{31/22}=24.675\) [cm2/s2]
\(\qquad \tau_* = u_{*c}^2 / s\mathrm{g}d = 24.675 \div \bigl( 1.65 \times 980 \times 0.3 \bigr)=0.051\)

 以上より，

\(\qquad q_B = 8 \bigl( \tau_* - \tau_{*c} \bigr)^{1.5} \sqrt{ s \mathrm{g} d^3} = 8 \times \bigl( 0.514 - 0.051 \bigr)^{1.5} \times \sqrt{1.65 \times 980 \times 0.3^3}\)
\(\hphantom{\qquad q_B}= 16.6\) [cm3/s/cm] \(= 1.66 \times 10^{-3}\) [m3/s/m]
\(\qquad Q_B = q_b B = 1.66 \times 10^{-3} \times 300 = 0.498\) [m3/s]

問題 13

 前出の演習問題 3で求めた流れにおいて， 河床砂の粒径を \(d\) = 1 cm としたとき， 各断面について以下の設問に答えよ。

  1. 河床砂が移動するかどうか判定せよ。

  2. 河床砂の移動形式を判定せよ。

  3. Meyer-Peter・Müller 式 (4.10) により \(q_B\) を求めよ。

  4. 全掃流砂量 \(Q_B\) を求めよ。

解 答

 式 (8) より， 河床砂の水中比重 \(s\) を 1.65 として \(s\mathrm{g}=1.65 \times 980 \times 1 = 1617\) [cm2/s]． また水の動粘性係数 \(\nu\) を 0.01 [cm2/s] として \(6 \nu / d = 0.06\) であるから

\( \qquad w_f = \sqrt{2 \times 1617 \div 3 + 0.06^2} - 0.06 = 32.773 \) [cm/s]

 式(3.9)より， 摩擦速度 \(u_*\) が沈降速度 \(w_f\) の 1.08 倍を超えると河床の粒子は浮遊する． したがって，ここでは摩擦速度が \(1.08 \times 32.773 = 35.4\) [cm/s] を超えると粒子が浮遊する．
 下表の ③ は 問題 7 の結果を引用した． Meyer-Peter・Müller 式中の無次元掃流力 \(\tau_{*c}\) は粒径が 0.303 [cm] を超えるから 0.05 を当てる．
 この表より何れの計算点でも \(\tau_* > 0.05\) かつ \(u_* < 35.4\) [cm/s] であるから， 全区間で河床砂は掃流形式で移動する．

①

②

③

④
=③0.5

⑤
=③÷1617

⑥
=Eq(4.10)

⑦
=10-4×②×⑥

\(x\)
[m]

\(B\)
[m]

\(u_*^2\)
[cm2/s2]

\(u_*\)
[cm/s]

\(\tau_*\)

\(q_B\)
[cm3/s/cm]

\(Q_B\)
[m3/s]

0

300

180.5

13.4

0.112

4.92

0.148

500

320

177.7

13.3

0.110

4.72

0.151

1000

280

236.4

15.4

0.146

9.60

0.269

1200

250

226.3

15.0

0.140

8.68

0.217

1800

300

275.5

16.6

0.170

13.44

0.403

2100

300

246.6

15.7

0.153

10.56

0.317

2500

320

273.7

16.5

0.169

13.25

0.424

3000

350

121.2

11.0

0.075

1.27

0.044

3300

300

239.7

15.5

0.148

9.91

0.297

3800

250

328.4

18.1

0.203

19.27

0.482

問題 14

 砂の場合について， その移動形式を判定するグラフを作成せよ。 ただし，グラフは両対数グラフとし， 縦軸に無次元掃流力 \(\tau_*\)，横軸に粒径 \(d\) をとるものとする。
 なお，グラフ中に無次元限界掃流力 \(\tau_{*c}\) と粒径 \(d\) の関係についても記入せよ。

解 答

 式 (3.9) より， 砂粒の浮遊限界は下式となる．

\[ \frac{\bigl( 1.08 w_f \bigr)^2}{s \mathrm{g} d} < \tau_* < \frac{\bigl( 1.67 w_f \bigr)^2}{s \mathrm{g} d} \]

 下図は粒径を 0.01 [cm] から 1 [cm] まで変化させて， 上式による浮遊限界の上下限値ならび岩垣の式 (3.7) による無次元移動限界掃流力 \(\tau_{*c}\,(=u_{*c}^2 / s \mathrm{g} d)\) を図示したものである． 沈降速度 \(w_f\) は水の動粘性係数 \(\nu\) を 0.01 [cm2/s] として 式 (13) で計算した．
 描画には excercise_14.py を用いている． このプログラムでは paticle.py で記述した Particle クラスをインポートして使用している．


問題 15

 全長 \(L\) = 3000 m， 河床勾配 \(i_b\) = 1/1000，河幅 \(B\) = 100 m， 河床砂の粒径 \(d\) = 5 mm， Manning の粗度係数 \(n\) = 0.02 の広矩形断面水路に， 下図のように高さ 50 cm のマウンド (同一の河床砂，同一粗度)がある場合について， 以下の設問に答えよ。ただし，下流端の河床高 \(z\) = 0 m (標高) とする。

  1. 流量 \(Q\) = 1000 m3/s が流下するとき，マウンド部分 以外の地点の等流水深 \(h_0\) を求めよ。

  2. 下流端水深が等流水深 \(h_0\) の場合の水面形を区間距離 \(\Delta x\) = 100 mとして各断面ごと不等流計算により求めよ。

  3. 各断面における無次元掃流力 \(\tau_*\)，掃流砂量 \(q_B\) を求めよ。ただし，\(q_B\) は Meyer-Peter・Müller式 (3.10) で求めるものとする。


  1. 各断面の 10 秒後の河床変動量 \(\Delta z\) を後進差分で求めよ。ただし，境界条件として上流端の \(\Delta z\) = 0 を与えよ。

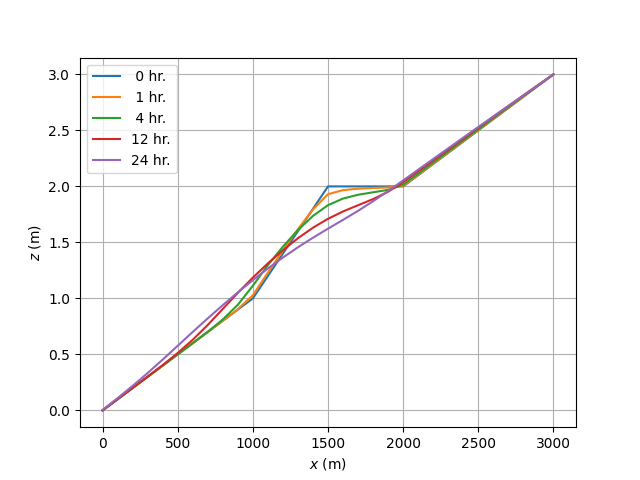
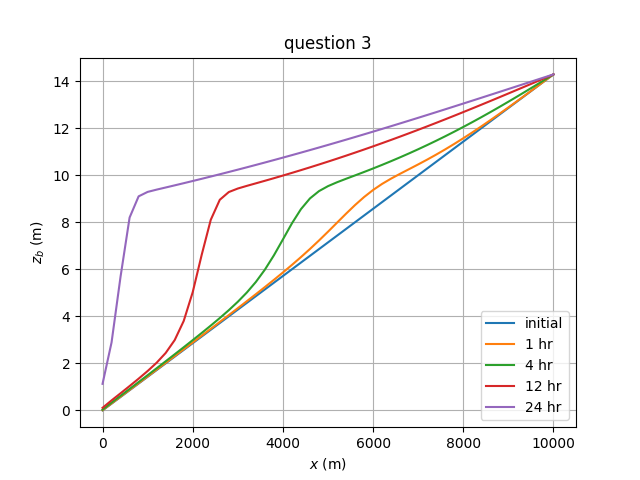
  2. 計算時間間隔 \(\Delta t\) = 10 秒として，24 時間分の河床変動計算を後進差分で行い，1，4，12，24 時間後の河床形状を縦断図にせよ。

解 答

(1) 考え方

 上流端で河床高の境界条件が与えられているので流れは常流と判断される。 したがって，河床高の変化は空隙率 \(\lambda\) を 0.4 として 式 (3.24) で計算する。
 河床砂の粒径が 0.303 [cm] を超えているので，Meyer-Peter・Müller式で用いる限界摩擦速度は 0.05 を当てる．
 水位計算は常流区間の広長断面水路に対する 演習問題 1 に準じて行う。 下流端の計算点におけるエネルギー勾配は 1/1,000 で固定する。

(2) プログラム

 本問の計算プログラムを excercise_15.py に示す。
 限界摩擦速度および無次元掃流量は Particle クラスのコンストラクタで計算している． また単位幅・単位時間当りの掃流砂量は同クラスの MPM メソッドで計算している。

(3) 計算結果

設問 1 - 4

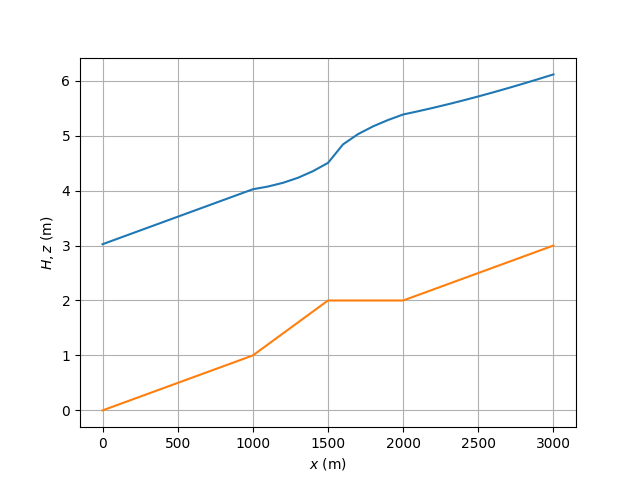
 初期河床に対する水面形は下図の通りである． また，各計算点での無次元掃流力，単位幅・単位時間当りの掃流砂量および 10 秒後の河床高の変化は下表の通りである． 下流端を含むマウンド部以外の等流水深は 3.024 m である．


\(x\)
[m]

\(z\)
[m]

\(H\)
[m]

\(\tau_*\)

\(q_b\)
[cm3/s/cm]

\(\Delta z\)
[μ]

0

0.0

3.024

0.367

20.256

0.000

100

0.1

3.124

0.367

20.256

0.000

200

0.2

3.224

0.367

20.256

0.000

300

0.3

3.324

0.367

20.256

0.000

400

0.4

3.424

0.367

20.256

0.000

500

0.5

3.524

0.367

20.256

0.000

600

0.6

3.624

0.367

20.256

0.000

700

0.7

3.724

0.367

20.256

0.000

800

0.8

3.824

0.367

20.256

0.000

900

0.9

3.924

0.367

20.256

0.000

1000

1.0

4.024

0.367

20.256

76.993

1100

1.2

4.073

0.413

24.876

85.057

1200

1.4

4.141

0.461

29.979

85.077

1300

1.6

4.233

0.507

35.084

73.194

1400

1.8

4.354

0.544

39.475

51.663

1500

2.0

4.504

0.569

42.575

-275.831

1600

2.0

4.841

0.424

26.025

-97.878

1700

2.0

5.028

0.365

20.152

-57.051

1800

2.0

5.169

0.329

16.729

-38.727

1900

2.0

5.285

0.302

14.406

-28.503

2000

2.0

5.385

0.282

12.696

11.177

2100

2.1

5.444

0.290

13.366

10.855

2200

2.2

5.506

0.298

14.017

10.429

2300

2.3

5.572

0.305

14.643

9.910

2400

2.4

5.641

0.312

15.238

9.276

2500

2.5

5.713

0.318

15.794

8.633

2600

2.6

5.788

0.324

16.312

7.953

2700

2.7

5.866

0.329

16.789

7.255

2800

2.8

5.947

0.334

17.225

6.558

2900

2.9

6.029

0.338

17.618

5.877

3000

3.0

6.114

0.342

17.971

0.000

  1，4，12，24 時間後の河床形状を下図に示す． マウンドは時間経過とともに高さを減じつつ下流に遷移している．


問題 16

 砂粒の粒径 \(d\) = 0.05, 0.1, 1 mm の場合について， おのおの無次元掃流力 \(\tau_*\) = 0.1, 1, 2, 5, 10 の場合の砂粒の浮上量 \(q_{su}\) を式 (4.4) および式 (4.6) で計算し，計算結果を比較せよ。

解 答

 本問の計算プログラムを excercise_16.py に示す． 浮上量は Particle クラス の Itakura メソッドで計算している． 同メソッドの第 2 引数は近似式を用いるか否かの選択肢で，これを False とした場合は 式 (4.4) を， これを True とした場合は 式 (4.6) を摘要する仕様とした． 既定は False である．
 演算に当って，式 (4.5) において，

\[ \frac{1}{\sqrt{\pi}}\int_{x}^{\infty} \xi \cdot e^{-\xi^2} \, d\xi = \frac{1}{\sqrt{\pi}}\left[ -\frac{e^{-\xi^2}}{2} \right]_{x}^{\infty} = \frac{1}{2 \sqrt{\pi}} e^{-x^2} \]

とする他，相補誤差関数

\[ \mbox{erfc}(x) = \frac{2}{\sqrt{\pi}} \int_x^{\infty} e^{-\xi^2} \,d\xi \]

の計算には python の組込関数 math.erfc(x) を用いた。
 結果は下表の通りである。上段は式 (4.4) ，下段は式 (4.6) による算定値である。

\(q_{su}\quad[\times 10^{-2}\mbox{cm}{}^3/\mbox{s}/\mbox{cm}{}^2]\)

\(d\) [mm]

\(\tau_*=0.1\)

\(\tau_*=1\)

\(\tau_*=2\)

\(\tau_*=5\)

\(\tau_*=10\)

0.05

0.0042
0.0012

1.390
1.396

2.122
2.125

3.537
3.536

5.114
5.108

0.1

0
0

1.546
1.555

2.581
2.585

4.583
4.580

6.812
6.804

1

0
0

0
0

2.447
2.459

8.776
8.768

15.82
15.80

問題 17

 演習問題 3 で示した河川において， 河床砂の粒径 \(d\) = 0.1 mm とした場合について，以下の設問に答えよ。

  1. 砂粒の沈降速度 \(w_f\) を Rubey の式により求めよ。

  2. 流量 \(Q\) = 4000 m3/s，下流端水位 \(H\) = 5 m のとき，水面形を求めよ。ただし，Manning の粗度係数 \(n\) = 0.025 とする。

  3. 各断面の摩擦速度 \(u_*\) および無次元掃流力 \(\tau_*\) を求めよ。

  4. 各断面における砂粒の流砂形態を判定せよ。

  5. 各断面の砂粒の浮上量 \(q_{su}\) を板倉の式 (4.4) あるいは式(4.6) により求めよ。

  6. 各断面の浮遊砂濃度 \(c\) を式(4.10) (後進差分) により求めよ。ただし，境界条件として与える \(c\) は式(4.9)の右辺 = 0 として得られる \(c = q_{su} / w_f\) とする。

    1. で得られた \(c\) と各断面で \(c = q_{su} / w_f\) として計算した \(c\) を比較せよ。

解 答

 excercise_17.py を用いて計算した結果を下表に示す。
 なお，粒径 0.1 mm の粒子の沈降速度 \(w_f\) は \(s\mathrm{g}d=1.65\times 980\times 0.01 = 16.17\) [cm/s]，\(36\nu^2/d^2=36\) より，

\(\qquad w_f = \sqrt{2 \times 16.17 \div 3 + 36} - 6 = 0.84\) [cm/s]

で，浮遊限界上限の無次元掃流量は

\(\quad(1.67 w_f)^2/s\mathrm{g}d=(1.67 \times 0.84)^2 \div 16.17 = 0.1216\)

であるから何れの計算点とも浮遊形式で移動する．

\(x\)
[m]

\(H\)
[m]

\(\tau_*\)

\(u_*\)
[cm/s]

\(q_{su}\)
[cm3/s/cm2]

\(c\)

\(q_{su}/w_f\)

0

5.00

15.752

15.960

0.087

0.124

0.104

500

5.28

15.405

15.783

0.086

0.130

0.103

1000

5.46

22.408

19.035

0.106

0.139

0.126

1200

5.55

25.529

20.318

0.113

0.141

0.135

1800

6.16

24.183

19.775

0.110

0.143

0.131

2100

6.45

24.378

19.854

0.111

0.145

0.132

2500

6.85

25.499

20.306

0.113

0.148

0.135

3000

7.47

15.070

15.610

0.085

0.153

0.102

3300

7.48

26.880

20.848

0.117

0.164

0.139

3800

7.90

40.538

25.603

0.145

0.172

0.172

問題 18

 河床勾配 \(i_b\) = 1/700，河幅 \(B\) = 100 m, Manningの粗度係数 \(n\) = 0.02，河床砂の粒径 \(d\) = 0.1 mm の広矩形断面水路に流量 \(Q\) = 500 m3/s が流下する場合について， 以下の設問に答えよ。 ただし，下流端の水位 \(H\) = 12 m， 同河床高 \(Z\) = 0 m (標高) とし，計算延長 \(L\) = 10 km， 計算区間距離 \(\Delta x\) = 200 m とする。

  1. 初期断面における水面形を求めよ。

  2. 各断面の浮遊砂濃度 \(c\) を式(4.10)で求めよ。ただし，差分計算は後進差分で行い，上流端の濃度 \(c_0 = q_{su} / w_f\) とせよ。

  3. 式(4.11)を用いて，各断面の 10 秒後の河床変動高 \(\Delta z\) を後進差分で求めよ。ただし，境界条件として上流端の \(z\) = 0 を与えよ。

  4. 計算時間間隔 \(\Delta t\) = 10 秒として，24 時間分の河床変動の過程を縦断図に示せ。なお，縦断図には 1, 4, 12, 24 時間後の河床形状を描くこと。

解 答

 excercise_18.py を用いた．
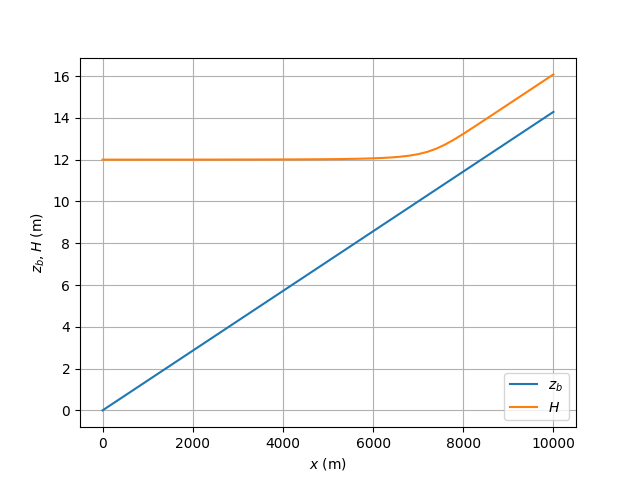
 初期河床に 500 m3/s が流下する時の水面形を下図に示す． 各計算点における浮遊砂濃度 \(c\) および 10 秒後の河床変動高は下表の通りである．


\(x\)
[m]

\(z_b\)
[m]

\(H\)
[m]

\(c\)
[%]

\(\Delta z\)
[μ]

0

0.000

12.000

0.1436

200.896

200

0.286

12.000

0.1918

231.479

400

0.571

12.000

0.2473

243.999

600

0.857

12.000

0.3059

257.575

800

1.143

12.001

0.3677

272.359

1000

1.429

12.001

0.4331

288.525

1200

1.714

12.001

0.5023

306.274

1400

2.000

12.001

0.5758

325.837

1600

2.286

12.001

0.6540

347.482

1800

2.571

12.002

0.7374

371.519

2000

2.857

12.002

0.8266

398.306

2200

3.143

12.002

0.9222

428.257

2400

3.429

12.003

1.0250

461.854

2600

3.714

12.003

1.1358

499.650

2800

4.000

12.004

1.2557

542.285

3000

4.286

12.004

1.3859

590.492

3200

4.571

12.005

1.5276

645.105

3400

4.857

12.006

1.6824

707.070

3600

5.143

12.007

1.8521

777.377

3800

5.429

12.008

2.0387

857.206

4000

5.714

12.009

2.2444

947.781

4200

6.000

12.011

2.4719

1050.358

4400

6.286

12.013

2.7240

1166.154

4600

6.571

12.015

3.0038

1296.213

4800

6.857

12.018

3.3149

1441.215

5000

7.143

12.022

3.6608

1601.160

5200

7.429

12.026

4.0451

1774.920

5400

7.714

12.032

4.4711

1959.568

5600

8.000

12.039

4.9414

2149.443

5800

8.286

12.049

5.4573

2334.877

6000

8.571

12.062

6.0176

2500.583

6200

8.857

12.080

6.6178

2623.875

6400

9.143

12.104

7.2475

2673.371

6600

9.429

12.139

7.8891

2609.934

6800

9.714

12.189

8.5155

2393.761

7000

10.000

12.263

9.0900

2003.936

7200

10.286

12.370

9.5709

1472.923

7400

10.571

12.523

9.9244

911.872

7600

10.857

12.725

10.1433

465.352

7800

11.143

12.966

10.2550

200.516

8000

11.429

13.233

10.3031

77.644

8200

11.714

13.511

10.3217

28.403

8400

12.000

13.794

10.3285

10.058

8600

12.286

14.079

10.3310

3.393

8800

12.571

14.364

10.3318

0.952

9000

12.857

14.650

10.3320

-0.000

9200

13.143

14.936

10.3320

-0.000

9400

13.429

15.221

10.3320

-0.000

9600

13.714

15.507

10.3320

-0.000

9800

14.000

15.793

10.3320

-0.000

10000

14.286

16.079

10.3320

0.000

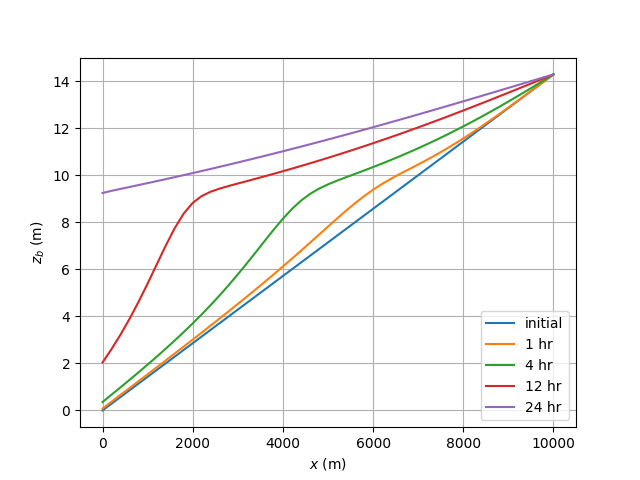
 1, 4, 12, 24 時間後の河床形状は下図のように計算される．


問題 19

 演習問題 18の条件で， 浮遊砂濃度 \(c\) の計算を式(4.13) で行った場合の河床変動を計算せよ。

解 答

 計算プログラムを excercise_19.py に示す．
 初期の浮遊砂濃度は全区間ゼロを仮定した． 1, 4, 12, 24 時間後の河床形状は下図の通りである．  演習問題 18 の結果に比べて濃度の伝播に時間を要するため，デルタの形成が遅くなっている．


問題 20

 前出の演習問題 18の条件で， 下記の 3 ケースについて河床変動計算を行ったときの計算法，差分法，プログラムおよび計算結果を示せ。 ただし，拡散係数 \(D\) は 0.001 とする。

  1. 浮遊砂の濃度 \(c\) の計算を式(4.26)，河床変動高の算定を式(4.29) で行った場合

  2. 浮遊砂の濃度 \(c\) の計算を式(4.27)，河床変動高の算定を式(4.29) で行った場合

  3. 浮遊砂の濃度 \(c\) の計算を式(4.28) ，河床変動高の算定を式(4.29) で行った場合

解 答

 式 (4.26) の離散化方程式は単位幅流量を \(q\) とおいて下式で与えられる．

\[\begin{split} \begin{align*}& \frac{c_i^{j+1} - c_i^j}{\Delta t} = D \left( \frac{c_{i+1}^j - 2 c_i^j + c_{i-1}^j}{\Delta x^2} \right) + \frac{1}{h_i} \left[ \bigl( q_{su} \bigr)_i^j - \frac{q_i c_i^j - q_{i-1} c_{i-1}^j}{\Delta x} - w_f \alpha_i c_i^j \right] \\& \alpha_i = \frac{(c_b)_i^j}{c_i^j} = \frac{\beta_i}{1 - \exp (-\beta_i)} \,,\quad \beta_i = \frac{6 w_f}{\kappa (u_*)_i} \end{align*} \end{split}\]

 添え字 \(i\)，\(j\) はそれぞれ空間格子，時間格子の番号である． \(i=0\) は上流端を指す．
 式(4.27) の離散化方程式は上式の右辺第 1 項を無視する． 式 (4.28) の離散化方程式はさらに左辺もゼロとして，

\[ \bigl( q_{su} \bigr)_i^j - \frac{q_i c_i^j - q_{i-1}c_{i-1}^j}{\Delta x} - w_f \alpha_i c_i^j = 0 \]

である． 式(4.29) の離散化方程式は何れのケースでも下式となる．

\[ \frac{z_i^{j+1} - z_i^j}{\Delta t} = -\frac{1}{1 - \lambda} \bigl[ \bigl( q_{su} \bigr)_i^j - w_f \alpha_i c_i^j\bigr] \]

 計算の実行に当っては以下の条件を付与した．

  • 何れのケースとも上流端では河床高の時間変化をゼロと仮定する．つまり上流端の濃度は \(c_0^j = \bigl( q_{su} \bigr)_0^j / w_f \alpha_0\) で与える．

  • 設問 1 および設問 2 において上流端以外の初期濃度はゼロを仮定する．

  • 設問 1 における下流端の拡散項はゼロとする．

  • カルマン定数 \(\kappa\) は 0.4 とする．

 以上を踏まえて 図―4.7 の流れを実装した計算プログラムを excercise_20.py に示す． 基準点濃度と鉛直平均濃度の比 \(\alpha\) は Particle クラスの cb_c メソッドで計算する仕様とした．
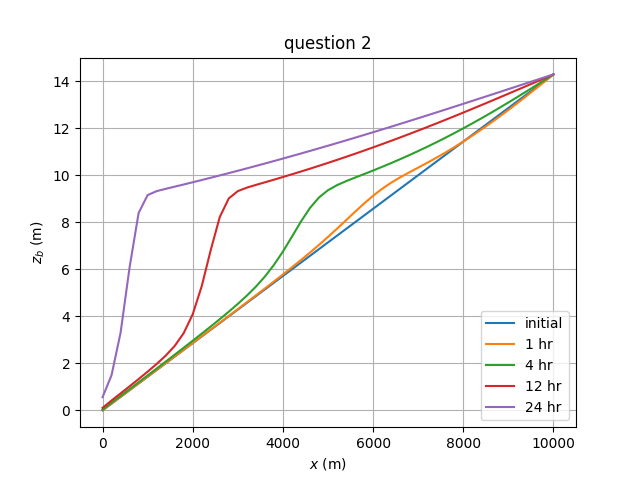
 設問別の 1, 4, 12, 24 時間後の河床形状は下図の通りである． \(\alpha\) は 1 より小さいので 問題 19 より河床からの供給量より小さくなるため， 同問の河床形状に比べてデルタの進行が遅くなる． question 1 と question 2 の違いは不分明であり， この条件下では浮遊砂濃度の拡散項の寄与が小さい事を示唆している．





問題 21

 河口からの距離およ川幅が下表に示されるような河川において， 流量 1,000 m3/s が 48 時間流下した場合の河床変動量を求めよ。
 ただし，河口水位を 0 m (一定)， 河床材料の粒径 \(d\) = 2 cm， 粗度係数 \(n\) = 0.025， 流砂は掃流砂のみとし， 流砂量式は \(q_b / \sqrt{s g d^3} = 8 (\tau_* - \tau_{*c})^{1.5}\) を用いること。また，断面は矩形とする。

  1. 上流端での流砂量は，動的平衡状態である（すなわち，上流端の河床変動はないとして計算せよ。

  2. 上流端にダムがあるとしで計算せよ (ダム地点では流砂量 ＝ 0)。

  3. 上記 1. において，K.P.2.6 地点に床止めがある場合の計算をせよ。

  4. 上記 1. において，K.P.2.2, 2.6, 3.0 に床止めがある場合の計算をせよ。

河道条件 [m]

\(x\)

\(B\)

\(z\)

\(x\)

\(B\)

\(z\)

0.0

300

-2.0

2.4

220

2.8

0.2

300

-1.6

2.6

220

3.2

0.4

300

-1.2

2.8

220

3.6

0.6

300

-0.8

3.0

220

4.0

0.8

300

-0.4

3.2

220

4.4

1.0

300

0.0

3.4

300

4.8

1.2

300

0.4

3.6

300

5.2

1.4

300

0.8

3.8

300

5.6

1.6

300

1.2

4.0

300

6.0

1.8

300

1.6

4.2

300

6.4

2.0

300

2.0

4.4

300

6.8

2.2

220

2.4

解 答

(1) 考え方

 基本的な河床変動計算は 問題 15 と同様である。河幅が変化するため、不等流計算では 問題 3 での不等流計算法を参考に設定する。
 本問の例は河道狭隘部で洗掘が生じ，それを抑止するため床止めを入れる場合に相当する。ここで床止めの施工位置が不適当であると，他の箇所に悪影響の及ぶ場合があるが，本問のような条件では洗掘に歯止めがかかっていることがわかる。

(2)プログラム

 本問の計算プログラムを excercise_21.py に示す。
 限界摩擦速度および無次元掃流量は Particle クラスのコンストラクタで計算している． また単位幅・単位時間当りの掃流砂量は同クラスの MPM メソッドで計算している。

(3)計算結果

 初期河床に対する水面形は下図の通りである。\(x=\) 2000から3200までが狭隘部となっているため，水位の堰上げが生じている。


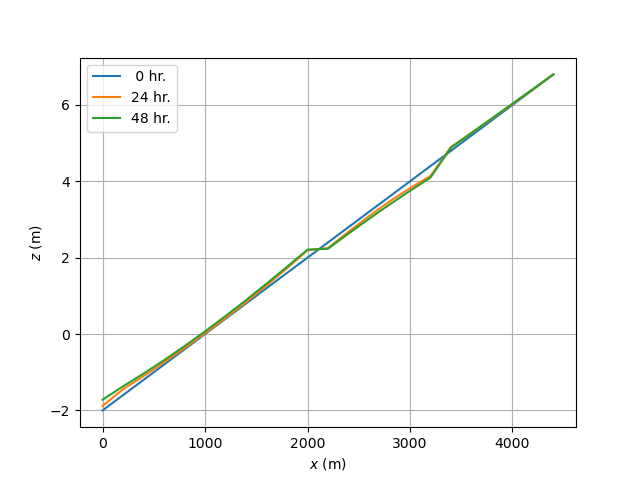
設問1

 上流端での流砂量は動的平衡( \(\Delta z\) = 0，\(q_b\) [i] = \(q_b\) [i+1] )であるため，上流端以外の河床高を式 (5.1) で更新する。
 狭隘部で河床低下傾向となる。

計算結果 設問1

\(x\)
[m]

\(z(t=0h)\)
[m]

\(z(t=24h)\)
[m]

\(z(t=48h)\)
[m]

0

-2.00

-1.88

-1.72

200

-1.60

-1.45

-1.37

400

-1.20

-1.10

-1.04

600

-0.80

-0.74

-0.69

800

-0.40

-0.37

-0.32

1000

0.00

0.02

0.07

1200

0.40

0.42

0.47

1400

0.80

0.84

0.89

1600

1.20

1.27

1.32

1800

1.60

1.72

1.76

2000

2.00

2.19

2.21

2200

2.40

2.25

2.23

2400

2.80

2.68

2.63

2600

3.20

3.09

3.02

2800

3.60

3.47

3.39

3000

4.00

3.82

3.75

3200

4.40

4.14

4.10

3400

4.80

4.90

4.88

3600

5.20

5.27

5.27

3800

5.60

5.64

5.65

4000

6.00

6.02

6.03

4200

6.40

6.41

6.42

4400

6.80

6.80

6.80

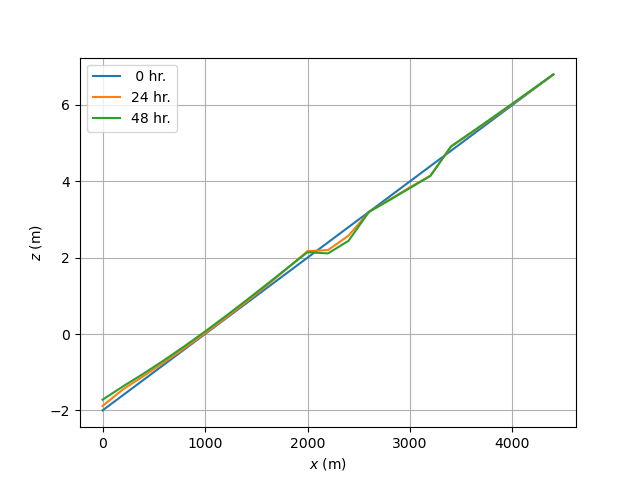
設問2

 上流端での流砂量は静的平衡( \(\Delta z\) = 0，\(q_b\) [i] = 0 )であるため，掃流砂量を算出したあとに上流端の流砂量の補正を行う。
 上流端直下と狭隘部で河床低下傾向となる。

計算結果 設問2

\(x\)
[m]

\(z(t=0h)\)
[m]

\(z(t=24h)\)
[m]

\(z(t=48h)\)
[m]

0

-2.00

-1.88

-1.72

200

-1.60

-1.45

-1.37

400

-1.20

-1.10

-1.04

600

-0.80

-0.74

-0.69

800

-0.40

-0.37

-0.32

1000

0.00

0.02

0.07

1200

0.40

0.42

0.47

1400

0.80

0.84

0.89

1600

1.20

1.27

1.32

1800

1.60

1.72

1.76

2000

2.00

2.19

2.21

2200

2.40

2.25

2.23

2400

2.80

2.68

2.63

2600

3.20

3.09

3.01

2800

3.60

3.47

3.38

3000

4.00

3.82

3.74

3200

4.40

4.14

4.08

3400

4.80

4.89

4.84

3600

5.20

5.25

5.19

3800

5.60

5.59

5.51

4000

6.00

5.90

5.80

4200

6.40

6.15

6.02

4400

6.80

6.80

6.80

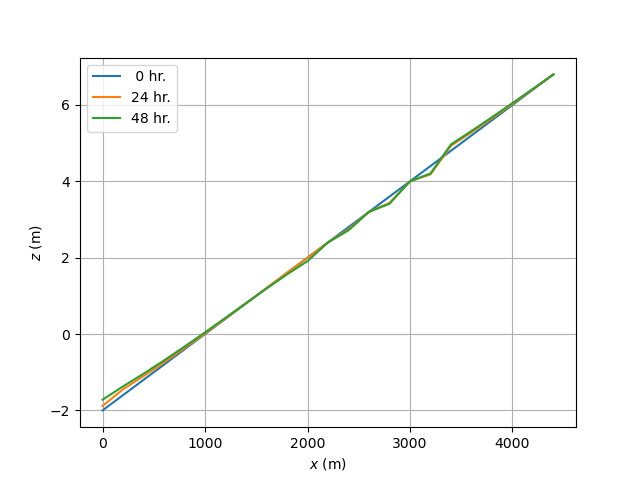
設問3 - 4

 床止め箇所において、床止め高（初期河床高）と河床高を比較し、河床高が床止め以下とならないように式 (5.4) のように流砂量の補正を行う。
 床止めにより河床低下が抑制される。

計算結果 設問3

\(x\)
[m]

\(z(t=0h)\)
[m]

\(z(t=24h)\)
[m]

\(z(t=48h)\)
[m]

0

-2.00

-1.88

-1.72

200

-1.60

-1.45

-1.37

400

-1.20

-1.10

-1.04

600

-0.80

-0.74

-0.69

800

-0.40

-0.37

-0.32

1000

0.00

0.02

0.07

1200

0.40

0.42

0.47

1400

0.80

0.84

0.88

1600

1.20

1.27

1.30

1800

1.60

1.71

1.72

2000

2.00

2.17

2.14

2200

2.40

2.20

2.11

2400

2.80

2.58

2.44

2600

3.20

3.20

3.20

2800

3.60

3.52

3.51

3000

4.00

3.84

3.82

3200

4.40

4.15

4.14

3400

4.80

4.91

4.91

3600

5.20

5.27

5.28

3800

5.60

5.64

5.66

4000

6.00

6.02

6.04

4200

6.40

6.41

6.42

4400

6.80

6.80

6.80

計算結果 設問4

\(x\)
[m]

\(z(t=0h)\)
[m]

\(z(t=24h)\)
[m]

\(z(t=48h)\)
[m]

0

-2.00

-1.88

-1.72

200

-1.60

-1.45

-1.37

400

-1.20

-1.10

-1.04

600

-0.80

-0.74

-0.69

800

-0.40

-0.37

-0.33

1000

0.00

0.02

0.04

1200

0.40

0.41

0.43

1400

0.80

0.81

0.81

1600

1.20

1.21

1.19

1800

1.60

1.61

1.56

2000

2.00

2.00

1.91

2200

2.40

2.40

2.40

2400

2.80

2.74

2.72

2600

3.20

3.20

3.20

2800

3.60

3.44

3.41

3000

4.00

4.00

4.00

3200

4.40

4.18

4.21

3400

4.80

4.93

4.97

3600

5.20

5.28

5.32

3800

5.60

5.65

5.68

4000

6.00

6.03

6.05

4200

6.40

6.41

6.42

4400

6.80

6.80

6.80

問題 22

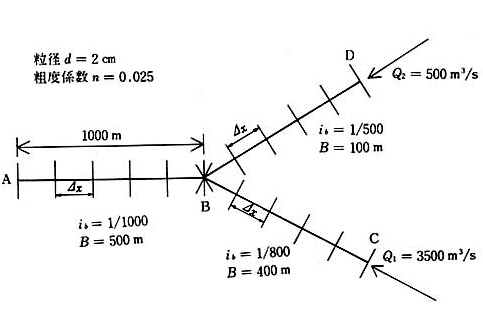
 下図に示す河川に， 上流端 \(C\) から流量 \(Q_1\) = 3,500 m3/s， \(D\) から流量 \(Q_2\) = 500 m3/s の流入があった場合の 5 日後の河床縦断形状を求めよ。 ただし，\(A-B\) 間，\(B-C\) 間はそれぞれ 1,000 m とする。 また，境界条件として下流端 \(A\) の水深は等流水深で与え， 上流端 \(C\) の流砂量は \(\partial Q_B / \partial x\) = 0， \(D\) では \(Q_B\) = 0 を与える。
 計算条件は \(\Delta x\) = 200 m， \(\Delta t\) = 600 s とする。


解 答

(1) 考え方

 各区間の断面番号と河道諸元は以下のように設定する。

 ・AB間：断面\(i\) = 0～5，\(B\) = 500 \(m\)，\(i\) = 1/1000，\(Q\) = 4000 m3/s
 ・BC間：断面\(i\) = 6～11，\(B\) = 400 \(m\)，\(i\) =1/800，\(Q\) = 3500 m3/s
 ・CD間：断面\(i\) = 12～17，\(B\) = 100 \(m\)，\(i\) =1/500，\(Q\) = 500 m3/s

 水位計算は、A→Bまでの水位計算を行ったあと、Bを境界条件としてB→C、B→Dの水位計算を行う。 全断面の水理量から単位幅流砂量を計算し、上流端Cで動的平衡、上流端Dで静的平衡の境界条件を与える。
 河床変動計算は以下のように行う。

  1. i=0～4，7～10，13～16は、河床高を式 (5.1) で更新する。

  2. i=5では，\(\Delta Q_B\) = \(Q_B\)(5) - \(Q_B\)(7) - \(Q_B\)(13) とする。

  3. i=6と断面12は，断面5の河床高としdzは計算しない。

  4. i=11は動的平衡のため，\(\Delta z\) = 0とする。

  5. i=18は静的平衡のため，\(q_b\) = 0とする。

 なお，河床材料の粒径 \(d\) = 2 cm， 粗度係数 \(n\) = 0.025， 流砂は掃流砂のみ，起算水位は下流端で等流水深で与えた。

(2)プログラム

 本問の計算プログラムを excercise_22.py に示す。
 限界摩擦速度および無次元掃流量は Particle クラスのコンストラクタで計算している． また単位幅・単位時間当りの掃流砂量は同クラスの MPM メソッドで計算している。

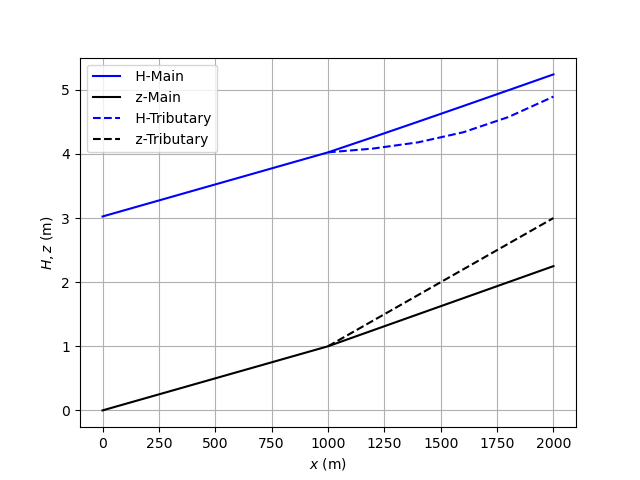
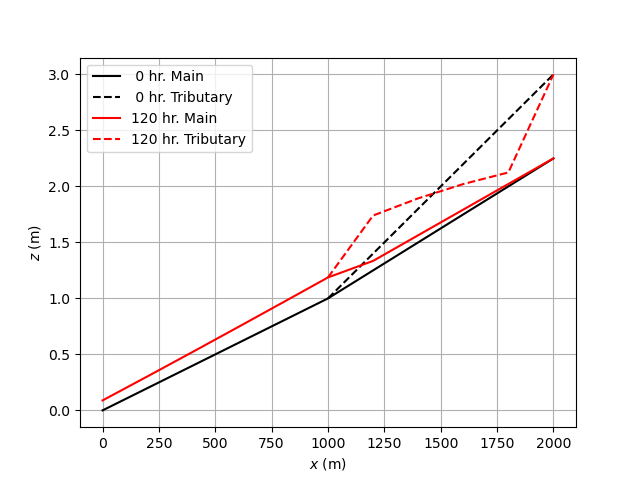
(3)計算結果

 結果を見ると，合流点付近に堆積が起こっていることがわかる。ここは，本線の勾配変化点であり，もともと堆積が起こりやすい箇所となっているが， 支川の流砂量が無視できない場合は，合流後の河床変動や流れに影響を及ぼすことになる。

計算結果 t = 0 hr.

\(i\)

\(Hs\)
[m]

\(H\)
[m]

\(z\)
[m]

\(\Delta z\)
[m]

\(\tau_*\)

\(q_b\)
[m3/s/m]

0

3.024

3.024

0.000

0.000

0.0916

7.7239e-04

1

3.024

3.224

0.200

0.000

0.0916

7.7239e-04

2

3.024

3.424

0.400

0.000

0.0916

7.7239e-04

3

3.024

3.624

0.600

0.000

0.0916

7.7239e-04

4

3.024

3.824

0.800

0.000

0.0916

7.7239e-04

5

3.024

4.024

1.000

0.000

0.0916

7.7239e-04

6

3.024

4.024

1.000

0.000

0.1096

1.3240e-03

7

3.012

4.262

1.250

0.000

0.1107

1.3600e-03

8

3.003

4.503

1.500

0.000

0.1115

1.3853e-03

9

2.997

4.747

1.750

0.000

0.1120

1.4028e-03

10

2.993

4.993

2.000

0.000

0.1123

1.4147e-03

11

2.990

5.240

2.250

0.000

0.1126

1.4229e-03

12

3.024

4.024

1.000

0.000

0.0358

0.0000e+00

13

2.684

4.084

1.400

0.000

0.0473

0.0000e+00

14

2.381

4.181

1.800

0.000

0.0626

1.2761e-04

15

2.138

4.338

2.200

0.000

0.0804

4.8217e-04

16

1.975

4.575

2.600

0.000

0.0967

9.1853e-04

17

1.894

4.894

3.000

0.000

0.1067

1.2285e-03

計算結果 t = 120 hr.

\(i\)

\(Hs\)
[m]

\(H\)
[m]

\(z\)
[m]

\(\Delta z\)
[m]

\(\tau_*\)

\(q_b\)
[m3/s/m]

0

3.024

3.113

0.089

0.089

0.0916

7.7239e-04

1

3.006

3.311

0.305

0.105

0.0929

8.0777e-04

2

2.990

3.513

0.522

0.122

0.0941

8.4099e-04

3

2.976

3.719

0.742

0.142

0.0951

8.7143e-04

4

2.964

3.928

0.964

0.164

0.0961

8.9861e-04

5

2.953

4.140

1.187

0.187

0.0969

9.2217e-04

6

2.953

4.140

1.187

0.187

0.1159

1.5374e-03

7

3.085

4.420

1.335

0.085

0.1046

1.1605e-03

8

3.079

4.643

1.564

0.064

0.1051

1.1759e-03

9

3.075

4.868

1.793

0.043

0.1055

1.1874e-03

10

3.072

5.094

2.022

0.022

0.1057

1.1951e-03

11

3.071

5.321

2.250

0.000

0.1058

1.1989e-03

12

2.953

4.140

1.187

0.187

0.0378

0.0000e+00

13

2.456

4.196

1.740

0.340

0.0582

6.7124e-05

14

2.459

4.352

1.893

0.093

0.0580

6.4931e-05

15

2.489

4.510

2.021

-0.179

0.0564

4.6232e-05

16

2.538

4.663

2.125

-0.475

0.0539

2.1791e-05

17

1.756

4.756

3.000

0.000

0.1272

0.0000e+00

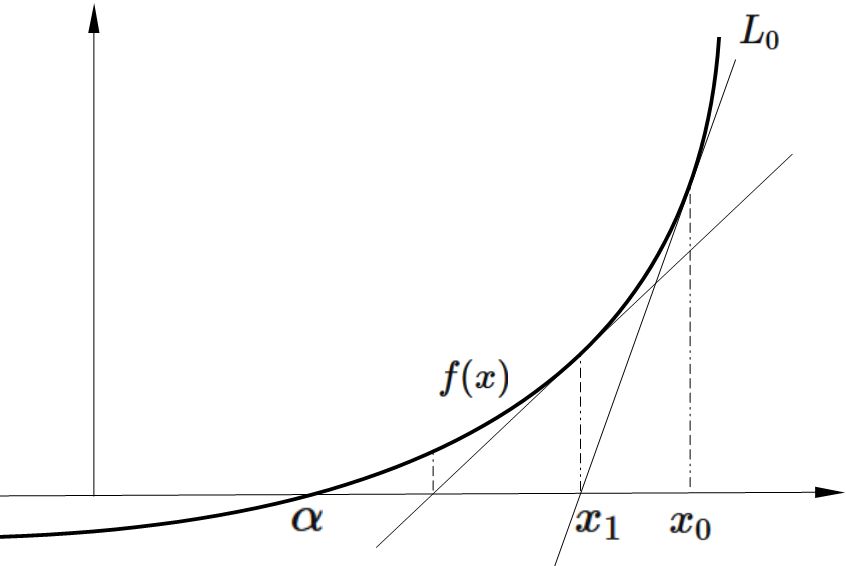
補遺 1　ニュートン法

 非線形関数 \(f(x)\) の導関数を \(f'(x)\) とする時，

\[ f'(x) \sim \frac{f(x + \Delta x) - f(x)}{\Delta x} \]

である。よって、

\[ f(x + \Delta x) \sim f(x) + f'(x) \Delta x \]

が成り立つ（これを「テイラー展開」という）。 特に \(f(x + \Delta x) = 0\) である時，

\[ \Delta x = -f(x) / f'(x) \]

である。 これより，\(f(x) = 0\) の近似解は， \(\Delta x\) の絶対値が所定の微小値 \(\varepsilon\) 以下になるまで， 次の演算を繰り返すことで求めることができる（下図）。 このアルゴリズムをニュートン法 という。

\[ x \leftarrow x - f(x) / f'(x) \]