この節の作者: 清水康行 <yasu@i-ric.org>

2次元移流方程式

基礎式

2次元移流方程式を次式で表します.

(123)\[{{\partial f}\over{\partial t}} + u{{\partial f}\over{\partial x}}+ v{{\partial f}\over{\partial y}} = 0\]

ここで, \(t\) は時間, \(x, y\) は直交座標軸, \(f\) は移流される変数, \(u,v\) は \(x, y\) 方向の移流速度です.

1次元の移流方程式と同様，この方程式の理論解は \(f\) はその分布形を保ったまま， \(x\) 方向には \(u\) の速度で, \(ｙ\) 方向には \(v\) の速度で移動 するという結果となります．

風上差分

移流項の風上差分式は下記となります．

(124)\[\begin{split}u>0 \mbox{のとき}; \; \; u\cfrac{\partial f}{\partial x}=u\cfrac {f(i,j)-f(i-1,j)}{\Delta x} \\ u<0 \mbox{のとき}; \; \; u\cfrac{\partial f}{\partial x}=u\cfrac {f(i+1,j)-f(i,j)}{\Delta x}\end{split}\]

(125)\[\begin{split}v>0 \mbox{のとき}; \; \; v\cfrac{\partial f}{\partial x}=v\cfrac {f(i,j)-f(i,j-1)}{\Delta y} \\ v<0 \mbox{のとき}; \; \; v\cfrac{\partial f}{\partial x}=v\cfrac {f(i,j+1)-f(i,j)}{\Delta y}\end{split}\]

ここで, \(\Delta x, \Delta y, \Delta t\) はそれぞれ \(x, y, t\) 方向の計算刻み幅で, \((i,j)\) はそれぞれ \((x,y)\) 方向の格子番号です． したがって, 例えば, \(u>0, \; v>0\) の場合, (123) 式の 差分式は下記のようになります．

(126)\[\cfrac{f_n(i,j)-f(i,j)}{\Delta t}+ u\cfrac{f(i,j)-f(i-1,j)}{\Delta x}+ v\cfrac{f(i,j)-f(i,j-1)}{\Delta y}=0\]

ただし, \(f_n(i,j)\) は \(t=t+\Delta t\) における \(f(i,j)\) の値です． (126) 式より \(f_n(i,j)\) は次式を:math:Delta t 毎に 繰り返し計算することにより求めることが出来ます. なお，この場合は \(x\) 方向にも \(y\) 方向にも後進差分ということになります．

(127)\[f_n(i,j)=f(i,j)-\Delta t \left\{ u\cfrac{f(i,j)-f(i-1,j)}{\Delta x}+ v\cfrac{f(i,j)-f(i,j-1)}{\Delta y}\right\}\]

後進差分による計算例

\(u>0, \; v>0\) の場合の計算例を示します．\(f\) の初期分布は Figure 38 図に示すような 円錐形の分布を与えます．

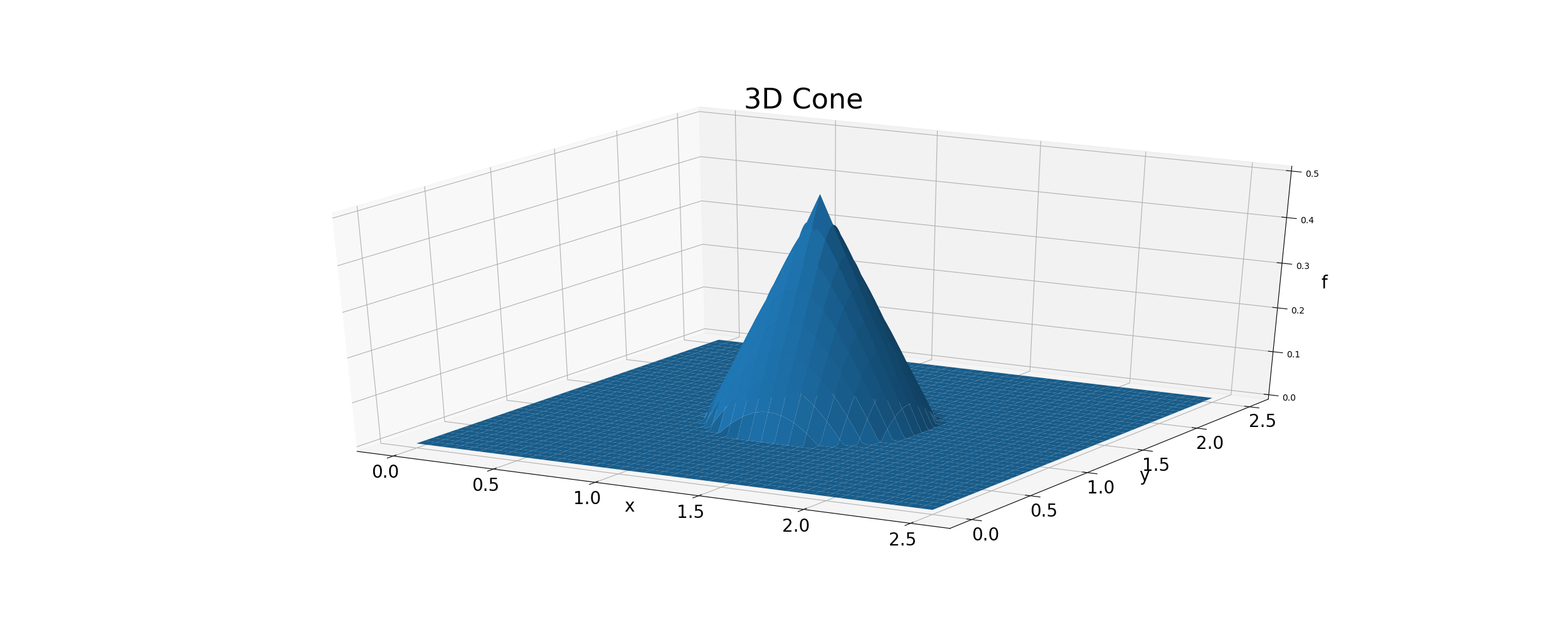
Figure 38 : 2次元移流計算の初期条件

ちなみに，円錐形分布は次式で与えます．

(128)\[\begin{split}r<R \; \mbox{のとき;} & f(x,y)=\cfrac{R-r}{R} f_p \\ r>R \; \mbox{のとき;} & f(x,y)=0\end{split}\]

ただし,

(129)\[r=\sqrt{(X_p-x)^2+(Y_p-y)^2}\]

また，\(X_p, Y_p\) ピークの位置, \(f_p\) はピークの値, \(R\) は底面の半径です．

Pythonコードと計算例

(127) を使ったPythonコードを https://github.com/YasuShimizu/Python-Code/blob/main/2d_backward_p3d.py に示します．また，このコードを用いて計算された計算結果を下図に示します． なお，この例では \(u=v=0.5\) (m/s), \(f_p=0.5, R=20\) (m)としてます．

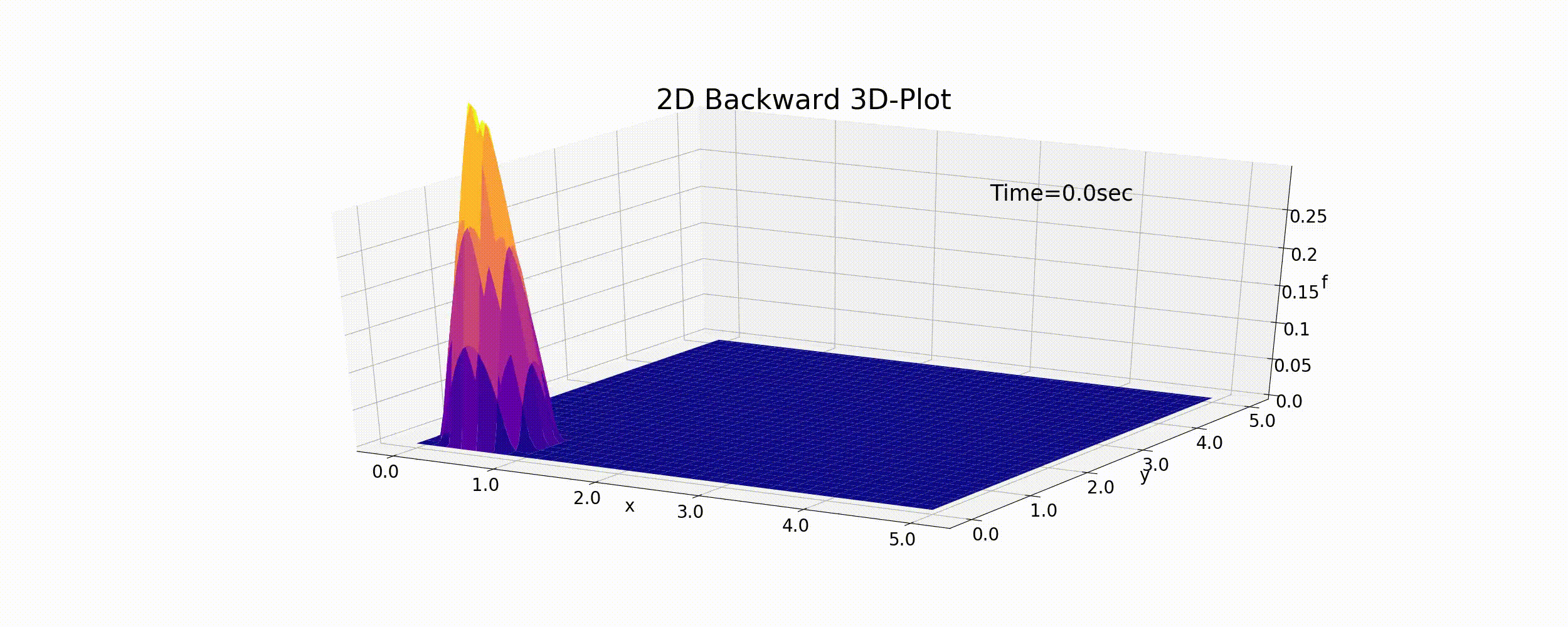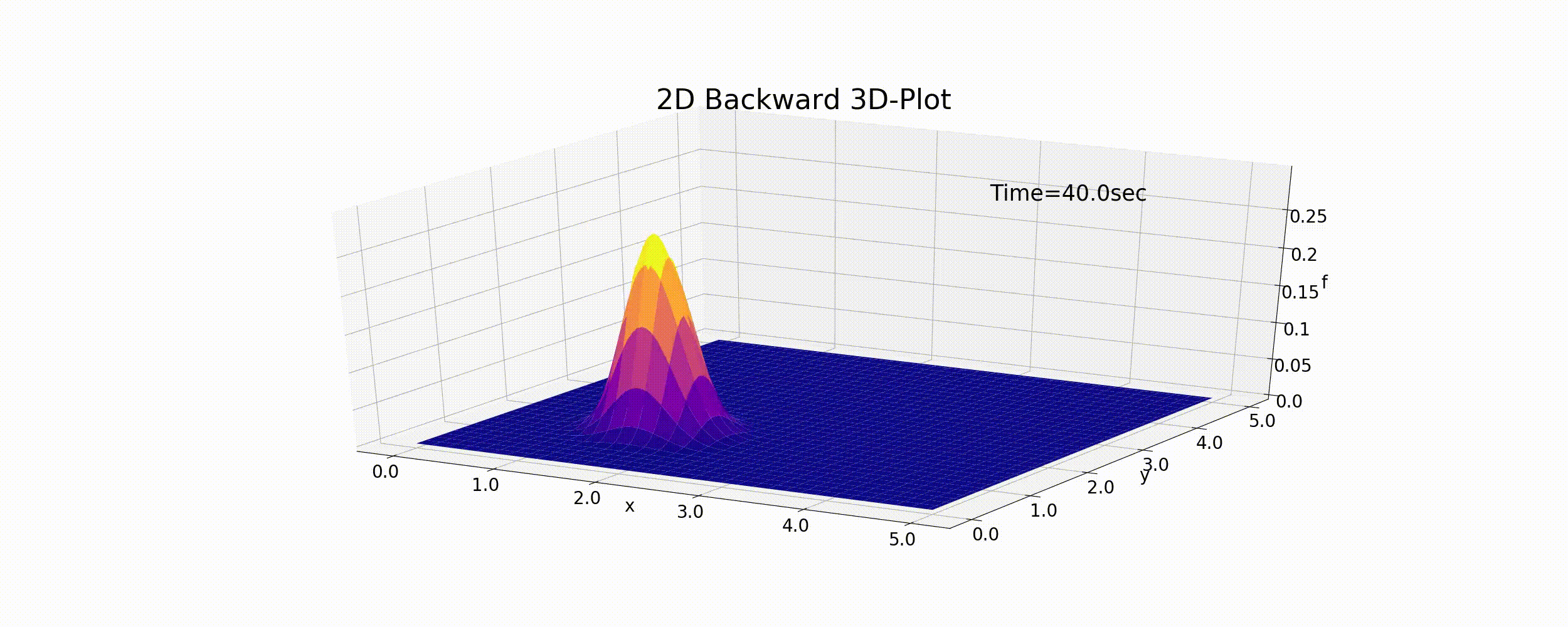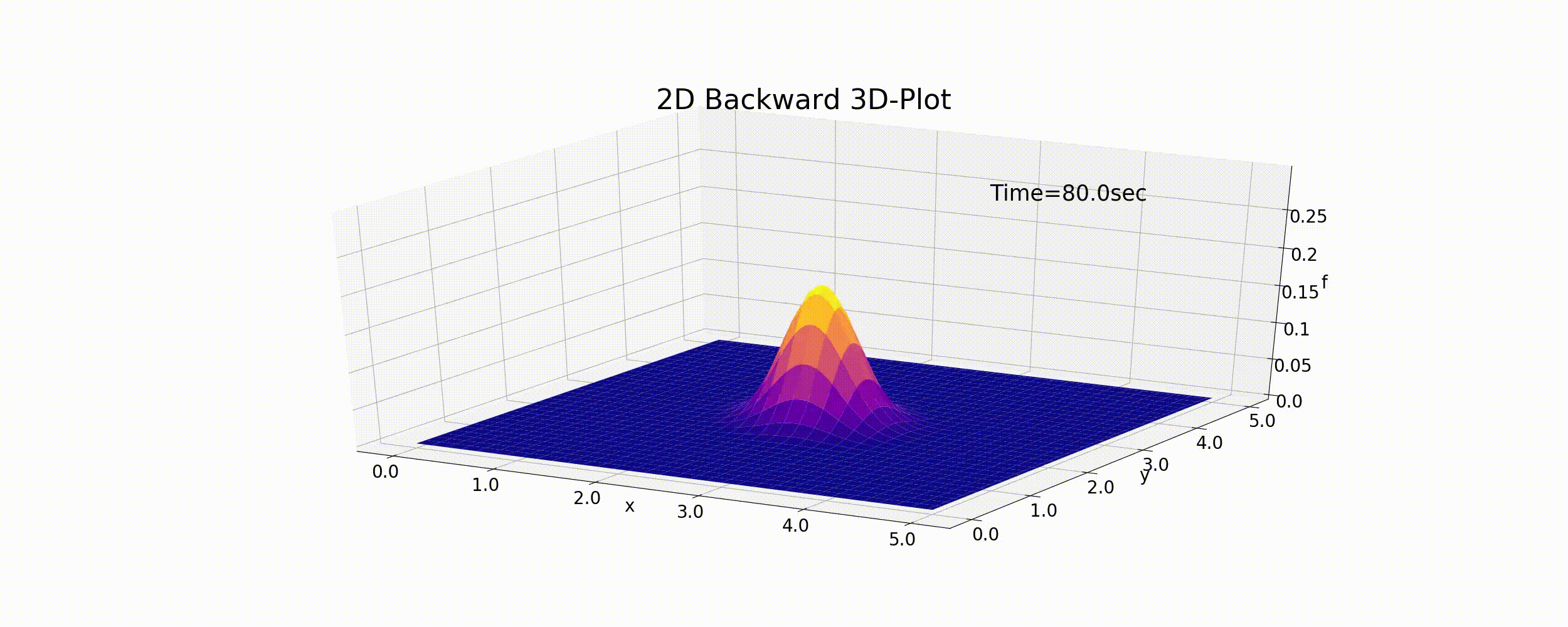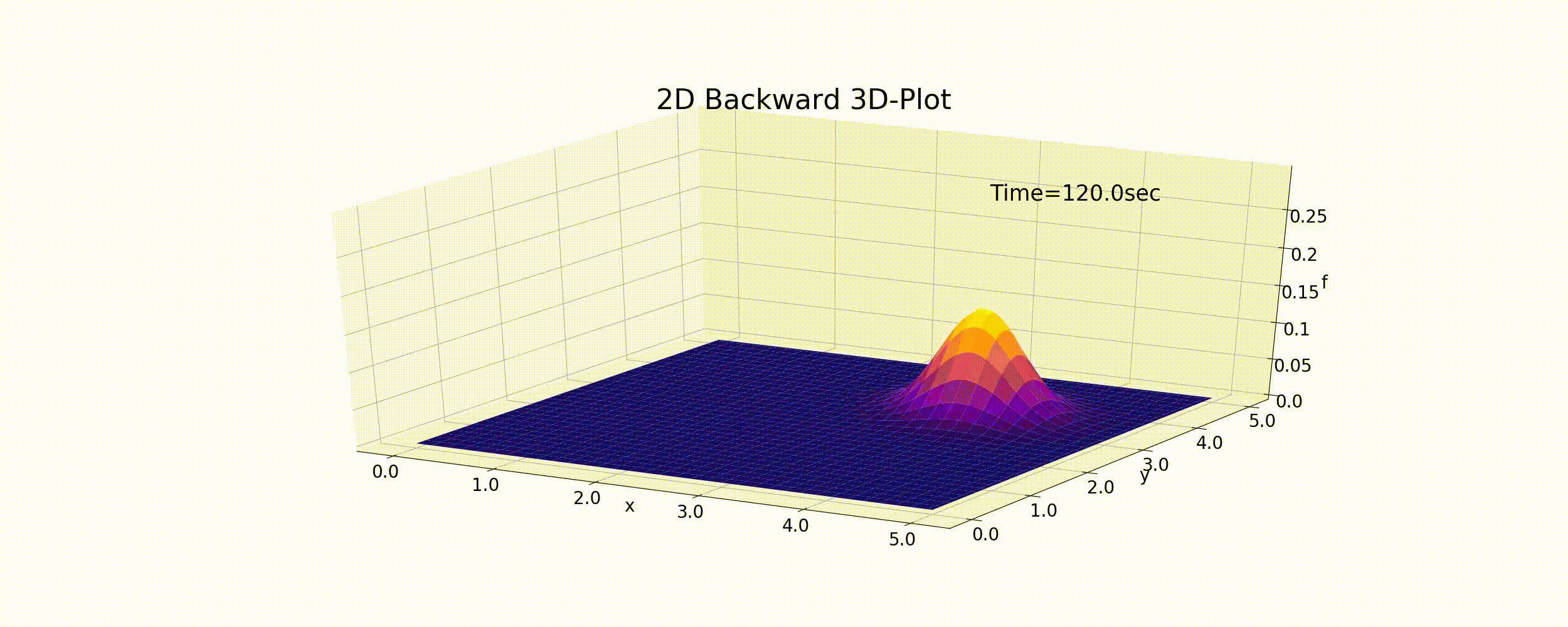
Figure 39 : 2次元移流方程式の計算結果(後進差分)

１次元の時と同様，この計算結果は数値拡散の影響でピークの値が徐々に下がりながら，円錐の形も 潰れながら移動していおり，けっして正確な計算結果とは言えません．

移流方向が変化する場合の風上差分法

(124) 式, (125) 式の移流項を一つの式で表した，\(f\) の更新 式は下記となります．

\[f_n(i,j)=f(i,j)\]

\[-\cfrac{\Delta t}{2 \Delta x} \left[(u+|u|)\left\{f(i,j)-f(i-1,j)\right\}+(u-|u|)\left\{f(i+1,j)-f(i,j)\right\} \right.\]

(130)\[+\left.(v+|v|)\left\{f(i,j)-f(i,j-1)\right\}+(v-|v|)\left\{f(i,j+1)-f(i,j)\right\} \right]\]

(130) 式は \(u, v\) の大きさや符号に関わらず適用可能な風上差分法です．

では，この2次元風上差分法を \(u, v\) が変化する状況で試してみましょう． いま，\(u,v\) が次式で 振動する状況を想定します．

(131)\[\begin{split}u = & -r_t \omega \sin \theta \\ v = & r_t \omega \cos \theta\end{split}\]

この式で表される運動は円運動で, \(r_t\) は円運動の曲率半径， \(\omega\) は角速度, \(\theta\) は位相角です． もし, Figure 38 図に示した円錐形のピークが，(131) 式に従って運動するとした場合の結果は下図( Figure 40 )のようになります． なお, この例では, \(T\) を円運動の1周の周期として \(T=\) 100sec, \(r_t\) = 30m, f_p =0.5 とした計算です． また，\(T\) と \(\omega\) の関係は次式で表されます．

(132)\[\omega=\cfrac{2\pi}{T}\]

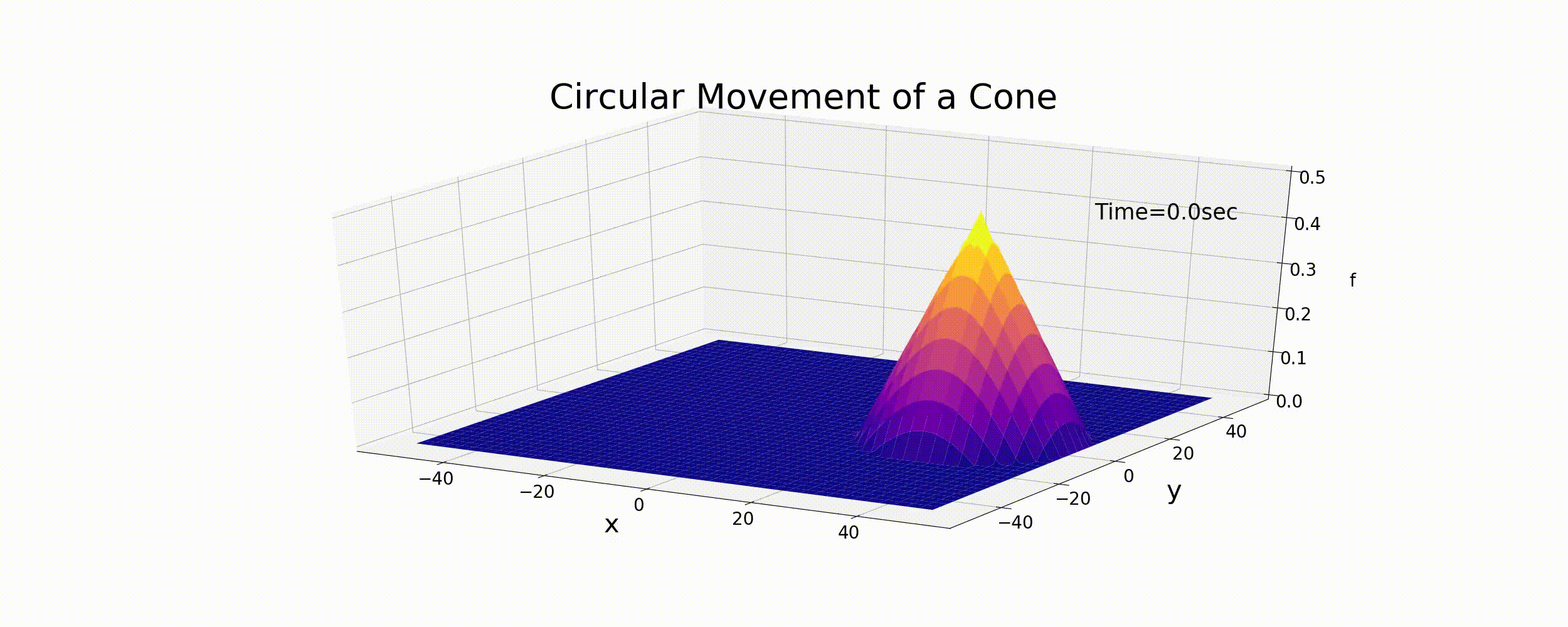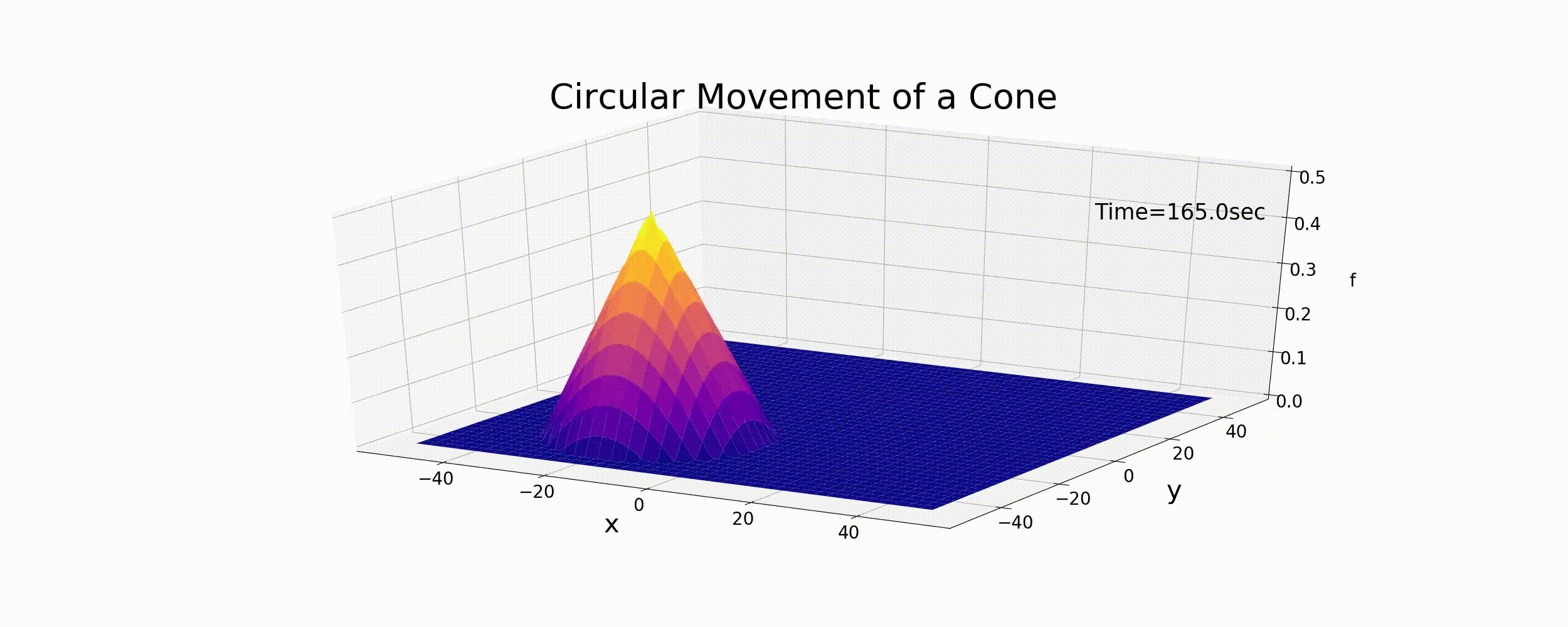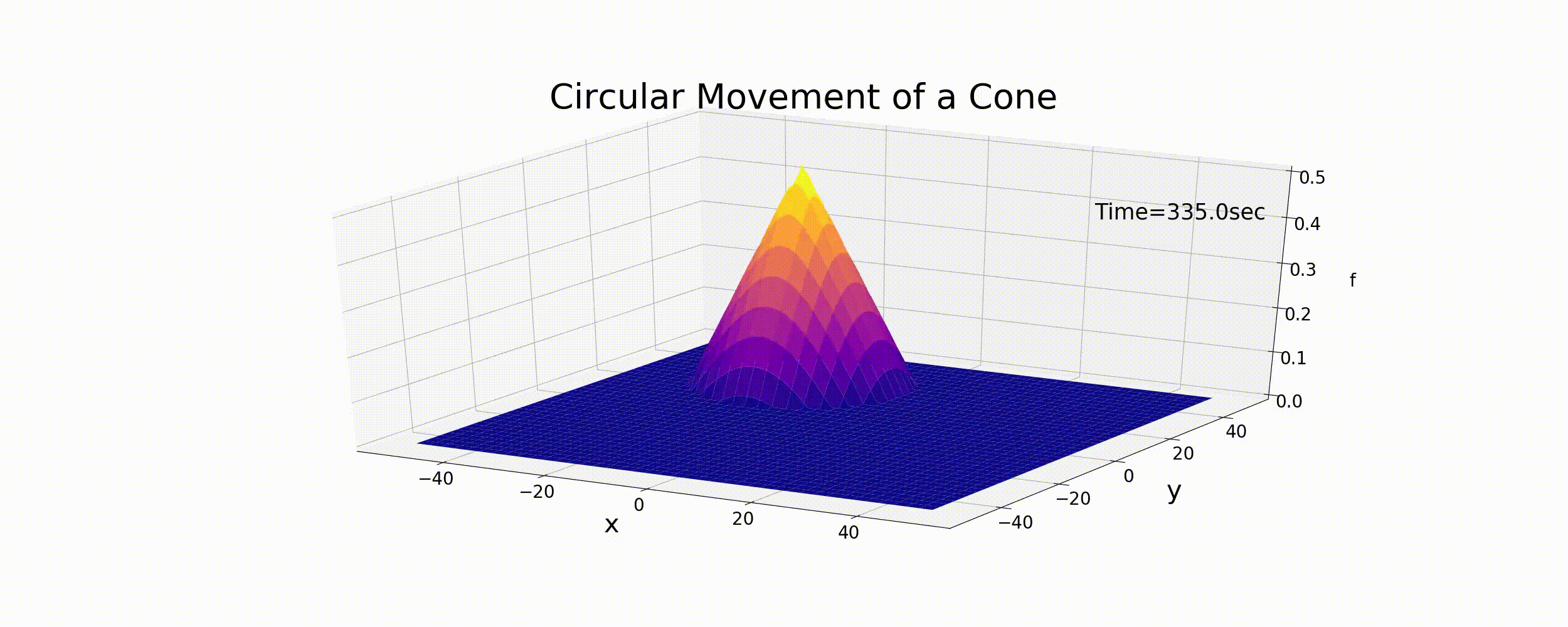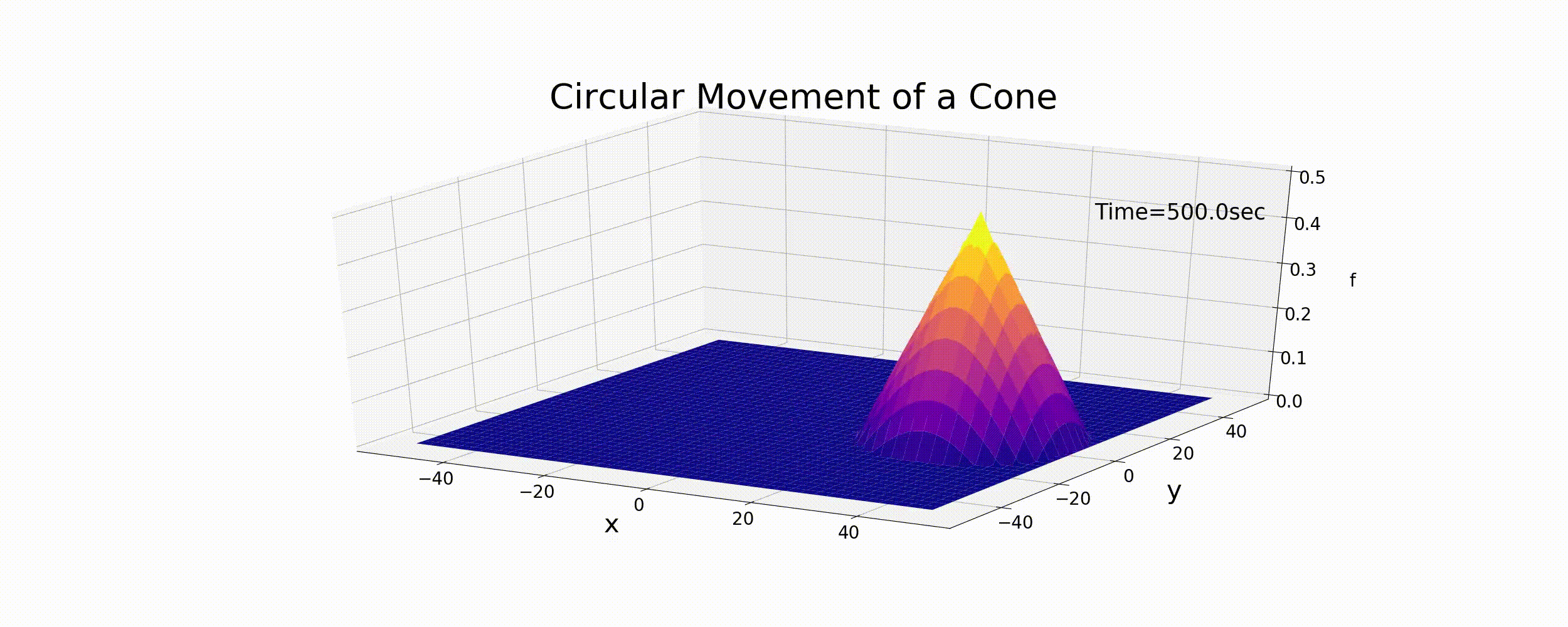
Figure 40 : 円錐形状の円運動

Figure 40 は単に円錐形の分布を (131) 式の速度で 動かしただけで，(123) 式の差分計算結果ではありませんが，ある意味これが これから行う数値計算の目標となる厳密解です． なお参考までに，Figure 40 図のアニメーションを 作成するPythonコードを下記に示します．

https://github.com/YasuShimizu/Python-Code/blob/main/3dcone_circle_m3d.py

前置きが長くなってしまいましたが，本節の目標である2次元移流方程式の風上差分解法を やってみましょう．

Pythonコードと計算例

(123) 式を用いたPythonコードを下記に示します．

https://github.com/YasuShimizu/Python-Code/blob/main/2d_upwind_circle.py

このコードを使って，(128) 式の初期条件で, \(u,v\) を (131) 式 で変化させながら計算した結果は下図となります．

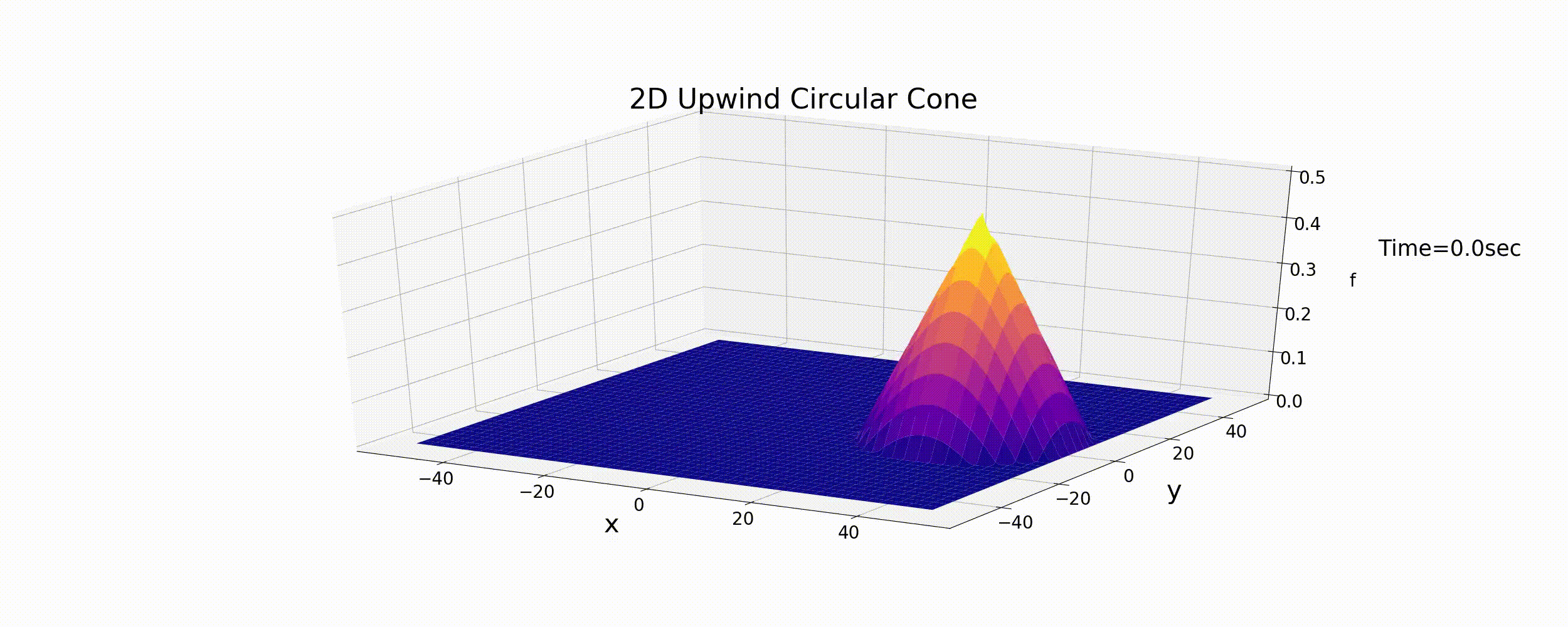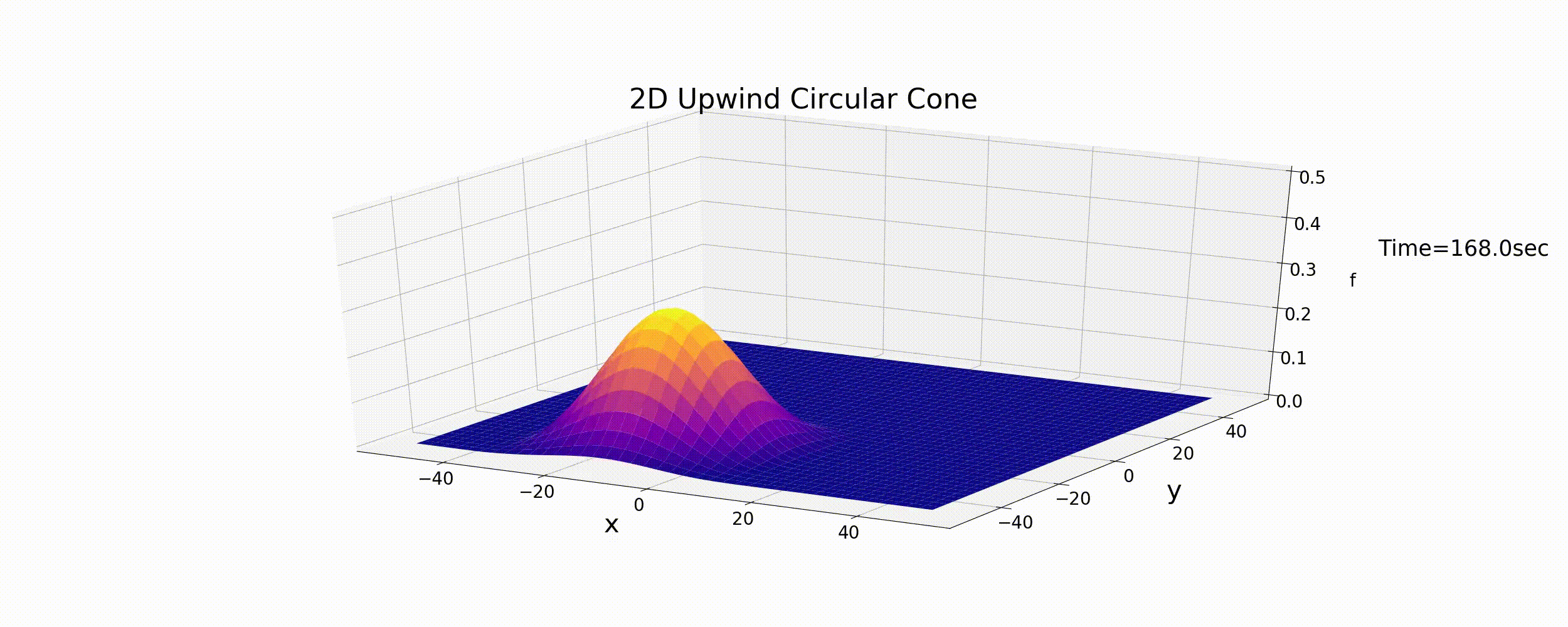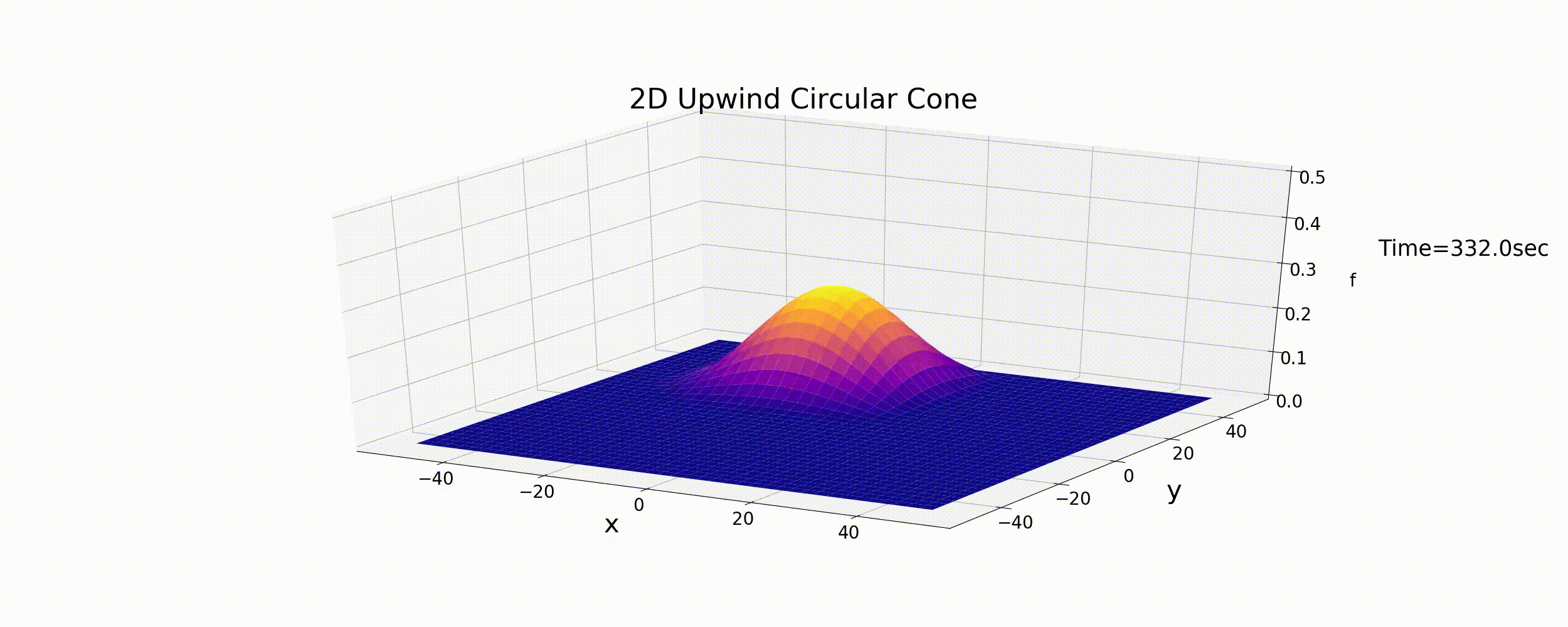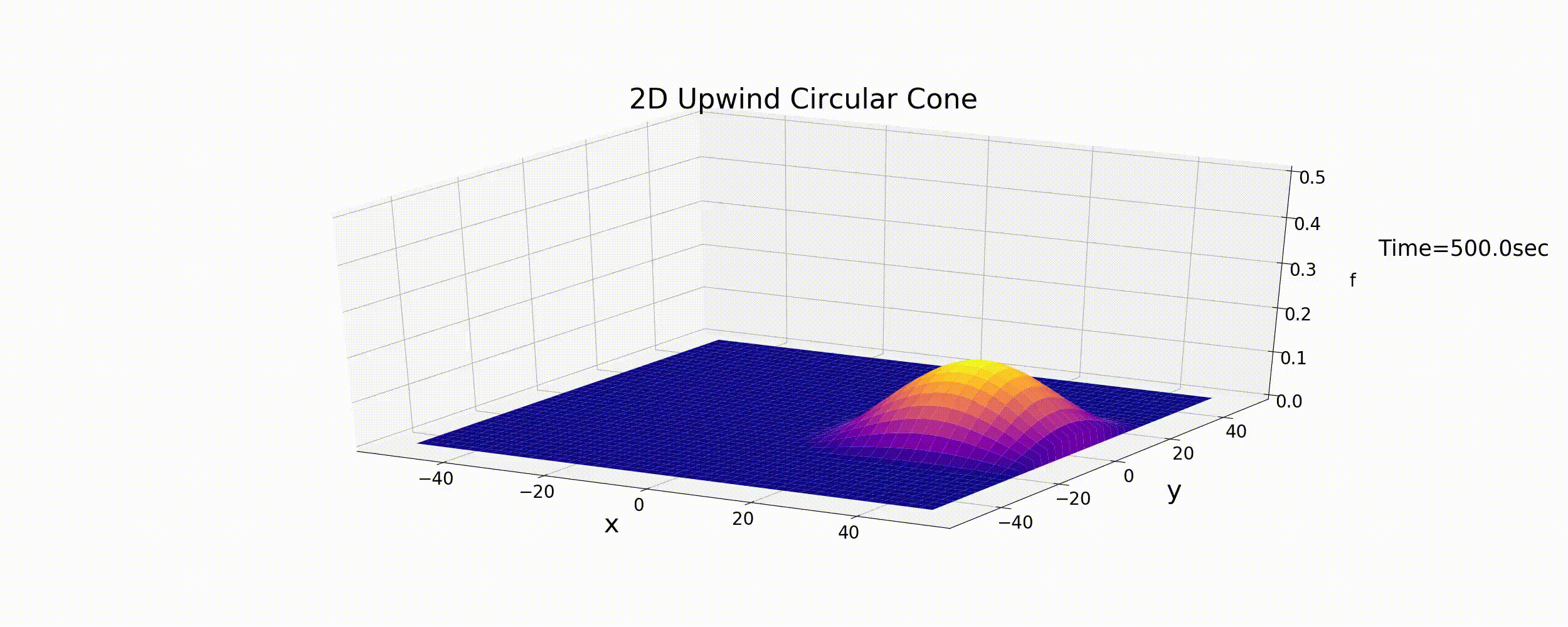
Figure 41 : 2次元風上差分法による円錐形分布の円運動の計算

予想どおりではありますが，風上差分法で初期形状が徐々に拡散し，ピークの値も減衰してしまってます． 計算結果は安定していますが，1次元の時と同様，風上差分法では正確な計算結果が得られないことが示されました．

演習問題(4)

初期条件を円錐形分布とする変数 \(f\) が四角形の形状の辺に沿って連続的に移動する場合の \(f\) の時間変化を計算して下さい．

高精度の差分法

ここで，1次元の場合と同様に2次元の高精度差分法として2次元版のCIP法について述べます．

2次元CIP法による移流項の計算( \(u<0, v<0\) の場合)

説明は簡単のためにまず \(u<0\) , \(v<0\) の場合について行います.

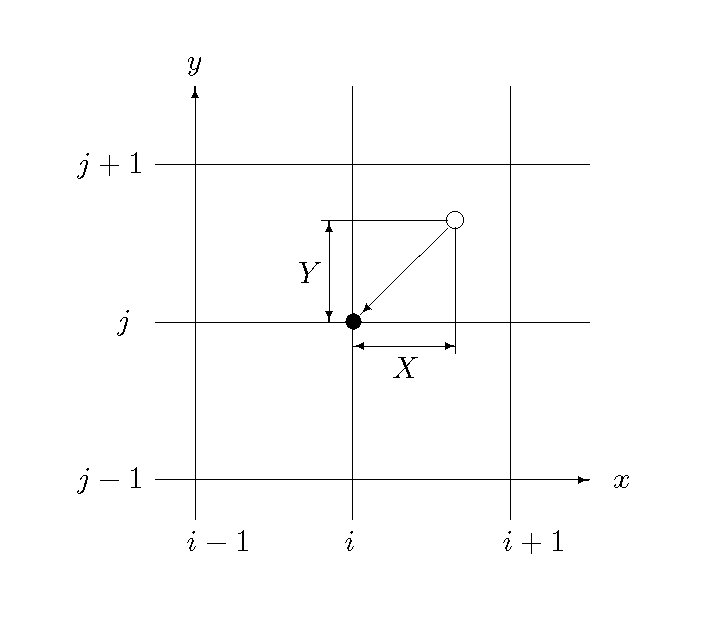
Figure 42 : 計算平面上での \(f\) の推定

Figure 42 示すように \(x, y\) 方向の計算点番号を \(i,j\) として 時刻 \(t\) で \(i, i+1, j, j+1\) の範囲にある点(図中の白丸)が \(\Delta t\) 時間で図中の黒丸の点に移動すると考えます.

1次元の計算で説明したのとまったく同じようにこの問題は Figure 42 の 黒丸の点における \(f\) の分布形をいかに推定するかという問題に帰着します. 即ち,

(133)\[X=-u \Delta t, \; \; Y=-v \Delta t\]

のときこの分布形 \(F(X,Y)\) が推定できれば

(134)\[f(i,j,t+\Delta t) = F(X, Y)\]

により \(f\) の時間更新ができます. ここで, \(f\) は　\((i,j)\) 格子の離散値, \(F\) は連続関数であることに注意して下さい．

\(F\) の関数形は1次元問題のときは3次曲線としましたが, ここでは3次曲面とします. \(F(X,Y)\) は \(X=0, Y=0\) で

(135)\[F(X,Y)=f(i,j), \; \; \; F_x(X,Y)=f_x(i,j), \; \; \;F_y(X,Y) = f_y(i,j)\]

(ただし, \(F_x(X,Y)=\displaystyle{{\partial F}\over{\partial x}}\) , \(F_y(X,Y)=\displaystyle{{\partial F}\over{\partial y}} (X,Y)\) , \(f_x(i,j)=\displaystyle{{\partial f}\over{\partial x}} (i,j)\) , \(f_y(i,j)=\displaystyle{{\partial f}\over{\partial y}} (i,j)\) です．)

を満たす必要があるので, \(F(X,Y)\) を次式のように置きます.

(136)\[\begin{split}F(X,Y) = \left[ (a_1 X + c_1 Y + e_1) X + g_1 Y + f_x(i,j) \right] X + \\ \left[ (b_1 Y + d_1 X + f_1) Y + f_y(i,j) \right] Y + f(i,j)\end{split}\]

この式は (135) 式を自動的に満たしています. 他の条件としては,

(137)\[\begin{split}F(0,-\Delta y)=f(i,j+1), \; \; \; F(-\Delta x, 0)=f(i+1,j) \\ F(-\Delta x, -\Delta y) = f(i+1,j+1), \; \; \; F_x(0, -\Delta y)=f_x(i,j+1) \\ F_x(-\Delta x, 0)=f_x(i+1,j), \; \; \; F_x(-\Delta x, -\Delta y) = f_x(i+1,j+1) \\ F_y(0, -\Delta y)=f_y(i,j+1), \; \; \; F_y(-\Delta x, 0)=f_y(i+1,j)\end{split}\]

などを満たす必要があります. これらの関係を用いることにより, (136) 式中の係数は以下の ようになります.

\[a_1 = {{ \left[ f_x(i+1,j)+f_x(i,j) \right] \Delta x +2 \left[ f(i,j)-f(i+1,j) \right]}\over{\Delta x^3}}\]

\[b_1 = {{ \left[ f_y(i,j+1)+f_y(i,j) \right] \Delta y +2 \left[ f(i,j)-f(i,j+1) \right]}\over{\Delta y^3}}\]

\[c_1 = {{-\left\{ f(i,j)-f(i,j+1)-f(i+1,j)+f(i+1,j+1)\right\}-\left[f_x(i,j+1)-f_x(i,j) \right] \Delta x }\over{\Delta x^2 \Delta y}}\]

\[d_1 = {{-\left\{f(i,j)-f(i,j+1)-f(i+1,j)+f(i+1,j+1)\right\}- \left[ f_y(i+1,j)-f_y(i,j) \right] \Delta y}\over{\Delta x \Delta y^2}}\]

\[e_1 = {{ 3 \left[ f(i+1,j)-f(i,j) \right] + \left[ f_x(i+1,j)+2 f_x(i,j) \right] \Delta x }\over{\Delta x^2}}\]

\[f_1 = {{ 3 \left[ f(i,j+1)-f(i,j) \right] + \left[ f_y(i,j+1)+2 f_y(i,j) \right] \Delta y }\over{\Delta y^2}}\]

(138)\[g_1 = {{-\left\{f_y(i+1,j)-f_y(i,j)\right\}+c_1 \Delta x^2 }\over{\Delta x}}\]

演習問題(5)

(138) 式の誘導を自分で行って, \(a_1 \sim g_1\) の表現が正しいかどうか確かめて下さい.

2次元CIP法による移流項の計算(一般化)

ここまでの説明は \(u<0\) , \(v<0\) の場合でしたが, 実際には \(u, v\) の符号の組み合わせに よって8通りの組み合わせがありますが, これをすべて定式化してプログラミング するのは非常に煩雑です. そこで1次元でやったように符号関数( \(\mbox{sign}\) )関数を導入して 表現することにします.

(139)\[\begin{split}i_s = \mbox{sign}(u), \; \; \; & j_s = \mbox{sign}(v) \\ i_m = i-i_s, \; \; \; & j_m = j-j_s\end{split}\]

格子間の変数の分布形状 \(F(X,Y)\) は \(X, Y\) を Figure 43 のように定義し, (30) 式を2次元に拡張することにより, (140) のように定義します．

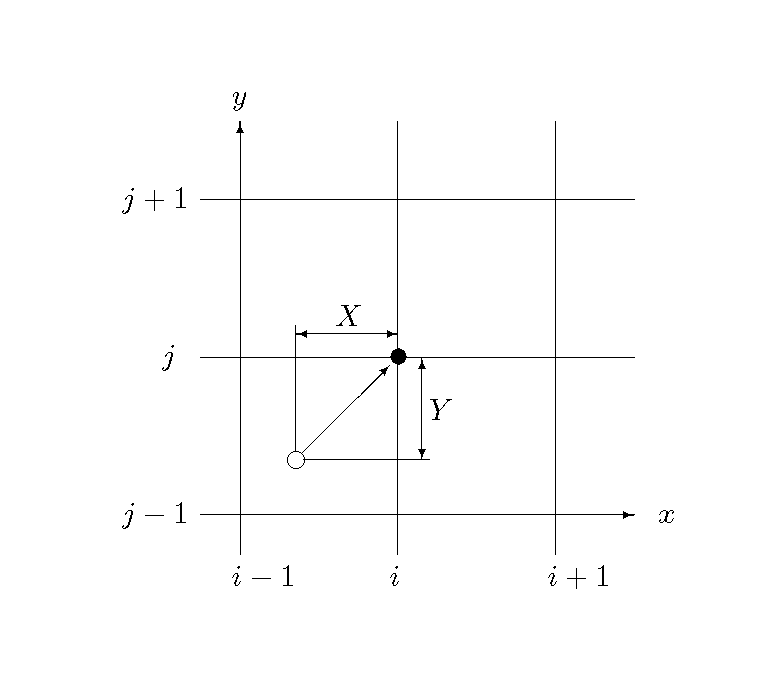
Figure 43 : 計算平面上での \(X, Y\) の定義

(140)\[\begin{split}F(X,Y) = \left[ (a_1 X + c_1 Y + e_1) X + g_1 Y + f_x(i,j) \right] X + \\ \left[ (b_1 Y + d_1 X + f_1) Y + f_y(i,j) \right] Y + f(i,j)\end{split}\]

ただし, 係数 \(a_1 \sim g_1\) は \(i_s, j_s, i_m, j_m\) を用いることにより, \(u, v\) の符号に関係なく以下のように表現されます.

\[a_1 = {{ i_s \left[ f_x(i_m,j)+f_x(i,j) \right] \Delta x -2 \left[ f(i,j)-f(i_m,j) \right]}\over{i_s \Delta x^3}}\]

\[b_1 = {{ j_s \left[ f_y(i,j_m)+f_y(i,j) \right] \Delta y -2 \left[ f(i,j)-f(i,j_m) \right]}\over{j_s \Delta y^3}}\]

\[c_1 = {{ -\left\{f(i,j)-f(i,j_m)-f(i_m,j)+f(i_m,j_m)\right\}-i_s \left[f_x(i,j_m)-f_x(i,j) \right] \Delta x }\over{j_s \Delta x^2 \Delta y}}\]

\[d_1 = {{ -\left\{f(i,j)-f(i,j_m)-f(i_m,j)+f(i_m,j_m)\right\}- j_s \left[ f_y(i_m,j)-f_y(i,j) \right] \Delta y}\over{i_s \Delta x \Delta y^2}}\]

\[e_1 = {{ 3 \left[ f(i_m,j)-f(i,j) \right] + i_s \left[ f_x(i_m,j)+2 f_x(i,j) \right] \Delta x }\over{\Delta x^2}}\]

\[f_1 = {{ 3 \left[ f(i,j_m)-f(i,j) \right] + j_s \left[ f_y(i,j_m)+2 f_y(i,j) \right] \Delta y }\over{\Delta y^2}}\]

(141)\[g_1 = {{-\left\{f_y(i_m,j)-f_y(i,j)\right\}+c_1 \Delta x^2 }\over{i_s \Delta x}}\]

演習問題(6)

(141) 式の誘導を自分で行って, \(a_1 \sim g_1\) の表現が正しいかどうか確かめて下さい.

微分量の更新

CIP法では変数 \(f\) の他にもその微分量 \(f_x, f_y\) も時々刻々更新して行く必要 があります. そこで (123) 式の両辺をまず \(x\) で偏微分します.

(142)\[{{\partial^2 f}\over{\partial t \partial x}} + {{\partial u}\over{\partial x}} {{\partial f}\over{\partial x}} + u {{\partial^2 f}\over{\partial x^2}} + {{\partial v}\over{\partial x}} {{\partial f}\over{\partial y}} + v {{\partial^2 f}\over{\partial x \partial x}} =0\]

\(\displaystyle{{{\partial f}\over{\partial x}}}\) を \(f_x\) とすると,

(143)\[{{\partial f_x}\over{\partial t}} + u{{\partial f_x}\over{\partial x}} + v{{\partial f_x}\over{\partial y}} = -\left( f_x {{\partial u}\over{\partial x}} + f_y {{\partial v}\over{\partial x}} \right)\]

となりまして, 左辺は :f_x に関する2次元の移流方程式になっていることが分かります. 従って, 前述の2次元のCIP法をそのまま適用すれば良いことに なります. また, 右辺に関してはもし \(u, v\) が定数であればゼロとなりますが, 変数の場合には, 1次元のCIP法で説明した[ CIP法 の基本概念 ]を適用して 分離解法で計算することになります. なお右辺の差分形式は中央差分で行けます.

同様に, (123) 式を \(y\) で偏微分して \(\displaystyle{{{\partial f}\over{\partial y}}}\) を \(f_y\) とすると,

(144)\[{{\partial f_y}\over{\partial t}} + u{{\partial f_y}\over{\partial x}} + v{{\partial f_y}\over{\partial y}} = -\left( f_x {{\partial u}\over{\partial y}} + f_y {{\partial v}\over{\partial y}} \right)\]

が得られ (143) 式と同様な形となり, 左辺の移流項の部分はCIP法で, 右辺の Source項の部分は中央差分で計算可能となります.

Pythonコードと計算例

以上で述べた2次元CIP法のPhthonコードを下記に示します．

https://github.com/YasuShimizu/2d_advection_cip

このコードによる計算結果を下記に示します．計算条件は前記の 風上差分 と同じく円運動をする円錐形分布です．

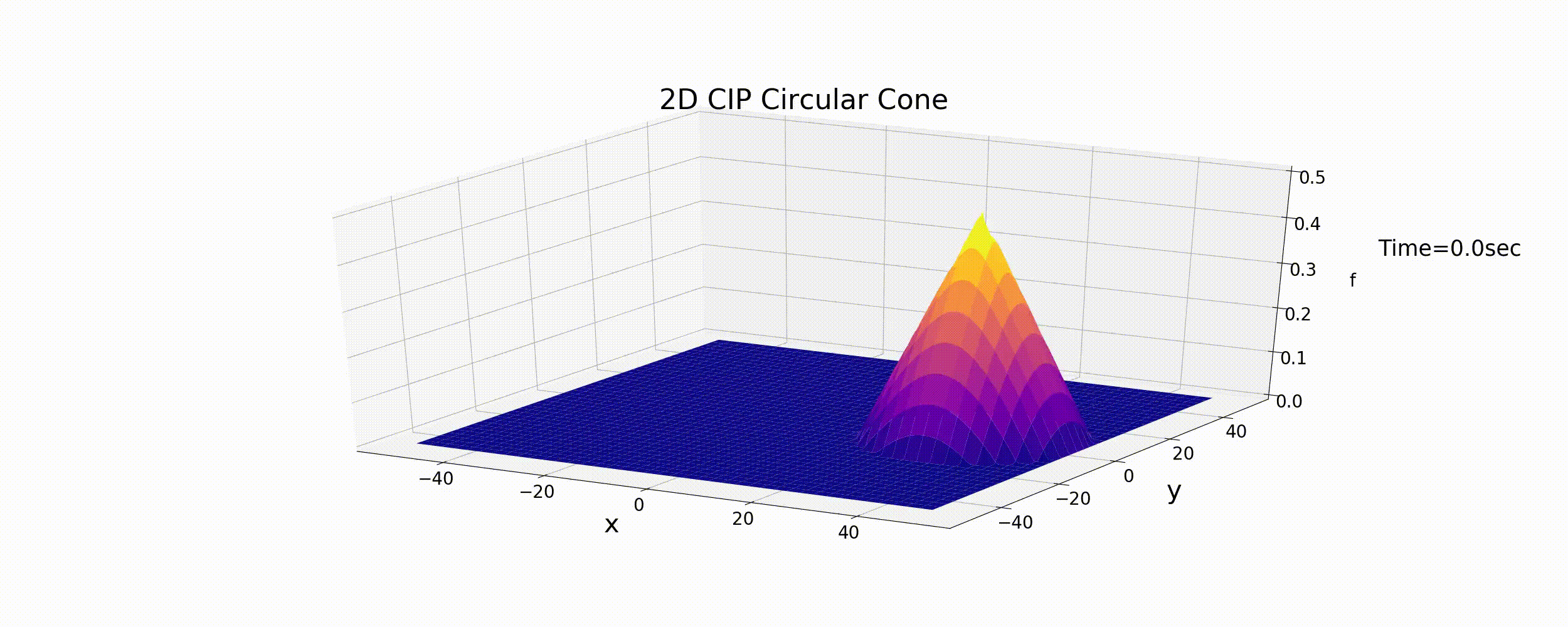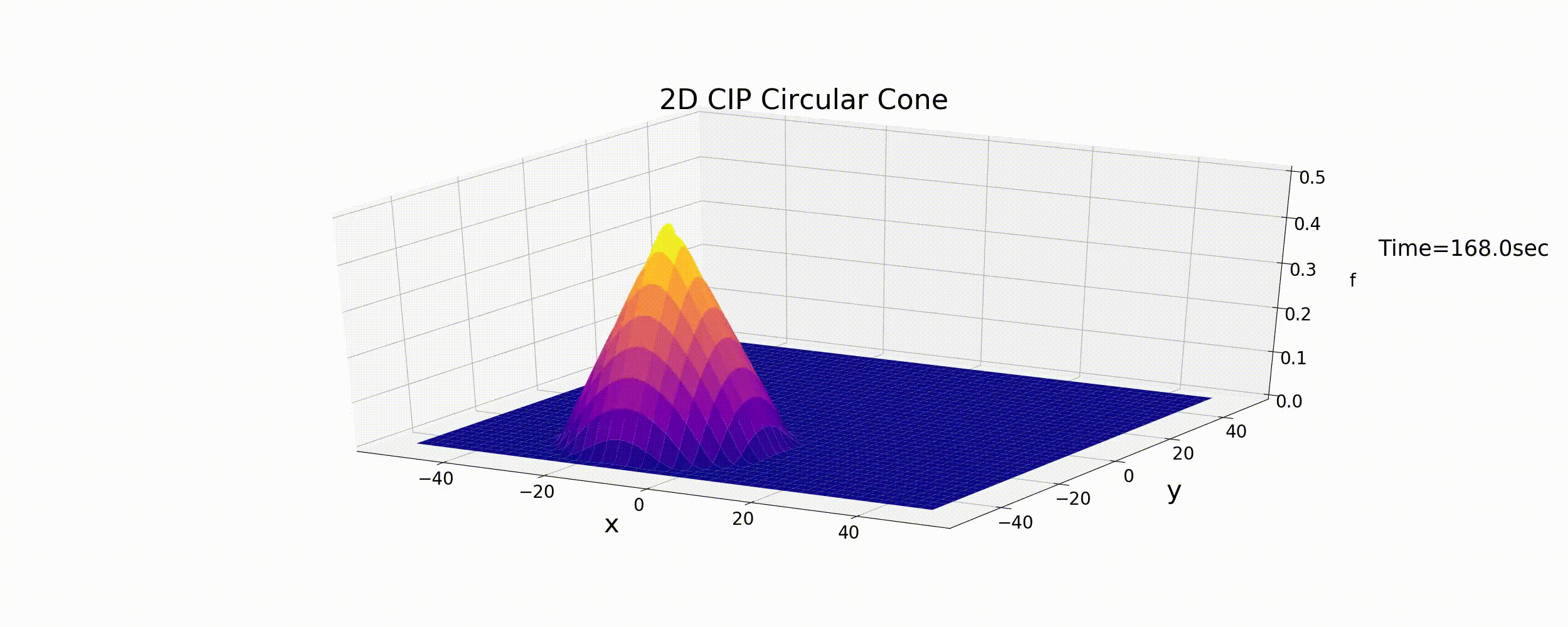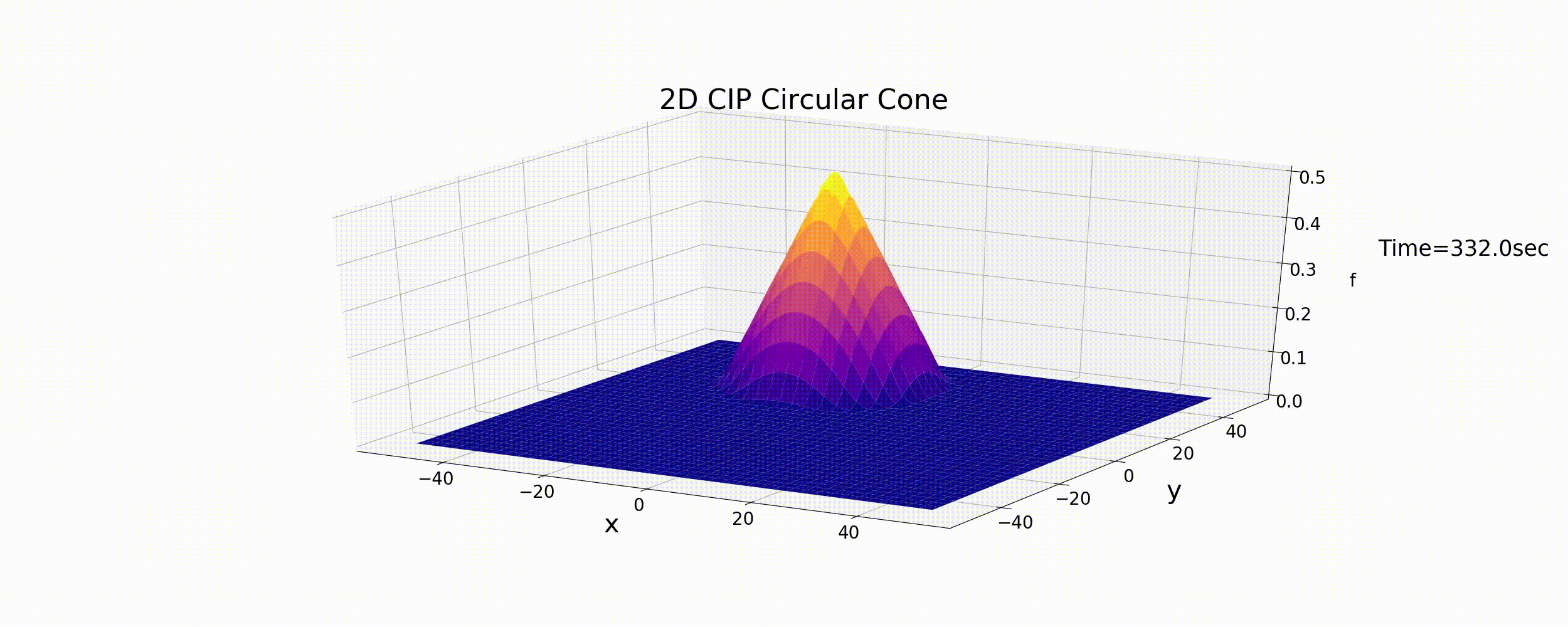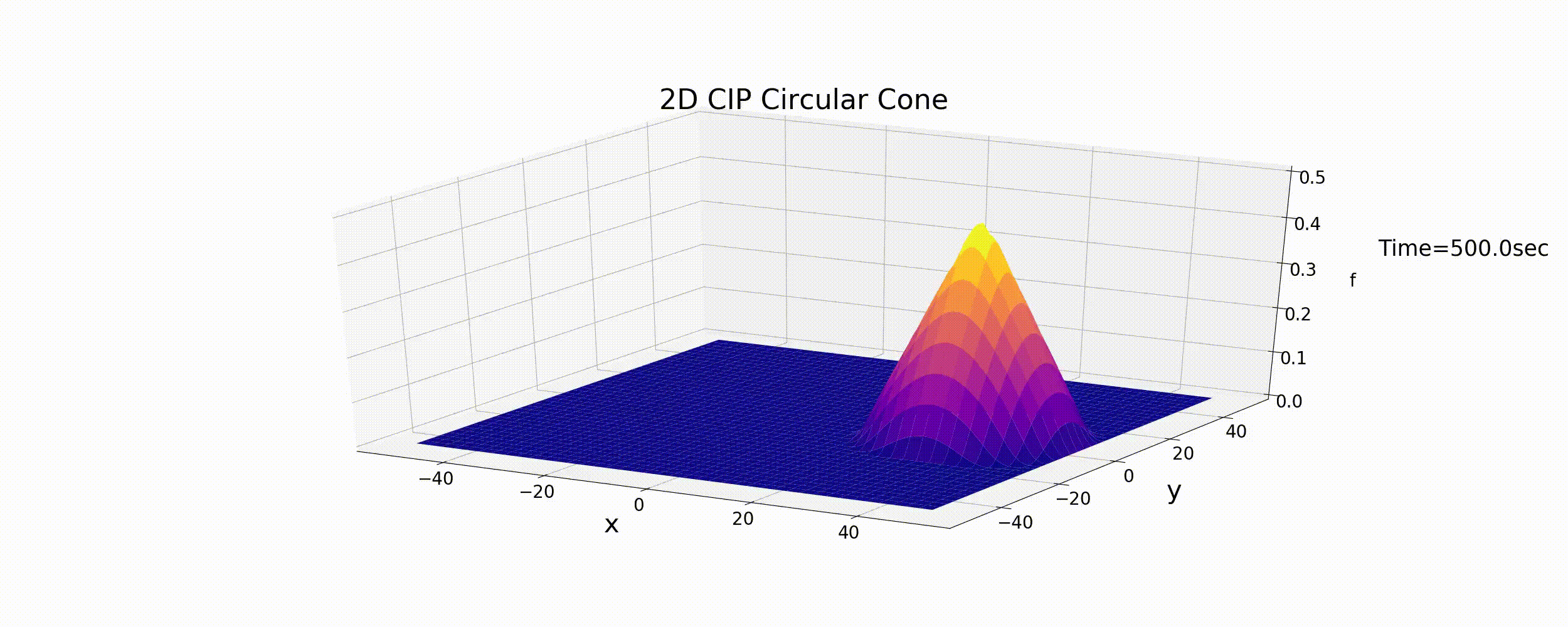
Figure 44 : 2次元移流方程式の計算結果(CIP法)

計算結果によれば，円錐形の形状はほとんど形を保ったまま円運動を続け，2次元の場合もCIP法は移流方程式の数値計算法として 高精度の計算結果が得られることが分かります．