2次元自由水面非定常流
本章では, 自由水面を有する流れの2次元非定常流れの計算法について解説します.
ここで扱う流れ場は水深方向の流速分布や鉛直方向の流速成分は考慮していないことから,
水深スケールが平面スケールに対して十分に小さい,すなわち,水深が相対的に浅い流れということで,
2次元浅水流とも呼ばれます.
2次元浅水流の基礎式は以下の連続式と,
(145) \[\frac{\partial h}{\partial t}+\frac{\partial (uh)}{\partial x}+
\frac{\partial (vh)}{\partial y}=0\]
運動方程式から構成されます.
(146) \[\frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}+
v \frac{\partial u}{\partial y}=
-g \frac{\partial H}{\partial x}
-\frac{\tau_x}{\rho h}+
\frac{\partial}{\partial x} (\nu_t \frac{\partial u}{\partial x})+
\frac{\partial}{\partial y} (\nu_t \frac{\partial u}{\partial y})\]
(147) \[\frac{\partial v}{\partial t}+u \frac{\partial v}{\partial x}+
v \frac{\partial v}{\partial y}=
-g \frac{\partial H}{\partial y}
-\frac{\tau_y}{\rho h}+
\frac{\partial}{\partial x} (\nu_t \frac{\partial v}{\partial x})+
\frac{\partial}{\partial y} (\nu_t \frac{\partial v}{\partial y})\]
ただし, \(x, y\) は互いに直交する平面座標軸, \(t\) は時間,
\(u, v\) は \(x, y\) 方向の水深平均流速, \(h\) は水深,
\(H\) は水位, \(g\) は重力加速度, \(\tau_x, \tau_y\) は \(x, y\) 方向の河床せん断力,
\(\rho\) は水の密度, \(\nu_t\) は渦動粘性係数です.
抵抗則にマニング則を用いると, 河床せん断力は下記で表されます.
(148) \[\frac{\tau_x}{\rho h}= \frac{gn^2}{h^{4/3}} u\sqrt{u^2+v^2}, \ \ \
\frac{\tau_y}{\rho h}= \frac{gn^2}{h^{4/3}} v\sqrt{u^2+v^2}\]
ただし, \(n\) はマニングの粗度係数です. (148) 式の導出についてはAppendixの 河床せん断力の表現方法について
(149) \[\nu_t = \frac{\kappa}{6} u_\ast h\]
ただし,\(u_\ast\) は摩擦速度,
(150) \[u_\ast=\sqrt{ghI_f}\]
\(I_f\) は摩擦勾配で次式で表されます.
(151) \[I_f=\frac{n^2 (u^2+v^2)}{h^{4/3}}\]
基礎式と分離解法の適用
自由水面を持つ2次元非定常流の計算では, (145) 式から水深 \(h\) を,
\(x\) 方向の運動方程式 (146) 式から \(x\) 方向の流速 \(u\) を,
\(y\) 方向の運動方程式 (146) 式から \(y\) 方向の流速 \(v\) を算出します.
なお, 水位 \(H\) は河床高 \(\eta\) が与えられた場合には
\(H=\eta+h\) で \(h\) と一意的に対応しますので \(h\) の代わりに \(H\) 未知量と考えても同じことです.
1次元の時と同じように (146) 式および (147) 式に分離解法を適用します. ほとんど
同じ形なので (146) 式の場合のみ説明します. (146) 式に \(H=\eta+h\) の関係を用いて
再記しておきます.
(152) \[{{\partial u}\over{\partial t}}+u {{\partial u}\over{\partial x}}+v{{\partial u}\over{\partial y}}
= -g \left( {{\partial h}\over{\partial x}}+{{\partial \eta}\over{\partial x}}
\right)
-{{g n_m^2 u\sqrt{u^2+v^2}}\over{h^{4/3}}}
+\nu_t \left[ {{\partial^2 u}\over{\partial x^2}}
+ {{\partial^2 u }\over{\partial y^2}} \right]\]
なお本式は拡散項も含むため,
移流項に関する部分, 圧力項と摩擦項に関する部分, および拡散項に関する部分
の3つに分離することとします.
(153) \[{{\partial u}\over{\partial t}} =
-g \displaystyle{\left( {{\partial h}\over{\partial x}} +
{{\partial \eta}\over{\partial x}} \right) }
-{{g n_m^2 u\sqrt{u^2+v^2}}\over{h^{4/3}}}\]
(154) \[{{\partial u}\over{\partial t}} =
\nu_t \displaystyle{\left[ {{\partial^2 u }\over{\partial x^2}}
+{{\partial^2 u}\over{\partial y^2}} \right] }\]
(155) \[{{\partial u}\over{\partial t}}+
u{{\partial u}\over{\partial x}}
+v{{\partial u}\over{\partial y}} = 0\]
\(n\) を時間ステップとして, (152) 式で, \(u^n \rightarrow u^{n+1}\) の計算をする
代わりに, 中間に \(\overline{u}\) と \(\widetilde{u}\) を設けて (153) 式で
\(u^n \rightarrow \overline{u}\) を, (154) 式で \(\overline{u} \rightarrow
\widetilde{u}\) を, (155) 式で \(\widetilde{u} \rightarrow u^{n+1}\)
を計算することにします. なお, (153) 式には \(h\) が含まれているため (145) 式の
連続式も同時に満たす必要があります. これを \(h^n \rightarrow \overline{h}\) と
表しておきます. これに対して (154) 式, (155) 式には \(h\) が含まれていませんので,
\(h^{n+1}\) はこの \(\overline{h}\) をそのまま用いることとします. 即ち,
(156) \[h^{n+1} = \overline{h}\]
ということです. \(v\) についてもまったく同様です. \(v\) に関する運動方程式も
以下のように分離して計算します.
(157) \[{{\partial v}\over{\partial t}} =
-g \displaystyle{\left( {{\partial h}\over{\partial y}} +
{{\partial \eta}\over{\partial y}} \right) }
-{{g n_m^2 v\sqrt{u^2+v^2}}\over{h^{4/3}}}\]
(158) \[{{\partial v}\over{\partial t}} =
\nu_t \displaystyle{\left[ {{\partial^2 v }\over{\partial x^2}}
+{{\partial^2 v}\over{\partial y^2}} \right] }\]
(159) \[\cfrac{\partial v}{\partial t}+u\cfrac{\partial v}{\partial x}
+v\cfrac{\partial v}{\partial y} = 0\]
以上を整理すると,
Table 5 2次元流れの分離解法
Phase名
変数の更新方法
使用する式
Non-Advection Phase I
\(u^n \rightarrow \overline{u}\)
\(v^n \rightarrow \overline{v}\)
\(h^n \rightarrow \overline{h} \rightarrow h^{n+1}\)
(153) , (157) , (145) , (156) 式
Non-Advection Phase II
\(\overline{u} \rightarrow \widetilde{u}\)
\(\overline{v} \rightarrow \widetilde{v}\)
(154) , (158) 式
Advection Phase
\(\widetilde{u} \rightarrow u^{n+1}\)
\(\widetilde{v} \rightarrow v^{n+1}\)
(155) , (159) 式
ということになり, 以上でCIP法を適用する準備が整いました.
Non Advection Phase I
(153) 式で \(u^n \rightarrow \overline{u}\) を,
(157) 式で \(v^n \rightarrow \overline{n}\)
を計算するので (153) 式および (157) 式を以下のように表しておきます.
(160) \[{{\overline{u}-u^n}\over{\Delta t}} =
-g \displaystyle{
\left( {{\partial \overline{h}}\over{\partial x}} +
{{\partial \eta}\over{\partial x}} \right) }
-{{g n_m^2 \overline{u} \sqrt{\overline{u}^2 +\overline{v}^2}}
\over{\overline{h}^{4/3}}}\]
(161) \[{{\overline{v}-v^n}\over{\Delta t}} =
-g \displaystyle{
\left( {{\partial \overline{h}}\over{\partial y}} +
{{\partial \eta}\over{\partial y}} \right) }
-{{g n_m^2 \overline{v} \sqrt{\overline{u}^2 +\overline{v}^2}}
\over{\overline{h}^{4/3}}}\]
これより,
(162) \[\overline{u}=
u^n - g \Delta t {{\partial \overline{h}}\over{\partial x}}
- g \Delta t {{\partial \eta}\over{\partial x}}
- g \Delta t {{n_m^2 \overline{u}\sqrt{\overline{u}^2 +\overline{v}^2}}
\over{\overline{h}^{4/3}}}\]
(163) \[\overline{v}=
v^n - g \Delta t {{\partial \overline{h}}\over{\partial y}}
- g \Delta t {{\partial \eta}\over{\partial y}}
- g \Delta t {{n_m^2 \overline{v}\sqrt{\overline{u}^2 +\overline{v}^2}}
\over{\overline{h}^{4/3}}}\]
一方, (145) 式で \(h^n \rightarrow \overline{h}\) を求めるので,
(164) \[{{\overline{h}-h^n}\over{\Delta t}} +
{{\partial}\over{\partial x}} (\overline{u} \overline{h})
+ {{\partial}\over{\partial y}} (\overline{v} \overline{h})=0\]
を満たす必要があります. 従って, (162) \(\sim\) (164)
式を連立して得られる \(\overline{h}\) , \(\overline{u}\) および
\(\overline{v}\) を求める必要があります.
CIP法で流体の計算を行う場合は一般に \(u\) , \(v\) と \(h\)
の計算点を交互に配置するスタッカード格子が用いられます.
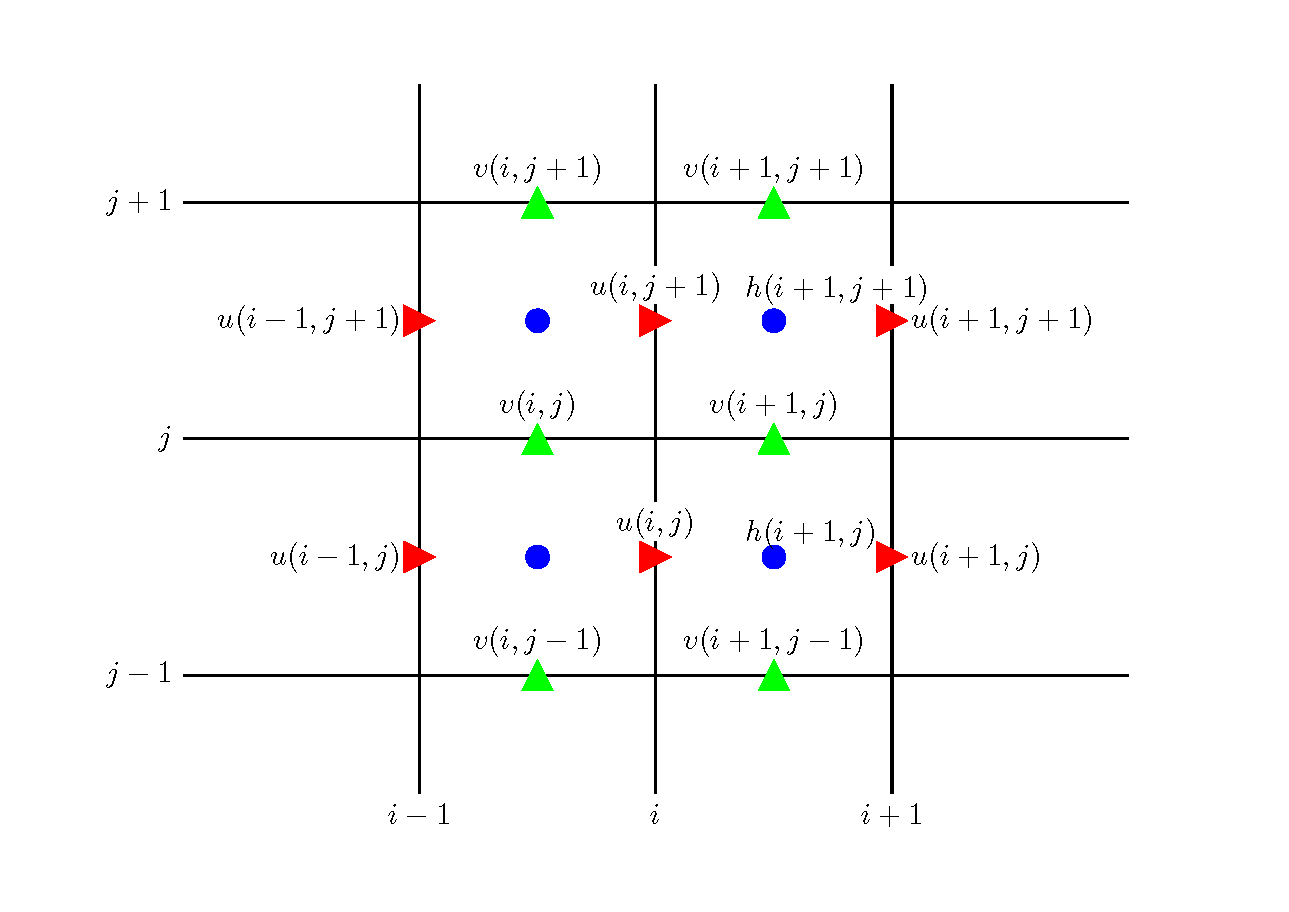
ここでは, Figure 45
Figure 45 : 計算格子の配置法
Figure 45 (162) 式を差分表示すると,
(165) \[\begin{split}\overline{u}(i,j) = &
u^n(i,j)-g\Delta t {{\overline{h}(i+1,j) - \overline{h}(i,j)}\over{\Delta x}}
-g\Delta t {{\eta(i+1,j) - \eta(i,j)}\over{\Delta x}} \\
& - g \Delta t {{n_m^2 \overline{u}(i,j)
\sqrt{\overline{u}(i,j)^2+\overline{v_{up}}^2}
}\over{\overline{h_{up}}^{4/3}}}\end{split}\]
ここで, 下付き添え字 \(_{up}\) は \(u\) の計算点における値であることを表し,
Figure 45
(166) \[\overline{v_{up}}={{\overline{v}(i,j)+\overline{v}(i,j-1)
+\overline{v}(i+1,j)+\overline{v}(i+1,j-1)}\over 4}\]
(167) \[\overline{h_{up}}={{\overline{h}(i,j)+\overline{h}(i+1,j)}\over 2}\]
となります. 同様に (163) 式を差分表示すると,
(168) \[\begin{split}\overline{v}(i,j) = &
v^n(i,j)-g\Delta t {{\overline{h}(i,j+1) - \overline{h}(i,j)}\over{\Delta y}}
-g\Delta t {{\eta(i,j+1) - \eta(i,j)}\over{\Delta y}} \\
& - g \Delta t {{n_m^2 \overline{v}(i,j)
\sqrt{\overline{u_{vp}}^2+\overline{v}(i,j)^2}
}\over{\overline{h_{vp}}^{4/3}}}\end{split}\]
となります. 下付き添え字 \(_{vp}\) は \(u\) の計算点における値であることを表し,
(169) \[\overline{u_{vp}}={{\overline{u}(i,j)+\overline{u}(i-1,j)
+\overline{u}(i,j+1)+\overline{u}(i-1,j+1)}\over 4}\]
(170) \[\overline{h_{vp}}={{\overline{h}(i,j)+\overline{h}(i,j+1)}\over 2}\]
で表されます. (165) 式および (168) 式を (164) 式の
左辺第2項および第3項に代入するために,
(171) \[\overline{q_u}=\overline{u} \overline{h}, \; \; \;
\overline{q_v}=\overline{v} \overline{h}\]
を定義し( \(q_u`nおよび :math:`q_v\) の計算点はそれぞれ
\(u\) および \(v\) と同じとする) 計算格子点の配置を考慮して,
(172) \[\overline{q_x}(i,j)=
\overline{u}(i,j) {{\overline{h}(i+1,j)+\overline{h}(i,j)}\over{2}}\]
(173) \[\overline{q_y}(i,j)=
\overline{v}(i,j) {{\overline{h}(i,j+1)+\overline{h}(i,j)}\over{2}}\]
および, \(q_x\) , \(q_y\) を用いた (164) 式の差分式
(174) \[\overline{h}(i) =h^n(i,j) + \left[
{{\overline{q_x}(i,j)-\overline{q_x}(i-1,j)}\over{\Delta x}}
+{{\overline{q_y}(i,j)-\overline{q_y}(i,j-1)}\over{\Delta y}}
\right]\Delta t\]
より \(\overline{h}\) を求めることが出来ます. ただし, (174) 式
には右辺の \(\overline{q_x}\) , \(\overline{q_y}\)
にも \(\overline{h}\) が陰的な形で含まれるため, 繰り返し計算が
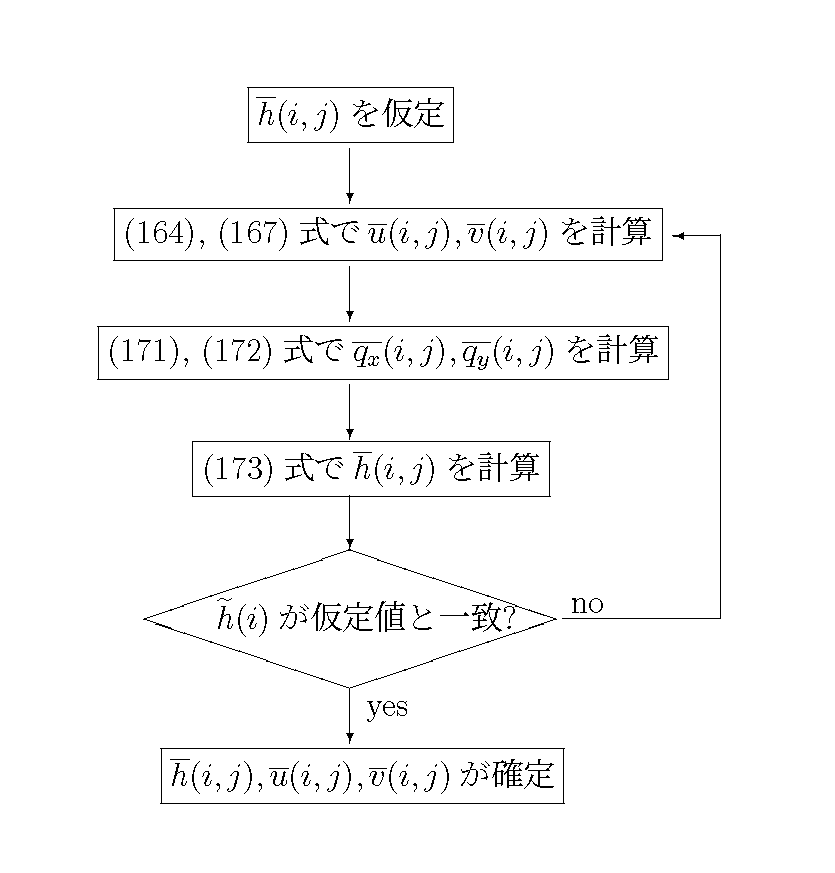
必要になります. この手順を Figure 46
Figure 46 : Non-Advection Phase I における \(\overline{h}(i,j)\) , \(\overline{u}(i,j)\) および \(\overline{v}(i,j)\) の計算手順
この繰り返し計算を通して得られる \(\overline{h}(i)\) ,
\(\overline{u}(i,j)\) および \(\widetilde{v}(i,j)\)
が Non-Advection Phase I の計算結果です.
Non-Advection Phase I における \(\overline{u}(i,j)\) と
\(\overline{v}(i,j)\) が求まった段階で, Non-Advection Phase I における
\(\displaystyle{{\partial u}\over{\partial x}}\) ,
\(\displaystyle{{\partial u}\over{\partial y}}\) ,
\(\displaystyle{{\partial v}\over{\partial x}}\) および
\(\displaystyle{{\partial v}\over{\partial y}}\)
すなわち,
\(\overline{\displaystyle{{\partial u}\over{\partial x}}}\) ,
\(\overline{\displaystyle{{\partial u}\over{\partial y}}}\) ,
\(\overline{\displaystyle{{\partial v}\over{\partial x}}}\) および
\(\overline{\displaystyle{{\partial v}\over{\partial y}}}\)
を求めておく必要があります. これは1次元の時にやったのと全く同様に以下の式で
計算できます.
(175) \[\overline{{\partial u}\over{\partial x}}(i,j)=
{{\partial u}\over{\partial x}}^n(i,j)
+{{1}\over{2\Delta t}}
\left[
\overline{u}(i+1,j)-u^n(i+1,j)-\overline{u}(i-1,j)+u^n(i-1,j)
\right]\]
(176) \[\overline{{\partial u}\over{\partial y}}(i,j)=
{{\partial u}\over{\partial y}}^n(i,j)
+{{1}\over{2\Delta t}}
\left[
\overline{u}(i,j+1)-u^n(i,j+1)-\overline{u}(i,j-1)+u^n(i,j-1)
\right]\]
(177) \[\overline{{\partial v}\over{\partial x}}(i,j)=
{{\partial v}\over{\partial x}}^n(i,j)
+{{1}\over{2\Delta t}}
\left[
\overline{v}(i+1,j)-v^n(i+1,j)-\overline{v}(i-1,j)+v^n(i-1,j)
\right]\]
(178) \[\overline{{\partial v}\over{\partial y}}(i,j)=
{{\partial v}\over{\partial y}}^n(i,j)
+{{1}\over{2\Delta t}}
\left[
\overline{v}(i,j+1)-v^n(i,j+1)-\overline{v}(i,j-1)+v^n(i,j-1)
\right]\]
Non Advection Phase II
ここでは拡散項の計算を行います.
拡散項は (154) 式および (158) 式を用いて,
\(\overline{u} \rightarrow \widetilde{u}\)
および \(\overline{v} \rightarrow \widetilde{v}\) の計算を行います.
拡散項は単純に中央差分が適用できますので, (154) 式および (158) 式
の差分表示は以下のようになります.
\[\widetilde{u}(i,j) = \overline{u}(i,j) +
\Delta t \nu_t \left[
{{\overline{u}(i+1,j)-2\overline{u}(i,j)+\overline{u}(i-1,j)}\over{\Delta x^2}}
\right.\]
(179) \[\left.
+{{\overline{u}(i,j+1)-2\overline{u}(i,j)+\overline{u}(i,j-1)}\over{\Delta y^2}}\right]\]
\[\widetilde{v}(i,j) = \overline{v}(i,j) +
\Delta t \nu_t \left[
{{\overline{v}(i+1,j)-2\overline{v}(i,j)+\overline{v}(i-1,j)}\over{\Delta x^2}}
\right.\]
(180) \[\left.
+{{\overline{v}(i,j+1)-2\overline{v}(i,j)+\overline{v}(i,j-1)}\over{\Delta y^2}}\right]\]
Advection Phase
Advection Phaseで計算する式は (155) 式と (159) 式です.
これは, 前章の2次元移流方程式( 2次元移流方程式 (123) 式で, \(f\) を \(u\) としたのが (155) 式で,
\(f\) を \(v\) としたのが (159) 式ですので前章の内容をそのまま適用できます.
ただし, 今回は \(u\) と \(v\) の計算点の配置方法が異なりますのでこの点だけ注意する
必要があります. たとえば, (135) 式にCIP法を適用する場合, 左辺第3項に現れる \(v\)
は \(u\) の計算点のものを使う必要があり, (166) 式で行ったような周辺の値からの換算が必要になります.
同様に (159) 式の左辺第2項に現れる \(u\) は \(v\) の計算点の \(u\) を使用する必要があり,
同様に (169) 式のような変換が必要になります.
これらを考慮して, Advection Phase の計算は以下のように式で行われます.
Advection Phaseの u
\[u(i,j)^{n+1}=
\left[ (a_1 X + c_1 Y + e_1) X + g_1 Y +
\overline{{\partial u}\over{\partial x}}(i,j) \right] X +\]
(181) \[\left[ (b_1 Y + d_1 X + f_1) Y +
\overline{{\partial u}\over{\partial y}}(i,j) \right] Y + \widetilde{u}(i,j)\]
ただし,
(182) \[X=-\widetilde{u}(i,j)\Delta t, \; \; \;
Y=-\widetilde{v_{up}}(i,j)\Delta t\]
(183) \[\widetilde{v_{up}}={{\widetilde{v}(i,j)+\widetilde{v}(i,j-1)
+\widetilde{v}(i+1,j)+\widetilde{v}(i+1,j-1)}\over 4}\]
なお (181) 式中の \(a_1 \sim g_1\) は前章の (138) 式で \(f\) を
\(\widetilde{u}\) に,\(f_x\) および \(f_y\) を \(u_x\) および \(u_y\) に
置き換えたものを使用します.ただし,
(184) \[u_x=\cfrac{\partial u}{\partial x}, \; \; \;
u_y=\cfrac{\partial u}{\partial x}\]
です.
Advection Phaseの v
\[v(i,j)^{n+1}=
\left[ (a_1 X + c_1 Y + e_1) X + g_1 Y +
\overline{{\partial v}\over{\partial x}}(i,j) \right] X +\]
(185) \[\left[ (b_1 Y + d_1 X + f_1) Y +
\overline{{\partial v}\over{\partial y}}(i,j) \right] Y + \widetilde{v}(i,j)\]
ただし,
(186) \[X=-\widetilde{u_{vp}}(i,j)\Delta t, \; \; \;
Y=-\widetilde{v}(i,j)\Delta tp3\]
(187) \[\widetilde{u_{vp}}={{\widetilde{u}(i,j)+\widetilde{u}(i-1,j)
+\widetilde{u}(i,j+1)+\widetilde{u}(i-1,j+1)}\over 4}\]
なお (185) 式中の \(a_1 \sim g_1\) は (138) 式で
\(f\) を \(\widetilde{v}\) に, \(f_x\) および \(f_y\) を
\(v_x\) および \(v_y\) に
置き換えたものを使用します. ただし,
(188) \[v_x=\cfrac{\partial v}{\partial x}, \; \; \;
v_y=\cfrac{\partial v}{\partial x}\]
です.
Advection Phaseにおける微分量の更新
前章の (143) 式および (144) 式を用いた微分量の更新が必要となります.
確認のためにこれらの式を再記しておきます.
(189) \[{{\partial f_x}\over{\partial t}}
+ u{{\partial f_x}\over{\partial x}}
+ v{{\partial f_x}\over{\partial y}}
= -\left( f_x {{\partial u}\over{\partial x}} +
f_y {{\partial v}\over{\partial x}} \right)\]
(190) \[{{\partial f_y}\over{\partial t}}
+ u{{\partial f_y}\over{\partial x}}
+ v{{\partial f_y}\over{\partial y}}
= -\left( f_x {{\partial u}\over{\partial y}} +
f_y {{\partial v}\over{\partial y}} \right)\]
まず, \(bibun2_21\) 式で \(f\) が \(u\) の場合を考えます.
左辺には分離解法によるCIP法を適用できますので,
2段階に分けて, CIPによる移流部分とそれ以外に分けて計算します.
たとえば, \(u\) の \(x\) 微分に関する更新を,
(191) \[\displaystyle{\overline{{\partial u}\over{\partial x}} \longrightarrow
\widehat{{\partial u}\over{\partial x}} \longrightarrow
{{\partial u}\over{\partial x}}^{n+1}}\]
と表示することにしますと, 移流部分は,
(192) \[\widehat{{\partial u}\over{\partial x}}(i,j)=
\left[3 a_1 X + 2(c_1 Y +e_1) \right] X + (d_1 Y +g_1) Y
+\overline{{\partial u}\over{\partial x}}(i,j)\]
それ以外の部分は
\[{{\partial u}\over{\partial x}}^{n+1}(i,j)=
\widehat{{\partial u}\over{\partial x}}(i,j)\]
(193) \[-\left[
\widehat{{\partial u}\over{\partial x}}(i,j)
{{\widetilde{u}(i+1,j)-\widetilde{u}(i-1,j)}\over{2 \Delta x}}
+\widehat{{\partial u}\over{\partial y}}(i,j)
{{\widetilde{v_{up}}(i+1,j)-\widetilde{v_{up}}(i-1,j)}\over{2 \Delta x}}
\right] \Delta t\]
によって計算することが出来ます( \(a_1, c_1, e_1, d_1, g_1\)
は前節を参照願います).
同様に, \(u\) の \(y\) に関する微分量の更新は,
(194) \[\widehat{{\partial u}\over{\partial y}}(i,j)=
\left[3 b_1 Y + 2(d_1 X +f_1) \right] Y + (c_1 X +g_1) X
+\overline{{\partial u}\over{\partial y}}(i,j)\]
\[{{\partial u}\over{\partial y}}^{n+1}(i,j)=
\widehat{{\partial u}\over{\partial y}}(i,j)\]
(195) \[-\left[
\widehat{{\partial u}\over{\partial x}}(i,j)
{{\widetilde{u}(i,j+1)-\widetilde{u}(i,j-1)}\over{2 \Delta y}}
+\widehat{{\partial u}\over{\partial y}}(i,j)
{{\widetilde{v_{up}}(i,j+1)-\widetilde{v_{up}}(i,j-1)}\over{2 \Delta y}}
\right] \Delta t\]
によって計算することが出来ます. なお,
(193) 式および (195) 式右辺第2項と第3項の
\(\displaystyle{\widehat{{\partial u}\over{\partial x}}}\) および
\(\displaystyle{\widehat{{\partial u}\over{\partial y}}}\)
は, それぞれ直前の (192) 式や (194) 式で計算されるものを用いるよりは,
別途, \(\widetilde{u}\) を用いて計算し直したほうが計算の安定性が高まる
ことが知られております.
この場合, (193) 式と (195) 式の代わりに以下の式を用いるということになります.
\[{{\partial u}\over{\partial x}}^{n+1}(i,j)=
\widehat{{\partial u}\over{\partial x}}(i,j)
-\left\{
{{[\widetilde{u}(i+1,j)-\widetilde{u}(i-1,j)]}\over{2 \Delta x}}
{{[\widetilde{u}(i+1,j)-\widetilde{u}(i-1,j)]}\over{2 \Delta x}}
\right.\]
(196) \[\left. +
{{[\widetilde{u}(i,j+1)-\widetilde{u}(i,j-1)]}\over{2 \Delta y}}
{{[\widetilde{v_{up}}(i+1,j)-\widetilde{v_{up}}(i-1,j)]}\over{2 \Delta x}}
\right\} \Delta t\]
\[{{\partial u}\over{\partial y}}^{n+1}(i,j)=
\widehat{{\partial u}\over{\partial y}}(i,j)
-\left\{
{{[\widetilde{u}(i+1,j)-\widetilde{u}(i-1,j)]}\over{2 \Delta x}}
{{[\widetilde{u}(i,j+1)-\widetilde{u}(i,j-1)]}\over{2 \Delta y}}
\right.\]
(197) \[\left. +
{{[\widetilde{u}(i,j+1)-\widetilde{u}(i,j-1)]}\over{2 \Delta y}}
{{[\widetilde{v_{up}}(i,j+1)-\widetilde{v_{up}}(i,j-1)]}\over{2 \Delta y}}
\right\} \Delta t\]
演習問題(7)
Advection Phaseにおける \(\displaystyle{\cfrac{\partial v}{\partial x}}\) , \(\displaystyle{\cfrac{\partial v}{\partial y}}\) の計算法を説明してください
Pythonコードと計算例
Pythonコード
以上で説明した2次元非定常自由水面流れの計算用Pythonコードをこちらに示します.
https://github.com/YasuShimizu/2DH_Python
計算条件に関するパラメーターはこのレポジトリ内のconfig.ymlに記述します.
なお,このコードでは本章で説明した以外に水路側壁(河岸)の摩擦を考慮出来るようにして
あります.水路側壁(河岸)の摩擦の計算方法に関する解説を,Appendixの 河岸(側壁)摩擦抵抗について
以下に示す計算例では,障害物お個数が1個で \(x\) 方向に \(i=\) 10~14番目のセル,
\(y\) 方向に \(j=\) 6~14番目のセルが障害物であるという設定になってます.
これによって,直線水路の上流側中央部に長方形の障害物があって,これによって流れが分断され
後方に間欠的なカルマン渦が発生する様子が計算されています.
Figure 47 : 計算結果のアニメーション(流速ベクトルと流速による渦度)
NaysMiniについて
NaysMini は,本章で解説した
直交座標2次元モデルをiRICのGUIと連動させて使用するためのソルバで, ソースコードもすべて公開
されております.
NaysMiniのマニュアル も公開されておりますので,
併せてご覧ください.