2次元流れ基礎方程式のs-n座標への変換
\(s-n\) 座標を直交曲線座標とします. \(s-n\) 座標において, \(s\) 軸は任意の曲線, \(n\) 軸は s 軸に直交する直線座標軸とします.
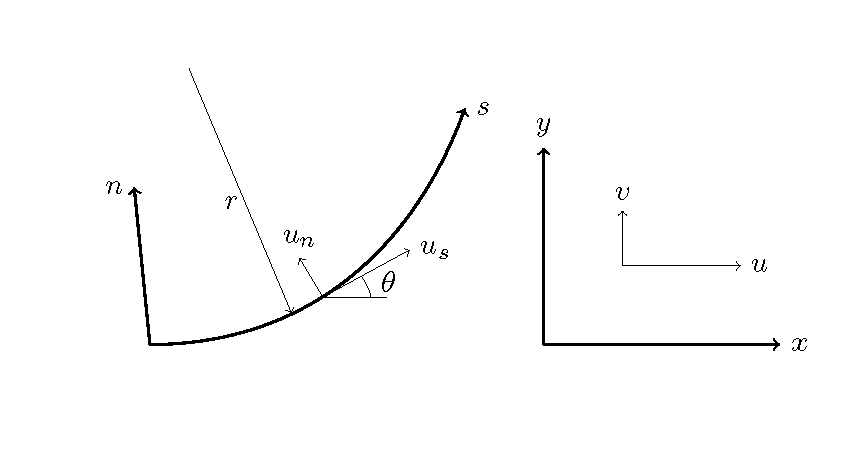
Figure 152 : \(x-y\) 座標と, \(s-n\) 座標
Figure 152 に示すように, \(x-y\) 座標における \(x\) 軸方向の流速を u, \(y\) 軸方向の流速を \(v\), \(s-n\) 座標における \(s\) 軸方向の流速を u_s, \(n\) 軸方向の流速を \(u_n\) とします. また, \(s\) 軸と \(x\) 軸の角度を \(\theta\), \(s\) 軸の曲率半径を \(r\) とします.
Figure 152 に示すように, \(s\) 軸のプラス方向に向かって \(\theta\) が増えていくような曲がりの時の
曲率半径で \(r\) が正になるような定義とします.
曲率の定義より,
(391)\[r d\theta = ds, \; \; \cfrac{\partial \theta}{\partial s}= \cfrac{1}{r}, \; \;
\cfrac{\partial \theta}{\partial n}=0\]
\(u,v\) と \(u, v\) は下記の関係となります.
(392)\[\begin{split}u=u_s \cos \theta - u_n \sin \theta \\
v=u_s \sin \theta + u_n \cos \theta\end{split}\]
(393)\[\begin{split}u_s=u \cos \theta + v \sin \theta \\
u_n=-u \sin \theta + v \cos \theta\end{split}\]
また,各偏微分は下記のような関係になります.
(394)\[\begin{split}\left( \begin{array}{c}
\cfrac{\partial}{\partial x} \\
\\
\cfrac{\partial}{\partial y}
\end{array} \right)
=
\left( \begin{array}{cc}
\cos{\theta} & -\sin{\theta} \\
\\
\sin{\theta} & \cos{\theta}
\end{array} \right)
\left( \begin{array}{c}
\cfrac{\partial}{\partial s} \\
\\
\cfrac{\partial}{\partial n}
\end{array} \right)\end{split}\]
(395)\[\begin{split}\left( \begin{array}{c}
\displaystyle{{\partial}\over{\partial s}} \\
\\
\displaystyle{{\partial}\over{\partial n}}
\end{array} \right)
=
\left( \begin{array}{cc}
\cos{\theta} & \sin{\theta} \\
\\
-\sin{\theta} &
\cos{\theta}
\end{array} \right)
\left( \begin{array}{c}
\displaystyle{{\partial}\over{\partial x}} \\
\\
\displaystyle{{\partial}\over{\partial y}}
\end{array} \right)\end{split}\]
また,
(396)\[\cfrac{\partial s}{\partial x}=\cos \theta, \; \;
\cfrac{\partial s}{\partial y}=\sin \theta, \; \;
\cfrac{\partial n}{\partial x}=-\sin \theta, \; \;
\cfrac{\partial n}{\partial y}=\cos \theta\]
連続式
(397)\[\cfrac{\partial h}{\partial t}
+\cfrac{\partial (hu)}{\partial x}
+\cfrac{\partial (hv)}{\partial y}=0\]
(398)\[\cfrac{\partial h}{\partial t}
+\cfrac{\partial}{\partial x}
\left\{ h(u_s \cos \theta - u_n \sin \theta) \right\}
+\cfrac{\partial}{\partial y}
\left\{ h(u_s \sin \theta + u_n \cos \theta) \right\}=0\]
(399)\[\begin{split}\cfrac{\partial h}{\partial t}
+\cos \theta \cfrac{\partial}{\partial s}
\left\{ h(u_s \cos \theta - u_n \sin \theta) \right\}
-\sin \theta \cfrac{\partial}{\partial n}
\left\{ h(u_s \cos \theta - u_n \sin \theta) \right\} \\
+\sin \theta \cfrac{\partial}{\partial s}
\left\{ h(u_s \sin \theta + u_n \cos \theta) \right\}
+\cos \theta \cfrac{\partial}{\partial n}
\left\{ h(u_s \sin \theta + u_n \cos \theta) \right\}=0\end{split}\]
(400)\[\begin{split}\cfrac{\partial h}{\partial t}
+\cos \theta \left\{
\cos\theta \cfrac{\partial(h u_s)}{\partial s}+h u_s \cfrac{\partial \cos \theta}{\partial s}
-\sin\theta \cfrac{\partial(h u_n)}{\partial s}-h u_n \cfrac{\partial \sin \theta}{\partial s}
\right\} \\
-\sin \theta \left\{
\cos\theta \cfrac{\partial(h u_s)}{\partial n}+h u_s \cancelto{0}{\cfrac{\partial \cos \theta}{\partial n}}
-\sin\theta \cfrac{\partial(h u_n)}{\partial n}-h u_n \cancelto{0}{\cfrac{\partial \sin \theta}{\partial n}}
\right\} \\
+\sin \theta \left\{
\sin\theta \cfrac{\partial(h u_s)}{\partial s}+h u_s \cfrac{\partial \sin \theta}{\partial s}
+\cos\theta \cfrac{\partial(h u_n)}{\partial s}+h u_n \cfrac{\partial \cos \theta}{\partial s}
\right\} \\
+\cos \theta \left\{
\sin\theta \cfrac{\partial(h u_s)}{\partial n}+h u_s \cancelto{0}{\cfrac{\partial \sin \theta}{\partial n}}
+\cos\theta \cfrac{\partial(h u_n)}{\partial n}+h u_n \cancelto{0}{\cfrac{\partial \cos \theta}{\partial n}}
\right\}\end{split}\]
(401)\[\begin{split}\cfrac{\partial h}{\partial t}
+\cos^2\theta\cfrac{\partial(hu_s)}{\partial s} \cancel{-\cos\theta\sin\theta hu_s\cfrac{\partial\theta}{\partial s}}
\cancel{-\cos\theta\sin\theta\cfrac{\partial(hu_n)}{\partial s}}-\cos^2\theta hu_n\cfrac{\partial\theta}{\partial s} \\
\cancel{-\sin\theta\cos\theta\cfrac{\partial(hu_s)}{\partial n}}
+\sin^2\theta\cfrac{\partial(hu_n)}{\partial n} \\
+\sin^2\theta\cfrac{\partial(hu_s)}{\partial s} +\cancel{\sin\theta\cos\theta hu_s\cfrac{\partial\theta}{\partial s}}
\cancel{+\sin\theta\cos\theta\cfrac{\partial(hu_n)}{\partial s}}-\sin^2\theta hu_n\cfrac{\partial\theta}{\partial s} \\
\cancel{+\cos\theta\sin\theta\cfrac{\partial(hu_s)}{\partial n}}
+\cos^2\theta\cfrac{\partial(hu_n)}{\partial n}\end{split}\]
(402)\[\begin{split}\cfrac{\partial h}{\partial t}
+(\cos^2\theta+\sin^2\theta)\cfrac{\partial(hu_s)}{\partial s}
-(\cos^2\theta+\sin^2\theta)hu_n\cfrac{\partial\theta}{\partial s} \\
+(\cos^2\theta+\sin^2\theta)\cfrac{\partial(hu_n)}{\partial n} =0\end{split}\]
(403)\[\cfrac{\partial h}{\partial t}
+\cfrac{\partial(hu_s)}{\partial s}-\cfrac{hu_n}{r}
+\cfrac{\partial(hu_n)}{\partial n} =0\]
ここで,
(404)\[\begin{split}\cfrac{\partial(rhu_n)}{\partial n}=r\cfrac{\partial(hu_n)}{\partial n}
+hu_n\cfrac{\partial r}{\partial n} \\
= r\cfrac{\partial(hu_n)}{\partial n}-hu_n\end{split}\]
なので,最終的に \(s-n\) 座標における連続式は,
(405)\[\cfrac{\partial h}{\partial t}
+\cfrac{\partial(hu_s)}{\partial s}
+\cfrac{1}{r}\cfrac{\partial(rhu_n)}{\partial n} =0\]
となります.
運動方程式
\(x-y\) 座標における運動方程式を再記します.
(406)\[\frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}+
v \frac{\partial u}{\partial y}=
-g \frac{\partial H}{\partial x}
-\frac{\tau_x}{\rho h}+D_x\]
(407)\[\frac{\partial v}{\partial t}+u \frac{\partial v}{\partial x}+
v \frac{\partial v}{\partial y}=
-g \frac{\partial H}{\partial y}
-\frac{\tau_y}{\rho h}+D_y\]
ただし, \(x, y\) は互いに直交する平面座標軸, \(t\) は時間,
\(u, v\) は \(x, y\) 方向の水深平均流速, \(h\) は水深,
\(H\) は水位, \(g\) は重力加速度, \(\tau_x, \tau_y\) は \(x, y\) 方向の河床せん断力,
\(\rho\) は水の密度, \(D_x, D_y\) は \(x, y\) 方向の拡散項です.
(406) 式, (407) 式を以下のように表します.
(408)\[\begin{split}A_x = P_x + F_x + D_x\\
A_y = P_y + F_y + D_x\end{split}\]
ただし, \(A_x, A_y, P_x, P_y, F_x, F_y, D_x, D_y\) はそれぞれ,
\(x, y\) 方向の移流項(加速度項), 圧力勾配項, 摩擦項および拡散項です.
また, これらの添え字を \(s,n\) に変えたものを \(s,n\) 軸方向のそれぞれ
各項とします.
\(x, y\) 軸方向の加速度(移流項)
(409)\[\begin{split}A_x = {{\partial u}\over{\partial t}}
+u{{\partial u}\over{\partial x}}
+v{{\partial u}\over{\partial y}}
={{\partial u}\over{\partial t}}
+u\left(
\cos\theta{{\partial u}\over{\partial s}}
-\sin\theta{{\partial u}\over{\partial n}} \right)
+v\left(
\sin\theta{{\partial u}\over{\partial s}}
+\cos\theta{{\partial u}\over{\partial n}} \right) \\
={{\partial u}\over{\partial t}}+
{{\partial u}\over{\partial s}}
\underbrace{(u\cos\theta+v\sin\theta)}_{u_s}
+{{\partial u}\over{\partial n}}
\underbrace{(-u\sin\theta+v\cos\theta)}_{u_n}
={{\partial u}\over{\partial t}}+
u_s{{\partial u}\over{\partial s}}
+u_n{{\partial u}\over{\partial n}}\end{split}\]
(410)\[\begin{split}A_y = {{\partial v}\over{\partial t}}
+u{{\partial v}\over{\partial x}}
+v{{\partial v}\over{\partial y}}
={{\partial u}\over{\partial t}}
+u\left(
\cos\theta{{\partial v}\over{\partial s}}
-\sin\theta{{\partial v}\over{\partial n}} \right)
+v\left(
\sin\theta{{\partial v}\over{\partial s}}
+\cos\theta{{\partial v}\over{\partial n}} \right) \\
={{\partial v}\over{\partial t}}+
{{\partial v}\over{\partial s}}
\underbrace{(u\cos\theta+v\sin\theta)}_{u_s}
+{{\partial v}\over{\partial n}}
\underbrace{(-u\sin\theta+v\cos\theta)}_{u_n}
={{\partial u}\over{\partial t}}+
u_s{{\partial v}\over{\partial s}}
+u_n{{\partial v}\over{\partial n}}\end{split}\]
\(s\) 軸方向の加速度(移流項)
(411)\[ \begin{align}\begin{aligned}A_s = & A_x\cos\theta+A_y\sin\theta
=\left(
{{\partial u}\over{\partial t}}+
u_s{{\partial u}\over{\partial s}}
+u_n{{\partial u}\over{\partial n}}
\right)\cos\theta+
\left(
{{\partial v}\over{\partial t}}+
u_s{{\partial v}\over{\partial s}}
+u_n{{\partial v}\over{\partial n}}
\right)\sin\theta\\= &\cos\theta{{\partial u}\over{\partial t}}
+
\cos\theta u_s {{\partial}\over{\partial s}}
(u_s\cos\theta-u_n\sin\theta)
+\cos\theta u_n{{\partial}\over{\partial n}}
(u_s\cos\theta-u_n\sin\theta)\\& +\sin\theta{{\partial v}\over{\partial t}}
+\sin\theta u_s {{\partial}\over{\partial s}}
(u_s\sin\theta+u_n\cos\theta)
+\sin\theta u_n {{\partial}\over{\partial n}}
(u_s\sin\theta+u_n\cos\theta)\\= & {{\partial u_s}\over{\partial t}}
+u_s\cos^2\theta {{\partial u_s}\over{\partial s}}
+u_s^2\cos\theta{{\partial(\cos\theta)}\over{\partial s}}
-u_s\sin\theta \cos\theta{{\partial u_n}\over{\partial s}}
-u_s u_n\cos\theta{{\partial(\sin\theta)}\over{\partial s}}\\& +u_n\cos^2\theta {{\partial u_s}\over{\partial n}}
+u_s u_n\cos\theta{{\partial(\cos\theta)}\over{\partial n}}
-u_n\sin\theta \cos\theta{{\partial u_n}\over{\partial n}}
-u_n^2\cos\theta{{\partial(\sin\theta)}\over{\partial n}}\\& +u_s\sin^2\theta {{\partial u_s}\over{\partial s}}
+u_s^2\sin\theta{{\partial(\sin\theta)}\over{\partial s}}
+u_s\sin\theta \cos\theta{{\partial u_n}\over{\partial s}}
+u_s u_n\sin\theta{{\partial(\cos\theta)}\over{\partial s}}\\& +u_n\sin^2\theta {{\partial u_s}\over{\partial n}}
+u_s u_n\sin\theta{{\partial(\sin\theta)}\over{\partial n}}
+u_n\sin\theta \cos\theta{{\partial u_n}\over{\partial n}}
+u_n^2\sin\theta{{\partial(\cos\theta)}\over{\partial n}}\\= & {{\partial u_s}\over{\partial t}}
+u_s{{\partial u_s}\over{\partial s}}
+u_n{{\partial u_s}\over{\partial n}}\\& +u_s^2\cos\theta{{\partial(\cos\theta)}\over{\partial s}}
-u_s u_n\cos\theta{{\partial(\sin\theta)}\over{\partial s}}
+u_s u_n\cos\theta{{\partial(\cos\theta)}\over{\partial n}}
-u_n^2\cos\theta{{\partial(\sin\theta)}\over{\partial n}}\\& +u_s^2\sin\theta{{\partial(\sin\theta)}\over{\partial s}}
+u_s u_n\sin\theta{{\partial(\cos\theta)}\over{\partial s}}
+u_s u_n\sin\theta{{\partial(\sin\theta)}\over{\partial n}}
+u_n^2\sin\theta{{\partial(\cos\theta)}\over{\partial n}}\\= & {{\partial u_s}\over{\partial t}}
+u_s{{\partial u_s}\over{\partial s}}
+u_n{{\partial u_s}\over{\partial n}}
+u_s^2\left\{\sin\theta{{\partial(\sin\theta)}\over{\partial s}}
+\cos\theta{{\partial(\cos\theta)}\over{\partial s}}\right\}\\& +u_s u_n\left\{
\cos\theta{{\partial(\cos\theta)}\over{\partial n}}
-\cos\theta{{\partial(\sin\theta)}\over{\partial s}}
+\sin\theta{{\partial(\cos\theta)}\over{\partial s}}
+\sin\theta{{\partial(\sin\theta)}\over{\partial n}}
\right\}\\& +u_n^2\left\{
\sin\theta{{\partial(\cos\theta)}\over{\partial n}}
-\cos\theta{{\partial(\sin\theta)}\over{\partial n}}
\right\}\end{aligned}\end{align} \]
ここで,
(412)\[\sin\theta{{\partial(\sin\theta)}\over{\partial s}}
+\cos\theta{{\partial(\cos\theta)}\over{\partial s}}
=\sin\theta\cos\theta{{\partial \theta}\over{\partial s}}
-\cos\theta\sin\theta{{\partial \theta}\over{\partial s}}=0\]
(413)\[ \begin{align}\begin{aligned}& \cos\theta{{\partial(\cos\theta)}\over{\partial n}}
-\cos\theta{{\partial(\sin\theta)}\over{\partial s}}
+\sin\theta{{\partial(\cos\theta)}\over{\partial s}}
+\sin\theta{{\partial(\sin\theta)}\over{\partial n}}\\= & \cancel{-\cos\theta\sin\theta{{\partial \theta}\over{\partial n}}}
-\cos^2\theta{{\partial \theta}\over{\partial s}}
-\sin^2\theta{{\partial \theta}\over{\partial s}}
\cancel{+\sin\theta\cos\theta{{\partial \theta}\over{\partial n}}}\\= &-\left(\cos^2\theta+\sin^2\theta\right){{\partial \theta}\over{\partial s}}\\= &-{{\partial \theta}\over{\partial s}}=-{1 \over r}\end{aligned}\end{align} \]
また,
(414)\[\sin\theta{{\partial(\cos\theta)}\over{\partial n}}
-\cos\theta{{\partial(\sin\theta)}\over{\partial n}}=
-\sin^2\theta{{\partial \theta}\over{\partial n}}
-\cos^2\theta{{\partial \theta}\over{\partial n}}
=-{{\partial \theta}\over{\partial n}}=0\]
なので, \(s\) 軸方向の移流項は次式のようになります.
(415)\[A_s=
{{\partial u_s}\over{\partial t}}
+u_s{{\partial u_s}\over{\partial s}}
+u_n{{\partial u_s}\over{\partial n}}
-{{u_s u_n}\over{r}}\]
\(n\) 軸方向の加速度(移流項)
(416)\[ \begin{align}\begin{aligned}A_n = & -A_x\sin\theta+A_y\cos\theta
\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad\\= & -\left(
{{\partial u_x}\over{\partial t}}+
u_s{{\partial u_x}\over{\partial s}}
+u_n{{\partial u_x}\over{\partial n}}
\right)\sin\theta+
\left(
{{\partial u_y}\over{\partial t}}+
u_s{{\partial u_y}\over{\partial s}}
+u_n{{\partial u_y}\over{\partial n}}
\right)\cos\theta\\= & {{\partial u_n}\over{\partial t}}
-\sin\theta u_s {{\partial}\over{\partial s}}
(u_s\cos\theta-u_n\sin\theta)
-\sin\theta u_n{{\partial}\over{\partial n}}
(u_s\cos\theta-u_n\sin\theta)\\& +\cos\theta u_s {{\partial}\over{\partial s}}
(u_s\sin\theta+u_n\cos\theta)
+\cos\theta u_n {{\partial}\over{\partial n}}
(u_s\sin\theta+u_n\cos\theta)\\= & {{\partial u_n}\over{\partial t}}
-u_s\sin\theta\cos\theta {{\partial u_s}\over{\partial s}}
-u_s^2\sin\theta{{\partial(\cos\theta)}\over{\partial s}}
+u_s\sin^2\theta {{\partial u_n}\over{\partial s}}
+u_s u_n\sin\theta{{\partial(\sin\theta)}\over{\partial s}}\\& -u_n\sin\theta\cos\theta {{\partial u_s}\over{\partial n}}
-u_s u_n\sin\theta{{\partial(\cos\theta)}\over{\partial n}}
+u_n\sin^2\theta {{\partial u_n}\over{\partial n}}
+u_n^2\sin\theta{{\partial(\sin\theta)}\over{\partial n}}\\& +u_s\cos\theta\sin\theta {{\partial u_s}\over{\partial s}}
+u_s^2\cos\theta{{\partial(\sin\theta)}\over{\partial s}}
+u_s\cos^2\theta{{\partial u_n}\over{\partial s}}
+u_s u_n\cos\theta{{\partial(\cos\theta)}\over{\partial s}}\\& +u_n\sin\theta\cos\theta {{\partial u_s}\over{\partial n}}
+u_s u_n\cos\theta{{\partial(\sin\theta)}\over{\partial n}}
+u_n\cos^2\theta{{\partial u_n}\over{\partial n}}
+u_n^2\cos\theta{{\partial(\cos\theta)}\over{\partial n}}\\= & {{\partial u_n}\over{\partial t}}
+u_s{{\partial u_n}\over{\partial s}}
+u_n{{\partial u_n}\over{\partial n}}\\& -u_s^2\sin\theta{{\partial(\cos\theta)}\over{\partial s}}
+u_s u_n\sin\theta{{\partial(\sin\theta)}\over{\partial s}}
-u_s u_n\sin\theta{{\partial(\cos\theta)}\over{\partial n}}
+u_n^2\sin\theta{{\partial(\sin\theta)}\over{\partial n}}\\& +u_s^2\cos\theta{{\partial(\sin\theta)}\over{\partial s}}
+u_s u_n\cos\theta{{\partial(\cos\theta)}\over{\partial s}}
+u_s u_n\cos\theta{{\partial(\sin\theta)}\over{\partial n}}
+u_n^2\cos\theta{{\partial(\cos\theta)}\over{\partial n}}\\= & {{\partial u_n}\over{\partial t}}
+u_s{{\partial u_n}\over{\partial s}}
+u_n{{\partial u_n}\over{\partial n}}
+u_s^2\left\{-\sin\theta{{\partial(\cos\theta)}\over{\partial s}}
+\cos\theta{{\partial(\sin\theta)}\over{\partial s}}\right\}\\& +u_s u_n\left\{
\sin\theta{{\partial(\sin\theta)}\over{\partial s}}
-\sin\theta{{\partial(\cos\theta)}\over{\partial n}}
+\cos\theta{{\partial(\cos\theta)}\over{\partial s}}
+\cos\theta{{\partial(\sin\theta)}\over{\partial n}}
\right\}\\& +u_n^2\left\{
\sin\theta{{\partial(\sin\theta)}\over{\partial n}}
+\cos\theta{{\partial(\cos\theta)}\over{\partial n}}
\right\}\end{aligned}\end{align} \]
ここで,
(417)\[-\sin\theta{{\partial(\cos\theta)}\over{\partial s}}
+\cos\theta{{\partial(\sin\theta)}\over{\partial s}}
=\sin^2\theta{{\partial \theta}\over{\partial s}}
+\cos^2\theta{{\partial \theta}\over{\partial s}}={1 \over r}\]
(418)\[ \begin{align}\begin{aligned}& \sin\theta{{\partial(\sin\theta)}\over{\partial s}}
-\sin\theta{{\partial(\cos\theta)}\over{\partial n}}
+\cos\theta{{\partial(\cos\theta)}\over{\partial s}}
+\cos\theta{{\partial(\sin\theta)}\over{\partial n}}\\= & \cancel{\sin\theta\cos\theta{{\partial \theta}\over{\partial s}}}
+\sin^2\theta{{\partial \theta}\over{\partial n}}
\cancel{-\sin\theta\cos\theta{{\partial \theta}\over{\partial s}}}
+\cos^2\theta{{\partial \theta}\over{\partial n}}\\= & {{\partial \theta}\over{\partial n}}=0\end{aligned}\end{align} \]
(419)\[\sin\theta{{\partial(\sin\theta)}\over{\partial n}}
+\cos\theta{{\partial(\cos\theta)}\over{\partial n}}=
\sin\theta\cos\theta{{\partial \theta}\over{\partial n}}
-\sin\theta\cos\theta{{\partial \theta}\over{\partial n}}
=0\]
なので, \(n\) 軸方向の移流項は次式のようになります.
(420)\[A_n=
{{\partial u_n}\over{\partial t}}
+u_s{{\partial u_n}\over{\partial s}}
+u_n{{\partial u_n}\over{\partial n}}
+{{u_s^2}\over{r}}\]
圧力項
\(x,y\) 軸方向の圧力勾配は,
(421)\[ \begin{align}\begin{aligned}P_x= & -g\cfrac{\partial H}{\partial x}
=-g\left(\cos\theta\cfrac{\partial H}{\partial s}
-\sin\theta\cfrac{\partial H}{\partial n}
\right)\\P_y= & -g\cfrac{\partial H}{\partial y}
=-g\left(\sin\theta\cfrac{\partial H}{\partial s}
+\cos\theta\cfrac{\partial H}{\partial n}
\right)\end{aligned}\end{align} \]
これを, \(s, n\) 軸方向の圧力勾配, \(P_s, P_n\) に変換します.
(422)\[\begin{split}P_s= & P_x \cos\theta+P_y \sin\theta \\
= & \cos\theta\left\{
-g\left(\cos\theta\cfrac{\partial H}{\partial s}
-\sin\theta\cfrac{\partial H}{\partial n}
\right)
\right\}
+\sin\theta\left\{
-g\left(\sin\theta\cfrac{\partial H}{\partial s}
+\cos\theta\cfrac{\partial H}{\partial n}
\right)
\right\} \\
= & g\left(
-\cos^2\theta\cfrac{\partial H}{\partial s}
\cancel{+\cos\theta\sin\theta\cfrac{\partial H}{\partial n}}
-\sin^2\theta\cfrac{\partial H}{\partial s}
\cancel{-\cos\theta\sin\theta\cfrac{\partial H}{\partial n}}
\right) \\
= & -g\cfrac{\partial H}{\partial s}\end{split}\]
(423)\[\begin{split}P_n= & -P_x \sin\theta+P_y \cos\theta \\
= & -\sin\theta\left\{
-g\left(\cos\theta\cfrac{\partial H}{\partial s}
-\sin\theta\cfrac{\partial H}{\partial n}
\right)
\right\}
+\cos\theta\left\{
-g\left(\sin\theta\cfrac{\partial H}{\partial s}
+\cos\theta\cfrac{\partial H}{\partial n}
\right)
\right\} \\
= & g\left(
\cancel{\cos\theta\sin\theta\cfrac{\partial H}{\partial s}}
-\sin^2\theta\cfrac{\partial H}{\partial n}
\cancel{-\cos\theta\sin\theta\cfrac{\partial H}{\partial s}}
-\cos^2\theta\cfrac{\partial H}{\partial s}
\right) \\
=& -g\cfrac{\partial H}{\partial n}\end{split}\]
摩擦項
\(x,y\) 軸方向の摩擦項目はマニング則を用いた場合, (330) より, 以下のように表されます.
(424)\[ \begin{align}\begin{aligned}F_x = & -\cfrac{\tau_x}{\rho h}
= -{{g n_m^2 u \sqrt{u^2+v^2}}\over h^{4/3}} =-u V_\tau\\F_y = & -\cfrac{\tau_y}{\rho h}
= -{{g n_m^2 u \sqrt{u^2+v^2}}\over h^{4/3}} =-v V_\tau\end{aligned}\end{align} \]
ただし,
(425)\[V_\tau = \cfrac{g n_m^2 \sqrt{u^2+v^2}}{h^{4/3}}
= \cfrac{g n_m^2 \sqrt{u_s^2+u_n^2}}{h^{4/3}}\]
(424) 式を, \(s,n\) 軸方向に変換します.
\(F_s, F_n\) を \(s, n\) 方向の摩擦項とします.
(426)\[ \begin{align}\begin{aligned}F_s & = F_x\cos\theta+F_y\sin\theta = -u V_\tau\cos\theta-v V_\tau\sin\theta\\& = -(u_s \cos \theta - u_n \sin \theta)V_\tau\cos\theta
-(u_s \sin \theta + u_n \cos \theta) V_\tau\sin\theta\\& = -u_s V_\tau \cos^2 \theta \cancel{- u_n V_\tau \sin\theta\cos\theta}
-u_s V_\tau \sin^2\theta +\cancel{u_n V_\tau \sin\theta\cos\theta}\\& = -u_s(\sin^2\theta+\cos^2 \theta)V_\tau = -u_s V_\tau
=-{{g n_m^2 u_s \sqrt{u_s^2+u_n^2}}\over h^{4/3}}\end{aligned}\end{align} \]
(427)\[ \begin{align}\begin{aligned}F_n & = -F_x\sin\theta+F_y\cos\theta =u V_\tau\sin\theta-v V_\tau\cos\theta\\& = (u_s \cos\theta - u_n \sin \theta)V_\tau\sin\theta
-(u_s \sin \theta + u_n \cos \theta)V_\tau\cos\theta\\& = \cancel{u_s V_\tau\cos\theta\sin\theta}-u_nV_\tau\sin^2\theta
-\cancel{u_s V_\tau\sin\theta\cos\theta}-u_nV_\tau\cos^2\theta\\& = -u_n(\sin^2\theta+\cos^2 \theta)V_\tau = -u_n V_\tau
=-{{g n_m^2 u_n \sqrt{u_s^2+u_n^2}}\over h^{4/3}}\end{aligned}\end{align} \]
拡散項
\(s-n\) 座標における濃度拡散方程式( (437) 式)と同様の考え方で運動量の拡散については
以下のように表されます.
(428)\[ \begin{align}\begin{aligned}D_s & =
\cfrac{\partial}{\partial s}\left(\nu_t\cfrac{\partial u_s}{\partial s}\right)
+\cfrac{\partial}{\partial n}\left(\nu_t\cfrac{\partial u_s}{\partial n}\right)
+\cfrac{\nu_t}{r}\cfrac{\partial u_s}{\partial n}\\D_n & =\cfrac{\partial}{\partial s}\left(\nu_t \cfrac{\partial u_n}{\partial s}\right)
+\cfrac{\partial}{\partial n}\left(\nu_t\cfrac{\partial u_n}{\partial n}\right)
+\cfrac{\nu_t}{r}\cfrac{\partial u_n}{\partial n}\end{aligned}\end{align} \]
まとめ
以上より, \(s-n\) 座標における2次元自由水面流れの連続式および運動方程式は以下となります.
(429)\[\cfrac{\partial h}{\partial t}
+\cfrac{\partial(hu_s)}{\partial s}
+\cfrac{1}{r}\cfrac{\partial(rhu_n)}{\partial n} =0\]
(430)\[ \begin{align}\begin{aligned}{{\partial u_s}\over{\partial t}}
+u_s{{\partial u_s}\over{\partial s}}
+u_n{{\partial u_s}\over{\partial n}}
-{{u_s u_n}\over{r}}= \hspace{4.5cm}\\-g\cfrac{\partial H}{\partial s}
-{{g n_m^2 u_s \sqrt{u_s^2+u_n^2}}\over h^{4/3}}
+\cfrac{\partial}{\partial s}\left(\nu_t\cfrac{\partial u_s}{\partial s}\right)
+\cfrac{\partial}{\partial n}\left(\nu_t\cfrac{\partial u_s}{\partial n}\right)
+\cfrac{\nu_t}{r}\cfrac{\partial u_s}{\partial n}\end{aligned}\end{align} \]
(431)\[ \begin{align}\begin{aligned}{{\partial u_n}\over{\partial t}}
+u_s{{\partial u_n}\over{\partial s}}
+u_n{{\partial u_n}\over{\partial n}}
+{{u_s^2}\over{r}}= \hspace{4.5cm}\\-g\cfrac{\partial H}{\partial n}
-{{g n_m^2 u_n \sqrt{u_s^2+u_n^2}}\over h^{4/3}}
+\cfrac{\partial}{\partial s}\left(\nu_t \cfrac{\partial u_n}{\partial s}\right)
+\cfrac{\partial}{\partial n}\left(\nu_t\cfrac{\partial u_n}{\partial n}\right)
+\cfrac{\nu_t}{r}\cfrac{\partial u_n}{\partial n}\end{aligned}\end{align} \]
