1次元不等流計算
1次元不等流計算は定常流れ場における開水路の1次元解析法であり,河川の
水面形を計算する基本的な手法であり,現在でも多くの河川の計画高水位の
算定などに使われている手法です.
本テキストで扱う2次元計算では,繰り返し計算における初期水面形の算定法
の一つとして用いられます.
任意断面形における1次元流れの式(不等流の式)は次式で表されます.
(448)\[\cfrac{dH}{dx}+\cfrac{d}{dx}\left(\alpha_e\cfrac{V^2}{2g}\right)+I_e=0\]
ただし, \(H\) は水位, \(x\) は流下方向距離, \(V\) は断面平均流速
\(g\) は重力加速度, \(I_e\) はエネルギー勾配, \(\alpha_e\) はエネルギー補正係数
です. 詳細は [Ref:37] で詳しく解説されていますので省略しますが,
\(I_e\) および \(\alpha_e\) は以下ように表されます.
(449)\[I_e = \cfrac{Q^2}{\left(
\sum\limits_{j=1}^{n_y} \cfrac{1}{n_{mj}} h_j^{5/3} \Delta y_j
\right)^2}\]
(450)\[ \begin{align}\begin{aligned}\alpha_e & =\cfrac{\sum\limits_{j=1}^{n_y} u_j^3 \Delta y_j}
{V^3 A}
=\cfrac{\sum\limits_{j=1}^{n_y} u_j^3 \Delta y_j}
{Q^3/A^2}\\ & =\cfrac{\sum\limits_{j=1}^{n_y}
\left(\cfrac{1}{n_{mj}}h_j^{2/3}I_{ej}^{1/2}\right)^3 h_j \Delta y_j}
{\left(
\sum\limits_{j=1}^{n_y} \cfrac{1}{n_{mj}} h^{5/3}_j \Delta y_j I_e^{1/2}
\right)^3/A^2}
=\cfrac{A^2 \sum\limits_{j=1}^{n_y}
\left(\cfrac{1}{n_{mj}} h_j^3 \Delta y_j \right)}
{\left(
\sum\limits_{j=1}^{n_y} \cfrac{1}{n_{mj}} h^{5/3}_j \Delta y_j \right)^3}\end{aligned}\end{align} \]
(451)\[\alpha_e\cfrac{V^2}{2g} =
\cfrac{A^2 \sum\limits_{j=1}^{n_y}
\left(\cfrac{1}{n_{mj}} h_j^3 \Delta y_j \right)}
{\left(
\sum\limits_{j=1}^{n_y} \cfrac{1}{n_{mj}} h^{5/3}_j \Delta y_j \right)^3}
\cfrac{V^2}{2g}
= \cfrac{Q^2}{2g}
\cfrac{\sum\limits_{j=1}^{n_y}
\left(\cfrac{1}{n_{mj}} h_j^3 \Delta y_j \right)}
{\left(
\sum\limits_{j=1}^{n_y} \cfrac{1}{n_{mj}} h^{5/3}_j \Delta y_j \right)^3}\]
ただし, \(n_y\) は横断方向分割数, \(n_{mj}\) , \(h_j\) および \(u_j\) は
断面を横断方向に分割した時の \(j\) 番目のマニングの粗度係数, 水深
および流速です.分割方法は Figure 155 のようになります.
また, \(Q\) は流量, \(A\) は断面積, \(V\) は断面平均流速です.
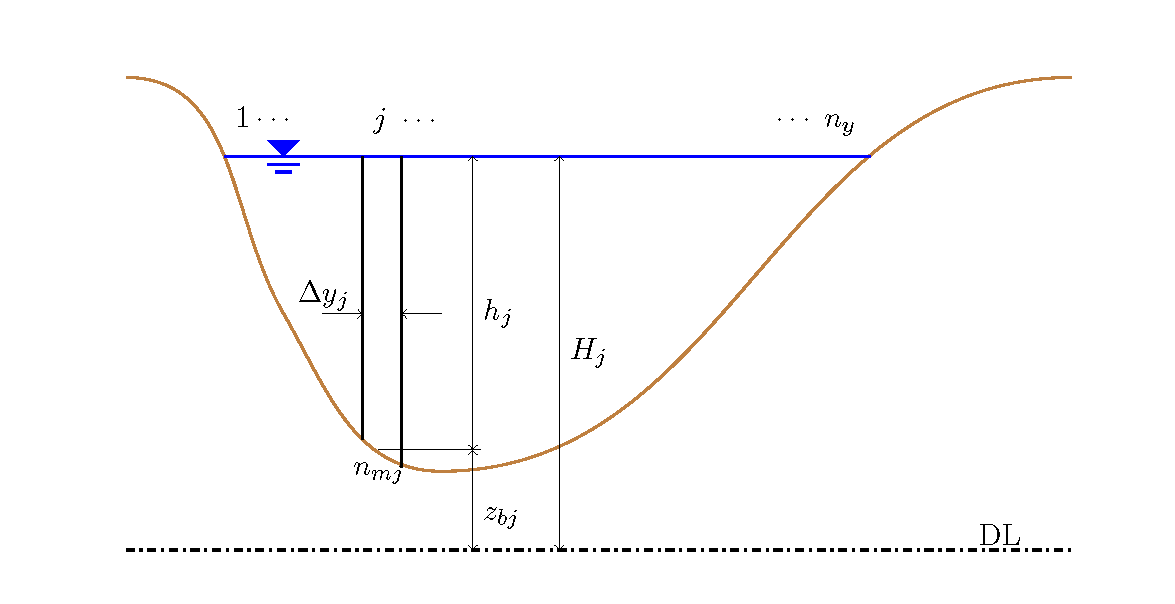
Figure 155 : 断面の横断方向分割
流路の上流から下流に向かって \(i-1\) 番目の断面と \(i\) 番目の断面間距離を
\(\Delta x\) として (448) を差分表示します.
(452)\[ \begin{align}\begin{aligned}\cfrac{H_{i}-H_{i-1}}{\Delta x} \hspace{10cm}\\+
\cfrac{1}{2g}\cfrac{Q^2}{\Delta x}\left[
\left\{
\cfrac{\sum\limits_{j=1}^{n_y}
\left(\cfrac{1}{n_{mj}} h_j^3 \Delta y_j \right)}
{\left(
\sum\limits_{j=1}^{n_y} \cfrac{1}{n_{mj}} h^{5/3}_j \Delta y_j \right)^3}
\right\}_i
-\left\{
\cfrac{\sum\limits_{j=1}^{n_y}
\left(\cfrac{1}{n_{mj}} h_j^3 \Delta y_j \right)}
{\left(
\sum\limits_{j=1}^{n_y} \cfrac{1}{n_{mj}} h^{5/3}_j \Delta y_j \right)^3}
\right\}_{i-1}\\\right]\\+\cfrac{Q^2}{2} \left[
\left\{
\cfrac{1}{\left(
\sum\limits_{j=1}^{n_y} \cfrac{1}{n_{mj}} h_j^{5/3} \Delta y_j
\right)^2} \right\}_{i} +
\left\{
\cfrac{1}{\left(
\sum\limits_{j=1}^{n_y} \cfrac{1}{n_{mj}} h_j^{5/3} \Delta y_j
\right)^2} \right\}_{i-1}
\right]\end{aligned}\end{align} \]
上式において \(i\) が下流側, \(i-1\) が上流側ですので,常流の場合は下流端の水位
を境界条件として与え,\(H_i \rightarrow H_{i-1}\) に向かって順次計算することによって
水位は求まって行きます.
2次元蛇行河川の計算[ 蛇行河川流れの計算(実践編) ]の計算コード [ ref:sn_Nays2D_code ]の中で
初期水位分布の設定法の一つとして,この不等流計算法が用いられています.
