s-n座標における拡散方程式の誘導
\(s-n\) 座標を直交曲線座標とします. \(s-n\) 座標において, \(s\) 軸は任意の曲線, \(n\) 軸は s 軸に直交する直線座標軸とします.
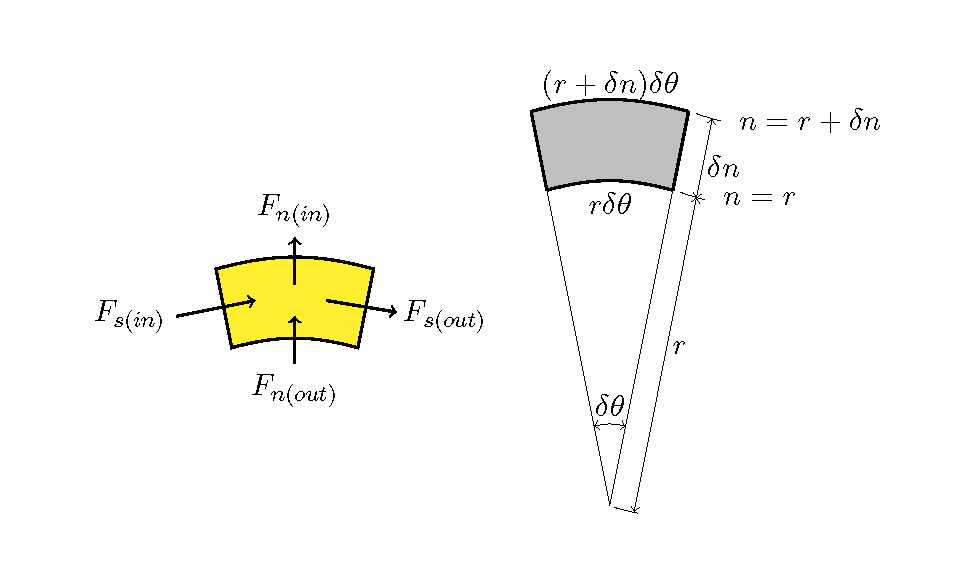
Figure 153 : \(s-n\) 座標の微小要素における濃度Flux収支
拡散する物質の濃度を \(c\) とし,拡散による \(s, n\) 方向の単位幅Fluxおよび拡散係数をそれぞれ,
\(F_s, F_n\) , および \(D_s, D_n\) とすると,以下の関係で表されます.
(432)\[F_s=-D_s\cfrac{\partial F_s}{\partial s}, \hspace{2cm}
F_n=-D_n\cfrac{\partial F_n}{\partial n}\]
Figure 153 に示す微小要素における微小時間の濃度収支を考えると, 微小要素の面積が \(r\, \delta\theta\, \delta n\)
であることを考慮して次式が得られます.
(433)\[\cfrac{\partial c}{\partial t} r\, \delta\theta\, \delta n
=F_{n(n)}r \delta\theta - F_{n(n+\delta n)} (r+\delta n) \delta\theta
+F_{s(s)}\delta n -F_{s(s+\delta s)}\delta n\]
(434)\[\cfrac{\partial c}{\partial t}=\cfrac{F_{n(n)}}{\delta n}-\cfrac{F_{n(n+\delta n)}\, (r+\delta n)}{r\delta n}
+\cfrac{F_{s(s)}-F_{s(s+\delta s)}}{\delta s}\]
ここで,
(435)\[\cfrac{(r+\delta n)}{r\delta n}=\cfrac{1}{r}+\cfrac{1}{\delta n}\]
なので,(434) 式の右辺第2項は,
(436)\[\cfrac{F_{n(n+\delta n)}\, (r+\delta n)}{r\delta n}=
\cfrac{F_{n(n+\delta n)}}{r}+\cfrac{F_{n(r+\delta n)}}{\delta n}\]
となり, 結局 (434) 式は以下のようになります.
(437)\[ \begin{align}\begin{aligned}\cfrac{\partial c}{\partial t} & =\cfrac{F_{n(n)}}{\delta n}-\cfrac{F_{n(n+\delta n)}}{\delta n}
-\cfrac{F_{n(n+\delta n)}}{r}+\cfrac{F_{s(s)}-F_{s(s+\delta s)}}{\delta s}\\& =-\cfrac{\partial F_n}{\partial n}-\cfrac{1}{r}F_{n(r+\delta n)}-\cfrac{\partial F_s}{\partial s}\\& =\cfrac{\partial}{\partial s}\left(D_s \cfrac{\partial c}{\partial s}\right)
+\cfrac{\partial}{\partial n}\left(D_n\cfrac{\partial c}{\partial n}\right)
+\cfrac{D_n}{r}\cfrac{\partial c}{\partial n}\end{aligned}\end{align} \]
\(D_s=D_n=D\) の場合は,
(438)\[\cfrac{\partial c}{\partial t}=D \left(
\cfrac{\partial^2 c}{\partial s^2}+\cfrac{\partial^2 c}{\partial n^2}+
\cfrac{1}{r}\cfrac{\partial c}{\partial n}
\right)\]
となります.
s-n座標における連続式の誘導(別解)
\(s-n\) 座標を直交曲線座標とします. \(s-n\) 座標において, \(s\) 軸は任意の曲線, \(n\) 軸は s 軸に直交する直線座標軸とします.
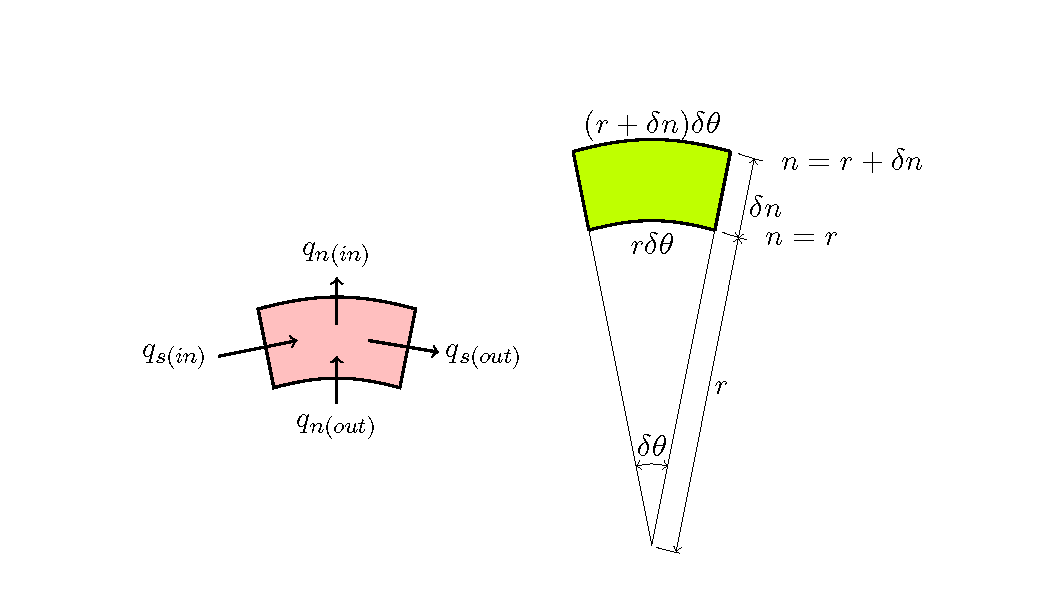
Figure 154 : \(s-n\) 座標の微小要素におけるFlux収支
ただし, \(q_s, q_n\) は流量Fluxです. Figure 154 に示す微小要素における微小時間の流量Flux収支を考えると, 微小要素の面積が \(r\, \delta\theta\, \delta n\)
であることを考慮して次式が得られます.
(439)\[\cfrac{\partial h}{\partial t} r\, \delta\theta\, \delta n
=q_{n(n)}r \delta\theta - q_{n(n+\delta n)} (r+\delta n) \delta\theta
+q_{s(s)}\delta n -q_{s(s+\delta s)}\delta n\]
(440)\[\cfrac{\partial h}{\partial t}=\cfrac{q_{n(n)}}{\delta n}-\cfrac{q_{n(n+\delta n)}\, (r+\delta n)}{r\delta n}
+\cfrac{q_{s(s)}-q_{s(s+\delta s)}}{\delta s}\]
ただし \(h\) は微小要素内の平均水深です. ここで,
(441)\[\cfrac{(r+\delta n)}{r\delta n}=\cfrac{1}{r}+\cfrac{1}{\delta n}\]
なので,(440) 式の右辺第2項は,
(442)\[\cfrac{q_{n(n+\delta n)}\, (r+\delta n)}{r\delta n}=
\cfrac{q_{n(n+\delta n)}}{r}+\cfrac{q_{n(r+\delta n)}}{\delta n}\]
となり, 結局 (440) 式は以下のようになります.
(443)\[ \begin{align}\begin{aligned}\cfrac{\partial h}{\partial t} & =\cfrac{q_{n(n)}}{\delta n}-\cfrac{q_{n(n+\delta n)}}{\delta n}
-\cfrac{q_{n(n+\delta n)}}{r}+\cfrac{q_{s(s)}-q_{s(s+\delta s)}}{\delta s}\\& =-\cfrac{\partial q_n}{\partial n}-\cfrac{1}{r}q_{n(r+\delta n)}-\cfrac{\partial q_s}{\partial s}\end{aligned}\end{align} \]
ここで,
(444)\[\cfrac{\partial(rq_n)}{\partial n}=r\cfrac{\partial q_n}{\partial n}+q_n\cfrac{\partial r}{\partial n}=r\cfrac{\partial q_n}{\partial n}+q_n\]
より,
(445)\[\cfrac{1}{r}\cfrac{\partial(rq_n)}{\partial n}=\cfrac{\partial q_n}{\partial n}+\cfrac{q_n}{r}\]
したがって,
(446)\[\cfrac{\partial h}{\partial t}+\cfrac{\partial q_s}{\partial s}+\cfrac{1}{r}\cfrac{\partial(rq_n)}{\partial n}=0\]
または,
(447)\[\cfrac{\partial h}{\partial t}+\cfrac{\partial(hu_s)}{\partial s}+\cfrac{1}{r}\cfrac{\partial(rhu_n)}{\partial n}=0\]

