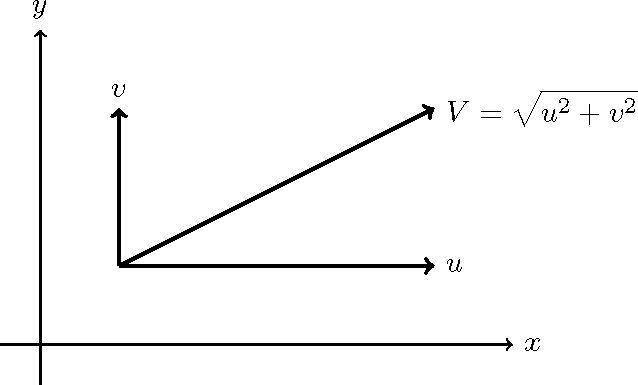移流方程式の理論解
移流方程式,
(318) \[\cfrac{\partial f}{\partial t}+c\cfrac{\partial f}{\partial x}=0\]
において,
(319) \[\begin{split}X=x-ct \\
T= \; \; t\end{split}\]
なる変数変換を行います.これは, \(c\) という速度で移動する原点と一緒に移動する( \(X,T\) )なる
新しい座標を設けることに相当する.これは,例えばもともとの空間に速度 \(c\) で移動
する自動車を走らせ,その自動車の中に原点が自動車と一緒にに移動する \(X\) 軸を持つ
座標を配置するということに相当します.
(319) 式より,
(320) \[\begin{split}\cfrac{\partial}{\partial x}=\cfrac{\partial X}{\partial x} \cfrac{\partial}{\partial X}
+\cfrac{\partial T}{\partial x} \cfrac{\partial}{\partial T}\\
\cfrac{\partial}{\partial t}=\cfrac{\partial X}{\partial t} \cfrac{\partial}{\partial X}
+\cfrac{\partial T}{\partial t} \cfrac{\partial}{\partial T}\end{split}\]
ここで,
(321) \[\cfrac{\partial X}{\partial x}=1, \; \;
\cfrac{\partial X}{\partial t}=0, \; \;
\cfrac{\partial T}{\partial x}=1, \; \;
\cfrac{\partial T}{\partial t}=0\]
なので,
(322) \[\cfrac{\partial}{\partial x} = \cfrac{\partial}{\partial X}, \; \;
\cfrac{\partial}{\partial t} = -c \cfrac{\partial}{\partial X} + \cfrac{\partial}{\partial T}\]
(322) 式を (318) 式に代入すると,
(323) \[\cfrac{\partial f}{\partial t}+c\cfrac{\partial f}{\partial x} =
-u\cfrac{\partial f}{\partial X} +
\cfrac{\partial f}{\partial T} + u\cfrac{\partial f}{\partial X} =
\cfrac{\partial f}{\partial T} =0\]
すなわち, \(c\) という速度で移動する移動する( \(X,T\) )なる
座標においては,
(324) \[\cfrac{\partial f}{\partial T} =0 \; \; \; \mbox{または} \; \; \;
f=\mbox{一定}\]
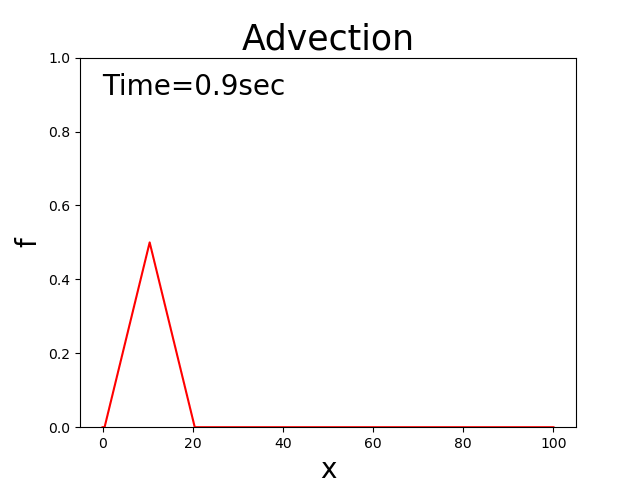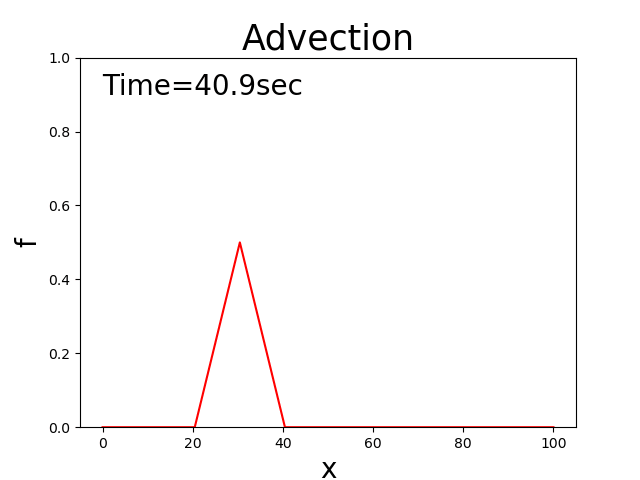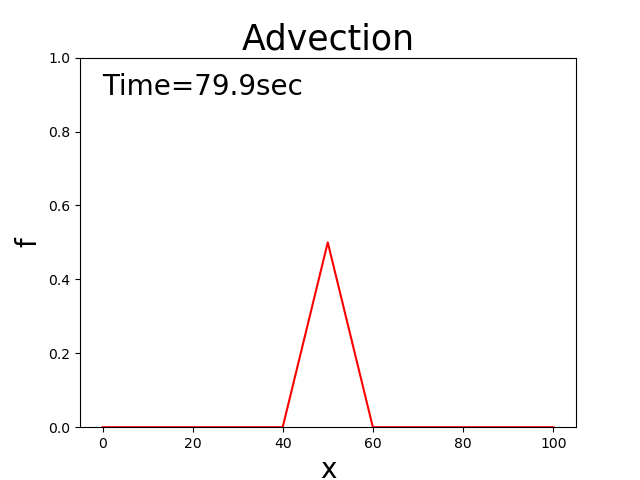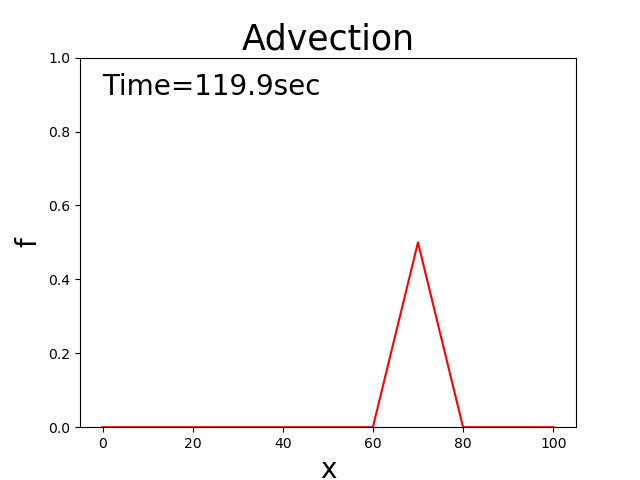
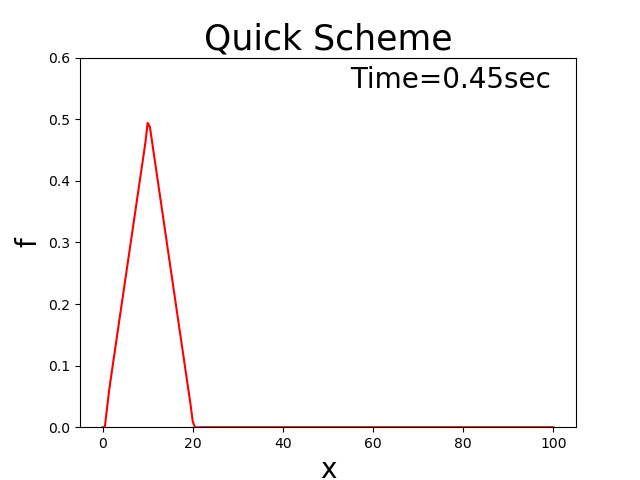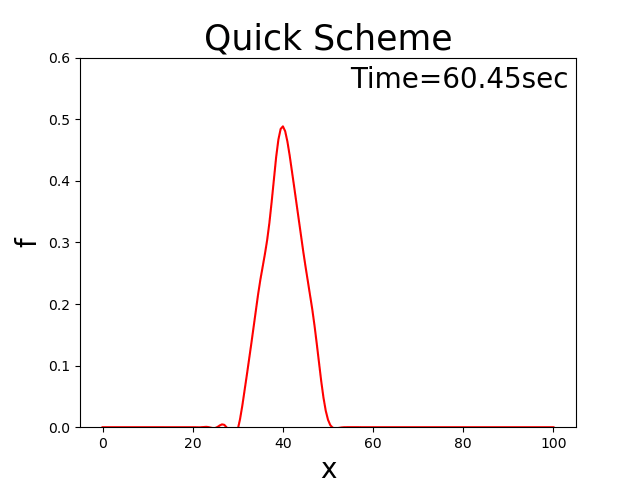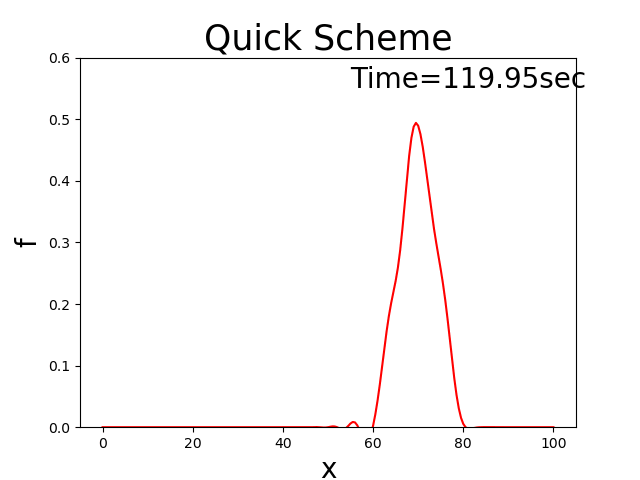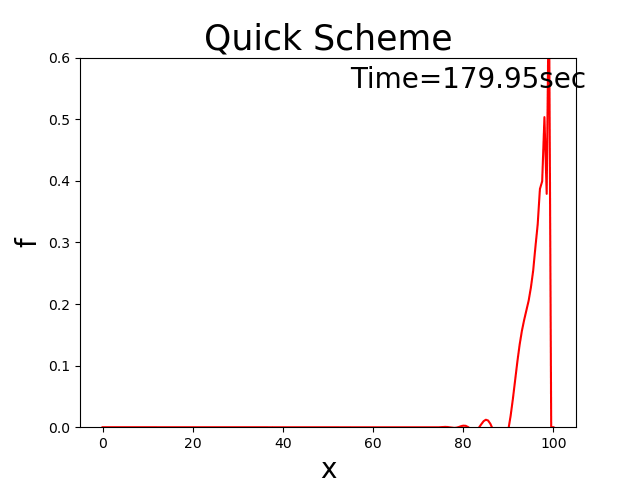
これを言い換えれば, \(c\) という速度で移動しながら \(f\) の分布が一定に保たれる
ということです.
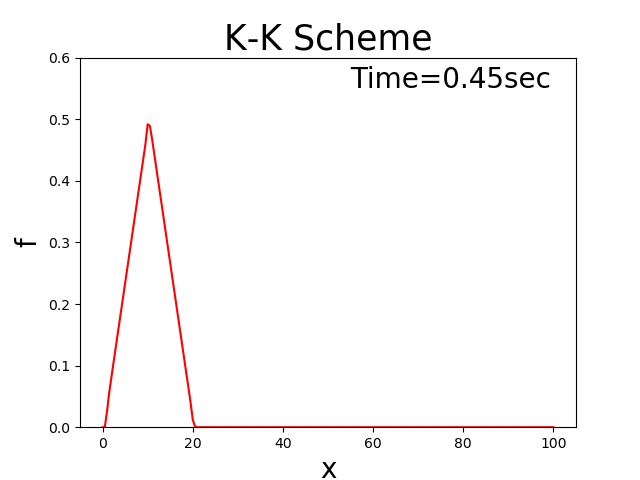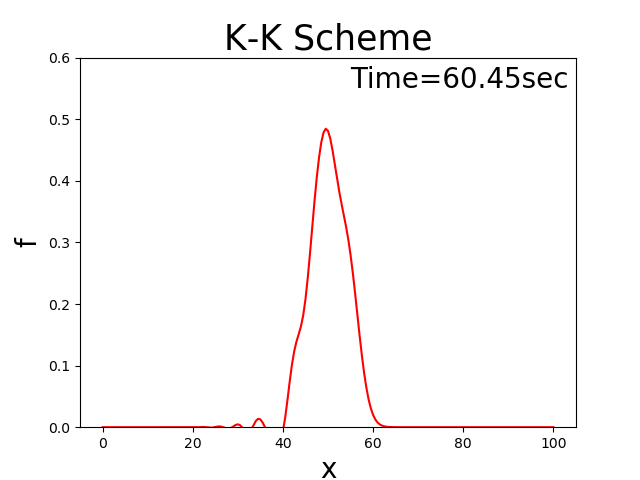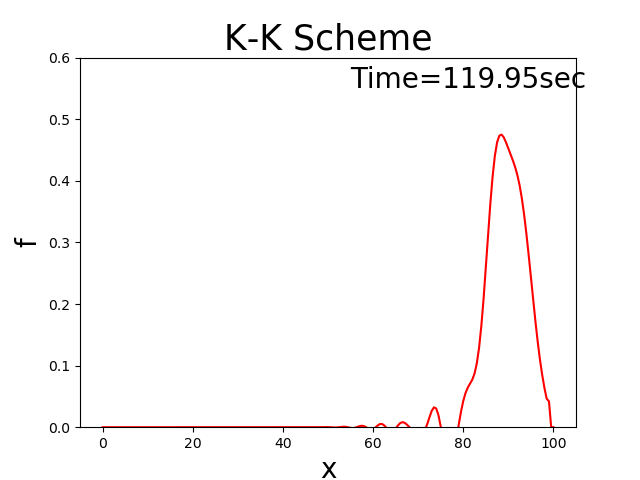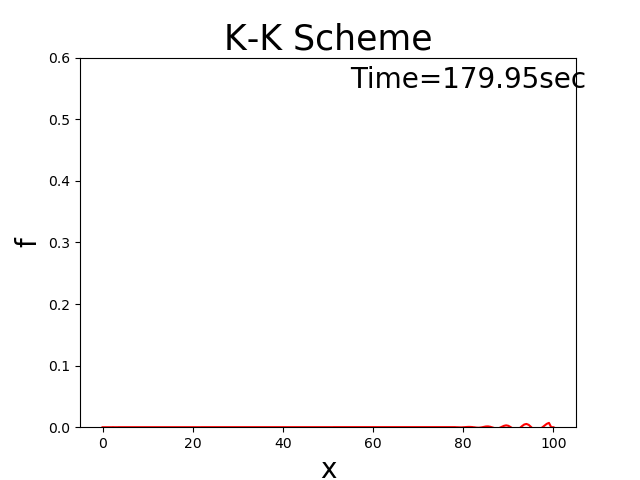
例えば初期分布が三角形分布の場合,Figure 142
Figure 142 : 移流方程式の理論解
河床せん断力の表現方法について
Figure 146 : 流速の成分表示
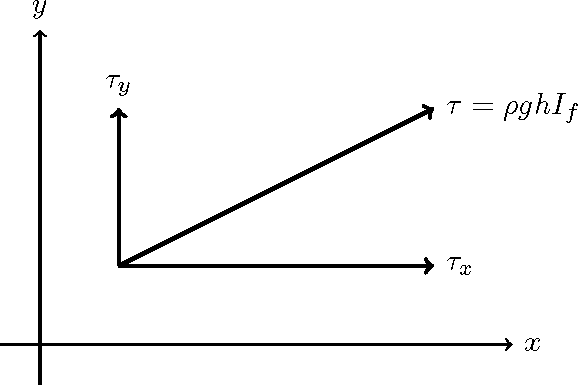
Figure 147 : 河床せん断力の成分表示
Figure 146 Figure 147 \(V=\sqrt{u^2+v^2}\)
をマニングの式で表すと,
(328) \[V={1 \over n_m} h^{2/3} I_e^{1/2}\]
となります. ただし, \(I_e\) はエネルギー勾配です. したがって, 合成流速 \(V\) による河床せん断力
\(\tau\) は,
(329) \[\tau=\rho g h I_e = {{\rho g n_m^2 V^2}\over{h^{1/3}}}\]
となります. (329) 式および Figure 146 Figure 147 \(\tau\) を \(x, y\) 方向に分離して表現すると以下のようになります.
(330) \[\begin{split}\tau_x = \tau { u \over V} = {{\rho g n_m^2 u \sqrt{u^2+v^2}}\over h^{1/3}} \\
\tau_y = \tau { v \over V} = {{\rho g n_m^2 u \sqrt{u^2+v^2}}\over h^{1/3}}\end{split}\]
河岸(側壁)摩擦抵抗について
一般に流下方向に沿った壁面に作用するせん断力は, \(c_w\) を
摩擦係数,\(\tau_w\) を壁面せん断力, \(\rho\) を
流体の密度, \(u_w\) を壁面に沿った流速として,
(331) \[\cfrac{\tau_w}{\rho}=c_w u_w^2\]
で表すことが出来ます.なお,流速の方向(正負)とせん断力の方向を一致させる
ためには,
(332) \[\cfrac{\tau_w}{\rho}=c_w u_w |u_w|\]
となります.
自由水面流れにおける河岸(側壁)のせん断抵抗については \(x\) 方向
の運動方程式 (152) 式の右辺拡散項の \(y\) に関する2回
微分項で考慮する事が可能となります.即ち,
(333) \[\cfrac{\partial}{\partial y}\left( \nu_t \cfrac{\partial u}{\partial y} \right)
=\cfrac{\partial}{\partial y}\left(\cfrac{\tau_w}{\rho}\right)
=\cfrac{1}{\Delta y}\left[
\left( \cfrac{\tau_w}{\rho} \right)_{y+} -
\left( \cfrac{\tau_w}{\rho} \right)_{y-}\right]\]
ただし, 添え字 \(y+\) および \(y-\) は \(y\) 軸の
\(+\) 側と \(-\) 側の値であることを示します.
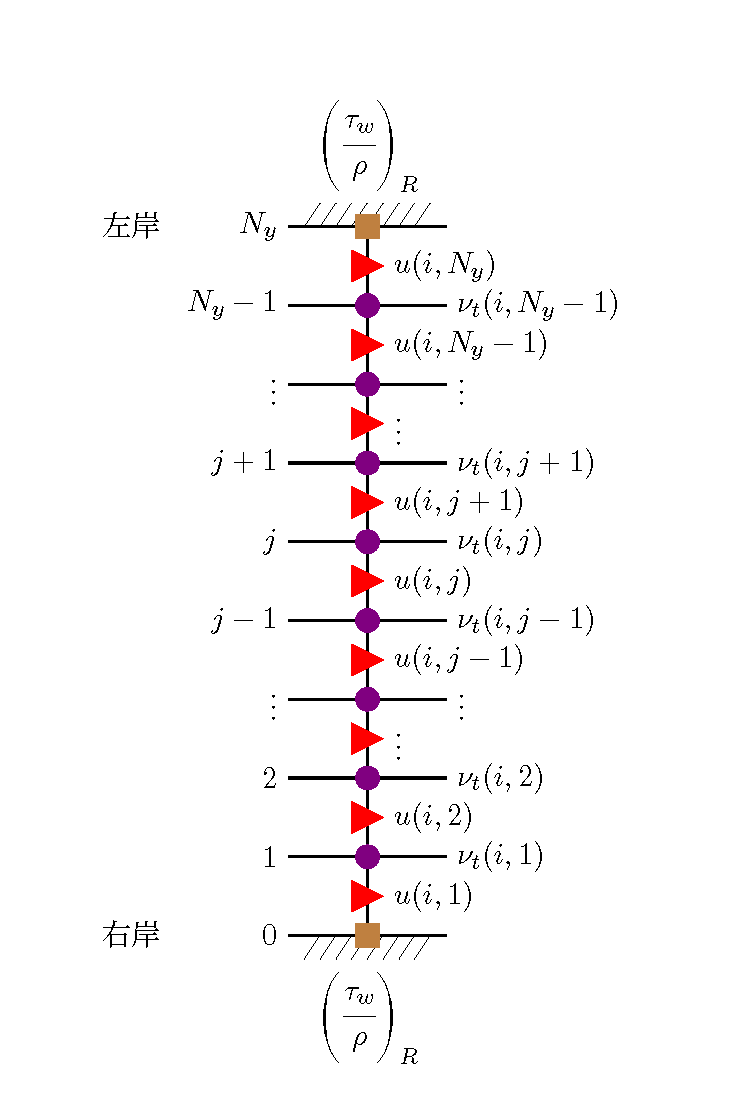
Figure 148 : 横方向せん断力と河岸せん断力の説明図
Figure 148 \(x\) 軸に沿った
せん断力を表すと,河岸以外の河道部分では,
(334) \[\cfrac{\tau_w}{\rho}(i,j)=\cfrac{\nu_t(i,j)}{\Delta y}
\left\{u(i,j+1)-u(i,j)\right\}\]
右岸の河岸においては, (332) 式の関係を用いて.
(335) \[\cfrac{\tau_w}{\rho}(i,0)=c_w u(i,1) |u(i,1)|\]
同様に, 左岸の河岸においては,
(336) \[\cfrac{\tau_w}{\rho}(i,N_y)=c_w u(i,N_y) |u(i,N_y)|\]
となります.
したがって,河岸以外の部分では,
(337) \[\cfrac{\partial}{\partial y}\left( \nu_t \cfrac{\partial u}{\partial y} \right)
=\cfrac{1}{\Delta y}\left[\nu_t(i,j)
\cfrac{u(i,j+1)-u(i,j)}{\Delta y}-\nu_t(i,j-1)\cfrac{u(i,j)-u(i,j-1)}{\Delta y}
\right]\]
右岸河岸では
(338) \[\cfrac{\partial}{\partial y}\left( \nu_t \cfrac{\partial u}{\partial y} \right)
=\cfrac{1}{\Delta y}\left[\nu_t(i,1)
\cfrac{u(i,2)-u(i,1)}{\Delta y}-c_w u(i,1)|u(i,1)|\right]\]
左岸河岸では
(339) \[\cfrac{\partial}{\partial y}\left( \nu_t \cfrac{\partial u}{\partial y} \right)
=\cfrac{1}{\Delta y}\left[c_w u(i,N_y)|u(i,N_y)|
-\nu_t(i,N_y-1)\cfrac{u(i,N_y)-u(i,N_y-1)}{\Delta y}\right]\]
壁面摩擦係数について
底面からある程度離れた側壁近傍においては相対的に底面摩擦の影響が無視可能で,
摩擦の影響は側面からのみ受けると仮定すると,流下方向流速の水平
分布は水平方向に対数則などの理論的な流速分布に従うと考えることが可能です.
後述の鉛直方向の対数則分布式, (359) 式を水平方向に適用すると次式が得られます.
(340) \[\cfrac{u}{u_{\ast w}}=\cfrac{1}{\kappa}\log \cfrac{y}{y_0}\]
ただし, \(u_{\ast w}\) は壁面の摩擦速度, \(\kappa\) はカルマン定数,
\(y\) は水平方向距離です.また, \(y_0\) は流速がゼロとなる点の壁からの距離
で, 壁面が粗面の場合, 後述の (382) 式を適用すると,
(341) \[y_0=\cfrac{k_s}{30}\]
となります.また, \(u_{\ast w}\) は (332) 式の壁面せん断力で表すと,
(342) \[u_{\ast w}|u_{\ast w}|=\cfrac{\tau_w}{\rho}=c_w u_w |u_w|\]
となりますので, \(u_{\ast w} >0\) の場合を考えると,
(343) \[{u_{\ast w}}^2 = c_2 {u_w}^2 \hspace{5mm} \mbox{または}
\hspace{5mm} u_{\ast w}=\sqrt{c_w} u_w\]
となり, \(u_w\) を側壁に最も近い計算点の流速とし,その点の側壁からの距離を
\(y_1\) とすると,
(344) \[\cfrac{u_w}{u_{\ast w}}= \cfrac{1}{\kappa}\ln \cfrac{y_1}{y_0} =
\cfrac{1}{\sqrt{c_w}}\]
となります.これより,
(345) \[c_w= \cfrac{1}{\left(
\cfrac{1}{\kappa}\ln \cfrac{y_1}{y_0}\right)^2}=
\cfrac{\kappa^2}{\left(
\ln \cfrac{30y_1}{k_s}\right)^2}\]
となり,\(c_w\) は側壁の相当粗度高 \(k_s\) と側壁に最も近い流速の計算点の
側壁からの水平距離 \(y_1\) が与えられると, (344) 式から物理定数
として与える事が可能となります.
流速分布について
ここでは水平方向流速の鉛直分布について解説します.
対数流速分布(対数則)
鉛直方向分布式
1次元定常等流の流下方向運動方程式は次式で与えられます.
(346) \[0=-g\cfrac{\partial H}{\partial x}+\cfrac{\partial}{\partial z}
\left(\nu_t \cfrac{\partial u}{\partial z}\right)\]
ここで, \(u\) は流下方向流速, \(g\) は重力加速度, \(H\) は水位, \(x\) は流下方向座標軸,
\(z\) は鉛直方向座標軸, \(\nu_t\) は渦動粘性係数です.
等流なので \(-\cfrac{\partial H}{\partial x}=I_e\) ( \(I_e\) はエネルギー勾配)
であり, また, 河床の高さを \(z_b\) , 水深を \(h`とすると水位は :math:`H (=z_b+h)\) として無次元鉛直座標を,
(347) \[\zeta=\cfrac{z-z_b}{h}\]
で定義すると, (347) 式より, \(\partial z = h \partial \zeta\)
なので,(346) 式は
(348) \[0={u_\ast}^2+ \cfrac{\partial}{\partial \zeta}
\left(\cfrac{\nu_t}{h} \cfrac{\partial u}{\partial \zeta}\right)\]
となります.ただし, \(u_\ast (=\sqrt{g h I_e})\) は摩擦速度です.
(348) 式を \(\zeta\) で積分します.
(349) \[{u_\ast}^2 \zeta + \left(\cfrac{\nu_t}{h} \cfrac{\partial u}{\partial \zeta}\right) + C_1 = 0\]
ただし, \(C_1\) は積分定数です. 水面でせん断力はゼロなので,
\(\zeta=1\) で \(\nu_t \cfrac{\partial u}{\partial \zeta}=0\) ,
より,
(350) \[C_1 = -{u_\ast}^2\]
したがって, (349) 式は,
(351) \[-{u_\ast}^2 (1-\zeta) +\cfrac{\nu_t}{h} \cfrac{\partial u}{\partial \zeta} =0\]
となります.
渦動粘性係数に,以下の放物線分布を用いることにし,
(352) \[\nu_t = \kappa u_\ast h \zeta (1-\zeta)\]
ここで, \(\kappa\) はカルマン定数です. (352) 式を (351) 式に代入すると,
(353) \[-u_\ast\cancel{^2} \cancel{(1-\zeta)} +\cfrac{
\kappa \cancel{u_\ast} \cancel{h} \zeta \cancel{(1-\zeta)}
}{\cancel{h}} \cfrac{\partial u}{\partial \zeta} =0\]
より,
(354) \[-u_\ast + \kappa \zeta \cfrac{\partial u}{\partial \zeta}=0\]
または,
(355) \[\cfrac{\partial u}{\partial \zeta}= \cfrac{u_\ast}{\kappa} \cfrac{1}{\zeta}\]
となります.これを再度 \(\zeta\) で積分して
(356) \[u = \cfrac{u_\ast}{\kappa} \ln \zeta + C_2\]
ただし, \(C_2\) は積分定数です. \(\zeta=\zeta_0\) で
\(u=0\) としますと,
(357) \[C_2=-\cfrac{u_\ast}{\kappa} \ln \zeta_0\]
より以下の対数流速分布式が得られます.
(358) \[\begin{split}\cfrac{u}{u_\ast}=\cfrac{1}{\kappa} \left( \ln \zeta - \ln \zeta_0 \right) \\
=\cfrac{1}{\kappa}\ln \cfrac{\zeta}{\zeta_0}\end{split}\]
または,
(359) \[\cfrac{u}{u_\ast}=\cfrac{1}{\kappa}\ln \cfrac{z}{z_0}\]
ただし, \(z_0=h\zeta_0\) で流速がゼロになる点の河床からの高さです.
対数則ではこの \(z_0\) の大小により河床抵抗の大小が決まります. \(z_0\) の替わりに,
相当粗度高 \(k_s\) を用いる場合は, \(k_s=30z_0\) となることが知られてますので
[ カルマン-プラントルの壁乱流流速式([Ref:31]) \(z_0=k_s/30\) を (359) 式に代入すると,
(360) \[\cfrac{u}{u_\ast}
=\cfrac{1}{\kappa}\ln \cfrac{30z}{k_s}
=\cfrac{1}{\kappa} \left(\ln \cfrac{z}{k_s}+\ln 30 \right)
=\cfrac{1}{\kappa} \left(\ln \cfrac{z}{k_s}+3.4 \right)\]
\(\kappa=0.4\) とすると以下の式になります.
(361) \[\cfrac{u}{u_\ast}=8.5+2.5\ln \cfrac{z}{k_s}
=8.5+5.75\log \cfrac{z}{k_s}\]
対数則による水深平均流速
(358) 式を0から1まで積分します.
(362) \[\begin{split}\cfrac{<u>}{u_\ast}=\cfrac{1}{\kappa}\int_0^1
\left( \ln \zeta - \ln \zeta_0 \right) d\zeta
=\cfrac{1}{\kappa} \left\{ \left[ \zeta \ln \zeta - \zeta \right]_0^1
-\ln \zeta_0 \left[\zeta \right]_0^1 \right\} \\
= \cfrac{1}{\kappa} \left( \ln 1 -1-\ln \zeta_0 \right)
= \cfrac{1}{\kappa} \left( \ln \cfrac{1}{\zeta_0}-1 \right)\end{split}\]
または,
(363) \[\cfrac{<u>}{u_\ast}=\cfrac{1}{\kappa} \left(\ln \cfrac{h}{z_0}-1 \right)\]
ここで相当粗度高 \(k_s\) を導入します. [ カルマン-プラントルの壁乱流流速式([Ref:31]) \(k_s=30z_0\) なので, \(z_0=\cfrac{k_s}{30}\) を用いて,
(364) \[\cfrac{<u>}{u_\ast}
=\cfrac{1}{\kappa}\left(\ln \cfrac{30h}{k_s}-1 \right)
=\cfrac{1}{\kappa}\left(\ln\cfrac{h}{k_s}+\ln 30 -1 \right)
=\cfrac{1}{\kappa}\left(\ln\cfrac{h}{k_s}+2.4 \right)\]
\(\kappa=0.4\) とすると,
(365) \[\cfrac{<u>}{u_\ast}=6.0+2.5\ln\cfrac{h}{k_s}
=6.0+5.75\log\cfrac{h}{k_s}\]
放物線分布
鉛直方向分布式
渦動粘性係数に (352) の替わりに水深方向一定値を用い, (351) 式に適用します.
(366) \[\nu_t = \cfrac{\kappa}{6}u_\ast h\]
これを (351) 式に適用します.
(367) \[-u_\ast\cancel{^2} (1-\zeta) +\cfrac{\kappa \cancel{u_\ast} \cancel{h}}{6 \cancel{h}} \cfrac{\partial u}{\partial \zeta} =0\]
より,
(368) \[\cfrac{\partial u}{\partial \zeta}=\cfrac{6u_\ast}{\kappa}(1-\zeta)\]
\(\zeta\) で積分して,河床( \(\zeta=0\) )で \(u=u_b\) とすると,
(369) \[u=\cfrac{6 u_\ast}{\kappa} \left( \zeta - \cfrac{1}{2} \zeta^2 \right) +u_b\]
または,
(370) \[\cfrac{u}{u_\ast}=\cfrac{6}{\kappa} \left( \zeta - \cfrac{1}{2} \zeta^2 \right) +\cfrac{u_b}{u_\ast}\]
放物線分布における水深平均流速
水深平均流速は (369) 式を \(\zeta=0 \sim 1\) で積分して,
(371) \[\begin{split}<u>=\cfrac{6 u_\ast}{\kappa} \int_0^1 \left( \zeta - \cfrac{1}{2} \zeta^2 \right)
d\zeta + \int_0^1 u_b d\zeta \\
= \cfrac{6 u_\ast}{\kappa} \left[
\cfrac{1}{2} \zeta^2-\cfrac{1}{6} \zeta^3 \right]_0^1 + u_b
=\cfrac{2u_\ast}{\kappa}+u_b\end{split}\]
または,
(372) \[\cfrac{<u>}{u_\ast}=\cfrac{2}{\kappa}+\cfrac{u_b}{u_\ast}\]
対数則と放物線分布の比較
(372) 式より,
(373) \[\cfrac{u_b}{u_\ast}=\cfrac{<u>}{u_\ast}-\cfrac{2}{\kappa}\]
これを, (370) 式に代入すると, 放物線分布式は,
(374) \[\cfrac{u}{u_\ast}=\cfrac{6}{\kappa} \left( \zeta - \cfrac{1}{2} \zeta^2 \right) +
\cfrac{<u>}{u_\ast}-\cfrac{2}{\kappa}
=\cfrac{1}{\kappa} \left( 6\zeta - 3\zeta^2 -2 \right) +
\cfrac{<u>}{u_\ast}\]
放物線分布を対数則と同じ水深平均流速の条件で比較ために,
(374) 式の右辺の \(\cfrac{<u>}{u_\ast}\) に (364) 式の表現を
代入します.
(375) \[\cfrac{u}{u_\ast}=\cfrac{1}{\kappa} \left( 6\zeta - 3\zeta^2 -2 \right) +
\cfrac{1}{\kappa}\left(\ln\cfrac{h}{k_s}+2.4 \right)
=\cfrac{1}{\kappa} \left( 6\zeta - 3\zeta^2 +0.4
+\ln\cfrac{h}{k_s} \right)\]
\(\kappa=0.4\) とすると,
(376) \[\cfrac{u}{u_\ast}=15.0\zeta-7.5\zeta^2+1.0+2.5\ln\cfrac{h}{k_s}
=15.0\zeta-7.5\zeta^2+1.0+5.75\log\cfrac{h}{k_s}\]
一方, 対数則( (360) )のほうも, \(\zeta\) を用いて表すには, \(z=h\zeta\) なので,
(377) \[\cfrac{u}{u_\ast}
=\cfrac{1}{\kappa}\ln \cfrac{30h\zeta}{k_s}
=\cfrac{1}{\kappa}\left(\ln \cfrac{h}{k_s}+\ln 30 +\ln \zeta \right)
=\cfrac{1}{\kappa}\left(\ln \cfrac{h}{k_s}+3.4+\ln \zeta \right)\]
\(\kappa=0.4\) を用いますと.
(378) \[\cfrac{u}{u_\ast}
=8.5+ 2.5\left(\ln \cfrac{h}{k_s}+\ln \zeta \right)
=8.5+ 5.75\left(\log \cfrac{h}{k_s}+\log \zeta \right)\]
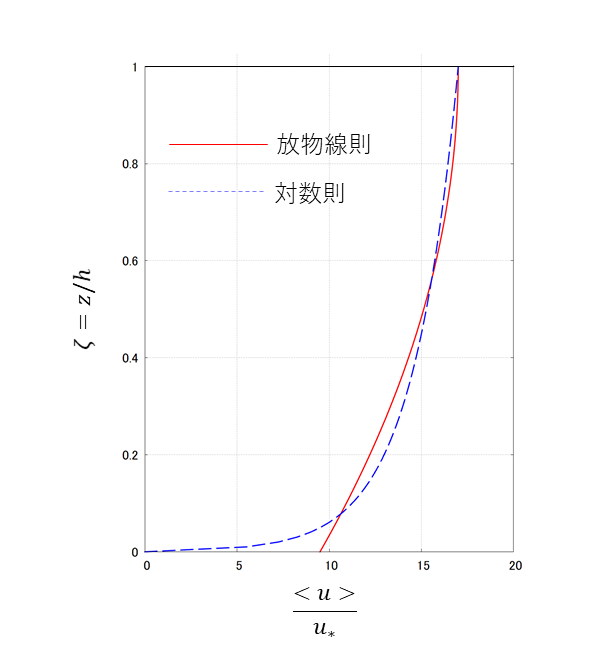
放物線分布式 (375) または (376) 式と, 対数流速分布式(対数則) (377) または
(378) 式を比較したのが Figure 149 Figure 149 \(h/k_s=30\) の場合の例です.
Figure 149 : 対数則と放物線分布の比較
カルマン-プラントルの壁乱流流速式([Ref:31]
カルマン・プラントルは壁乱流の流速式として次式を提案しています( [Ref:31]
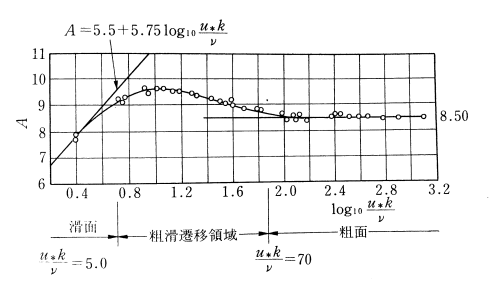
(379) \[\cfrac{u}{u_\ast}= A + \cfrac{1}{\kappa}\ln \cfrac{z}{k_s} =A +5.75\log \cfrac{z}{k_s}\]
ここで, \(u\) は流速, \(\kappa\) はカルマン定数, \(A\) は実験定数, \(u_\ast\) は摩擦速度, \(z\) は壁からの距離, \(k_s\) は粗度高です.
Figure 150 : 流速分布式の定数 \(A\) の算定
Figure 150 \(A=8.5\) の定数が得られ, この結果, (379) 式は,
(380) \[ \cfrac{u}{u_\ast}= 8.5 + \cfrac{1}{\kappa}\ln \cfrac{z}{k_s}\]
となります. これを対数則の理論式, (359) 式と等しいとしますと,
(381) \[\cfrac{u}{u_\ast}=8.5 + \cfrac{1}{\kappa}\ln \cfrac{z}{k_s} = \cfrac{1}{\kappa}\ln \cfrac{z}{z_0}\]
となり, \(\kappa=0.4\) とすると,
(382) \[k_s=29.96 z_0 \approx 30z_0\]
が得られます.
平坦床の粗度について
ここでは,平坦床(河床波の影響が無い状態)での粗度について説明します.
対数則に基づく平均流速式( (365) 式)は指数近似の形のほうが扱いが容易になります.
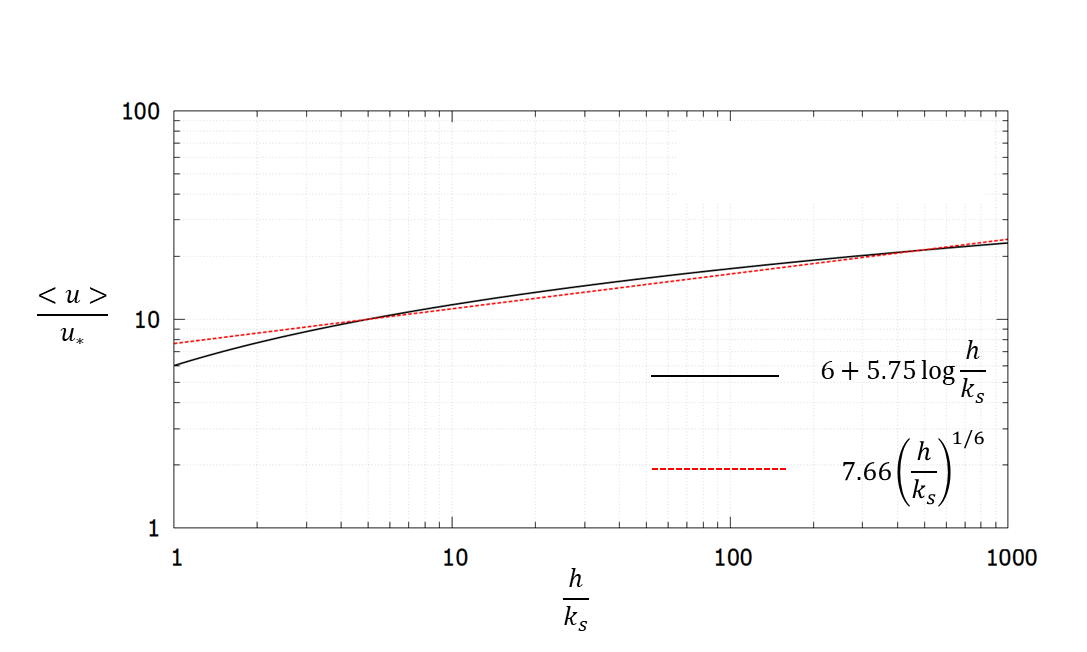
(383) \[\cfrac{<u>}{u_\ast} = 6+5.75 \log{\cfrac{h}{k_s}} \approx
7.66\left(\displaystyle{{h}\over{k_s}}\right)^{1/6}\]
これを図示したのが Figure 151
Figure 151 : 対数流速式の指数近似
マニング粗度係数での表示
マニング則との関係は,\(n_m\) をマニングの粗度係数として
(384) \[<u>=\cfrac{1}{n_m} h^{2/3} I_e^{1/2} = 7.66 \left(\cfrac{h}{k_s}\right)^{\cfrac{1}{6}}
\sqrt{g h I_e}\]
より,
(385) \[n_m = \cfrac{1}{7.66} \cfrac{{k_s}^{1/6}}{g^{1/2}}\]
または,
(386) \[k_s = (7.66 n_m g^{1/6})^6 = 2.02 \times 10^5 g {n_m}^6\]
となります.マニング則では単位として[meter, sec]が用いられるますので,
\(g\) =9.8(m/s \(^2\) )として,
(387) \[n_m=0.0415 {k_s}^{1/6} \mbox{ または } k_s=1.98 \times 10^6 {n_m}^6\]
となり, 河床が平坦な場合,相当粗度高 \(k_s=2d\) ( \(d\) は河床材料の粒径)を用いると,
(388) \[n_m=0.015d^{1/6}\]
が得られます.ただし \(d\) は[mm]単位です.
抵抗係数・流速係数との関係
抵抗係数として用いられる流速係数 \(\varphi\) や摩擦係数 \(C_f\) で
平坦床河床の粗度を河床材料の粒径で表す場合は,以下のような表現になります.
(389) \[\cfrac{<u>}{u_\ast} = \varphi = \cfrac{1}{\sqrt{C_f}}\]
より,
(390) \[\begin{split}C_f = \cfrac{1}{\varphi^2} = \cfrac{{u_\ast}^2}{<u>^2} \\
\varphi = \cfrac{h^{1/6}}{n_m \sqrt{g}} \\
C_f = \cfrac{g {n_m}^2}{h^{1/3}}\end{split}\]
などとなります.