この節の作者: 清水康行 <yasu@i-ric.org>

本テキストへの感想, 質問, 要望, バグ報告などはこちらへお願いします.

移動床河川水理学の基礎知識

注釈

本節の執筆に際しては北見工業大学の渡邊康玄教授および寒地土木研究所の 川村(山口)里実主任研究員に画像・動画の提供や多くのアドバイスを受けました． 以下の解説の多くの部分が両氏の研究成果の引用となっております． ここに記して謝意を表します．

移動床河川とは，土砂移動を伴う河川のことで，一般の河川のほとんどは 移動床河川です．ここでは移動床河川における水理学での最低限の基礎知識について解説します．

河床形態と河道形態

河床形態とは移動床河川における河底の形状のことであり，河道形態とは平面 形状の形態のことです．河床形態や河道形態は河床や河岸の浸食・堆積になどの 河床や河岸の変動に伴い形成される地形のことで，その規模別に小規模・中規模・大規模 に分類されます．なお，河床変動と河岸変動を合わせて河床変動と言われる場合もあります．

小規模とは河床材料の粒径の規模，中規模とは水深や川幅の規模，大規模とは 河川縦断方向の距離の規模のことで， 例えば小規模河床変動とは粒子スケールの河床変動で，小規模河床変動の結果として 現れる河床形態を小規模河床形態と言い，単純に河床波とも呼ばれます．

河床変動および河道・河床形態の規模はそのスケールを基準に概ね下記のように分類されます．

Table 6 河床変動および河床・河道形態の規模

規模	スケール	実例	モデルの次元
大規模 河床変動	川幅の数倍以上 \(10^2 \sim 10^5\) (m)	河道縦断形状 ダム下流の河床変動 ダム堆砂	1次元モデル
中規模 河床形態	川幅・水深スケール \(10^0 \sim 10^3\) (m)	蛇行，固定砂州 交互(単列)砂州，複列・網状砂州 構造物周辺の局所洗堀	平面2次元モデル 3次元モデル
小規模 河床形態	河床砂粒子スケール \(10^{-2} \sim 10^0\) (m)	砂堆(dune), 反砂堆(anti dune) 砂漣(ripple)	鉛直2次元モデル

土木学会水理委員会(現在の水工学委員会)によって示されている河床形態の分類は以下の通りです．[Ref:13]

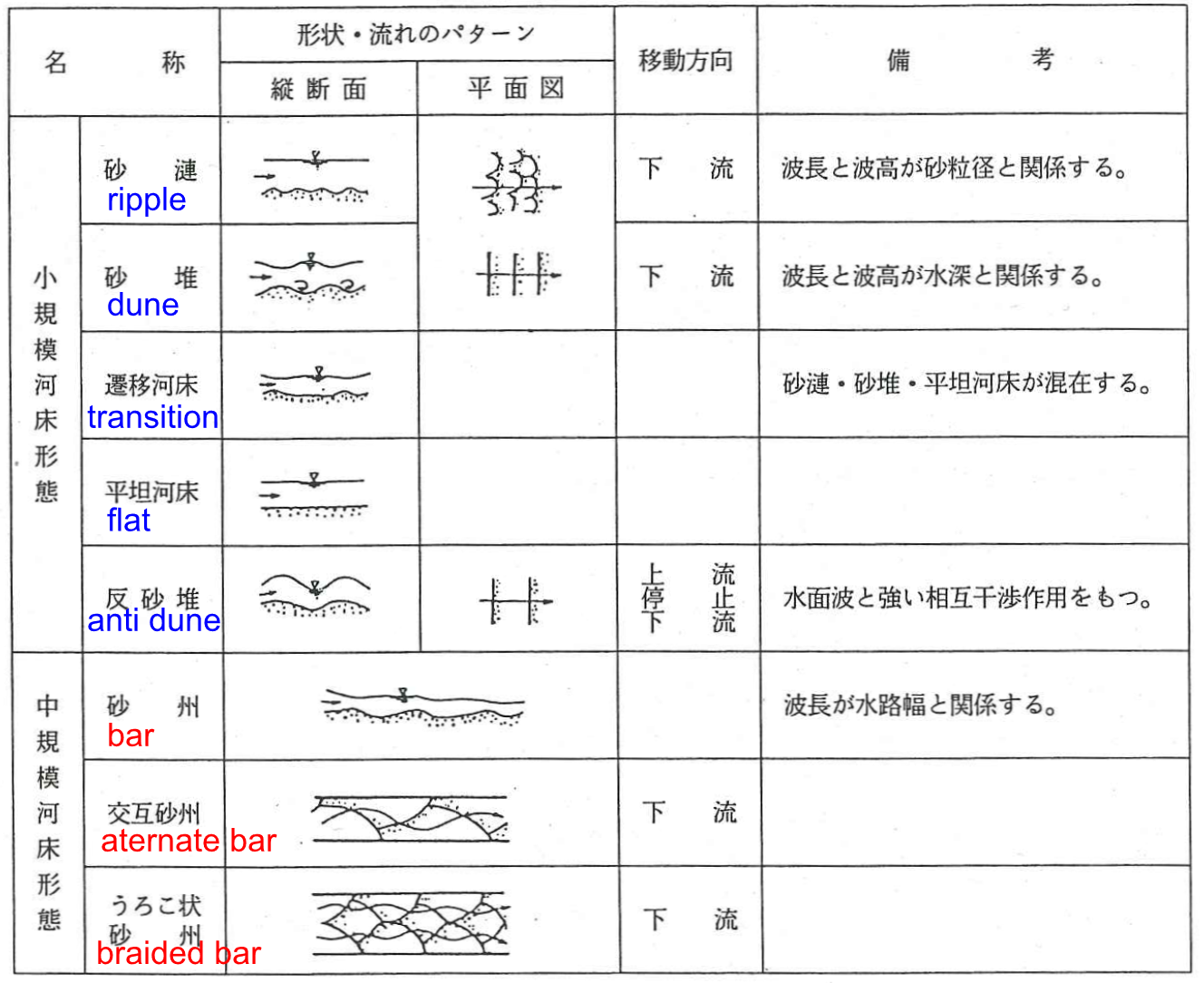
Figure 48 : 河床形態の分類(土木学会)

小規模河床形態の形状特性

Figure 49 は Garcia [Ref:15] による小規模河床形態の発達過程を表したものです． これによれば, フルード数 \(F_r\) の上昇に伴い，小規模河床形態が変化(発達)するのが分かります． なお，フルード数が低い状態の流れ(凡そ \(F_r < 0.8\) )の流れをLower Regime, フルード数が高い状態の流れ( \(Fr>1.0\) )の流れを Upper Regimeと呼ばれます．

イメージとしては，ある水路(河川)で流量を徐々に増やして行くと，最初は流砂が存在しない平坦な状態から， 粒径規模の砂漣→砂漣と砂堆の混在→安定した砂堆→砂堆の不安定化→砂堆の消失と河床の平坦化→定在波の発生→反砂堆 というプロセスになります．なお，小規模河床形態は発達過程と減衰過程では異なった挙動を示すことが知られており， これを，抵抗の二価性とか，ヒステリシス現象などと呼ばれます． なお，河床の抵抗(粗度)は小規模河床形態(河床波)の形状に大きく依存しますので，河川の粗度係数の算定には小規模河床形態に関する検討が極めて重要となります. 詳しくは岸・黒木の研究 [Ref:32] などを参照下さい．なお，本テキストでは平坦河床の場合(河床波の影響が無い場合)の粗度について 平坦床の粗度について で簡単に解説しております．

Figure 49 : 小規模河床形態の分類 (Garcia [Ref:15] )

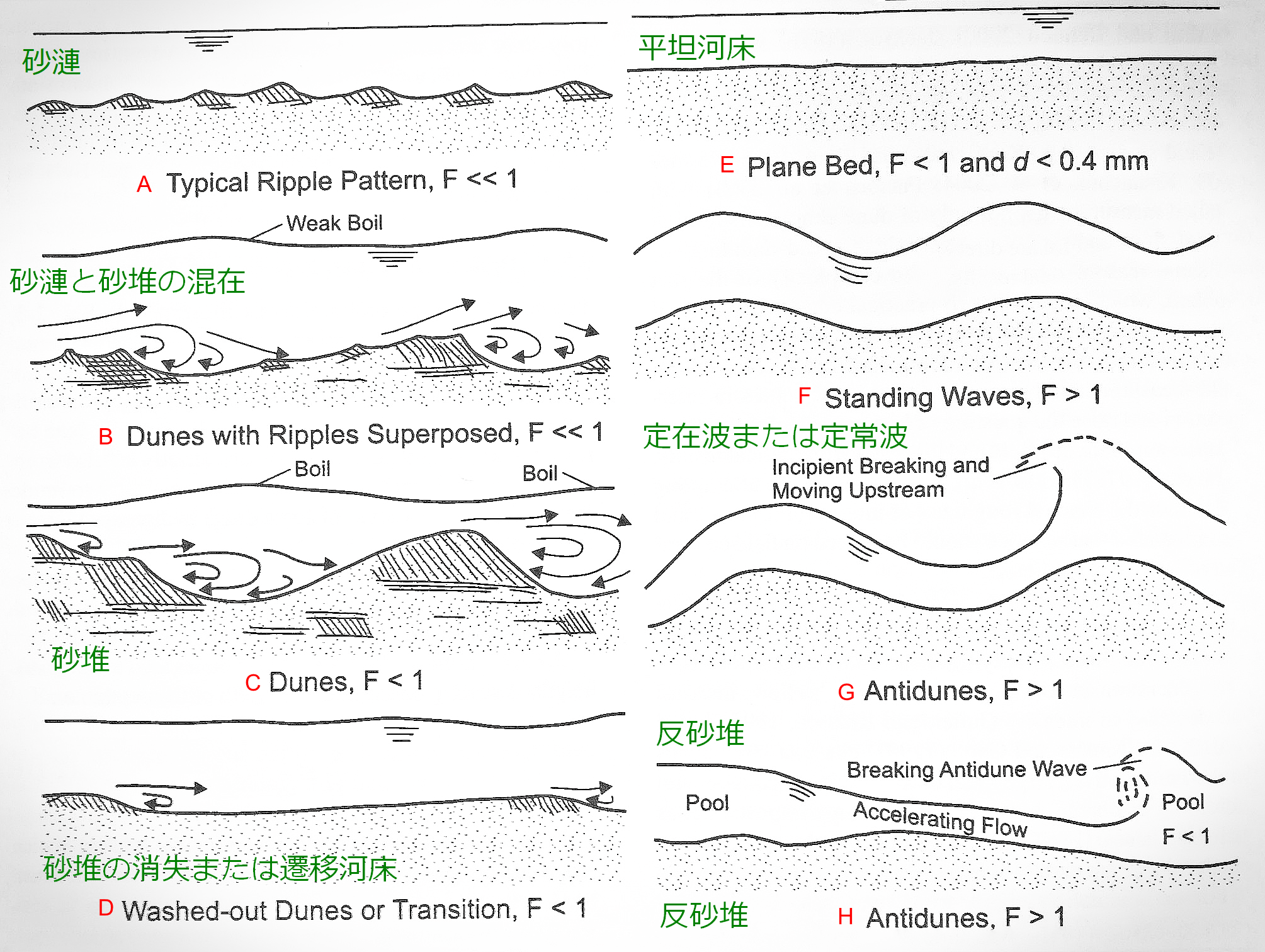
[Ref:13] によれば，一般的に小規模河床形態(河床波)は不安定であって波長や波高の特性を 系統的に整理するのは難しいとしつつも，以下のような概念が紹介されています．

砂堆(dune)の波長と波高

Figure 50 は土木学会水理委員会 [Ref:13] による砂漣・砂堆が発生時の平均水深 \(h\) と 砂漣・砂堆の波長 \(\lambda_s\) ・の比を河床材料の 粒子レイノルズ数 \(u_\ast d_{50}/\nu\) との関係で表したものです. ここで, \(d_{50}\) は50%粒径, \(u_{\ast}\) は摩擦速度【 掃流力と限界掃流力 を参照】, \(\nu\) は水の 動粘性係数です. この結果, \(u_\ast d_{50}/\nu \approx 20\) を境界に \(h/\lambda_s\) の特性は大きく異なることが分かります．すなわち,

• \(u_\ast d_{50}/\nu > 20\) で砂堆(dune)が発生し，このとき \(h/\lambda_s\) ははぼ一定となり平均的には \(\lambda_s \approx 5h\) となる．

• \(u_\ast d_{50}/\nu < 20\) で砂漣(ripple)が発生し, このとき \(h/\lambda_s\) は大きく変化し両者の間に有意な関係は無くなるなる．

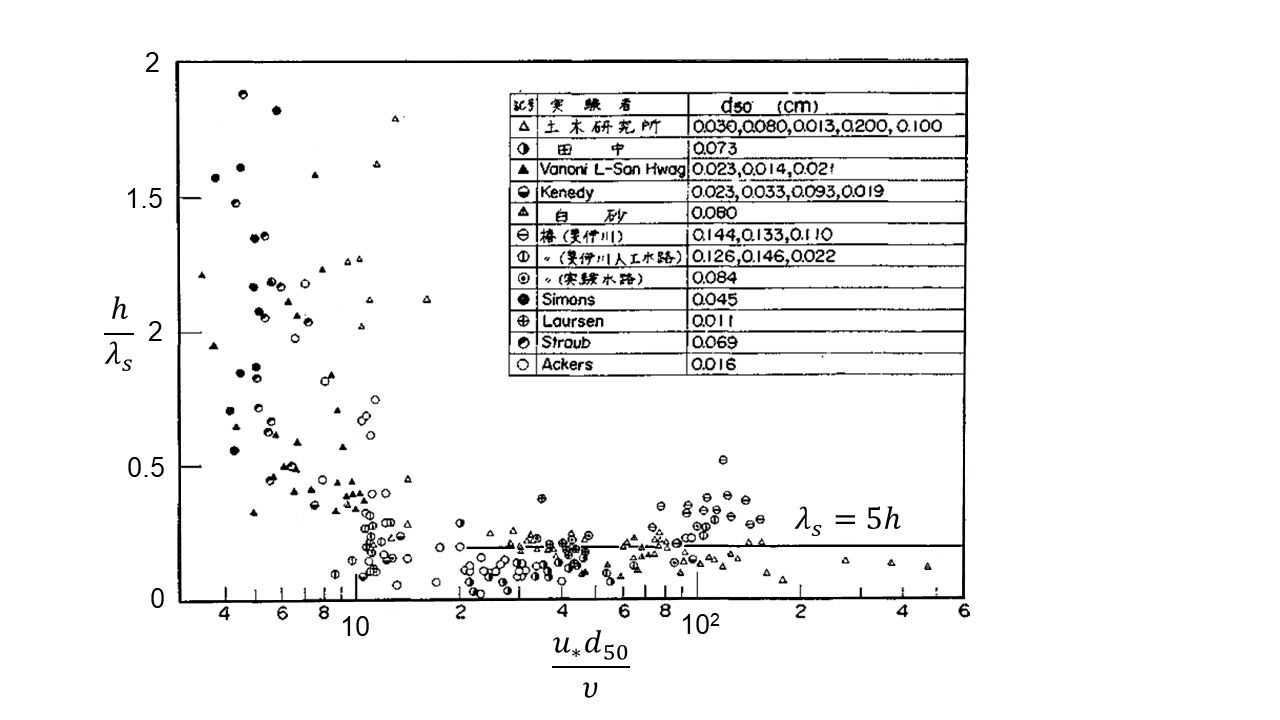
Figure 50 : 砂漣・砂堆に関する \(\cfrac{\Delta}{h}\) と \(\cfrac{u_\ast d_{50}}{\nu}\) の関係 (土木学会水理委員会[Ref:13]_ )

砂堆の波長 \(\lambda_s\) , 波高 \(\Delta_s\) については, Yalin [Ref:14] により次式が提案されています．

(198)\[\lambda_s = 5h\]

(199)\[\cfrac{\Delta_s}{h} =\cfrac{1}{6}\left(1-\cfrac{\tau_c}{\tau_0}\right)\]

ここで，\(\tau_0\) および \(\tau_c\) はそれぞれ掃流力および限界掃流力で, これらについては次節で説明します． Figure 50 より, (198) 式は成立していると見なせます． また, \(\Delta_s/h\) と \(\tau_c/\tau_0\) の関係は Figure 51 のようになっており，(199) 式の係数は \(1/6 \sim 1/2\) の範囲となっています．

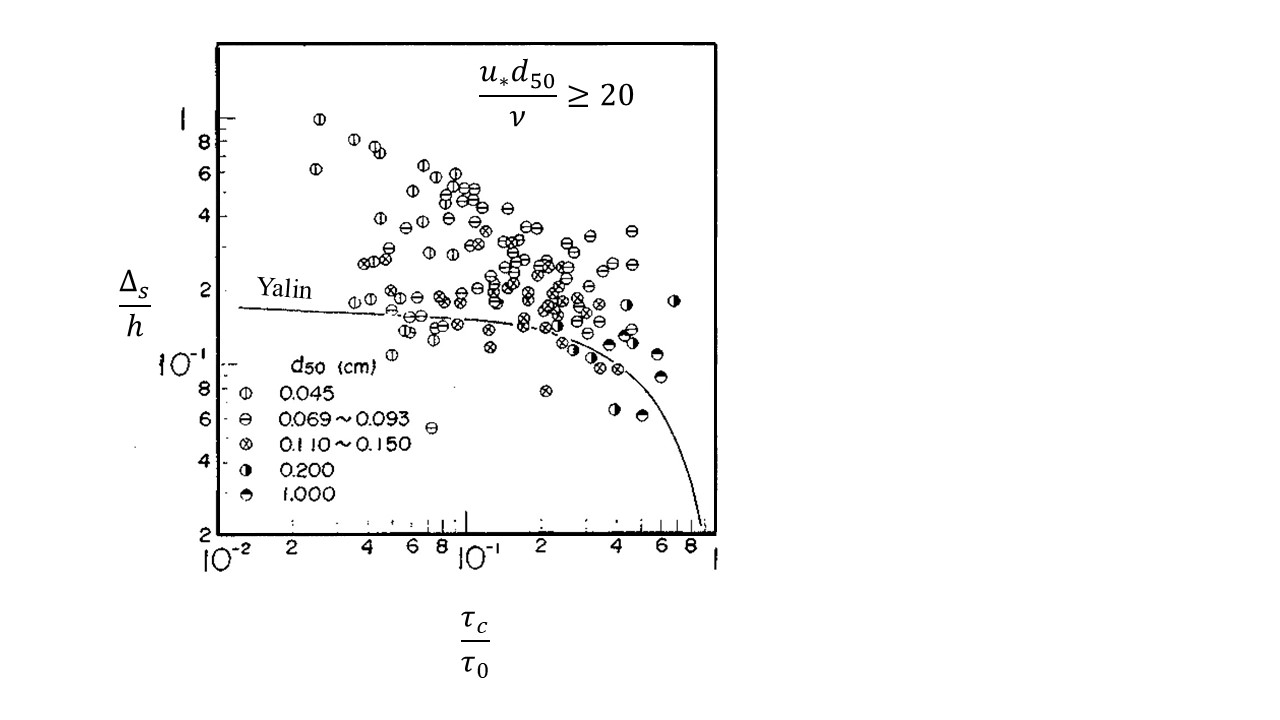
Figure 51 : 砂漣の \(\cfrac{\Delta_s}{h}\) と \(\cfrac{\tau_c}{\tau_0}\) の関係

(199) において \(\tau_0\) が \(\tau_c\) に比べて十分 に大きくなると,

(200)\[\cfrac{\Delta_s}{h} \rightarrow 1/6 = 0.166 \approx 0.2\]

となり，流砂が十分に流れている状態では砂堆(dune)の波高は水深の約20% に達するということになり, この状態で砂堆は一定の速度で移動します．

Figure 52 : 実験水路の砂堆の移動状況動画 [Ref:17]

Figure 52 は寒地土木研究所の伊波らによるduneの移動を記録した動画です([Ref:17])． 実験は, 水路幅0.5m, 勾配 1/500 の水路に平均粒径 d \(_m\) =0.515mm の均一粒径砂 を用いて行われ, 30 \(\ell/s\) の流量を流した場合の実験です，この動画の縦断方向の画角は約5.5mで， 動画から読み取った水深は約20cm, 砂堆の波長は約1m, 波高は約4cmとなり, (198) 式, (200) 式に合致していることが分かります．

砂漣(ripple)の波長と波高

一方, 砂漣の波長・波高は水深よりむしろ粒径に関係付けられ， 概ね以下のような関係があります. [Ref:13]

(201)\[\cfrac{\lambda_s}{d_{50}} = 300 \sim 1500 \Longrightarrow \mbox{平均で800程度}\]

(202)\[\cfrac{\Delta_s}{\lambda_s}= 1/5 \sim 1/200 \Longrightarrow \mbox{平均的で1/10程度}\]

中規模河床形態の基本特性

渡邊 [Ref:18] によると,中規模河床形態とは河床に形成される川幅規模の地形(来阿学模様)のことで， その形状から，(a)交互砂州(単列砂州), (b)複列砂に州, (c)多列砂州(網状砂州)に分類されます． 洗堀箇所と堆積箇所が現れ，これをきっかけに流れが蛇行し，さらにこの蛇行に起因する局所洗堀や河岸浸食が発生します． 従って河道の維持という観点から治水上重要な現象であるとともに瀬淵という河川環境上も重要な現象なので， 河川工学的に古くから注目されて来ました．

交互砂州(単列砂州)

交互砂州(単列砂州)が発生すると，流れが蛇行し, 左右岸交互に洗堀・堆積が生じ， 砂州の形状を表すような明確な前縁線が生じ，砂州は時間とともに下流に移動するように なります( Figure 53 )．

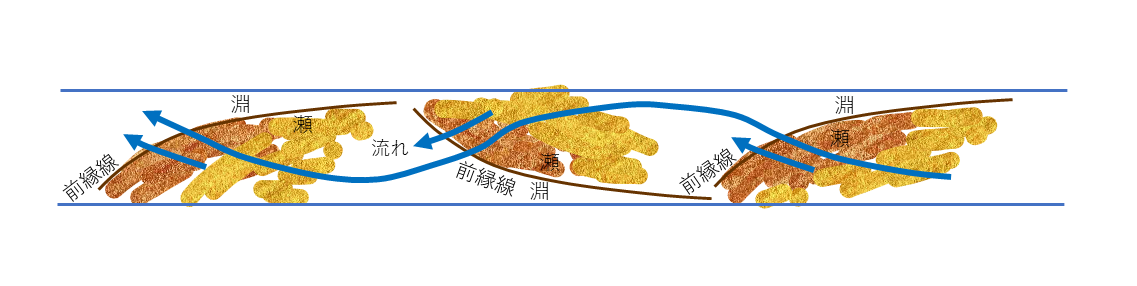
Figure 53 : 単列砂州の模式図

なお，北見工業大学の渡邊教授より前縁線について下記の説明を頂いております. [Ref:19]

注釈

砂州が形成される河床上を移動する流砂はある個所で移動を停止し，堆積肩を形成する． その堆積肩は，下図( Figure 54 )にみられるように、河床平面上で円弧状に存在し， その高さを増加させながら下流へと前進して，ある一定の高さまで発達します． 発達した後もこの円弧状の堆積肩は下流へと移動を続けます． この円弧状の堆積肩を砂州の 前縁線 と呼びます．

Figure 54 : 前縁線の定義図 [Ref:19]

Figure 55 は寒地土木研究所で行われた直線水路における交互砂州の移動状況を 鉛直上方から撮影した動画 [Ref:20] で, 水路幅 \(B=\) 0.9m, 勾配 \(i=\) 1/200, 河床材料平均 粒径 \(d_{50}=\) 0.77mm の水路に, 流量 \(Q=8 \ell\) /s を流した時の実験です．

Figure 55 : 直線水路おける交互砂州の移動状況の動画 [Ref:20]

Figure 56 は Figure 55 の実験と同じ条件で， iRICのNays2dH で計算したものです．計算結果も実験結果と同じような交互砂州が発生して移動しているのが分かります．

Figure 56 : 直線水路おける交互砂州の移動状況計算結果

那賀川

実河川の交互砂州は, Figure 57 の徳島県那賀川のものが有名です．

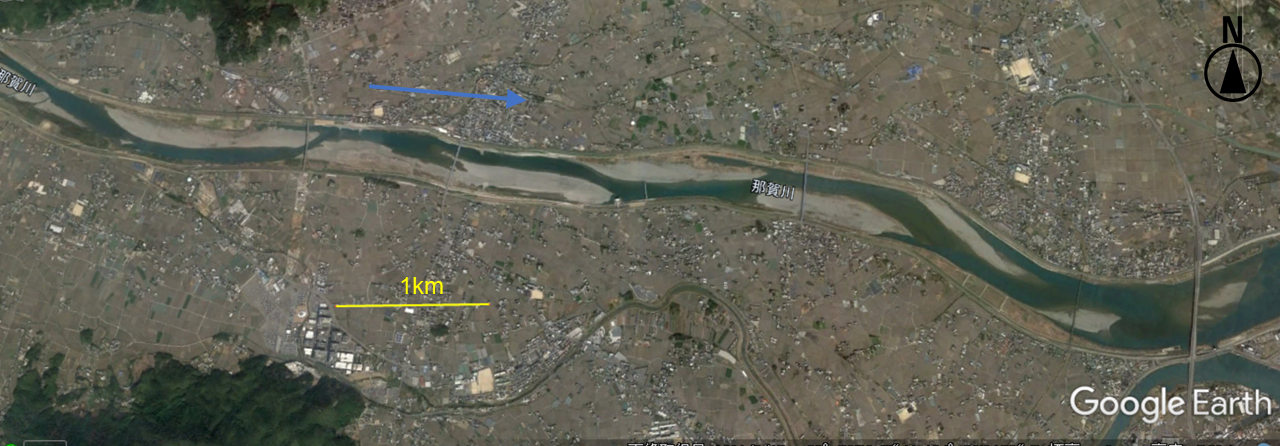
Figure 57 : 交互砂州の例(那賀川) Google Earthより

十勝川

十勝川の直線の新水路部にも Figure 58 のような綺麗な交互砂州が見られます．

Figure 58 : 交互砂州の例(十勝川)

十勝川の単列砂州ドーローン動画 (2021.11.09撮影)

複列砂州

単列砂州が横断方向に２列形成され，洗堀・堆積が縦断方向に両岸・中央の交互に形成され，流れは8の字を描くような状態を複列砂州と言います．複列砂州も下流へ移動しますが，その移動速度は単列砂州よりも遅くなります( Figure 59 )．

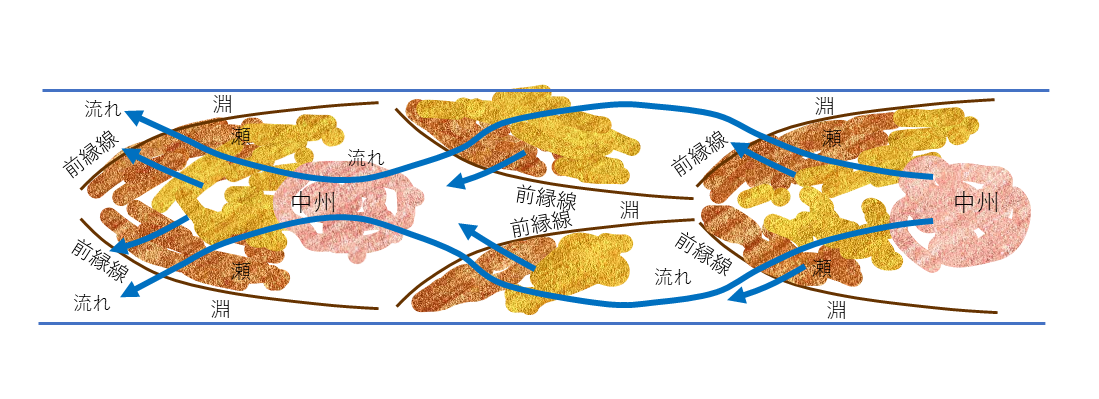
Figure 59 : 複列砂州模式図

庄川

Figure 60 は富山県の庄川に見られる複列砂州の例です．

Figure 60 : 複列砂州の例(庄川) Google Earth より

庄川複列砂州のドーローン撮影動画(2021年10月28日撮影)

札内川

こちらは, 札内川の複列砂州です．( Figure 61 )

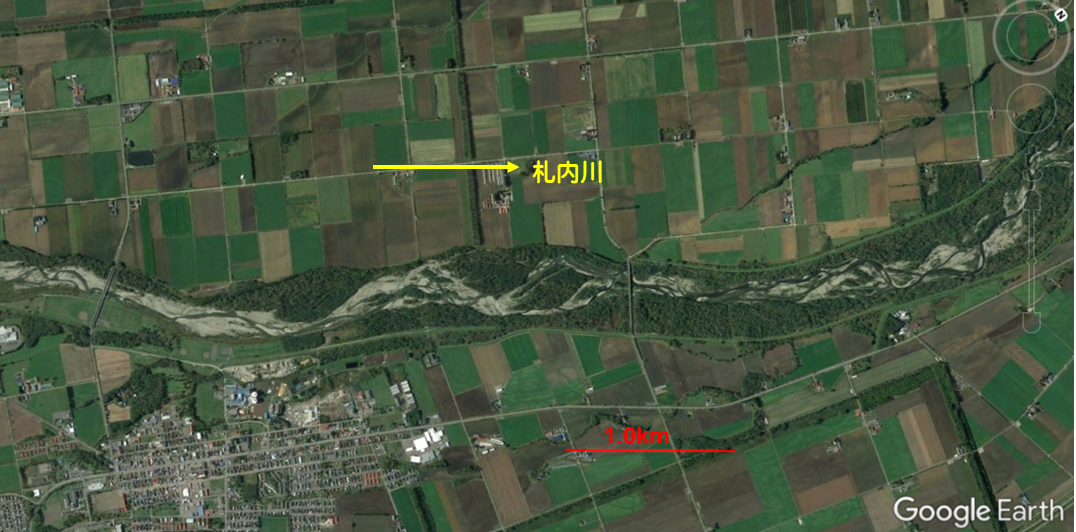
Figure 61 : 札内川の複列砂州河道部分

札内川複列砂州箇所のドローン映像(北海道開発局帯広開発建設部提供 2019年6月撮影)

札内川複列砂州箇所のドローン映像(北開水工コンサルタント提供 2021年11月撮影)

多列砂州(網状砂州・うろこ状砂州)

流路縦断方向の砂州の列数をモード数と言いいますが，モード数が3以上の砂州を多列砂州もしくは網状砂州，うろこ状砂州などと呼ばれます．

大井川

Figure 62 は静岡県 大井川の網状砂州の例，

Figure 62 :大井川の網状砂州 Google Earth より

大井川複列砂州のドローン映像(RiverLink 旭一岳氏 2022年9月撮影)

斐伊川

Figure 63 は島根県の斐伊川の網状砂州の例です．

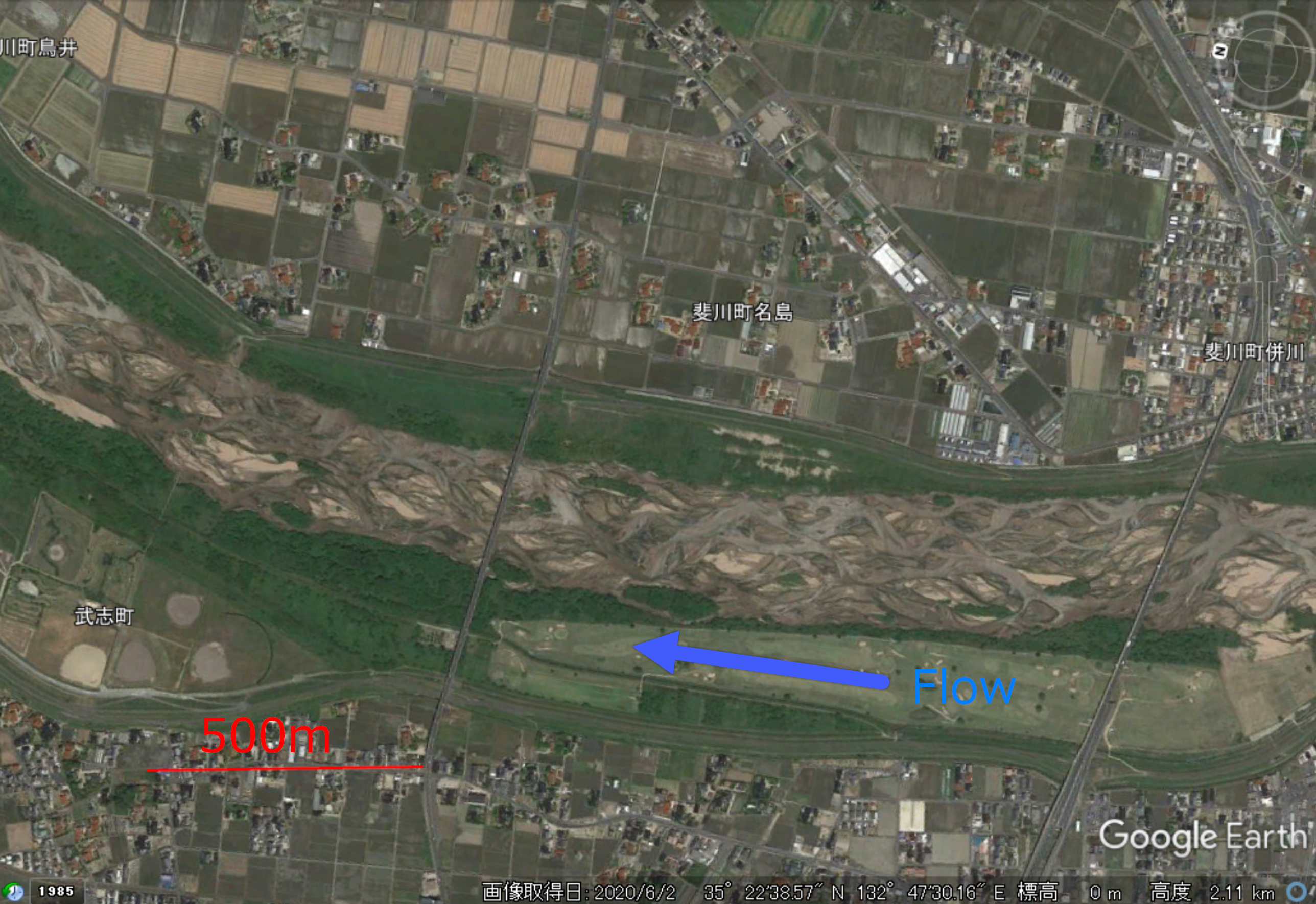
Figure 63 :斐伊川の網状砂州 Google Earth より

斐伊川複列砂州のドローン撮影動画 [Ref:36] (2021年12月3日撮影)

斐伊川のドローン空撮の静止画はこちらです.

世界の網状河川

他にも 世界中には沢山の美しい網状河川が存在してます.

中規模河床形態の領域区分

流路の形状的な条件と水理条件から，どのタイプの砂州が発生するかという発生領域区分に 関する研究は古くから多くの研究者により行われおり, 川幅・水深比( \(B/h\) )に依存する ことが知られてます． 理論的に解析する方法として，線形安定解析と呼ばれる方法があり, 黒木・岸 [Ref:21] による実用的な砂州発生の領域区分図が我が国では良く使われています． Figure 64 は実験水路データをこの領域区分図にプロットしたものです． ここで，横軸の \(\cfrac{BI^{0.2}}{h}\) というパラメータは通常の川幅・水深に若干の 勾配の影響を含ませることにより1つの領域区分図で広範囲の勾配の河川を同じ領域区分図で 分類するための工夫です． このパラーメタで用いられる川幅・水深は実験水路の場合は実験水路の川幅と平均水深となりますが，実河川においては低水路満杯流量，もしくは平均年最大流量時の水深およびそれに対応する水面幅を用いることが推奨されています．

Figure 64 :黒木・岸の中規模河床形態の領域区分(実験水路データとの比較) [Ref:21]

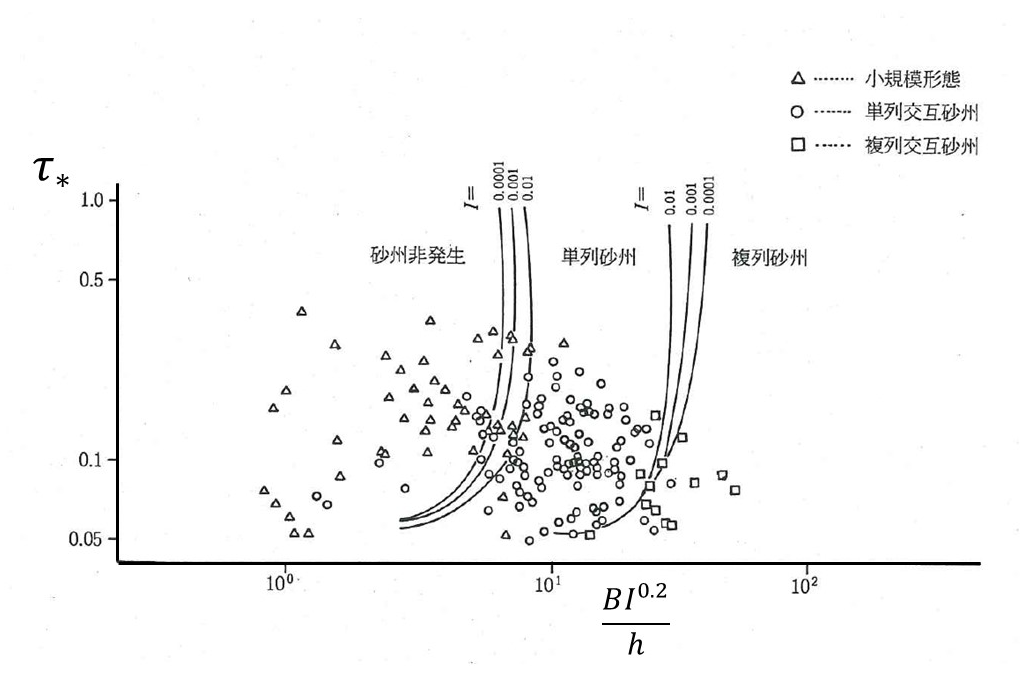
Figure 65 は山口・黒木[Ref:22]_ が実河川データーを領域区分図にプロットしたものです．

Figure 65 :黒木・岸の中規模河床形態の領域区分(実河川データとの比較) [Ref:22]

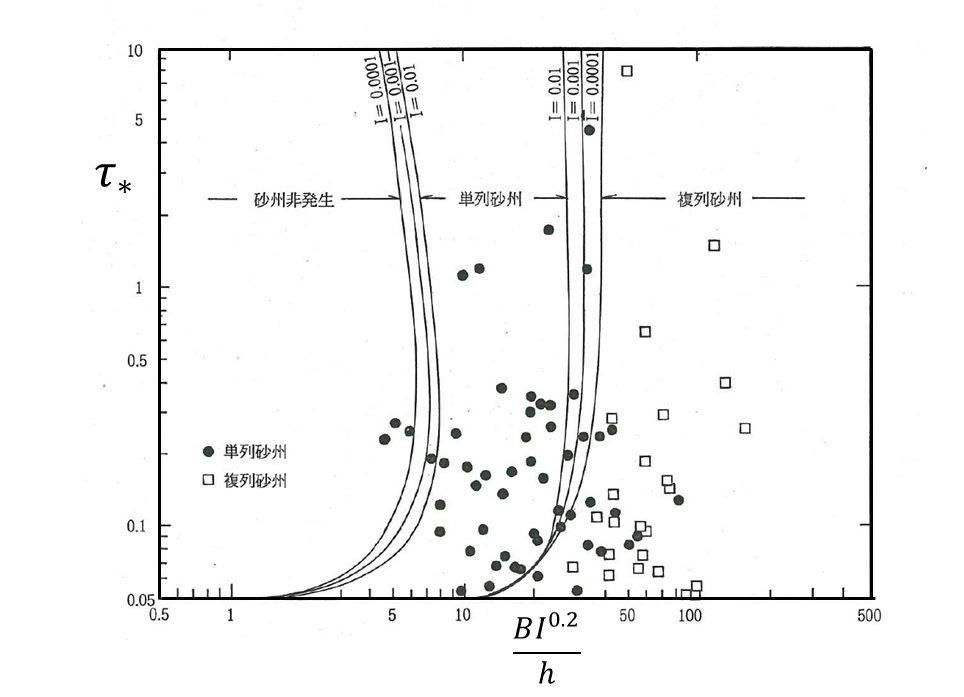
中規模河床形態の基本特性

中規模河床形態における砂州波長は，川幅(水路幅)との相関が高く, [Ref:13] による Figure 66 によれば,

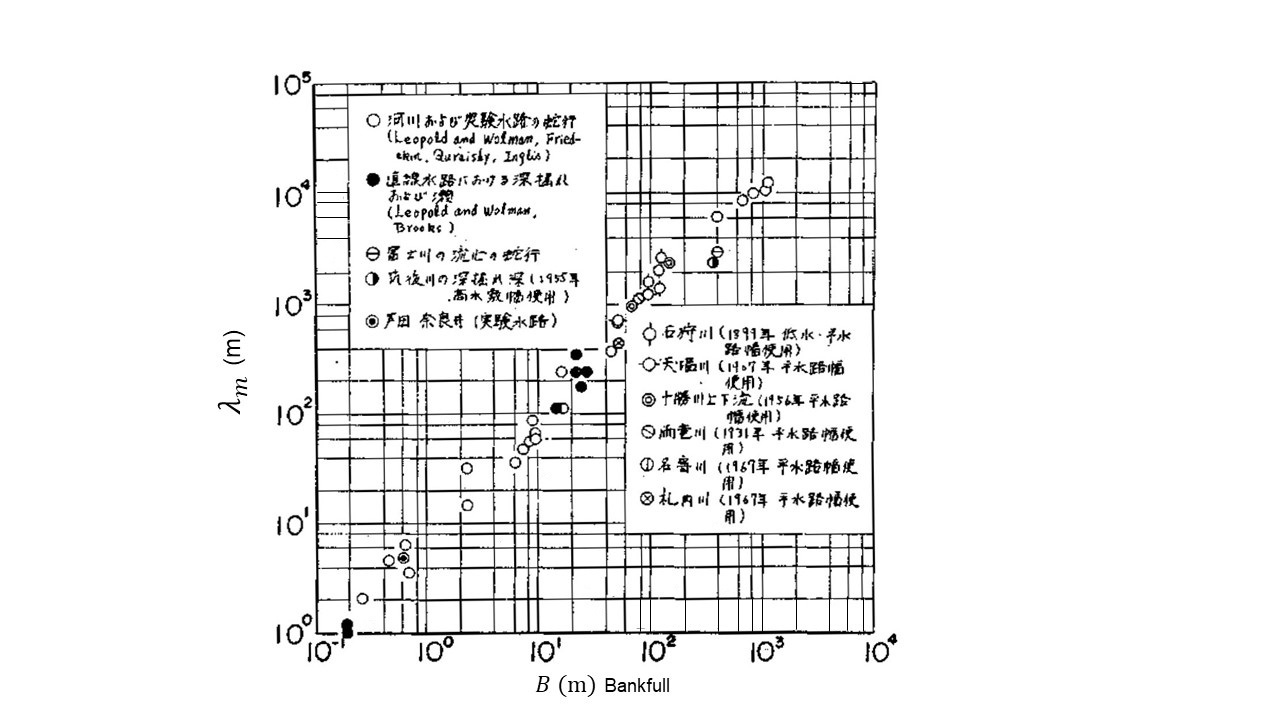
Figure 66 : 砂州の波長と川幅の関係

(203)\[\cfrac{\lambda_b}{B} = 7 \sim 15\]

の範囲に分布しています．ただし, \(\lambda_b\) は砂州波長, \(B\) は川幅であり，河川においては低水路満杯(Bankfull)時の川幅， 水路においては水路幅です． なお，ここでの砂州波長は後述の蛇行波長とは異なるので注意を要します．

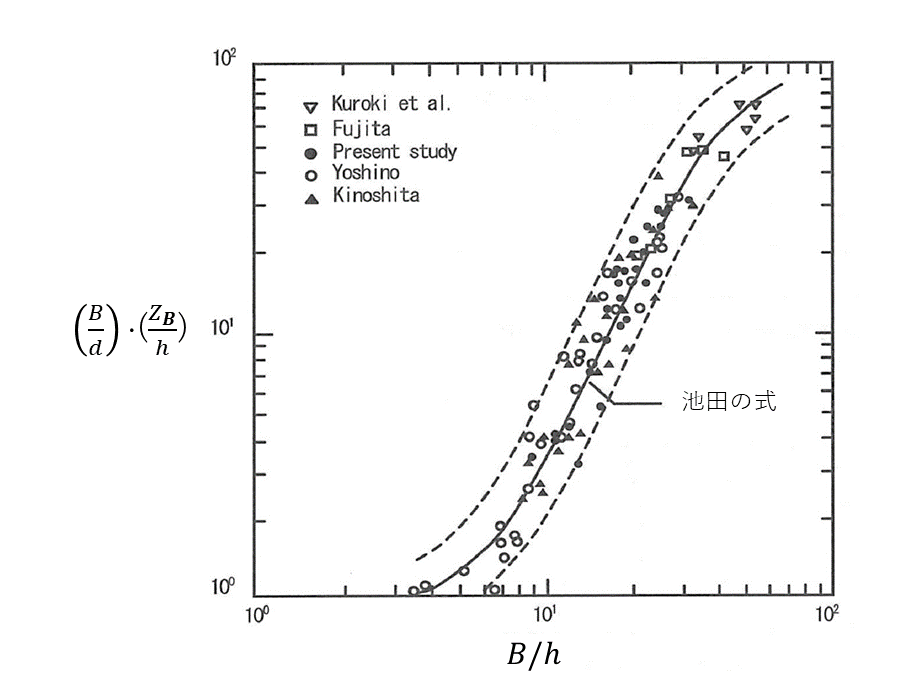
砂州波高についても \(B/h\) との相関性が高く，ここでは池田 [Ref:23] による 単列砂州の砂州波高式, (204) 式を紹介しておきます．

(204)\[\cfrac{Z_B}{h}=9.34\left(\cfrac{B}{d}\right)^{-0.45} \exp\left[2.53 \cdot \mbox{erf} \left \{ \cfrac{\log_{10}\left(\cfrac{B}{h}-1.22\right)}{0.594} \right\}\right]\]

ただし, \(Z_B\) は砂州波高, \(d\) は河床材料の粒径です．

Figure 67 : 砂州波高データーと池田 [Ref:23] の式

河川の平面形状と蛇行

沖積地の自然河川では，河岸が流れによって浸食を受けるので平面形状も変化します． 典型的な河川の平面形状は流路が左右に振れる蛇行現象です．河川に蛇行が起きる原因は， (1)平面形状そのものが持つ不安定性に起因する形状不安定説と (2)交互砂州が発生し， これによって河川の蛇行が始まるとする砂州起因説があります．

砂州起因による蛇行

河川に交互砂州が発生すると, 流れが左右に振れ, 浸食箇所も左右岸交互に現れるので, これをきっかけに流路そのものが左右に蛇行し始めます． Figure 68 は木下 [Ref:24] による砂州から蛇行河道, さらに蛇行の度合いが 大きい迂曲河道と呼ばれる平面形状に至る様子を表した模式図です．

Figure 68 : 木下 [Ref:24] による砂州から蛇行の説明図

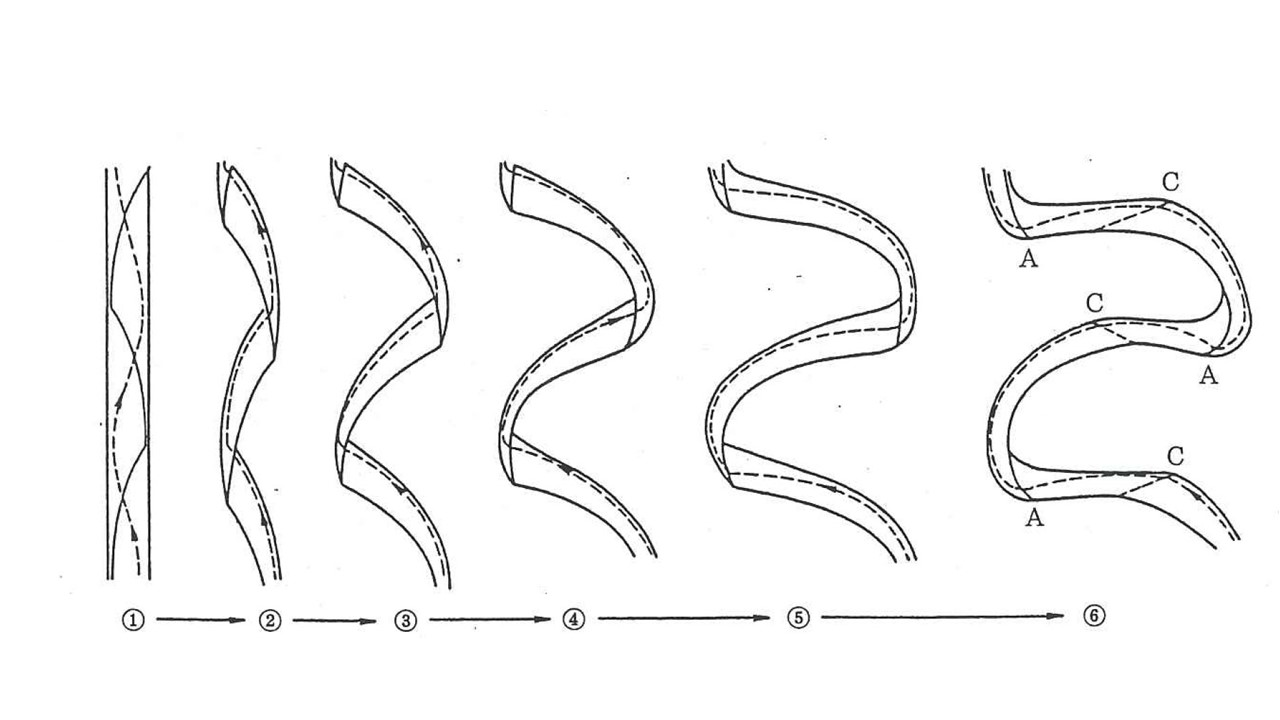
以下は木下 [Ref:24] による蛇行の発達過程の説明です．

• 直線河道に交互砂州が形成され,水流が蛇行する. (単列と複列がある)

• 蛇行の初期には1蛇行は砂州2個から成り立っており,このときの流心は凹岸側下流へ寄っていき,流路の蛇行は下流へ向って移動する. (蛇曲河道)

• 蛇行の進行とともに, 1蛇行内の砂州は2個から3個となり, 流心は凹岸側下流以外に横, 上流へも寄ることができ, 横方向, 上流方向への蛇行平面形状の発達が可能となる. これとともに⓺のA地点のような袂状部が形成される. (迂曲河道)

• やがてはA地点付近が不動点となり，前進する蛇行河道に追いつかれ，遂には自然短絡に至る.

蛇行が著しくなり，蛇行1波長内に1対より多くの砂州が形成さる状態を迂曲河道と呼ばれます． この時，砂州による流線蛇行の曲頂部が河道平面形の外岸部になる場合をB型接続, 内岸部になる場合をC型接続と言い, B型接続の状態ではまだ蛇行は発達するが, C型接続になるとその部分の蛇行発達できなくなります( Figure 69 ).

Figure 69 : 迂曲河道の砂州の接続形態(図は渡邊による [Ref:18] から転記)

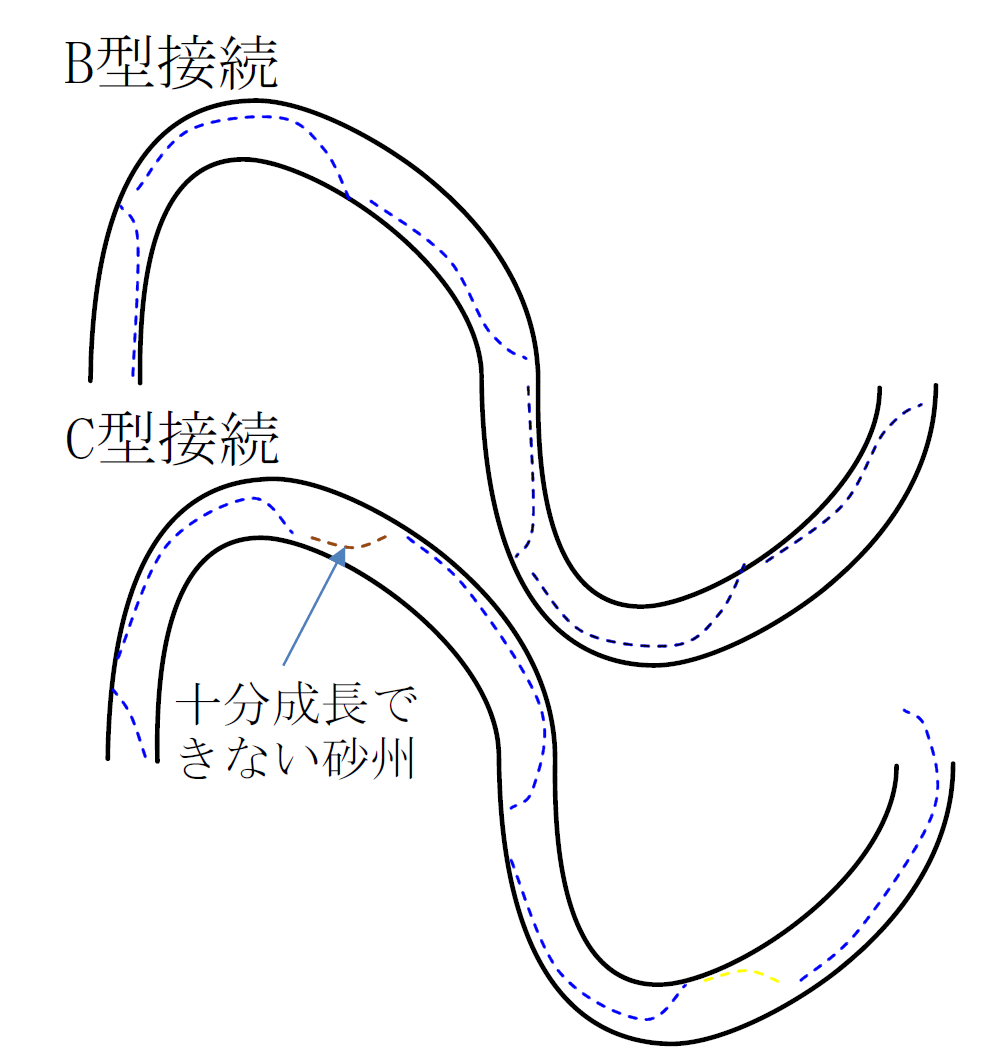
平面形状の不安定による蛇行

池田ら [Ref:25] は蛇行による偏倚流速を平面変動の駆動力と考え，Engelund による蛇行流の理論解を用いて平面不安定の発生条件，卓越波長を導き，ゆわゆる蛇行の平面形状平面不安定説の最初の研究となりました．その後，同様な平面形状の不安定に基づく蛇行に関する研究が異なる研究者によって進められて来たが，上記の砂州の影響は含まれておらす，その後の研究では砂州の影響が無くても蛇行は発達するという報告も行われています( [Ref:26] )

自由砂州と固定砂州

ここまでの説明では砂州は単列砂州と複列砂州に分類されていますが, 砂州の分類法としてもう一つ別の分類法があります． これは, 自由砂州(free bar)と固定砂州(point bar)という分類で, 自由砂州とは，直線もしくは比較的直線に近い河川において発生し，下流へ向かって自由に移動する砂州で, 固定砂州とはは河川の平面形状(蛇行形状)に規定され，湾曲部の内岸側に発生して，位置が固定さた砂州のことです．

前記の寒地土木研究所の実験( Figure 55 )やその計算( Figure 56 )は見ての通り移動してますので自由砂州です． また，那賀川の交互砂州( Figure 57 )や, 庄川( Figure 60), 斐伊川( Figure 63 )の複列砂州の例も自由砂州と思われます．

砂州の移動限界蛇行角

木下 [Ref:24] によれば，Figure 70 に示すように, 図中に示される \(\theta\) (蛇行角)がある限界値を超えると砂州の前進が停止し，交互砂州と 固定砂州が合体した形の砂州となるとされています．

Figure 70 : 砂州の停止限界蛇行角 (木下 [Ref:24] )

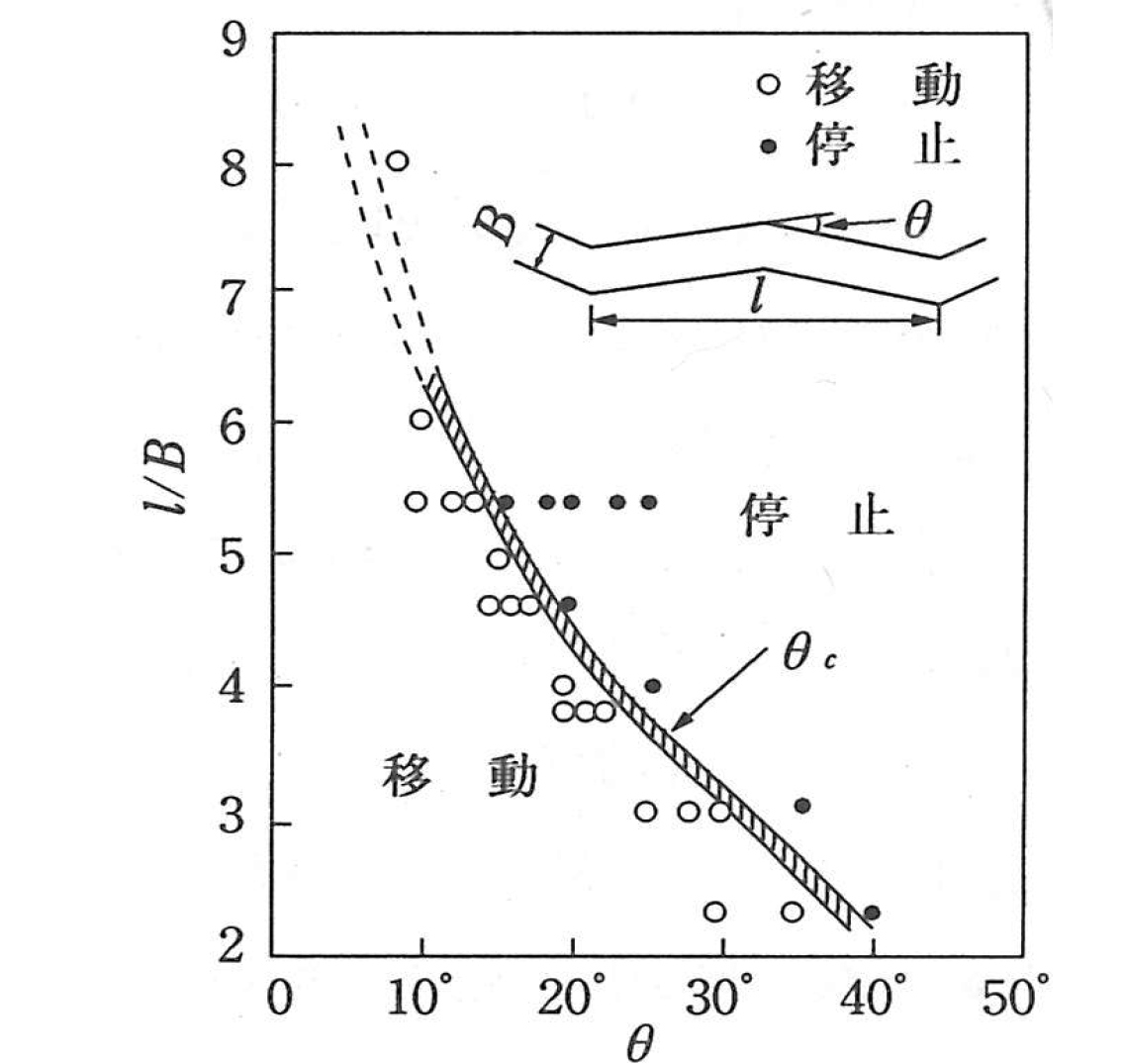
Figure 70 における蛇行角の定義はジグザク水路のものであるが， 一般河川の場合の蛇行角は Figure 71 に示すように，谷軸方向と 流路中心線の方向の角度が最大となる地点の角度として定義され， 蛇行角もしくは最大蛇行角と呼ばれます．

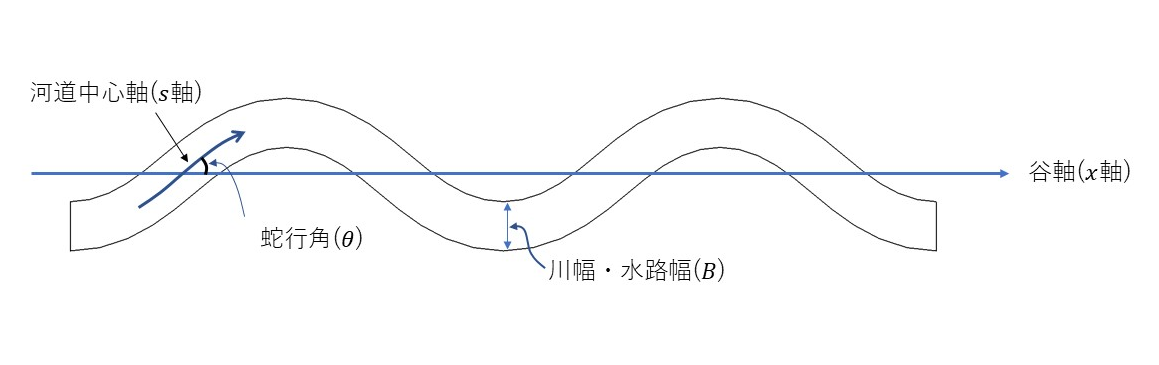
Figure 71 : 蛇行角の定義

以下の Figure 72 \(\sim\) Figure 75 は同じ水理条件で蛇行角のみを \(0^{\circ} \sim 30^{\circ}\) で変化させた場合の河床変動シミュレーション結果です． 直線水路では自由に下流へ移動する砂州が，蛇行角が増加する毎に地形に拘束されるような形で 鈍くなり，Figure 75 の \(30^{\circ}\) では完全に停止してしまうのが分かります． 木下 [Ref: 24]_ の指摘に一致しているのが分かります．なお，ここでの計算モデルは iRIC のNays2dHで， 水理条件は長谷川 [Ref:27] による 直線水路・交互砂州の実験と同じものです．

Figure 72 : 直線水路における砂州移動シミュレーション

Figure 73 : 蛇行角 \(\theta=10^{\circ}\) の場合の砂州移動シミュレーション

Figure 74 : 蛇行角 \(\theta=20^{\circ}\) の場合の砂州移動シミュレーション

Figure 75 : 蛇行角 \(\theta=30^{\circ}\) の場合の砂州移動シミュレーション

節腹連続河道

(A)非砂州, (B)単列砂州, (C)複列砂州と(1)自由砂州と(2)固定砂州，3×2の組み合わせで6通りの中規模河床形態が存在するのかどうかというのは興味深い所い点です．これはまだ未解決の分野ではありますが，

まず(B-1), (C-1)は流路が直線に近く, 水理条件が発生領域にさえ入っていれば発生することは容易に想像されます．（ただし，特に複列の自由砂州の場合，その状態で動的定常状態まで続くのかとうかという点については議論の余地があります.) 次に(B-2)は上記の交互砂州が蛇行角が大きくなると平面形状にトラップされてしまう例で，この場合は自由砂州と固定砂州が共存している状態だと思います．問題は(C-2)が存在するのかという点ですが，これは渡邊ら [Ref:28] や 山口・渡邊 [Ref:29] による 節腹連続河道 に相当するようで, 自然河川でも斐伊川や札内川で見られるとのことです．

Figure 76 : 斐伊川河口部の節腹河道部(2021年12月4日 出雲空港離陸直後のJAL機より撮影)

河川の平面蛇行の実例

自然河川ほぼすべて蛇行しているので，Google Earthなどで蛇行河川を探すのは極めて容易です． 例えば，

四万十川

Figure 77 : 高知県 四万十川の蛇行と固定砂州

空知川

Figure 78 : 空知川 湾曲部の固定砂州

最近では，過去数十年におよぶ蛇行河川の平面形状の変遷を Google Earth Engine で誰でも調べることが可能となっており，以下のような平面形状変化の可視化が可能となっています．

Ukayari川

Figure 79 : アマゾン川上流Ukayari川(ペルー)の自由蛇行

Ichilo川

アマゾン川上流，ボリビア国内河川の30年間の蛇行の様子(Google Earth Engineにより作成) [Ref:16]

最近では自由蛇行の長期間の時間変動をシミュレーションすることも可能になって来てます． Figure 80 はAsahiら [Ref:30] による自由蛇行の数値シミュレーション結果です．

Figure 80 : 自由蛇行のシミュレーション(Asahiら [Ref:30] )

掃流力と限界掃流力

開水路に水が流れている場合，流れによって河床が流体によって押される力(せん断力)が生じます． この力を 掃流力 と呼びます． Figure 81 図に示すように，勾配 \(i\) の水路に 水深 \(h\) で水が等流状態で流れている時，流れ方向に長さが1, 横断方向に長さが1の水塊 に働く重量 \(W\) は \(W=\rho gh\) で，この斜面方向成分 \(T\) は \(T=\rho g h \sin(i) \approx \rho ghi\) です．ただし, \(g\) は重力加速度, \(\rho\) は流体の密度です.

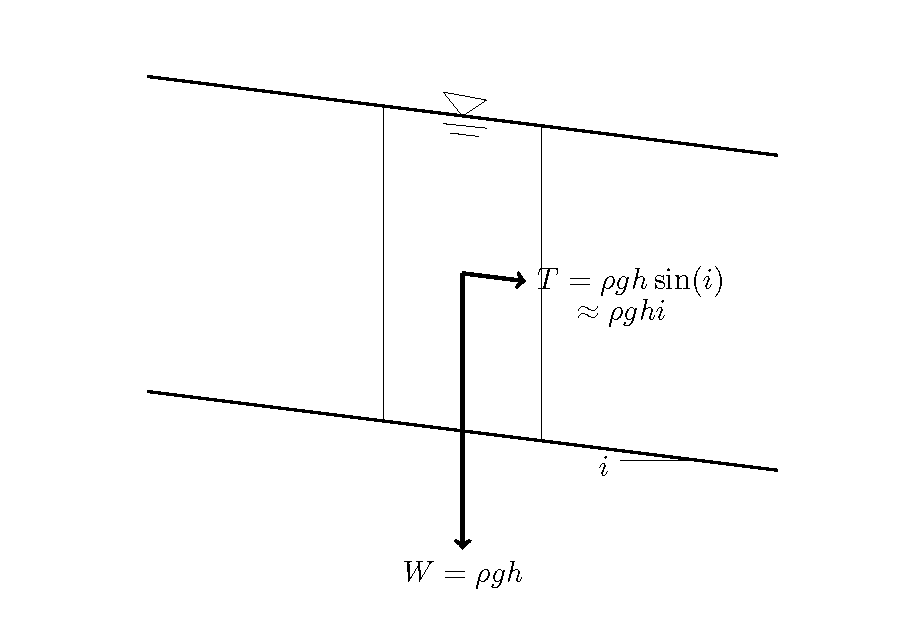
Figure 81 : 掃流力の定義

この時の 掃流力 を \(\tau_0\) とすると \(\tau_0\) は単位面積あたりの \(T\) なので，

(205)\[\tau_0 = \rho ghi\]

となります．なお．一般的には (205) 式の水深 \(h\) は径深 \(R\) を用いる のが正しい表現ですが，広長方形断面の水路や，二次元計算において各セルの代表する水深という 意味ではそのまま \(h\) を用います． なお，等流状態で無い場合（例えば不等流や不定流）には掃流力は (205) において \(i\) の替わりにエネルギー勾配 \(I_e\) を用いて算定されます． したがって，一次元流れでマニング則を適用する場合には，掃流力は次式で表されます．

(206)\[\cfrac{\tau_0}{\rho} = ghI_e = \cfrac{g n_m^2 <u>^2}{h^{1/3}}\]

ただし, \(n_m\) はマニングの粗度係数, \(<u>\) は水深平均流速です． 河床が一様粒径の砂で構成されている場合， \(\tau_0\) を次式で無次元化した値は 無次元掃流力 または シールズ数 と呼ばれ， 土砂水理学で頻繁に使用される重要なパラメーターです．

(207)\[\tau_\ast = \cfrac{\tau_0}{\rho s g d} = \cfrac{h I_e}{s d}\]

ただし, \(s\) は砂粒子の水中比重, \(d\) は砂の粒径です． また，掃流力を次式のように流速の次元で表したものを 摩擦速度 といい，通常 \(u_*\) で表します．

(208)\[u_\ast=\sqrt{\cfrac{\tau_o}{\rho}}=\sqrt{g h I_e}\]

したがって，掃流力 \(\tau_0\) は

(209)\[\tau_0 = \rho {u_\ast}^2\]

と書くことが出来ます．摩擦速度はその名前から流速の一種のようにとらえられがちですが， 流速ではなく，あくまでも「掃流力を速度の次元で表したもの」ということです．

流砂の分類

河川の流砂は，河床材料と交換されながら輸送される Bed Material Load と 交換されずに上流から来たものがそのまま下流に輸送される Wash Load に分類されます． また， Bed Material Load のうち，河床付近を転動，滑動や跳躍をしながら輸送される成分を 掃流砂 , 乱れによる拡散の影響を受けながら流水中を輸送される成分を 浮遊砂 と呼びます． 本テキストでは主として Bed Material Load のうちの 掃流砂 と 浮遊砂 を扱います．

掃流砂の移動限界

ある砂粒子が河床上にある時，河床における掃流力 \(\tau_0\) あるいは 摩擦速度 \(u_\ast\) がある値を超えると移動を開始するとした場合， その限界のことを移動限界，限界値のことを 限界掃流力 \(\tau_c\) , その時の あるいは 限界摩擦速度 \(u_{\ast c}\) といいます．したがって河床砂粒子が移動するかどうかについては，\(\tau_c\) あるいは \(u_{\ast c}\) を用いて以下のように表されます．

(210)\[\begin{split}u_\ast < u_{\ast c} \; \; \; & \mbox{または} \; \; \; & \tau_0 < \tau_c \; \; \mbox{静止}\\ u_\ast > u_{\ast c} \; \; \; & \mbox{または} \; \; \; & \tau_0 > \tau_c \; \; \mbox{移動}\end{split}\]

限界掃流力も掃流力と同様に通常は次式の無次元の形で表され， 無次元限界掃流力 と呼ばれます．

(211)\[\tau_{\ast c}= \cfrac{\tau_c}{\rho s g d} = \cfrac{{u_{\ast c}}^2}{sgd} = \cfrac{\tau_c}{\rho s g d}\]

前節の (199) で用いられている \(\tau_c\) は上式で表されます．

均一粒径河床材料の限界摩擦速度については次式で表される岩垣の式 [Ref:5] が良く持ちいられます.

(212)\[\begin{split}d \geq 0.303 \mbox{cm}: & \; \; {u_{\ast c}}^2 = 80.9d \\ 0.118 \leq d \leq 0.303 \mbox{cm}: & \; \; {u_{\ast c}}^2 = 134.6 d^{31/22} \\ 0.0565 \leq d \leq 0.118 \mbox{cm}: & \; \; {u_{\ast c}}^2 = 55d \\ 0.0065 \leq d \leq 0.0565 \mbox{cm}: & \; \; {u_{\ast c}}^2 =8.41d^{11/22} \\ d \leq 0.0065 \mbox{cm}: & \; \; {u_{\ast c}}^2 = 226d\end{split}\]

ただし, ここでの \(d\) はcm単位の粒径で, \(u_{\ast c}\) の単位は cm/s です.

浮遊砂の浮上・沈降速度と存在可能領域

掃流砂の掃流限界に対して，浮遊砂は浮上するかしないかの 浮上限界 という概念が重要になる. 浮上限界は，浮上速度と沈降速度の大小関係によって決まります．沈降速度 として代表的な ものとして次式のRubeyの式 [Ref:6] が挙げられます．

(213)\[\cfrac{w_f}{\sqrt{sgd}}=\sqrt{\cfrac{2}{3}+\cfrac{36\nu^2}{sgd^3}} -\sqrt{\cfrac{36\nu^2}{sgd^3}}\]

一方，砂粒子の移動速度は摩擦速度に比例するといわれており, \(u_s\) を移動速度として, 次の関係があるとされています．

(214)\[u_s=0.6 u_\ast \sim 0.93 u_\ast\]

乱流中の砂粒子の移動は水平方向にも鉛直方向にも生じますので，

(215)\[\begin{split}u_s > w_f \; \; & \mbox{のとき浮上} \\ u_s < w_f \; \; & \mbox{のとき沈降}\end{split}\]

の関係を仮定すると, 浮上限界は,

(216)\[\cfrac{u_s}{w_f}=0.6 \cfrac{u_\ast}{w_f} \sim 0.93 \cfrac{u_\ast}{w_f}=1\]

より,

(217)\[1.08 \sim \cfrac{u_\ast}{w_f} \sim 1.67\]

となり，これを用いて以下のように掃流砂と浮遊砂の存在領域の区分を行うと 次式となります．

(218)\[\begin{split}\mbox{掃流砂領域:} \; \; & \cfrac{u_\ast}{w_f} < 1.08 \\ \mbox{混在領域:} \; \; & 1.08 < \cfrac{u_\ast}{w_f} < 1.67 \\ \mbox{浮遊砂領域} \; \; & 1.67 < \cfrac{u_\ast}{w_f}\end{split}\]

なお，掃流砂の存在は (218) 式と同時に (210) 式の移動条件も 満たさなければならないので，これらを用いて，移動床流れにおける流砂の状態を 判断することが可能となります．

掃流砂量式

河床材料が十分に存在し，河床粒子の移動が 平衡状態に達した状態での流砂量を表す式を平衡状態掃流砂量式，もしくは単に掃流砂量式と言います． 掃流砂量式は古くから数多く提案されて来ていますが，ここでは河床変動計算に多用される 代表的なものを紹介します．

Meyer-Peter-Muller式

古典的な式ですが，式形が単純であり比較的適合性も高いため，河床変動計算では良く用いられる 式として，Mayer-Peter-Mullerの式(MPM式) [Ref:7] があります．

(219)\[\cfrac{q_b}{\sqrt{sgd^3}}= 8(\tau_\ast - \tau_{\ast c})^{3/2}\]

ただし，\(q_b\) は単位幅掃流砂量です．

芦田・道上の式

より理論的な考察に基づいて導かれた以下の芦田・道上の式 [Ref:8] も， 優れた掃流砂量式として広く用いられています．

(220)\[\cfrac{q_b}{\sqrt{sgd^3}}=17 {\tau_{\ast e}}^{3/2} \left( 1-\cfrac{\tau_{\ast c}}{\tau_\ast} \right) \left( 1-\cfrac{u_{\ast c}}{u_\ast} \right)\]

ここで, \(\tau_{\ast e}\) は有効掃流力で, 掃流力のうちの 実質的に河床材料に作用する掃流力の無次元表示であり，次式で表されます．

(221)\[\tau_{\ast e}= \cfrac{{u_{\ast e}}^2}{sgd}\]

ただし, \(u_{\ast e}\) は有効摩擦速度であり, 芦田・道上 [Ref:8] によれば, 次式で表されます.

(222)\[\cfrac{<u>}{u_{\ast e}}=6.0+5.75 \log_{10} \cfrac{h}{d(1+2\tau_\ast)}\]

浮遊砂量

一般に浮遊砂を含む河川流の問題は非常に複雑ですが，ここでは浮遊砂問題を河床変動計算 に取り込むために必要最小限の知識を簡単に説明します．

浮遊砂の定義と浮遊砂量

流水中の浮遊砂濃度 \(c\) は流水中の単位体積流体中の浮遊物質の体積として， 次式で表されます．

(223)\[c=\cfrac{V_s}{V}\]

ただし，\(V\) は流体の単位体積(=1), \(V_s\) は単位体積中の浮遊物質の体積です． 従って浮遊砂濃度の次元は[体積]/[体積]で無次元ということになります．

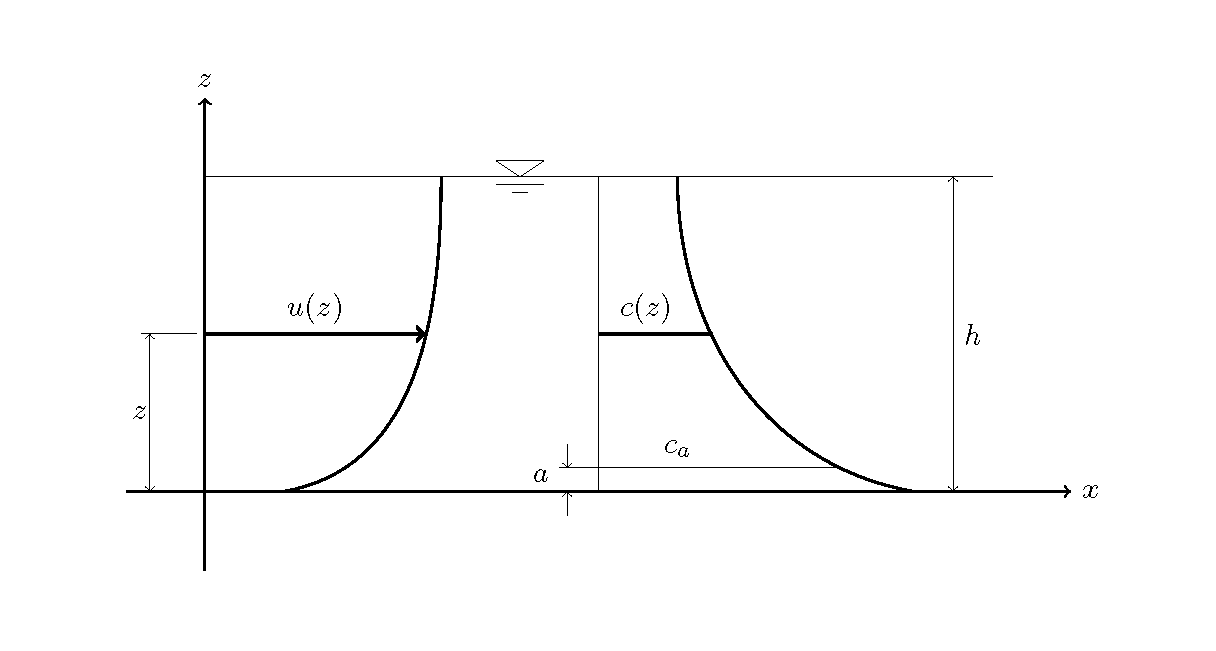
Figure 82 : 流速分布および濃度分布

Figure 82 のようにな鉛直2次元流を想定した場合, 単位幅当りの浮遊砂量 \(q_s\) は，鉛直方向の濃度分布 \(c(z)\) および鉛直方向の流速分布 \(u(z)\) が与えられれば次式で求めることが出来ます． 鉛直方向流速分布については[ 流速分布について ]を参照してください．

(224)\[q_s=\int^h_a c(z)u(z)dz\]

ここに, \(h\) は水深, \(c(z)\) および \(u(z)\) はそれぞれ河床から \(z\) の高さにおける浮遊砂濃度および流速, \(a\) は濃度の基準点とされる点の河床からの高さです．

ただし，本テキストで対象としている1次元計算や，平面２次元計算においては，流速も浮遊砂濃度も 水深平均値で計算するため，例えば2次元計算では, \(q_s\) は近似的に次式で表されます．

(225)\[q_s=<c>u\]

ただし, \(<c>\) は水深平均の浮遊砂濃度, \(u\) は水深平均流速です． \(<c>\) については平面2次元計算の場合は2次元の移流拡散方程式から求めます．

1次元計算の場合，浮遊砂量は単位幅ではなく，断面全体の平均浮遊砂量を対象とするため， 次式で計算されます．

(226)\[Q_s=<c>Q\]

ここでは \(<c>\) は断面平均濃度, \(Q\) は流量となります．

なお，1次元計算でも2次元計算でも，河床変動計算を行う場合は, 浮遊砂量そのものよりも， Figure 83 に示すように，河床(もしくは河床近傍)における 浮遊砂の浮上量 と， 浮遊砂の沈降量 の差によって河床変動が決まるので，これらの量が重要になります．

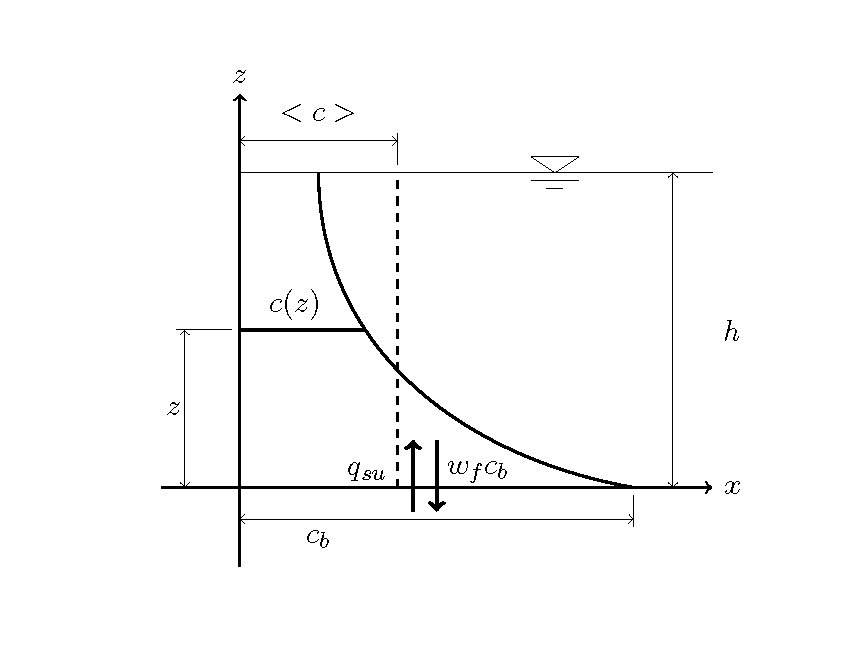
Figure 83 : 浮遊砂の浮上と沈降

ここで，河床への沈降量は，沈降速度と河床近傍の濃度の積(= \(w_f c_b\) )として表され, \(c_b\) については数値計算で求まるその場所の水深平均濃度 \(<c>\) から 鉛直方向の濃度分布式を用いて求めます． 一方, 浮上量は浮遊砂の浮上量(= \(q_{su}\) )として表されますが, こちらはその場所の 掃流力から計算されます．従って，その場の掃流力から計算される浮上量と時空間分布として計算される 沈降量の差によって河床高の変化が計算されるということになります． 以下に，浮上量と鉛直方向の濃度分布式の算出方法の例を示します．

浮遊砂の基準点濃度と浮上量式

浮上量は次式で表されます．

(227)\[q_{su}= w_f c_a\]

ただし, \(q_{su}\) は河床単位面積当たりの浮遊砂の浮上量で前述のように，その場所の掃流力から 局所的な平衡状態を仮定して得られる値であり, \(c_a\) は平衡浮上量に対応する平衡状態濃度です． 基準点濃度 \(c_a\) については，様々な式が提案されていますが(例えば [Ref:9])，ここでは， Itakura and Kishi [Ref:10] の式を紹介します．

(228)\[c_a = K\left( \alpha_\ast \cfrac{\rho_s-\rho}{\rho_s} \cfrac{gd}{u_\ast w_f} \Omega-1\right)\]

ただし, \(K=0.008\) , \(\alpha_\ast=0.14\) , \(\rho_s\) は 砂粒子の密度, \(\Omega\) は,

(229)\[\Omega = \cfrac{\tau_\ast}{B_\ast} \cfrac{ \displaystyle\int^\infty_{a'} \xi \cfrac{1}{\sqrt{\pi}}\exp(\xi^2)d\xi }{ \displaystyle\int^\infty_{a'} \cfrac{1}{\sqrt{\pi}}\exp(\xi^2)d\xi } +\cfrac{\tau_\ast}{B_\ast \eta_0}-1\]

です．ここで, \(\eta_0=0.5\), \(B_\ast=0.143\), \(a'=\cfrac{B_\ast}{\tau_\ast}-\cfrac{1}{\eta_0}\) です． なお，Itakura and Kishi [Ref:10] の式では，基準点の高さは \(a=0.05h\) とされています．

基準点濃度を \(c_a\) が与えられると, 平衡状態(浮上量と沈降量が一致した状態)における浮遊砂の浮上量 は (227) 式で求めることが出来ます. なお，(227) を \(\sqrt{sgd}\) で除して無次元表示すると，浮上量は次式となります．

(230)\[\cfrac{q_{su}}{\sqrt{sgd}}= K\left( \alpha_\ast \cfrac{\rho}{\rho_s} \cfrac{\Omega}{\sqrt{\tau_\ast}}-\cfrac{w_f}{\sqrt{sgd}} \right)\]

なお．(230) 式中の \(\Omega\) は (229) に示したように複雑な形式を しているので計算がめんどうですが，近似式 [Ref:11] を用いることにより計算が簡単になり， Itakura and Kishi [Ref:10] による浮上量式は近似的に次式とすることも可能です．

(231)\[\cfrac{q_{su}}{\sqrt{sgd}}=0.008 \left\{ 0.14\cfrac{\rho}{\rho_s}\left( 14\sqrt{\tau_\ast}-\cfrac{0.9}{\sqrt{\tau_\ast}}\right) -\cfrac{w_f}{\sqrt{sgd}}\right\}\]

濃度分布式と水深平均濃度

定常等流状態における水深方向の浮遊砂濃度の拡散方程式を次式で与えます．

(232)\[\cfrac{\partial}{\partial z} \left( \epsilon \cfrac{\partial c}{\partial z} \right)+ w_f \cfrac{\partial c}{\partial z}=0\]

ただし, \(\epsilon\) は水深方向の浮遊砂の拡散係数です． 沈降速度 \(w_f\) は水深方向に一定とし, (232) を \(z\) に関して積分し, 水面から粒子が飛び出さない条件を考慮すると，次式が得られます．

(233)\[\epsilon \cfrac{\partial c}{\partial z}+w_f c =0\]

\(\epsilon\) も水深方向に一定とし， (233) 式を \(z\) で積分し, 河床( \(z=0\) )における濃度を \(c_b\) とすると,

(234)\[c=c_b \exp(-\beta \zeta)\]

なる濃度分布式が得られます．ただし, \(\beta=\cfrac{w_f h}{\epsilon}\) , \(\zeta=z/h\) です. (234) 式は指数分布式，もしくはLane and Kalinske [Ref:12] の式と呼ばれます．この式をもう一度 \(\zeta\) で0から1まで積分すると水深平均濃度 \(<c>\) が求まります．

(235)\[<c>=\displaystyle\int^1_0 c d\zeta= \cfrac{c_b}{\beta}(1-\exp(-\beta))\]

後述の１次元河床変動計算や2次元河床変動計算では浮遊砂濃度は基本的には水深平均値 \(<c>\) として計算されますが，河床変動は河床とコンタクトする底面濃度で扱う必要があるので， 水深平均濃度と河床近傍濃度の関係式が必要になります. (235) 式はこの時に使用されます．