この節の作者: 清水康行 <yasu@i-ric.org>
本テキストへの感想, 質問, 要望, バグ報告などはこちらへお願いします.
差分法の基礎¶
移流方程式の差分解法¶
私たちが扱う時間・空間上の流体問題を記述する微分方程式ので最も基本となる式として, 以下の移流方程式と呼ばれる式があります.
ただし,\(f\) は移流される量,\(x\) は流下方向座標軸,\(t\) は時間, \(c\) は移流速度です. この式は \(f\) という変数が速度 \(c\) でその値を保ちながら \(x\) 方向に輸送されることを表します. (1) 式の理論解はAppendix( 移流方程式の理論解 参照) に示すように比較的簡単に求めることが出来ます.
例えば,(146) の左辺第1項および第2項はこの形式をしており,他にもいろいろな 場面で遭遇する形式の式です. 今, Figure 3 に示すように, \(x\) 軸に沿って \(\Delta x\) 毎に 1, 2, 3, \(\cdots\) , \(i-1, i, i+1\) , \(\cdots\) , \(N-1, N\) , また, \(t\) 軸に沿って, \(\Delta t\) 毎に 1, 2, 3, \(\cdots\) , \(j-1, j, j+1, \cdots, J-1, J\) と分割し,\((x, t)\) における \(f\) を \(f(i,j)\) , \((x+\Delta x, t+\Delta t)\) における \(f\) を \(f(i+1,j+1)\) のように表すこととします.
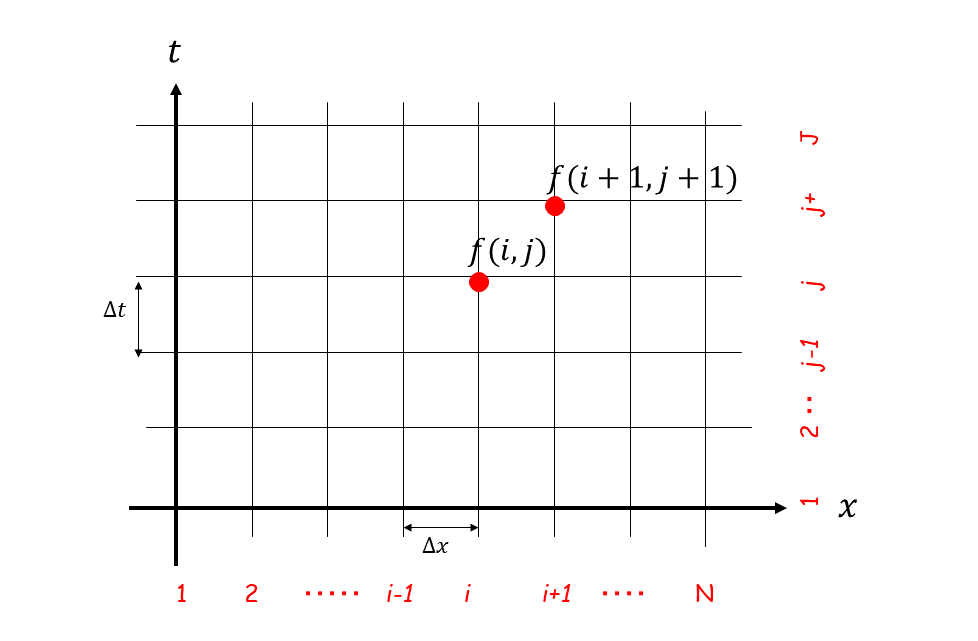
Figure 3 : ( \(x\) , \(t\) ) 空間における離散変数の配置¶
(1) 式の第1項目は時間変化を表していますので,
と表すのが自然です.一方, 第2項については空間微分なので,ごくシンプルな方法として以下の3通りが思いつくでしょう.
上記3つの差分法は,その方向性を考慮して,それぞれ (3) 式が[前進差分], (4) 式が[後進差分], (5) 式が[中央差分]と呼ばれます. 直観的には[中央差分]が最も精度が良いように感じられると思いますが,果たしてどうでしょうか? 次節で実際に確かめてみましょう.
差分法の違いによる解の違い¶
後進差分(Pythonコードと計算結果)¶
前節で挙げた3つの差分法のうちまずは後進差分法でやってみます. (2) 式と (4) 式を (1) 式に代入して整理すると, 次式が得られます.
時間・空間における計算領域を分かりやすく示すために Figure 3 のような \((i,j)\) の 2次元空間を示しましたが,実際には \(j \Rightarrow j+1\) を一旦計算してしまえば, \(j\) における変数はもう不用になるので,この過程をたとえば次のようにコーディングすることにより 1次元問題となります.
for i in range(1,N+1):
fn[i]=f[i]-c*(f[i]-f[i-1])*dt/dx
f=fn
すなわち,一度新しい時間の \(f\) (ここでは fn[i]としてあります)が 算出されたら,それを一旦古い時間の \(f\) と入れ替え, それを用いて次のタイムステップの \(f\) を求め,これを繰り返すという 手続きです.
移流方程式を後進差分法で計算するためのPythonコードを以下に示します.
https://github.com/YasuShimizu/Python-Code/blob/main/backward.py
このコードによる計算結果は下記となります.なお,\(f\) の初期分は Figure 5 に示す三角形分布とし, \(x_p\) =10, \(x_b\) =10, \(f_p\) =0.5, \(c\) =0.5としてあります.
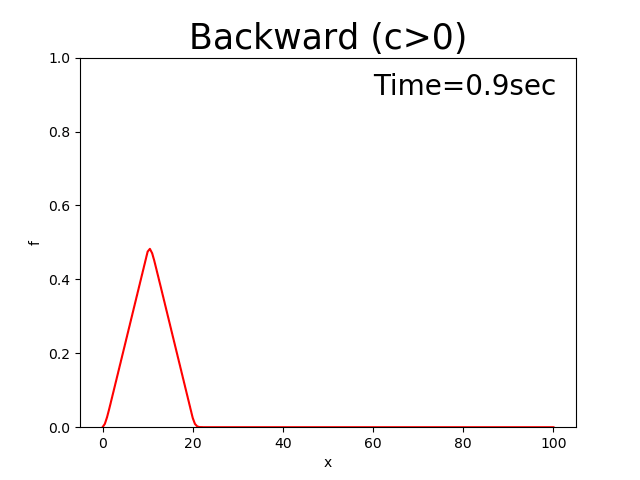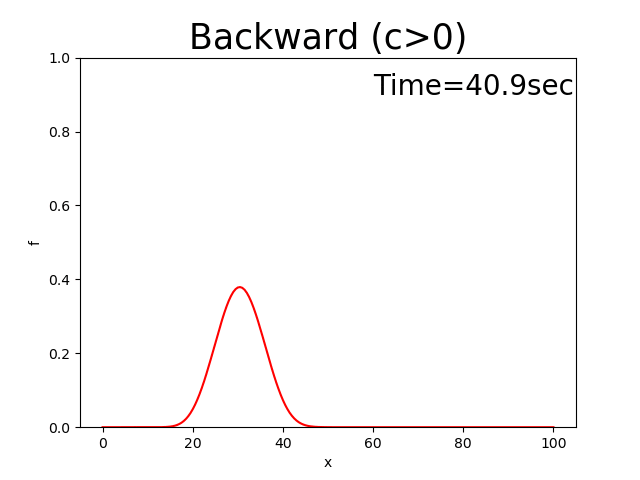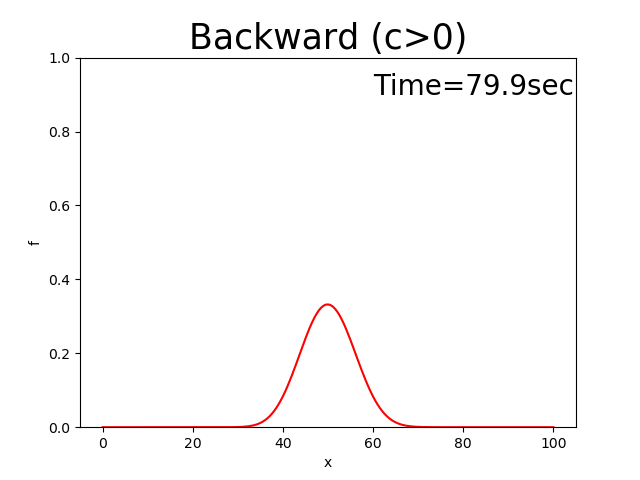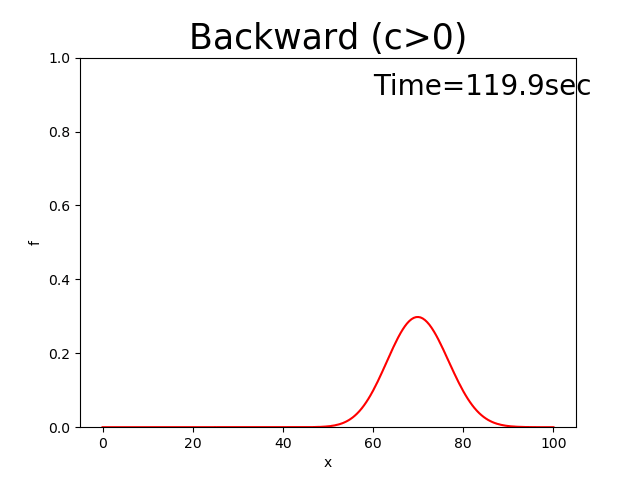
Figure 4 : 後進差分による計算結果( \(c>0\) )¶
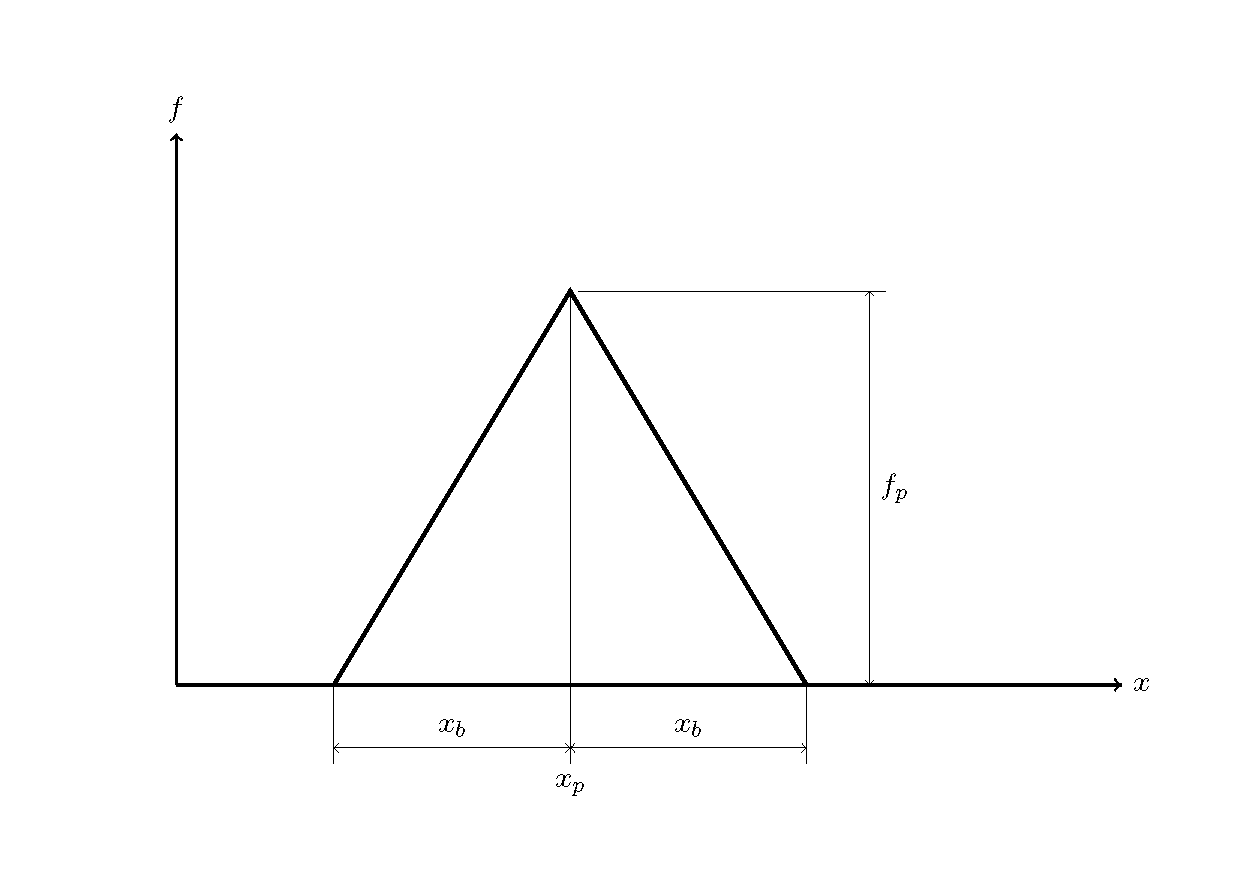
Figure 5 : \(f\) の初期分布¶
Figure 4 を見てすでにお気づきだと思いますが,本来この方程式の解は, Appedixの Figure 142 に示すように, 初期分布である三角形分布が保たれた まま速度 \(c\) で進んで行くべきものが,ピークが徐々に低くなり,三角形の形も 崩れながら進んでいます.この理由は後で説明することにして,次に前進差分と中央差分 でやってみましょう.
前進差分(Pythonコードと計算結果)¶
(2) 式と (3) 式を (1) 式に代入して整理すると, 前進差分を用いた \(f\) の時間更新式として次式が得られます.
この部分のPythonコードは下記のようになります.
for i in range(1,N+1):
fn[i]=f[i]-c*(f[i+1]-f[i])*dt/dx
f=fn
ソースコードはこちらです.
https://github.com/YasuShimizu/Python-Code/blob/main/forward.py
このコードを使って計算した結果は下記のように発散してしまいます('ω')
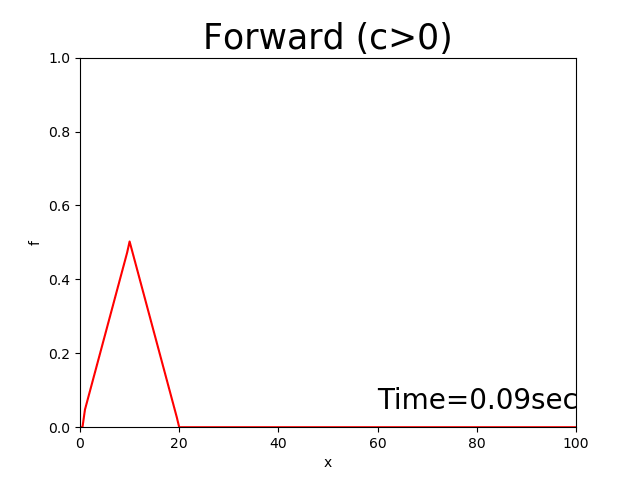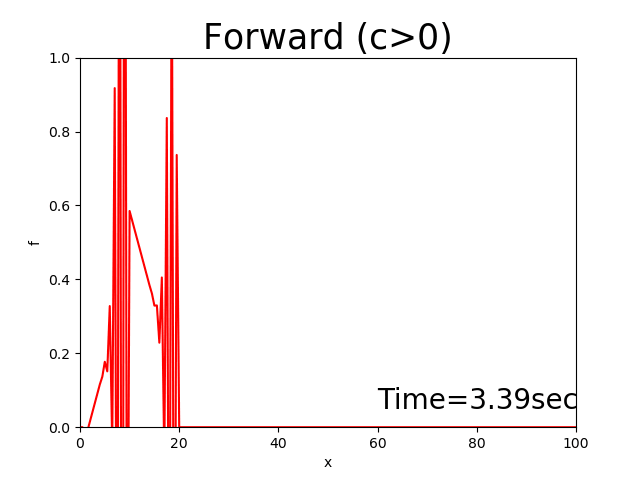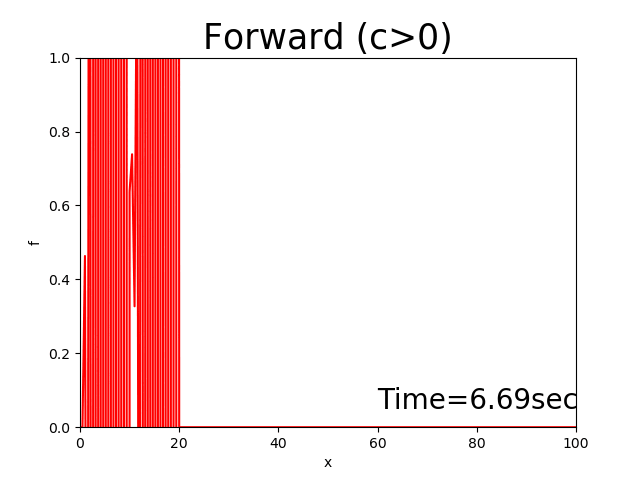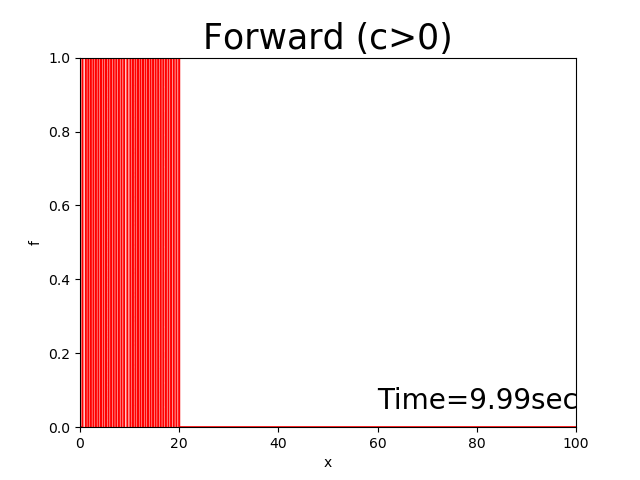
Figure 6 : 前進差分による計算結果( \(c>0\) )¶
中央差分(Pythonコードと計算結果)¶
(2) 式と (5) 式を (1) 式に代入して整理すると, 中央差分を用いた \(f\) の時間更新式として次式が得られます.
これを用いたPythoコードはこちらです.
https://github.com/YasuShimizu/Python-Code/blob/main/central.py
計算結果はこちらです.

Figure 7 : 中央差分による計算結果( \(c>0\) )¶
この場合は,三角形はピークを保って一定速度で移動しているようですが, 後方にノイズが発生し,それがだんだん大きくなって行くようで,最終的には ノイズの最大値が三角形のピーク値を超えるような非現実的な値になっています.
まとめ¶
以上3つの差分法を比較してみましたが,下記の結果となりました.
どの差分法も理論解に一致した結果とはならない.
後進差分は安定した計算結果が得られるが,ピークが減少するなど正確な結果にはならない.
中央差分は初期分布形状の保存性は見られるが,ノイズが多く発生してしまう.
前進差分は計算開始直後に発散してしまう.
移流方向と差分形式¶
ここまでの例はすべて移流速度 \(c\) が正の場合でしたが,次に \(c<0\) の場合も試してみましょう.
Pythonコードと計算結果¶
結果のみ示しますが,以下に \(c<0\) の場合の計算結果および それぞれに対応したPythonコードを示します.
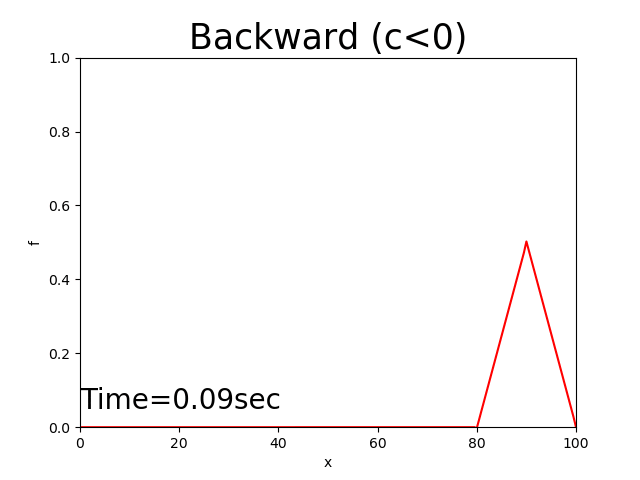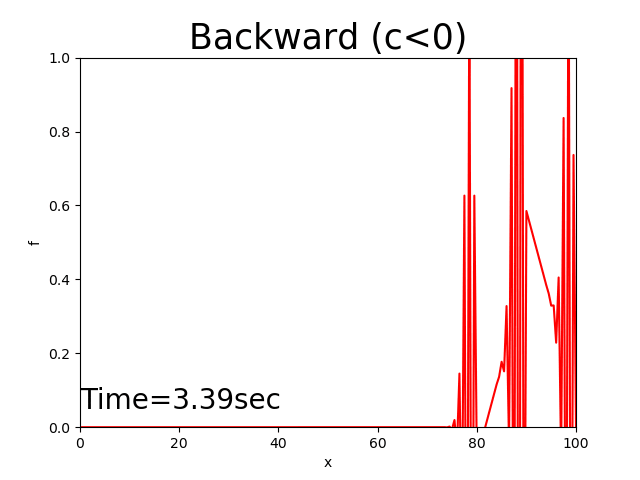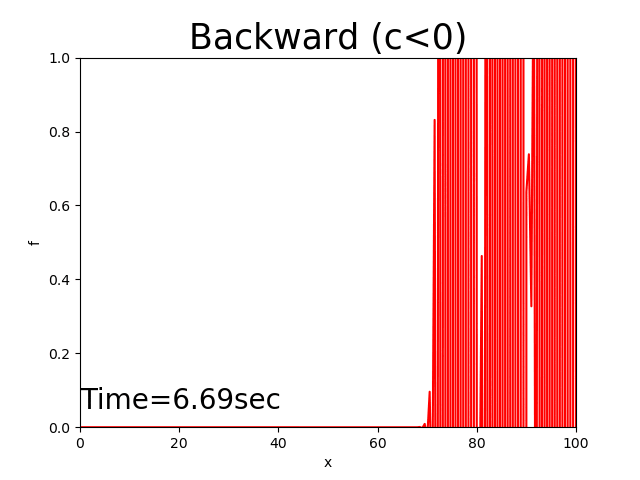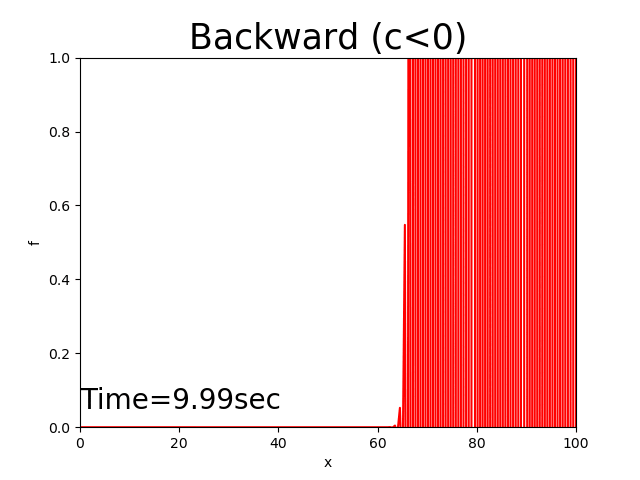
Figure 8 : 後進差分による計算結果( \(c<0\) )¶
https://github.com/YasuShimizu/Python-Code/blob/main/backward-.py
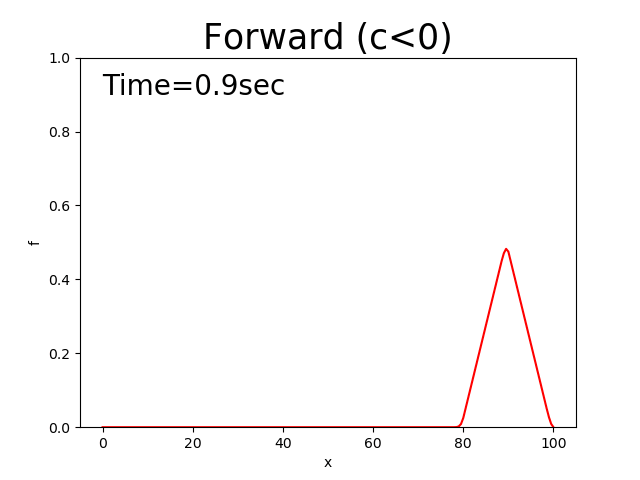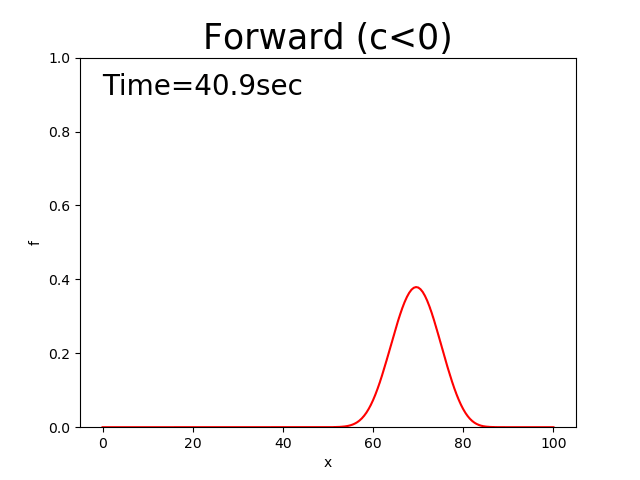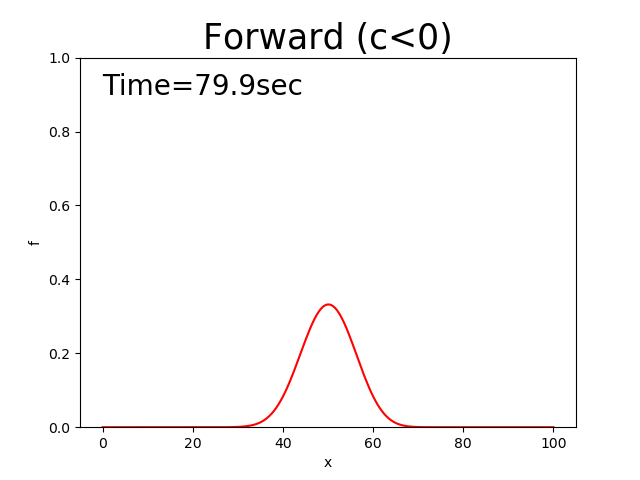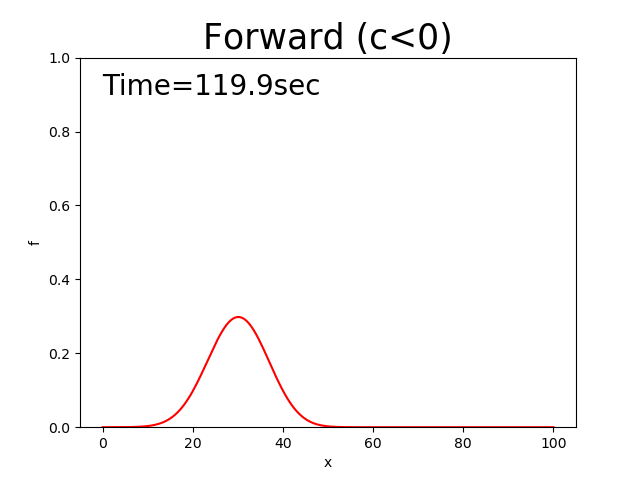
Figure 9 : 前進差分による計算結果( \(c<0\) )¶
https://github.com/YasuShimizu/Python-Code/blob/main/forward-.py

Figure 10 : 中央差分による計算結果( \(c<0\) )¶
https://github.com/YasuShimizu/Python-Code/blob/main/central-.py
以上,\(c>0\) の時と \(c<0\) のときの各差分法の特徴をまとめると下表のように なります.
差分法 |
後進差分( \(i\) と \(i-1\) ) |
前進差分( \(i\) と \(i+1\) ) |
中央差分( \(i-1\) と \(i+1\) ) |
|---|---|---|---|
\(c>0\) のとき |
安定 だが不正確 |
発散 |
やや正確だが不安定 |
\(c<0\) のとき |
発散 |
安定 だが不正確 |
やや正確だが不安定 |
以上,安定して計算が継続出来るのは \(c>0\) の時の後進差分と \(c<0\) の時の前進差分のみです. この2つ, すなわち \(c>0\) ときは i と i-1 を, \(c<0\) のときは i と i+1 位置の情報を使用する差分法のことを \(c\) の方向を風向きに例えて 風上差分法 と呼ばれます. 風上差分という概念は情報が伝わる方向に差分を行うという数値計算上の 非常に重要な概念です.ただし,ここで示したような単純な風上差分法では,計算は安定して進められるが, 計算結果が鈍ってしまうという欠陥があることが分かりました.この欠陥がなぜ生じるかという問題 に対する解答は一旦保留するこにして,次は移流方程式に加えて流体計算上でもう一つの重要な 方程式である拡散方程式の数値解法について解説します.
拡散方程式の差分解法¶
流体計算のもうひとつの重要な基礎パーツに以下の拡散方程式が挙げられます.
ここで, \(D\) は拡散係数です.ここで (9) 式の意味を考えてみましょう.
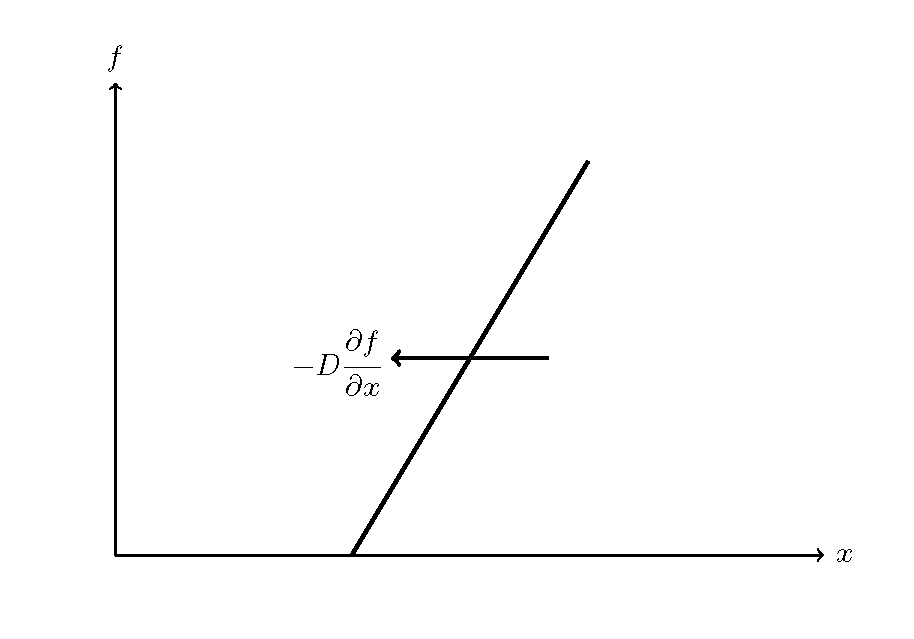
Figure 11 : 拡散方程式の説明(1)¶
今 \(f\) を濃度とし, Figure 11 に示すように \(\cfrac{\partial f}{\partial x}\) なる濃度勾配が生じているとき時に 濃度の高い方から低い方に向かってこの濃度勾配に比例する濃度輸送が生じるとした 場合,そのFluxは比例係数を \(D\) とすると, \(-D\cfrac{\partial f}{\partial x}\) で表されます.ここで勾配が正の時は \(x\) 軸と反対方向にFlux輸送が生じるので,正の輸送量を表すためにマイナスが付いていることに 注意して下さい.
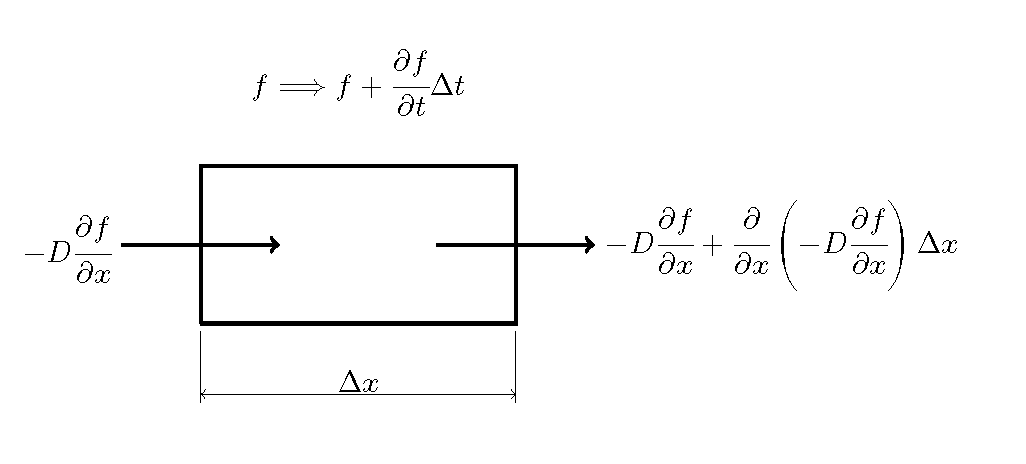
Figure 12 : 拡散方程式の説明(2)¶
Figure 12 に示すように, \(\Delta x\) 離れた2点間の濃度勾配に起因する Fluxの違いが \(\Delta t\) 時間の間に \(f \Longrightarrow f+\cfrac{\partial f}{\partial t}\Delta t\) なる濃度の変化を生じさせると考えますと,
(10) 式の両辺を \(\Delta x\) と \(\Delta t\) で除して, \(D\) を定数とすると (9) 式が得られます. (9) の右辺の2回微分は,計算点の前後(上下流)で一回微分を計算し, それをもう一度微分することにより2回微分が求まります.即ち,
左辺の時間微分項目が単純に時間差を考えると,結局 (9) の差分表示は 次式となります.
または
これを,前節の移流方程式でやったように,f とfnで逐次入れ替えながら計算する方式で コーディングすると,下記のようになります.
for i in range(1,N+1):
fn[i]=f[i]+D*(f[i+1]-2*f[i]+f[i-1])*dt/dx**2
f=fn
Pythonコードと計算結果¶
ソースコード全体はこちらです.また,\(D=0.8\) とした計算結果を Figure 13 に示します.
https://github.com/YasuShimizu/Python-Code/blob/main/diffusion.py

Figure 13 : 拡散方程式の計算結果¶
Figure 13 はピークが潰れながら広がっていく 文字通りの拡散現象を表しており,妥当なものであることが分かります.
ところで気がついたと思いますが,風上差分に相当する Figure 4 や Figure 9 にも,同じような 拡散現象が見られます.もともと移流方程式の解はこのように拡散せずに 初期の分布形状を保ったまま移動するはずなのに( Figure 142 ) 何故か移流と同時に拡散が生じています.このように,移流方程式の解には本来含まれ無いはずの 「拡散」が数値計算によって現れてしまうことが知られており,これは,本来の「拡散」と区別して 「数値拡散」と呼ばれます. では,何故この「数値拡散」が生じてしまうのかを考えてみましょう.
風上差分と数値拡散¶
風上差分では,移流の方向すなわち \(c\) の符号によって差分の方向を 変える必要があります.コーディングにおいてはその都度if文で判断すれば 良いのですが,その特性を説明する場合はif文を使わないほうが分かりやすので, ここではif文を使わないで風上差分を表現する方法を示します. まずは,以下のような式を考えます.
したがって,
(15) 式の特徴を考慮して以下のような数式を考えてみます.
したがって,
または,
は1つの式でif文を使わないで風上差分を表す式となっています. ただし \(f_n(i)\) および \(f(i)\) はそれぞれ, \(f(i,j+1)=f(x,t+\Delta y)\) および \(f(i,j)=f(x,t)\) を表している.
(19) 式より風上差分は次式で表すことが出来ます.
ここで,(8) 式の移流方程式の中央差分と, (13) 式の拡散方程式の差分式 も同じ方式で再記してみると,
移流方程式の中央差分は,
拡散方程式は,
ですが, \(D=\cfrac{|c|\Delta x}{2}\) とすると,
となります.これらの式を見ると,(20) 式の a と, (21) 式の a', また, (20) 式の b と, (23) 式の b' 部分が一致していることが 分かります. これは, (20) 式が表す移流方程式の風上差分法の ( a+b )の部分は, 実は中央差分( a' )と拡散方程式( b' )の2つに分けられ,これらを足し合わせた 形式になっているということを意味しています.この b の部分の拡散はもともとは移流方程式ですから, 含まれていないにも関わらず,風上差分を行うと自動的に入ってしまう要素です.これを本来の物理的な意味の 「拡散」に対して,数値計算を行うと入ってきてしまうということで「数値拡散」と呼ばれます. これが,「数値拡散」の正体です.
風上差分に相当するのは Figure 4 と Figure 9 ですが,確かに形を保ちながら一定 スピードで移動する中央差分の特性と,ピークを低下させながら裾野を広げていく拡散の特性が合成された 結果となっています.
ただし,この風上差分は確かに安定した計算結果が得られますがけっして正確な値ではありません. 目指すのはあくまでも Figure 142 に示すような理論解に出来るだけ近い数値計算結果です. ということで次章では出来るだけ数値拡散の少ない差分法について述べます.