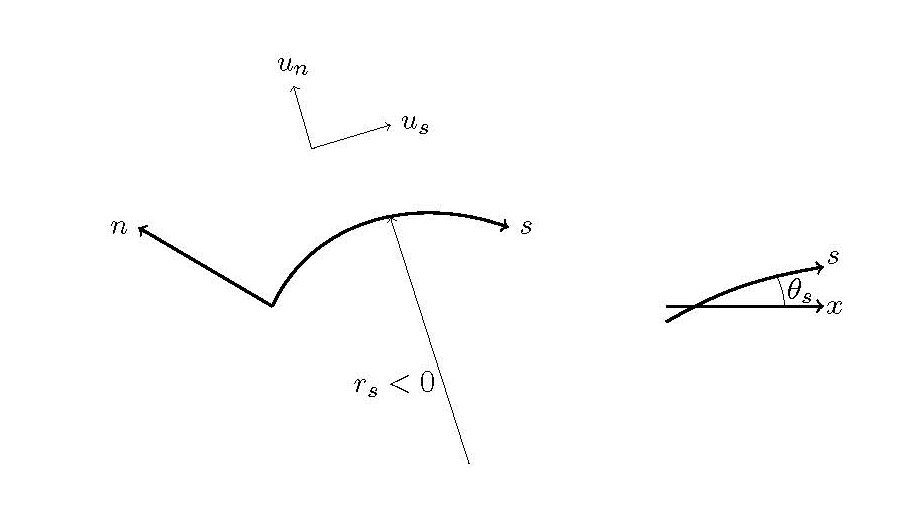主流の鉛直方向流速分布
水深平均流の流れ方向を \(s\) ,鉛直上向き方向を \(z\) とすると,
\(s\) 方向の等流流れの運動方程式は次式で表されます.
(453)\[0=-g{{\partial H}\over{\partial s}}+{\partial \over{\partial z}} \left(\nu_t{{\partial u_s}\over{\partial z}}\right)\]
ここで,\(g\) は重力加速度,\(H\) は水位,\(s\) は主流の流下方向, \(u_s\)
は \(s\) 方向の流速,\(z\) は鉛直方向座標軸, \(\nu_t\) は渦動粘性係数です.
鉛直方向距離を水深 \(h\) で無次元化し,河床高を \(z_b\) ,無次元鉛直方向距離を
\(\zeta\) (河床で0, 水面で1)とし,次式で表します.
(454)\[\zeta=\cfrac{z-z_b}{h}\]
等流状態を仮定し,エネルギー勾配(=水面勾配)を \(I_e\) とすると, \(I_e\) は次式で
表されます.
(455)\[I_e=-{{\partial H}\over{\partial s}}\]
主流の水深平均流速を \(<u_s>\) とし, 次式で表します.
(456)\[u_s(\zeta)=<u_s>f_s(\zeta)\]
ただし, f_s は
これを運動方程式 (453) に代入します.
(457)\[\cfrac{\partial^2 f_s}{\partial \zeta^2}=-\cfrac{gI_eh^2}{\nu_t <u_s>}\]
\(\zeta\) で積分すると,
(458)\[{{\partial f_s}\over{\partial \zeta}}=-\cfrac{gI_eh^2}{\nu_t<u_s>}\zeta+C_1\]
となります. ただし, \(C_1\) は積分定数です. 水面でせん断力がゼロなので,\(\zeta=1\) で
\(\cfrac{\partial f_s}{\partial \zeta}=0\) より \(C_1\) は次式となり,
これを \(\beta\) と置くと,
(459)\[C_1=\cfrac{gI_eh^2}{\nu_t<u_s>} \equiv \beta\]
となり, (458) 式は次式となります.
(460)\[{{\partial f_s}\over{\partial \zeta}}=\beta(1-\zeta)\]
これをもう一度 \(\zeta\) で積分すると, \(C_2\) を積分定数として
\(f_s\) は
(461)\[f_s=\beta\left(\zeta-\cfrac{1}{2}\zeta^2\right)+C_2\]
となり, 平均流の定義より,
(462)\[\int_0^1 f_s d\zeta =1=
\left[
\beta\left(\cfrac{1}{2}\zeta^2-\cfrac{1}{6}\zeta^3\right)+C_2\zeta
\right]^1_0
=\cfrac{1}{3}\beta+C_2\]
なので,
(463)\[C_2=1-\cfrac{1}{3}\beta\]
となります. これを (462) 式に戻すと次式が得られます.
(464)\[f_s=\left(-{1 \over 2}\zeta^2+\zeta-{1 \over 3}\right)\beta+1\]
渦動粘性係数を \(\nu_t=\alpha u_\ast h\) で表し,
摩擦速度 \(u_\ast\) が, \(u_\ast=\sqrt
{ghI_e}\) であることを考慮すると,
(465)\[\beta=\cfrac{gI_eh^2}{\nu_t<u_s>}=\cfrac{gI_eh}{\alpha u_\ast <u_s>}=\cfrac{u_\ast}{\alpha<u_s>}\]
となり, 底面での流速(Slip Velocity)を \(u_s^b\) とすると
(466)\[u_s^b=<u_s>f_s(0)=-\cfrac{u_\ast}{3\alpha}+<u_s>\]
より,
(467)\[\cfrac{<u_s>}{u_\ast} = \cfrac{u_s^b}{u_\ast}+\cfrac{1}{3\alpha}\]
(468)\[\cfrac{u_s^b}{u_\ast}=2+{{1}\over{\kappa}} \ln {{h}\over{k_s}} =r_\ast\]
とおくと,
(469)\[u_\ast^2h(1-\xi)=\alpha u_* h{{\partial u}\over{\partial \xi}}\]
したがって,
(470)\[\cfrac{<u_s>}{u_\ast} = r_\ast+\cfrac{1}{3\alpha}\]
(471)\[\cfrac{u_\ast}{<u_s>}= \cfrac{1}{r_\ast + \cfrac{1}{3\alpha}}
=\cfrac{3\alpha}{3\alpha r_\ast +1}\]
これを (464) 式に代入すると
(472)\[\beta=\left(\cfrac{3\alpha}{3\alpha r_\ast +1}\right)\cfrac{1}{\alpha}
=\cfrac{1}{\alpha r_\ast+\cfrac{1}{3}}\]
(473)\[\cfrac{1}{\beta} = \alpha r_\ast + \cfrac{1}{3}\]
ゆえに,
(474)\[f_s=\left(
-\cfrac{1}{2}\zeta^2+\zeta-\cfrac{1}{3}\right)\beta+1
=\left(
-\cfrac{1}{2}\zeta^2+\zeta-\cfrac{1}{3}+\cfrac{1}{\beta}
\right)\beta
=\cfrac{\alpha r_\ast + \zeta - \cfrac{1}{2} \zeta^2}{\alpha r_\ast + \cfrac{1}{3}}\]
ここで, \(r_\ast \alpha=\chi\) , \(\chi_1=\alpha r_\ast +\cfrac{1}{3}\) とすると,
(475)\[f_s=\cfrac{\chi+\zeta-\cfrac{\zeta^2}{2}}{\chi_1}\]
したがって, \(u_s(\zeta)\) は次式となります.
(476)\[u_s(\zeta)=<u_s>\cfrac{\chi+\zeta-\cfrac{\zeta^2}{2}}{\chi_1}\]
(476) 式が 放物線分布 と呼ばれる流線方向の流速鉛直分布式です.
2次流の流速分布
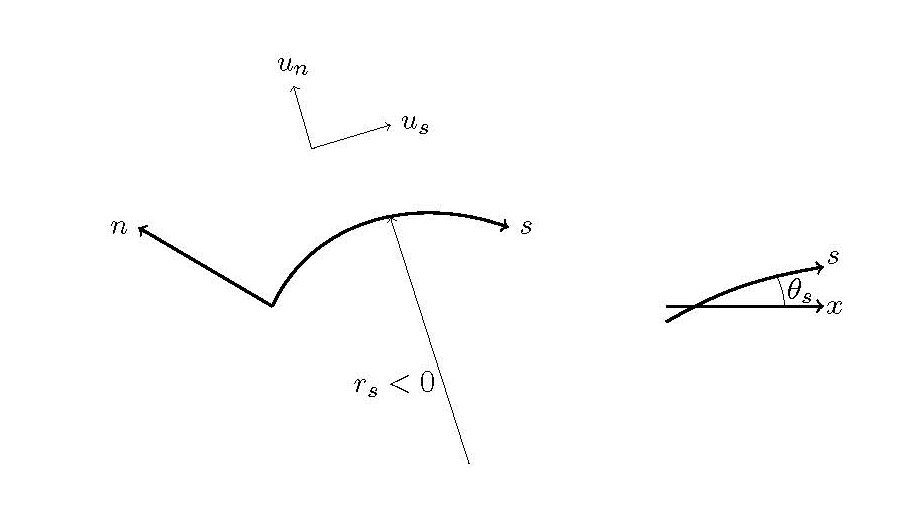
Figure 156 : 座標系の定義
Figure 156 に示すように,
主流方向の流れが曲率半径 \(r_s\) でカーブしている場合(主流方向を \(s\) 軸とし,
\(s\) 軸に向かって右にカーブしている場合を \(r_s>0\) とする, Figure 156 では \(r_s<0\) となる),
\(n\) 軸を \(s\) 軸に直交する方向で \(s\) が増加する方向に向かって左側が正になる方向に取り,\(n\) 方向の流速を \(u_n\) とすると,\(n\) 軸方向の等流流れの運動方程式は次式で表されます.
(477)\[{{u_s^2}\over{r_s}} = -g{{\partial H}\over{\partial n}} +{{\partial}\over{\partial z}}
\left( \nu_t {{\partial u_n}\over{\partial z}} \right)\]
ただし,
(478)\[\cfrac{1}{r_s}= \cfrac{\partial \theta_s}{\partial s}\]
ここで,\(\theta\) は \(x\) 軸と主流方向 \(s\) とのなす角度です.
\(n\) 方向の流速に以下の分布を仮定します.
(479)\[u_n(\zeta)=A_n f_n(\zeta)\]
ただし, \(A_n\) は2次流強度を表す係数,\(f_n\) は無次元流速分布関数です.
これを (477) に代入して整理すると,
(480)\[\cfrac{\partial^2 f_n}{\partial \zeta^2}=\cfrac{g h^2}{\nu_t A_n} \cfrac{\partial H}{\partial n}
+\cfrac{<u_s>^2 h^2}{\nu_t A_n r_s} f_s^2
=\cfrac{<u_s>^2h^2}{\nu_t A_n r_s} \left( \cfrac{g r_s}{<u_s>^2}\cfrac{\partial H}{\partial n}
+f_s^2 \right)\]
ここで,
(481)\[\cfrac{<u_s>^2h^2}{\nu_t A_n r_s} \equiv A\]
(482)\[\cfrac{g r_s}{<u_s>^2}\cfrac{\partial H}{\partial n} \equiv B\]
とおくと, (480) 式は,
(483)\[\cfrac{\partial^2 f_n}{\partial \zeta^2}=A(B+f_s^2)\]
と書けます,これを, \(\zeta\) で積分しますと,
(484)\[\begin{split}\cfrac{\partial f_n}{\partial \zeta}
=AB\zeta+ A\int \left[\left\{{ {1}\over{\chi_1}}
\left( \chi + \zeta -{{1}\over{2}} \zeta^2 \right)\right\}^2
\right] d\zeta + C_3 \\
=AB \zeta + \cfrac{A}{{\chi_1}^2} \left[
\chi^2 \zeta + \chi \zeta^2 +{{1}\over{3}}(1-\chi)\zeta^3-{{1}\over{4}}\zeta^4+
{{1}\over{20}}\zeta^5 \right] +C_3\end{split}\]
となる.ただし \(C_3\) は積分定数です.
水面では \(\cfrac{\partial f_n}{\partial \zeta}=0\) (Slip条件)なので,
(485)\[C_3=-AB - \cfrac{A}{{\chi_1}^2} \left(\chi^2+{{2}\over{3}}\chi+{{2}\over{15}} \right)\]
よって,
(486)\[\begin{split}\cfrac{\partial f_n}{\partial \zeta}
=AB \zeta + \cfrac{A}{{\chi_1}^2} \left[
\chi^2 \zeta + \chi \zeta^2 +{{1}\over{3}}(1-\chi)\zeta^3-{{1}\over{4}}\zeta^4+
{{1}\over{20}}\zeta^5 \right] \\
-\left[
AB + \cfrac{A}{{\chi_1}^2} \left(\chi^2+{{2}\over{3}}\chi+{{2}\over{15}} \right)
\right]\end{split}\]
これをもう1度 \(\zeta\) に関して積分します.
(487)\[\begin{split}f_n={{1}\over{2}} AB\zeta^2 +\cfrac{A}{{\chi_1}^2} \left[
{{1}\over{2}}\chi^2 \zeta^2 + {{1}\over{3}}\chi \zeta^3 +{{1}\over{12}}(1-\chi)\zeta^4-{{1}\over{20}}\zeta^5+
{{1}\over{120}}\zeta^6 \right] \\
-\left[
AB + \cfrac{A}{{\chi_1}^2} \left(\chi^2+{{2}\over{3}}\chi+{{2}\over{15}} \right)
\right]\zeta + C_4\end{split}\]
ただし, \(C_4\) は積分定数です. 2次流はその定義から水深方向積分値はゼロになります.
すなわち \(\displaystyle{\int_0^1 f_n d\zeta =0}\) なので,
(488)\[\begin{split}\int_0^1 f_n d \zeta =
{{1}\over{6}} AB\zeta^3 +\cfrac{A}{{\chi_1}^2} \left[
{{1}\over{6}}\chi^2 \zeta^3 + {{1}\over{12}}\chi \zeta^4 +{{1}\over{60}}(1-\chi)\zeta^5-{{1}\over{120}}\zeta^6+
{{1}\over{840}}\zeta^7 \right] \\
-\left[
AB + \cfrac{A}{{\chi_1}^2} \left(\chi^2+{{2}\over{3}}\chi+{{2}\over{15}} \right)
\right]\cfrac{\zeta^2}{2} + C_4\zeta =0\end{split}\]
これより,
(489)\[C_4={{1}\over{3}}AB + \cfrac{A}{{\chi_1}^2} \left[
{{1}\over{3}} \chi^2 +{{4}\over{15}}\chi +{{2}\over{35}} \right]\]
これを (487) 式に代入しますと,
(490)\[\begin{split}f_n={{A}\over{2}} \left(B+\cfrac{\chi^2}{{\chi_1}^2}\right)\zeta^2 +\cfrac{A}{{\chi_1}^2} \left[
{{1}\over{3}}\chi \zeta^3 +{{1}\over{12}}(1-\chi)\zeta^4-{{1}\over{20}}\zeta^5+
{{1}\over{120}}\zeta^6 \right] \\
-\left[
AB + \cfrac{A}{{\chi_1}^2} \left(\chi^2+{{2}\over{3}}\chi+{{2}\over{15}} \right)
\right]\zeta +{{1}\over{3}}AB+\cfrac{A}{{\chi_1}^2}
\left({{1}\over{3}}\chi^2+{{4}\over{15}}\chi+{{2}\over{35}}\right)\end{split}\]
一方, 底面流速ベクトルの方向とせん断力ベクトルの方向は同ですので,
(491)\[\cfrac{u_n^b}{u_s^b} = \cfrac{\tau_n^b}{\tau_s^b}\]
ただし, \(u_s^b, u_n^b, \tau_s^b, \tau_n^b\) はそれぞれ,
\(s\) 方向よよび, \(n\) 方向の底面流速および河床せん断力です.
(491) 式中の各値は下記 (492) \(\sim\) (495) です.
(492)\[u_s^b=<u_s>f_s(0)=<u_s> \cfrac{\chi}{\chi_1}\]
(493)\[u_n^b=A_n f_n(0) = A A_n \left[{{1}\over{3}}B + {{1}\over{{\chi_1}^2}} \left(
{{1}\over{3}}\chi^2+{{4}\over{15}}\chi+{{2}\over{35}} \right) \right]\]
(494)\[\cfrac{\tau_s^b}{\rho} = u_\ast^2\]
(495)\[\cfrac{\tau_n^b}{\rho} = \nu_t \left. \cfrac{\partial u_n}{\partial z} \right|_{z=0}
=\nu_t \cfrac{A_n}{h} \left. \cfrac{\partial f_n}{\partial \zeta} \right|_{\zeta=0}
=-\alpha u_\ast A_n A \left[
B+{{1}\over{{\chi_1}^2}} \left(\chi^2+{{2}\over{3}}\chi +{{2}\over{15}} \right) \right]\]
これらを (491) 式に代入します.
(496)\[\begin{split}\cfrac{ A A_n \left[\cfrac{1}{3}B + \cfrac{1}{{\chi_1}^2} \left(
\cfrac{1}{3}\chi^2+\cfrac{4}{15}\chi+\cfrac{2}{35} \right) \right]}
{<u_s> \cfrac{\chi}{\chi_1}} \\
=-\cfrac{\alpha u_\ast A_n A \left[
B+\cfrac{1}{{\chi_1}^2} \left(\chi^2+\cfrac{2}{3}\chi +\cfrac{2}{15} \right) \right]}
{u_\ast^2} \\
\cfrac{1}{3}B+\cfrac{1}{{\chi_1}^2} \left(
\cfrac{1}{3}\chi^2+\cfrac{4}{15}\chi+\cfrac{2}{35} \right) \\
=-\alpha \cfrac{<u_s>}{u_\ast} \cfrac{\chi}{\chi_1}
\left[
B+\cfrac{1}{{\chi_1}^2} \left(\chi^2+\cfrac{2}{3}\chi +\cfrac{2}{15} \right) \right]\end{split}\]
ここで,
(497)\[\cfrac{<u_s>}{u_\ast} =
r_\ast +\cfrac{1}{3\alpha}=\cfrac{\chi_1}{\alpha}, \; \;
\chi_1=\chi+\cfrac{1}{3}\]
の関係を用いると,
(498)\[\cfrac{1}{3}B+\cfrac{1}{{\chi_1}^2} \left(
\cfrac{1}{3}\chi^2+\cfrac{4}{15}\chi+\cfrac{2}{35} \right)
=-\chi \left[
B+\cfrac{1}{{\chi_1}^2} \left(\chi^2+\cfrac{2}{3}\chi +\cfrac{2}{15} \right) \right]\]
(499)\[\left(\chi+\cfrac{1}{3}\right)B=-\cfrac{1}{{\chi_1}^2}
\left(\chi^3+\chi^2+\cfrac{2}{5}\chi+\cfrac{2}{35}\right)\]
(500)\[B=-\cfrac{1}{{\chi_1}^3}\left(\chi^3+\chi^2+\cfrac{2}{5}\chi+\cfrac{2}{35}\right)\]
となります. これより \(f_n\) は
(501)\[\begin{split}\cfrac{f_n}{A}=\cfrac{1}{2}\left(B+\cfrac{\chi^2}{{\chi_1}^2}\right)\zeta^2
+\cfrac{1}{{\chi_1}^2} \left[
\cfrac{1}{3}\chi\zeta^3+\cfrac{1}{12}(1-\chi)\zeta^4-\cfrac{1}{20}\zeta^5+\cfrac{1}{120}\zeta^6 \right] \\
-\left[B+\cfrac{1}{{\chi_1}^2}\left(\chi^2+\cfrac{2}{3}\chi+\cfrac{2}{15}\right)\right]\zeta
+\left[\cfrac{1}{3}B+\cfrac{1}{{\chi_1}^2}\left(\cfrac{1}{3}\chi^2+\cfrac{4}{15}\chi+\cfrac{2}{35}\right)\right]\end{split}\]
となります. ここで, 右辺最終項は (498) 式の関係を用いると,
(502)\[\begin{split}\cfrac{f_n}{A}=\cfrac{1}{2}\left(B+\cfrac{\chi^2}{{\chi_1}^2}\right)\zeta^2
+\cfrac{1}{{\chi_1}^2} \left[
\cfrac{1}{3}\chi\zeta^3+\cfrac{1}{12}(1-\chi)\zeta^4-\cfrac{1}{20}\zeta^5+\cfrac{1}{120}\zeta^6 \right] \\
-\left[B+\cfrac{1}{{\chi_1}^2}\left(\chi^2+\cfrac{2}{3}\chi+\cfrac{2}{15}\right)\right]\zeta
-\chi \left[
B+\cfrac{1}{{\chi_1}^2} \left(\chi^2+\cfrac{2}{3}\chi +\cfrac{2}{15} \right) \right] \\
=\cfrac{1}{{\chi_1}^2} \left[
-\left(\chi^2+\cfrac{2}{3}\chi+\cfrac{2}{15}\right) \left(\zeta+\chi\right)
+\cfrac{1}{2}\chi^2 \zeta^2+\cfrac{1}{3}\chi\zeta^3 \right. \\
+\left. \cfrac{1}{12}\left(1-\chi \right)\zeta^4-\cfrac{1}{20}\zeta^5+\cfrac{1}{120}\zeta^6
\right]+B\left(\cfrac{1}{2}\zeta^2-\zeta-\chi\right)\end{split}\]
となります. ここで,
(503)\[\begin{split}A=\cfrac{<u_s>^2 h^2}{\nu_t A_n r_s}=
\cfrac{1}{A_n} \cfrac{<u_s>^2 h^2}{\alpha u_\ast h r_s} \\
=\cfrac{1}{A_n} \cfrac{1}{\alpha} \cfrac{<u_s>}{u_\ast} <u_s> \cfrac{h}{r_s}
=\cfrac{1}{A_n} \cfrac{1}{C_f \chi_1} <u_s> \cfrac{h}{r_s}\end{split}\]
なので,2次流強度 \(A_n\) を
(504)\[A_n = <u_s>\cfrac{h}{r_s}\]
と定義すると,最終的に2次流分布は下記のようになります.
(505)\[u_n=A_n f_n, \; \; f_n=\cfrac{G_0(\zeta)}{C_f \chi_1}\]
ただし,
(506)\[\begin{split}G_0(\zeta)=\cfrac{1}{{\chi_1}^2}\left[
-\left(\chi^2+\cfrac{2}{3}\chi+\cfrac{2}{15}\right)\left(\zeta+\chi\right)+\cfrac{1}{2}\chi^2\zeta^2+\cfrac{1}{3}\chi\zeta^3 \right. \\
\left. +\cfrac{1}{12}\left(1-\chi\right)\zeta^4 -\cfrac{1}{20}\zeta^5+\cfrac{1}{120}\zeta^6 \right]+\chi_{20}\left(\cfrac{1}{2}\zeta^2-\zeta-\chi\right)\end{split}\]
(507)\[\chi_{20} = B = -\cfrac{1}{{\chi_1}^3} \left(\chi^3+\chi^2+\cfrac{2}{5}\chi+\cfrac{2}{35}\right), \: \: \cfrac{<u_s>}{u_\ast} = \cfrac{1}{\sqrt{C_f}}, \; \chi=\chi_1-\cfrac{1}{3}\]
これがEngelundによる2次流の6次式です.
底面流速
河床変動計算においては2次流の影響を考慮した底面流速の方向(流砂の方向)が重要になります.
ここまで得られた流速分布から底面流速を求めます.
(508)\[\begin{split}\left. u_n\right|_{z=0}=A_n f_n(0) \\
=\cfrac{A_n}{C_f \chi_1} \left[
-\cfrac{\chi}{{\chi_1}^2}\left(\chi^2+\cfrac{2}{3}\chi+\cfrac{2}{15}\right)
+\cfrac{\chi}{{\chi_1}^3} \left(\chi^3+\chi^2+\cfrac{2}{5}\chi+\cfrac{2}{35}\right) \right] \\
=\cfrac{A_n \chi}{C_f {\chi_1}^4} \left[
\left(\chi^3+\chi^2+\cfrac{2}{5}\chi+\cfrac{2}{35}\right)
-\chi_1 \left(\chi^2+\cfrac{2}{3}\chi+\cfrac{2}{15}\right) \right] \\
=\cfrac{A_n \chi}{C_f {\chi_1}^4} \left[
\left(\chi^3+\chi^2+\cfrac{2}{5}\chi+\cfrac{2}{35}\right)
-\left( \chi + {1 \over 3} \right)\left(\chi^2+\cfrac{2}{3}\chi+\cfrac{2}{15}\right) \right] \\
=\cfrac{A_n \chi}{C_f {\chi_1}^4} \left(\cfrac{2}{45}\chi+\cfrac{4}{315}\right)\end{split}\]
なお, 一般的に良く2次元モデルで使用される横断方向( \(n\) 方向)の底面流速式は
(509)\[\left. u_n \right|_{z=0} = \left. u_s \right|_{z=0} N_\ast \cfrac{h}{r_s}\]
のような形で主流方向( \(s\) 方向)の底面との関係で示される場合が多い.
主流の底面流速は,
ですので,
(510)\[\left. u_n \right|_{z=0} = \cfrac{\chi}{\chi_1} N_\ast <u_s> \cfrac{h}{r_s}\]
となります. 一方, (508) 式で平衡状態の \(A_n\) を与えれば,
(511)\[\left. u_n \right|_{z=0}
=\cfrac{A_n \chi}{C_f {\chi_1}^4} \left(\cfrac{2}{45}\chi+\cfrac{4}{315}\right)
=\cfrac{\chi}{C_f {\chi_1}^4} \left(\cfrac{2}{45}\chi+\cfrac{4}{315}\right)
<u_s>\cfrac{h}{r_s}\]
ここで, (510) 式と (511) 式を比較すると,
(512)\[N_\ast =\cfrac{1}{C_f {\chi_1}^3} \left(\cfrac{2}{45}\chi + \cfrac{4}{315}\right)\]
と表すことが出来ます.
2次流強度について
例えば, \(\alpha=\cfrac{\kappa}{6}=0.077\) , \(C_f=0.01\) とすれば,
\(N_\ast=7.03\) となりこれが, 2次元河床変動計算で良く使用される 2次流強度 \(N_\ast=7\) の根拠 ということに
なります.
逆に \(N_\ast\) を条件として与えた場合,
(513)\[C_f =\cfrac{1}{N_\ast {\chi_1}^3} \left(\cfrac{2}{45}\chi + \cfrac{4}{315}\right)\]
となります.