この節の作者: 清水康行 <yasu@i-ric.org>

本テキストへの感想, 質問, 要望, バグ報告などはこちらへお願いします.

蛇行河川の河床変動計算(基礎編)

2次流と底面せん断力の方向について

2次流とは

平面2次元計算において河床変動計算を行う場合, 水深平均流の計算で得られる流速ベクトルの他に， 2次流を考慮した河床底面近傍の流速ベクトルが重要になります．これは河床変動計算においては 流砂の方向が重要となり, 流砂の方向は底面近傍流速の方向により決定されるためです. 通常, 平面上での流れが曲がることにより遠心力が生じ， これにより流線方向に軸を持つ螺旋状の2次流と呼ばれる副次的な流れが発生します． なお, 2次流に対してもともとの流下方向に向かう流れを主流と言います．

注釈

前章までの記述では流れ場は水深平均流れ場を扱ってきましたので，流速として例えば \(u_s\) は \(s\) 軸方向の水深平均流速を表していました． しかしながらこれから扱う2次流などの解説 では流速は深さ方向にも分布を待つ扱いなので，\(u_s\) なども水深平均ではなく， 深さ方向に分布を持った値として扱われます．なお，水深平均流速については，深さ方向に分布を持った 値の水深平均値という意味で \(<\;>\) で囲って, \(<u_s>\) という形で表すことにします． 表現が紛らわしくなりましが，注意して読んで下さい．

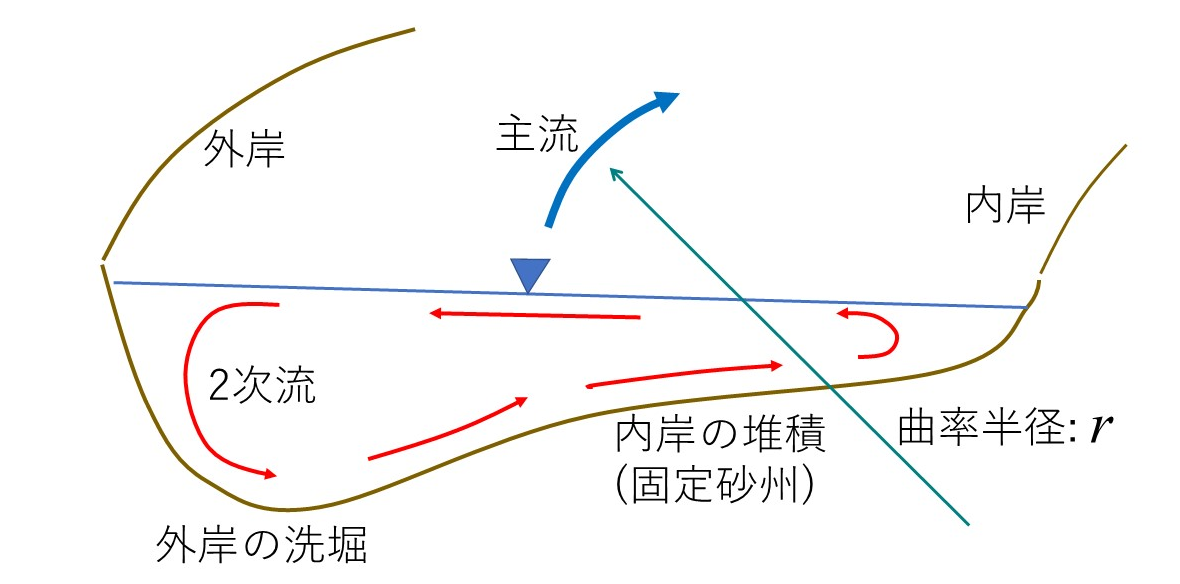
Figure 118 : 2次流

例えば，Figure 118 に示すように流路が湾曲している場合, 主流は流路に沿って曲がるため, 次式で表される遠心力が生じます．

(276)\[F_s = \cfrac{u_s^2}{r}\]

ただし, \(F_s\) は遠心力, \(u_s\) は主流方向の流速, \(r\) は主流の曲がりの曲率半径 です. 主流の鉛直方向流速分布は良く知られている対数則や放物線分布などのように, 抵抗の無い水面では速く, 底面の影響を受ける河床近傍では遅くなるため (276) 式のように 流速の2乗に比例する遠心力は水面付近で圧倒的に大きくなるため，2次流れは水面では外岸に向い, これを 補償する(連続式を満たすための)内岸に向かう流れが底面で生じ，この結果横断面全体を 循環するような2次流が発生します．移動床流路の外岸側は洗堀し，内岸側は堆積し砂州が形成されるのは， 主としてこの2次流に起因するものです．

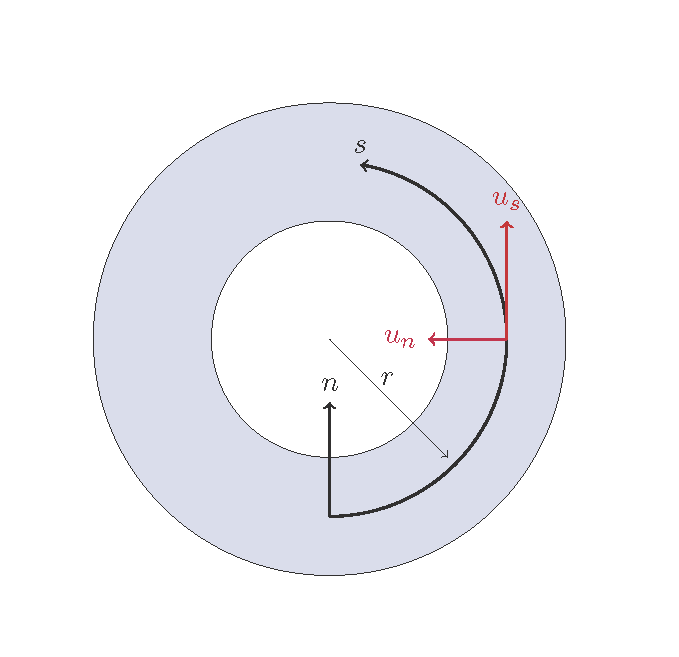
Figure 119 : 同心円水路における一様湾曲流

2次流の特性を考える場合，最も単純化された状態として, Figure 119 に示すような一様湾曲流を想定する ことにより解析的な取り扱いが容易になります．この状態は左右岸が同心円上で勾配が一定(勾配があるので実際には同心円が螺旋状に無限に続くような仮想の状況)の水路を想定してます． この仮想水路において流量一定の等流を想定しますので，水深平均流の流線もすべて同心円となるため \(<u_s>\) は等流流速, \(<u_n>=0\) となることが明らかです．

このような一様湾曲流(曲率半径が一定の等流)における2次流お流速分布については古くから多くの研究者により 提案されていますが，ここではEngelund [Ref:38] による2次流分布式を以下に示します． 式の誘導はAppendix V ( Appendix V (Engelundによる主流および2次流の流速分布式) )を参照下さい．

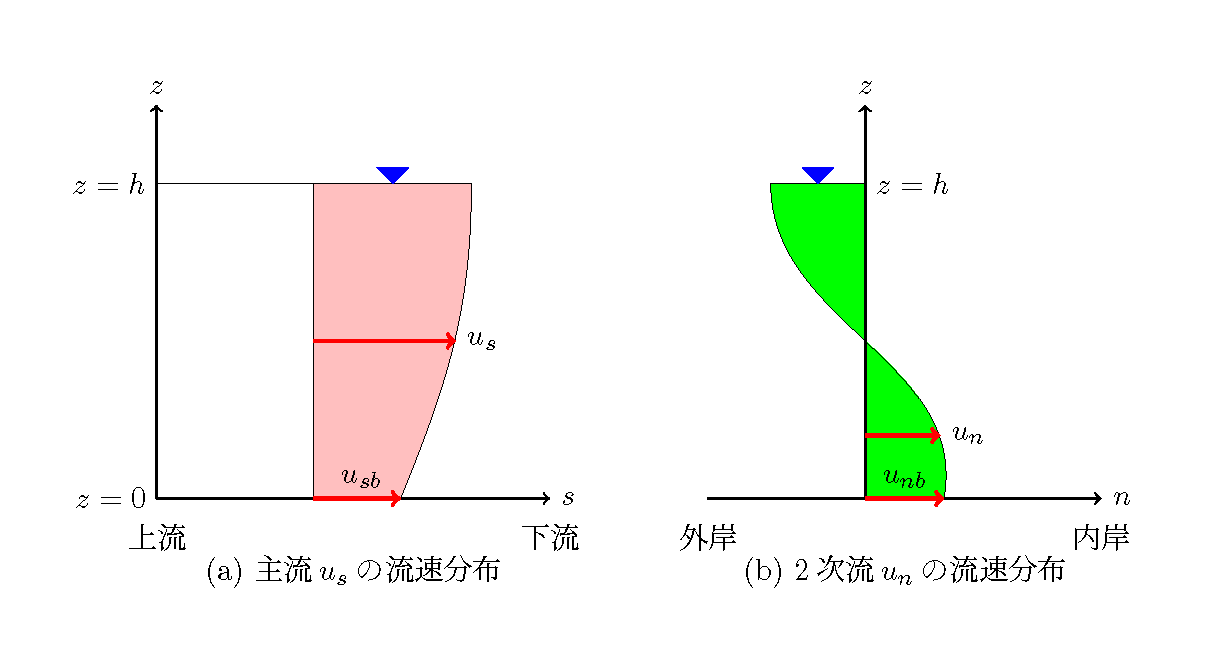
Figure 120 : 主流と2次流の流速分布

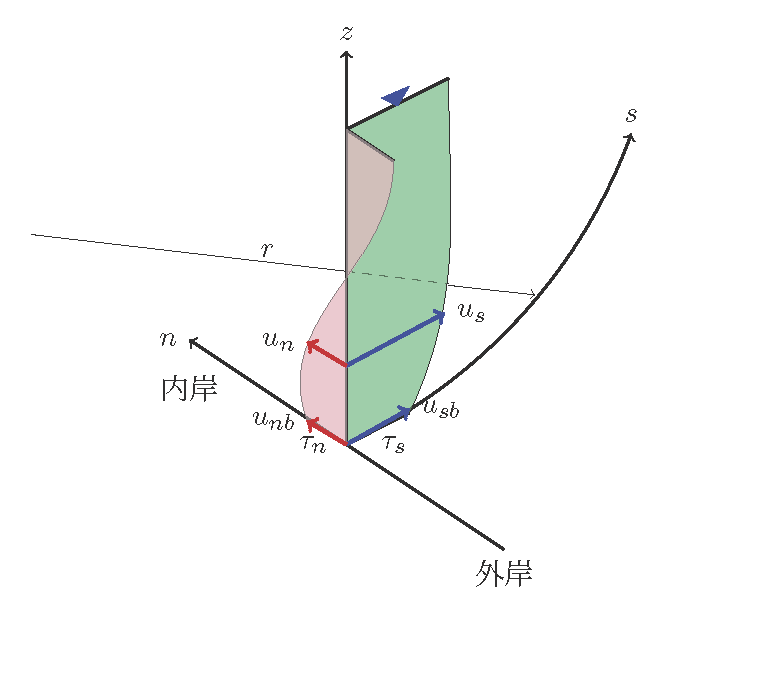
Figure 121 : 主流と2次流の流速分布(3次元表示)

主流の鉛直方向流速分布(放物線分布)

(277)\[u_s(\zeta)=<u_s>\cfrac{\chi+\zeta-\cfrac{\zeta^2}{2}}{\chi_1}\]

ただし, \(u_s\) は流下方向流速, \(<u_s>\) は \(u_s\) の水深 平均値, \(zeta\) は河床からの無次元距離で次式で表されます．

(278)\[\zeta=\cfrac{z-z_b}{h}\]

ただし, \(z\) は河床からの距離, \(z_b\) は河床高, \(h\) は水深です. また, \(\chi\) および \(\chi_1\) は定数で，これらの算定方法は こちら を参照下さい.

2次流の流速分布(6次関数分布)

(279)\[u_n(\zeta)=A_n f_n, \; \; f_n=\cfrac{G_0(\zeta)}{C_f \chi_1}\]

ただし, \(u_n\) は横断方向流速, \(A_n\) は次式で表される,

(280)\[ \begin{align}\begin{aligned}A_n & = <u_s>\cfrac{h}{r_s}\\G_0(\zeta) & =\cfrac{1}{{\chi_1}^2}\left[ -\left(\chi^2+\cfrac{2}{3}\chi+\cfrac{2}{15}\right)\left(\zeta+\chi\right)+\cfrac{1}{2}\chi^2\zeta^2+\cfrac{1}{3}\chi\zeta^3 \right.\\& \left. +\cfrac{1}{12}\left(1-\chi\right)\zeta^4 -\cfrac{1}{20}\zeta^5+\cfrac{1}{120}\zeta^6 \right]+\chi_{20}\left(\cfrac{1}{2}\zeta^2-\zeta-\chi\right)\end{aligned}\end{align} \]

ただし,

(281)\[\chi_{20} = B = -\cfrac{1}{{\chi_1}^3} \left(\chi^3+\chi^2+\cfrac{2}{5}\chi+\cfrac{2}{35}\right), \: \: \cfrac{<u_s>}{u_\ast} = \cfrac{1}{\sqrt{C_f}}, \; \chi=\chi_1-\cfrac{1}{3}\]

なお, (279) , (280) , (281) に現れる諸変数については こちら を参照してください．

2次流強度

(277) 式および (279) 式で \(\zeta=0\) (底面) とし， それぞれ \(s\) 方向および \(n\) 方向の底面流速として， それらの比をとり次式で表します．

(282)\[u_{nb}= u_{sb} N_\ast \cfrac{h}{r}\]

ここで，\(u_{sb}\) および \(u_{nb}\) はそれぞれ \(u_s\) および \(u_n\) の底面における値です ( Figure 120 参照). また, \(r\) および \(h\) は 流路の曲率半径と水深です. また，\(N_\ast\) は (512) に示すような一様湾曲流を想定する係数 で, 2次流強度について に示すように標準的な値を用いると \(N_\ast \approx 7\) と なります．

なお, (282) 式は実際は,

(283)\[u_{nb}= |u_{sb}| N_\ast \cfrac{h}{r}\]

となります．なぜなら2次流の駆動力となる, (276) 式による \(F_s\) は 主流 \(u_s\) の2乗に比例するので，\(u_s\) の符号には無関係となるためです.

掃流砂の方向も，底面流速の方向に一致すると考えると, 次式が成立します．

(284)\[q_{bn}= |q_{bs}| N_\ast \cfrac{h}{r}\]

ここで，\(q_{bs}, q_{bn}\) は \(s, n\) 方向の掃流砂量です.

(284) 式によれば，一様湾曲流路において 流線方向に掃流砂量が存在する場合, 外岸から内岸に向かう横断方向流砂量が生じ,その大きさは水深 \(h\) に比例し, 同心円状の流れの曲率半径 \(r\) に反比例するということが分かります． この内岸に向かう掃流砂により 湾曲流路では外岸の土砂が内岸に運ばれ，内岸に砂州が発生することになりま

流線の曲率について

以上の説明は一様湾曲流の2次流についてについてですが, 一般の蛇行水路ではどうでしょうか？ Figure 119 のような一様湾曲流では流線が水路に平行なので，流線も水路に平行の同心円 となり曲率半径はこの同心円の半径となります． ところが，Figure 112 のような蛇行水路の場合，流線は明らかに水路に平行には ならず，水路形状とは位相差を伴った異なった線形になります．

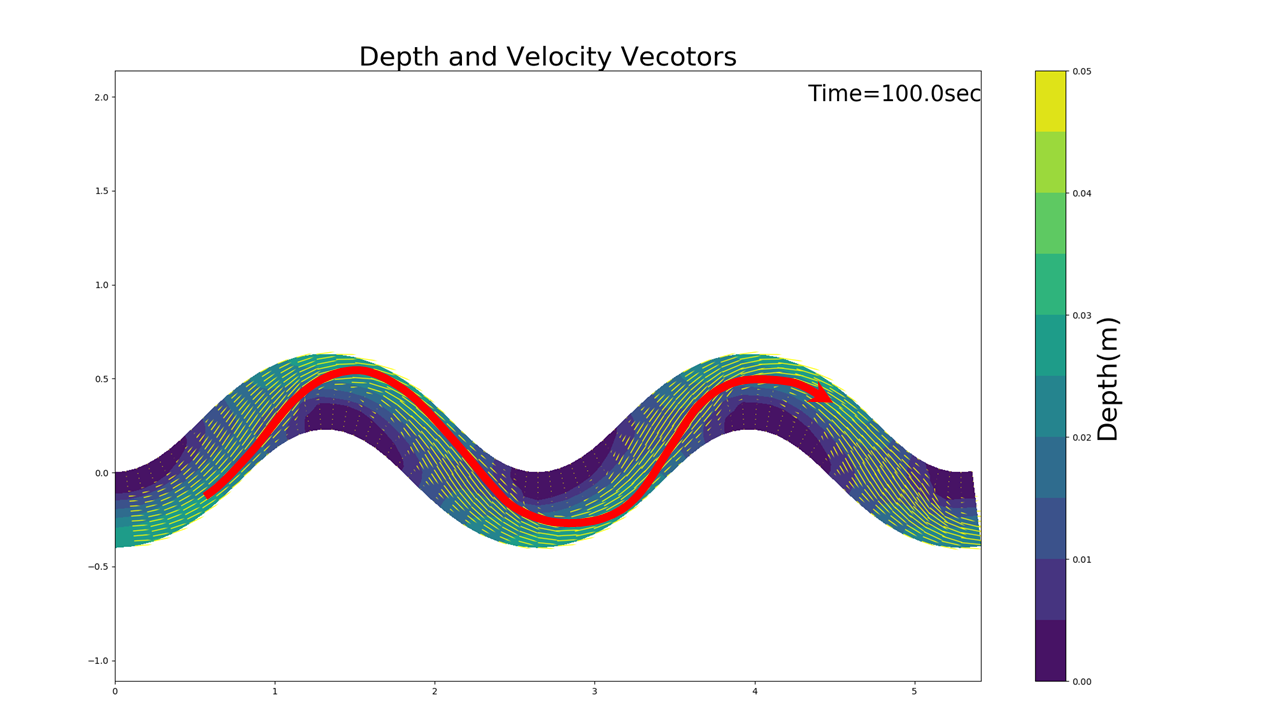
Figure 122 : 蛇行水路における流線

Figure 122 は計算結果のベクトル図に目視で凡その流線を描いて見たもので， 実際の流線はおそらくこのような形になると予想されます． この流線(正確には水深平均流の流線)に沿ってはこれを横切る流れは生じないので， この流線の形が正確に求まれば，この流線を Figure 121 の:math:s 軸と 見なせば2次流もこの流線に直交する成分として, 上記の理論式を適用することが出来ます． 以下に，この「水深平均流の流線( Figure 122 の赤線)」の算定法を解説します．

流線の曲率の算定法

注釈

ここでの流線とは水深平均流速の流線のことで，2次元平面上での流線です． 流線の算定には水深平均流速を用いることにりますので，以降の記述で出てくる, \(u_x, u_y, u_s, u_n\) などは水深平均流速です．

直交直線座標の場合

まずは話を単純化するために，直交直性座標( \(x-y\) 座標)の場合について考えてみます．

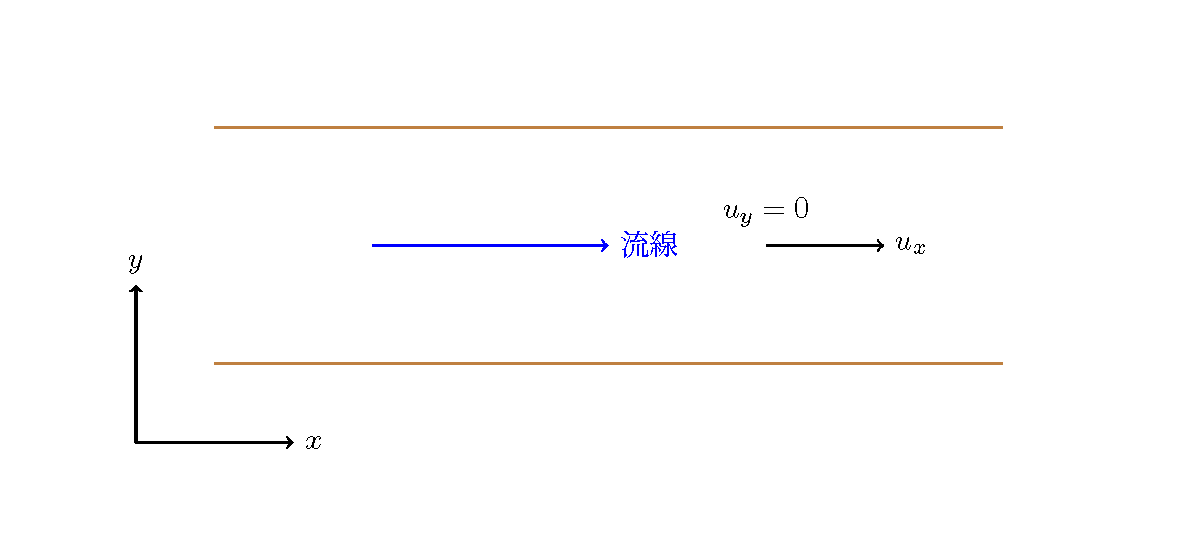
Figure 123 : 直線水路で直線状の流線

直線流路での流れが Figure 123 のようにまっすぐな場合は流線は流路と同じく真っ直ぐで 曲率はゼロ(曲率半径は無限大 \(\infty\)) です．

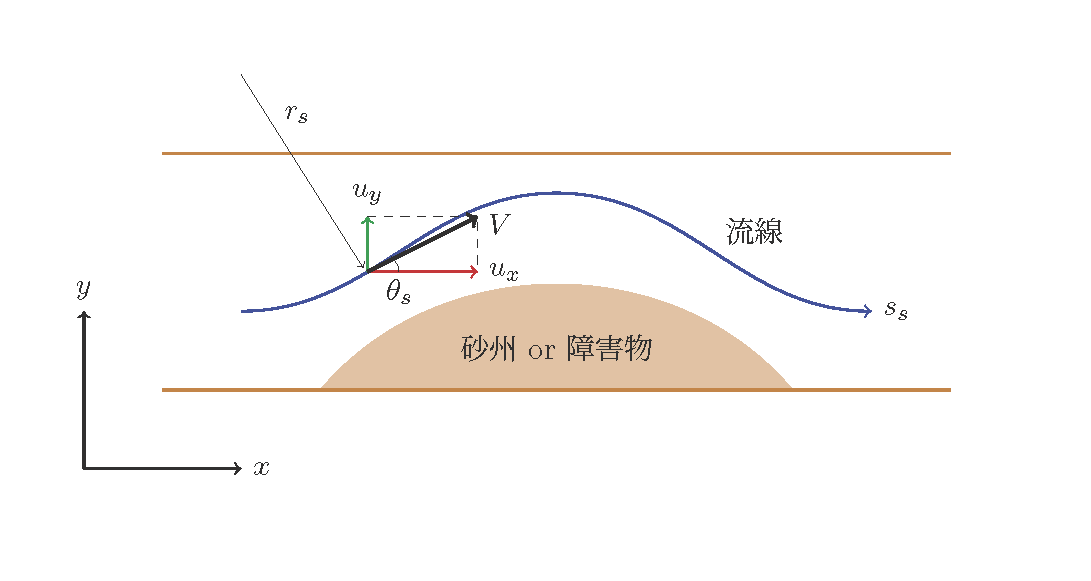
Figure 124 : 直線水路で曲がった流線

では, Figure 124 のように流路が真っ直ぐでも砂州や障害物などの影響で流線が曲がる ような場合を想定してみます．この時には流線の曲がりによって遠心力が発生し前述の 一様湾曲水路と同様に2次流が発生します． 今, Figure 124 に示すように, 新たに流線に沿った座標軸 \(s_s\) を定義し, これの曲がりによる曲率半径を \(r_s\) とすると \(r_s\) は次式で求める ことが出来ます．

(285)\[{1 \over r_s} ={{\partial \theta_s}\over{\partial s_s}}\]

ここに，\(\theta_s\) は \(s\) 軸と \(x\) 軸のなす角度で, 次式で表されます.

(286)\[\theta_s= \tan^{-1}\left( u_y \over u_x \right)\]

ただし, \(u_x\) および \(u_y\) はそれぞれ \(x\) および \(y\) 方向の流速です.

(287)\[{1 \over r_s} = {\partial \over {\partial s_s}} \left [\tan^{-1} (T) \right] = {\partial \over {\partial T}} \left [\tan^{-1} (T) \right]{{\partial T}\over{\partial s_s}} ={1 \over {1+T^2}} {{\partial T}\over{\partial s_s}}\]

ここで, \(T=u_y/u_x\) です. さらに, \(V=\sqrt{u_x^2+u_y^2}\) として,

(288)\[{1 \over {1+T^2}} = {1 \over {1+\left(\displaystyle{u_y \over u_x} \right)^2}} ={u_x^2 \over {u_x^2 + u_y^2}} = {u_x^2 \over V^2}\]

(289)\[{{\partial T}\over{\partial s_s}} = {\partial \over {\partial s_s}} \left(\displaystyle{u_y \over u_x} \right) = \displaystyle{{u_x \displaystyle{{\partial u_y}\over{\partial s_s}} -u_y \displaystyle{{\partial u_x}\over{\partial s_s}} }\over{u_x^2}}\]

(290)\[{\partial \over{\partial s_s}} = {{\partial x}\over{\partial s_s}} {\partial \over {\partial x}} +{{\partial y}\over{\partial s_s}} {\partial \over {\partial y}} ={u_x \over V} {\partial \over {\partial x}} +{u_y \over V} {\partial \over {\partial y}}\]

ただし, \(V=\sqrt{u_s^2+u_n^2}\) です. これより, 流線の曲率 \(1/r_s\) は,

(291)\[\begin{split}{1 \over r_s} = \cfrac{1}{1+T^2}\cfrac{\partial T}{\partial s_s} =\cfrac{u_x^2}{V^3} \left\{ \cfrac{\partial u_y}{\partial x}+\cfrac{u_y}{u_x}\cfrac{\partial u_y}{\partial y} -\cfrac{u_y}{u_x}\cfrac{\partial u_x}{\partial x}-\cfrac{u_y^2}{u^2}\cfrac{\partial u}{\partial y} \right\} \\ ={1 \over V^3} \left\{ u_x^2 \cfrac{\partial u_y}{\partial x} -u_y^2 \cfrac{\partial u_x}{\partial y} +u_x u_y \left(\cfrac{\partial u_y}{\partial y}-\cfrac{\partial u_x}{\partial x} \right) \right\}\end{split}\]

となり, 流線の曲率半径は各点の局所的な流速だけで求めることが可能となります．

曲線座標の場合

次に，前節のSin-Generated-Curveのような直交曲線座標の場合を考えて見ましょう．

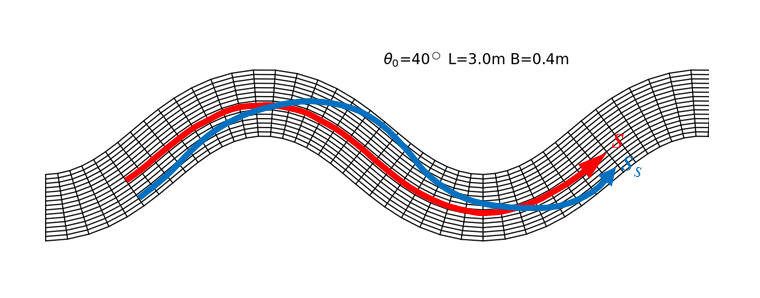
Figure 125 : 流路の曲率と流線の曲率(1)

Figure 125 のように，流線の曲率が流路の曲率 からずれる場合を想定します．赤矢印が水路に沿った座標軸で青矢印が流線です．

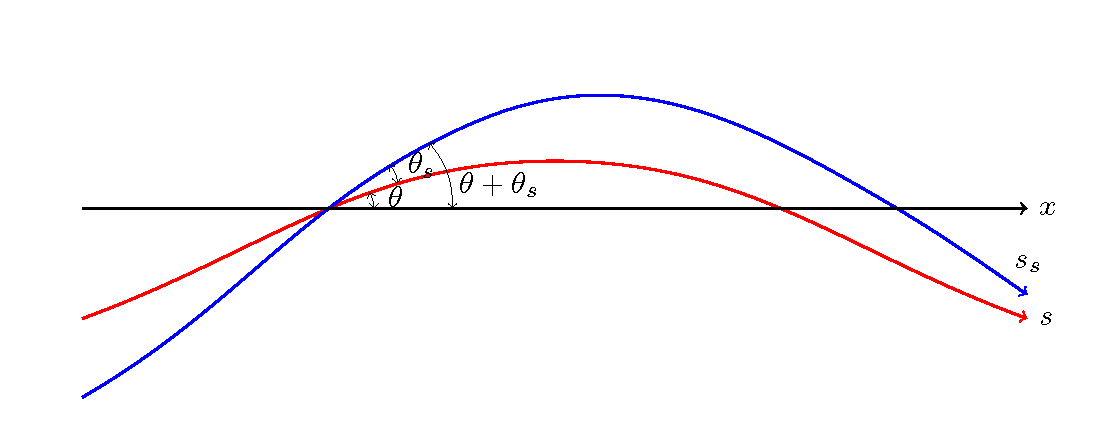
Figure 126 : 流路と流線の曲率とその角度

Figure 126 に示すように，流路に沿った座標軸 \(s\) の \(x\) 軸に対する角度を \(\theta\) , \(s\) 軸と流線の方向 の間の角度を \(\theta_s\) とすると, 流線の \(x\) 軸に対する角度は, \(\theta+\theta_s\) となり，流線の曲率は次式となります．

(292)\[\cfrac{1}{r_s}=\cfrac{\partial}{\partial s}\left( \theta+\theta_s\right)= \cfrac{\partial \theta}{\partial s} +\cfrac{\partial \theta_s}{\partial s}\]

ここで, \(\cfrac{\partial \theta}{\partial s}\) のほうは前述の Sin-Generated Curve や Kinoshita-Generated Curve のように, \(\theta\) が \(s\) の関数式で与えられる場合はそれを微分したものを, 実河川のように任意形状の場合は 曲率の算定法 で示した方法で算定したものを用います． なお，当然ですが直線の場合は \(\cfrac{\partial\theta}{\partial s}=0\) , Figure 119 のような一様湾曲流の場合は対象とする同心円の曲率半径の逆数となります． また，要注意点としては, 例えば Sin-Generated Curveの曲率である (257) 式は 流路中心線上の曲率であり，対象点の横断線の位置によって補正が必要になるということです．

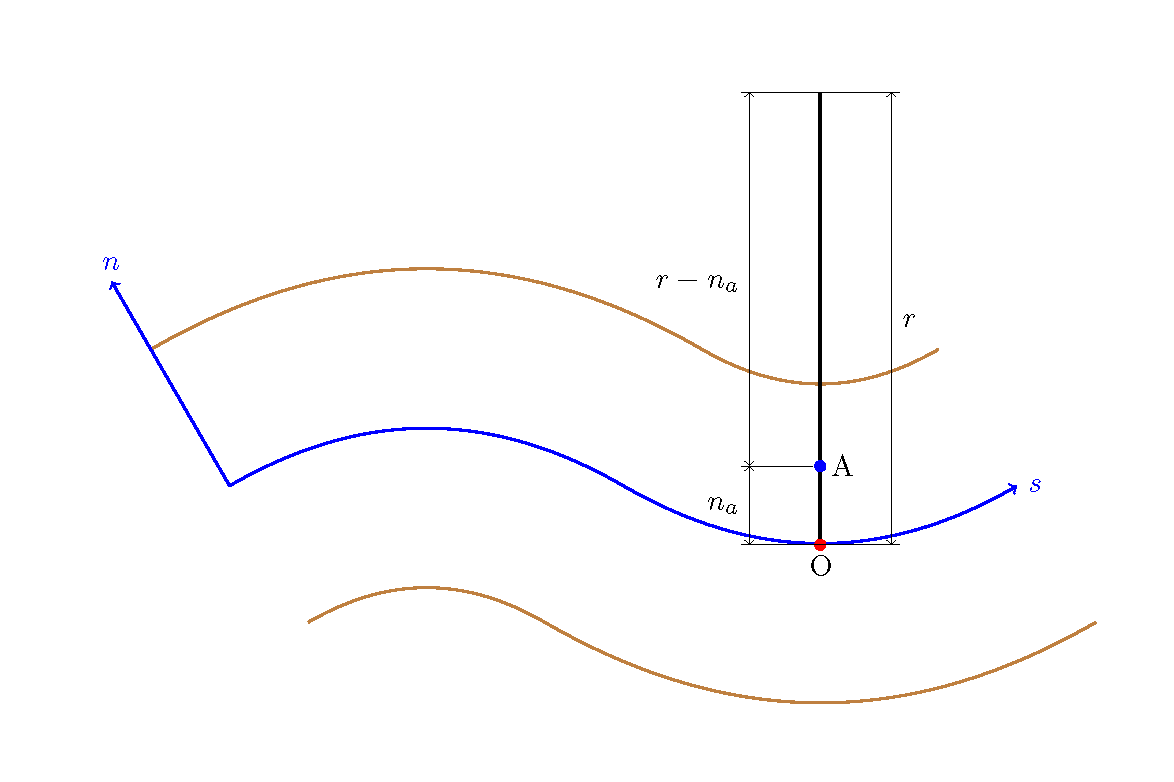
Figure 127 : 曲率半径の補正

Figure 127 の例でO点は流路中心線上にありますので，\(r\) の補正は必要ありませんが． O点より \(n_a\) だけ左岸側に離れた A 点では \(r\) の替わりに \(r-n_a\) を 用いる必要があります．

(292) 式右辺第2項の \(\cfrac{\partial \theta_s}{\partial s}\) については， 流路に沿った座標軸方向からの偏倚成分の曲率なので，\(x-y\) 座標において 誘導した (291) 式で，\(u_x, u_y\) の替わりに \(u_s, u_n\) を用いて,

(293)\[\cfrac{\partial \theta_s}{\partial s} ={1 \over V^3} \left\{ u_s^2 \cfrac{\partial u_n}{\partial s} -u_n^2 \cfrac{\partial u_s}{\partial n} +u_s u_n \left(\cfrac{\partial u_n}{\partial n}-\cfrac{\partial u_s}{\partial s} \right) \right\}\]

となります．なお，前記と同様に, (293) 式は流路中心線上の場合であり， 計算対象点の中心線からの距離によって補正が必要になります．

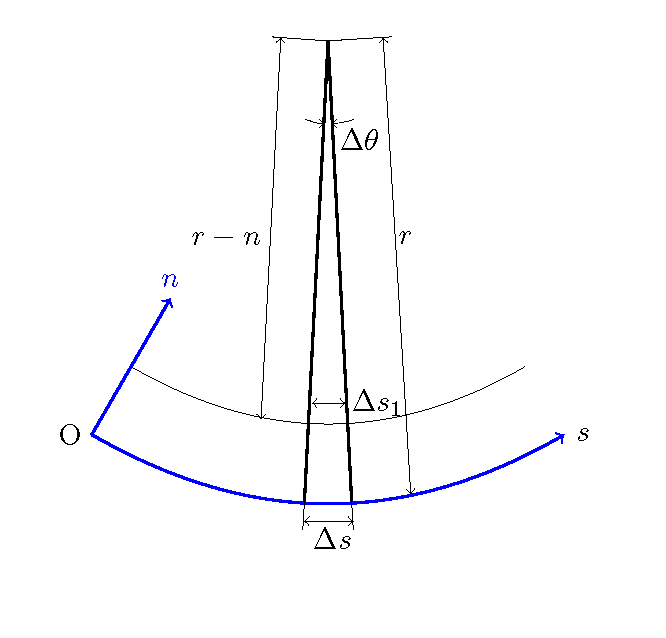
Figure 128 : \(\Delta s\) の補正

Figure 128 より,

(294)\[ \begin{align}\begin{aligned}r \Delta \theta = \Delta s, \hspace{1cm} & (r-n)\Delta \theta = \Delta s_1\\\cfrac{r-n}{r}\Delta s = \Delta s_1, \hspace{1cm} & \cfrac{1}{\Delta s_1} =\cfrac{1}{\Delta s}\cfrac{r}{r-n}\end{aligned}\end{align} \]

したがって, (293) 式において, \(\cfrac{1}{\partial \theta}\) を, \(\cfrac{r}{r-n} \cfrac{1}{\partial \theta}\) に置き換えることにより，任意の点における 流線の曲率を表すことが出来ます. すなわち,

(295)\[\cfrac{r}{r-n} \cfrac{\partial \theta_s}{\partial s} ={1 \over V^3} \left\{ u_s^2 \cfrac{r}{r-n} \cfrac{\partial u_n}{\partial s} -\cfrac{\partial u_s}{\partial n} u_n^2 +u_s u_n \left(\cfrac{\partial u_n}{\partial n}-\cfrac{r}{r-n} \cfrac{\partial u_s}{\partial s} \right) \right\}\]

流線の曲率の計算例

Sin-Generated Curveの例

波長 \(L\) = 3m, 水路幅 \(B=\) 0.4m, 最大蛇行角 \(\theta_0=40^\circ\) 勾配 \(I\) =0.001 のSin-Generated Curveに, (255) 式で 最大砂州波高 \(A_p\) = 0.015m, 位相差 \(\delta\) =0.2m の砂州状地形を 設置し, マニングの粗度係数 \(n_m\) = 0.02 として, 流量 \(Q\) =0.001m \(^3\) /sを流した場合の2次元計算を行った結果の 水深コンターと, 水深平均流速ベクトルを下図 Figure 129 に示します．

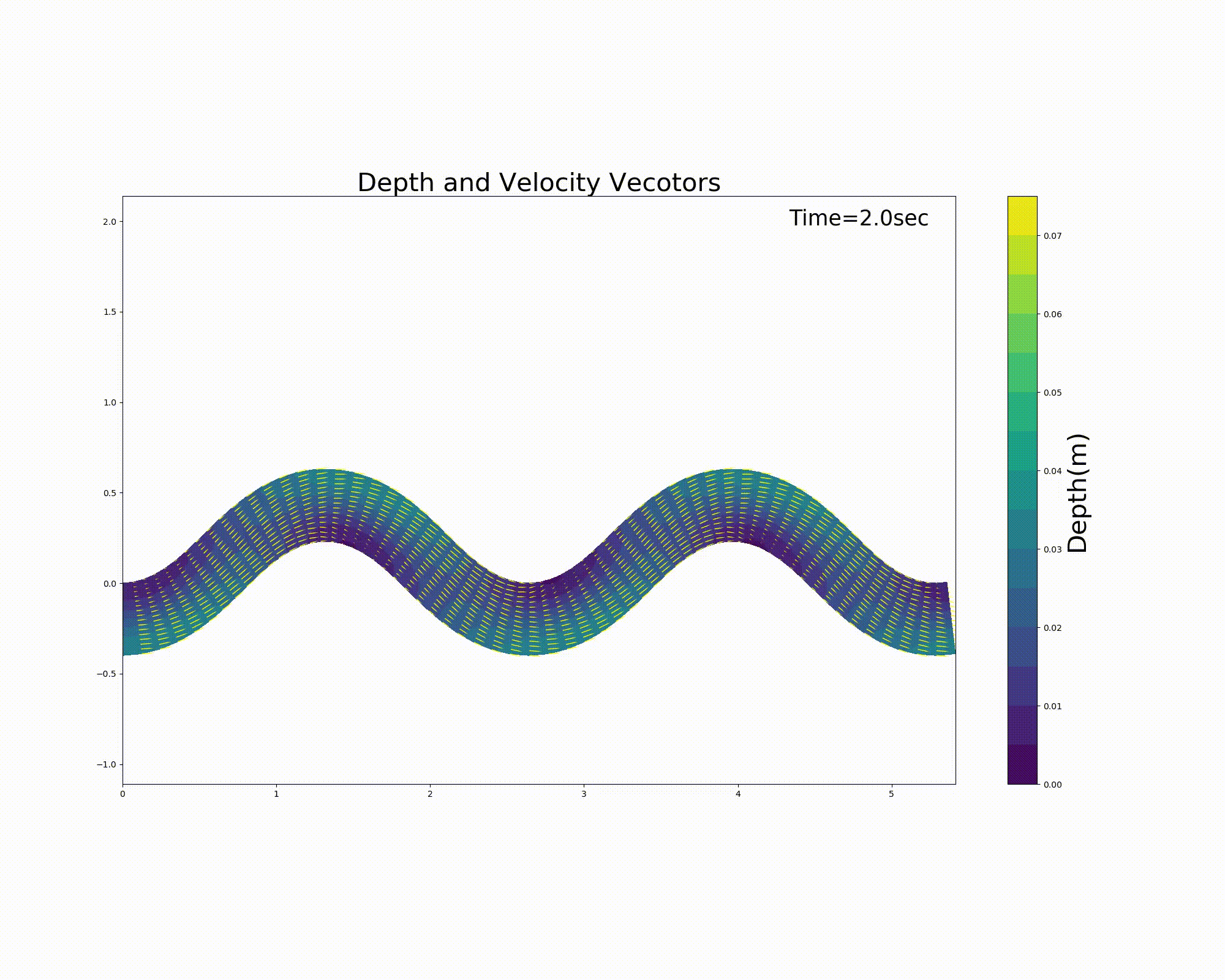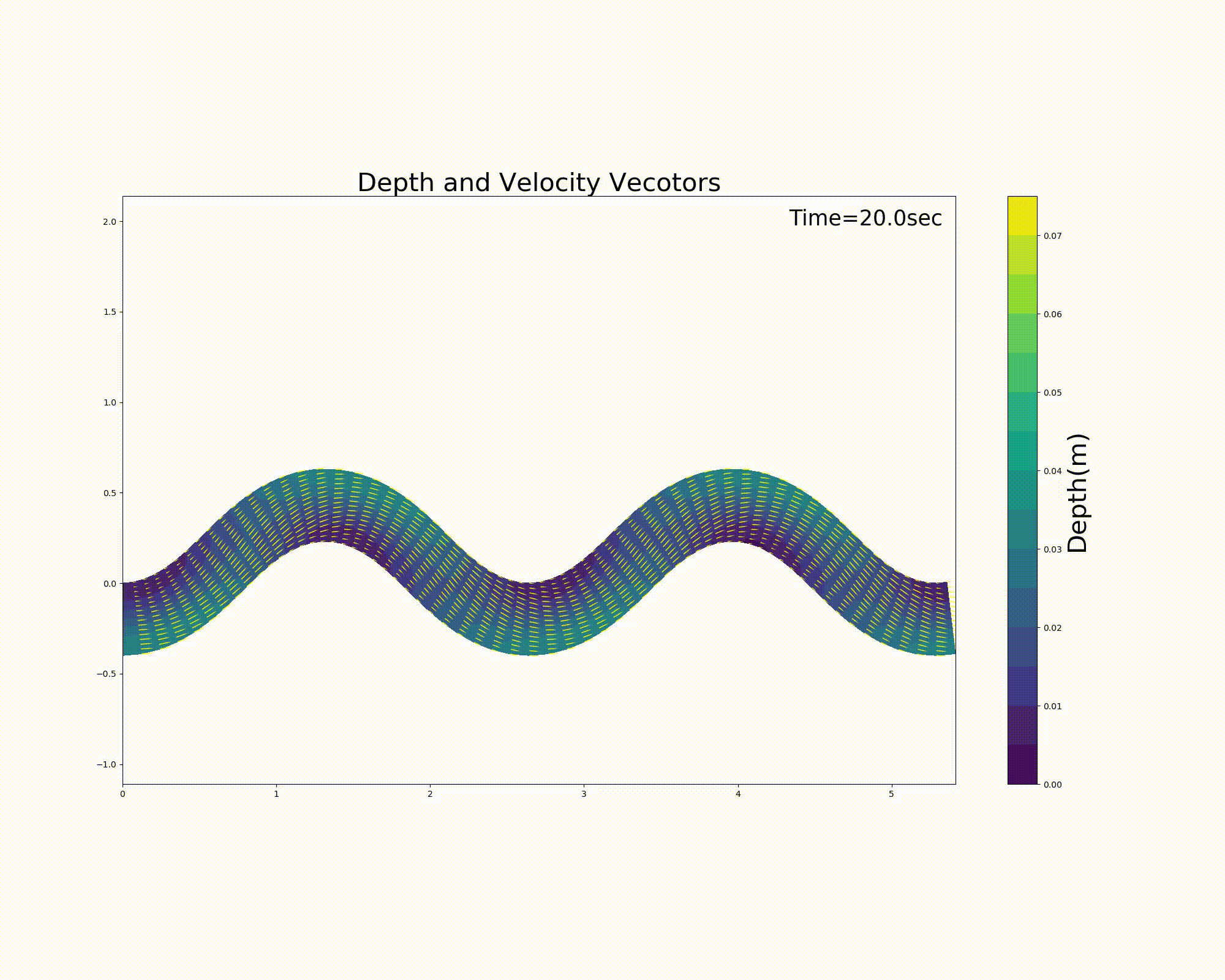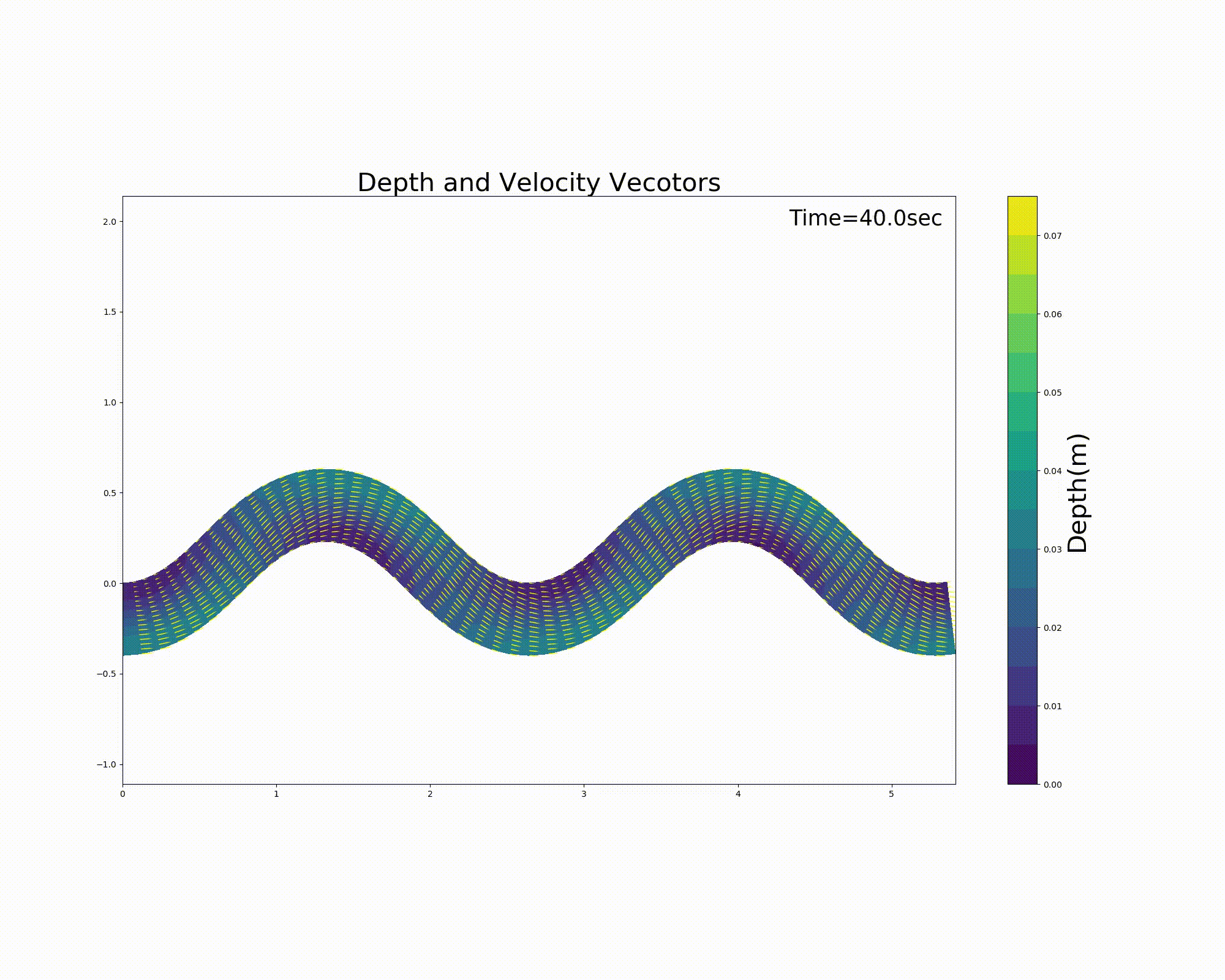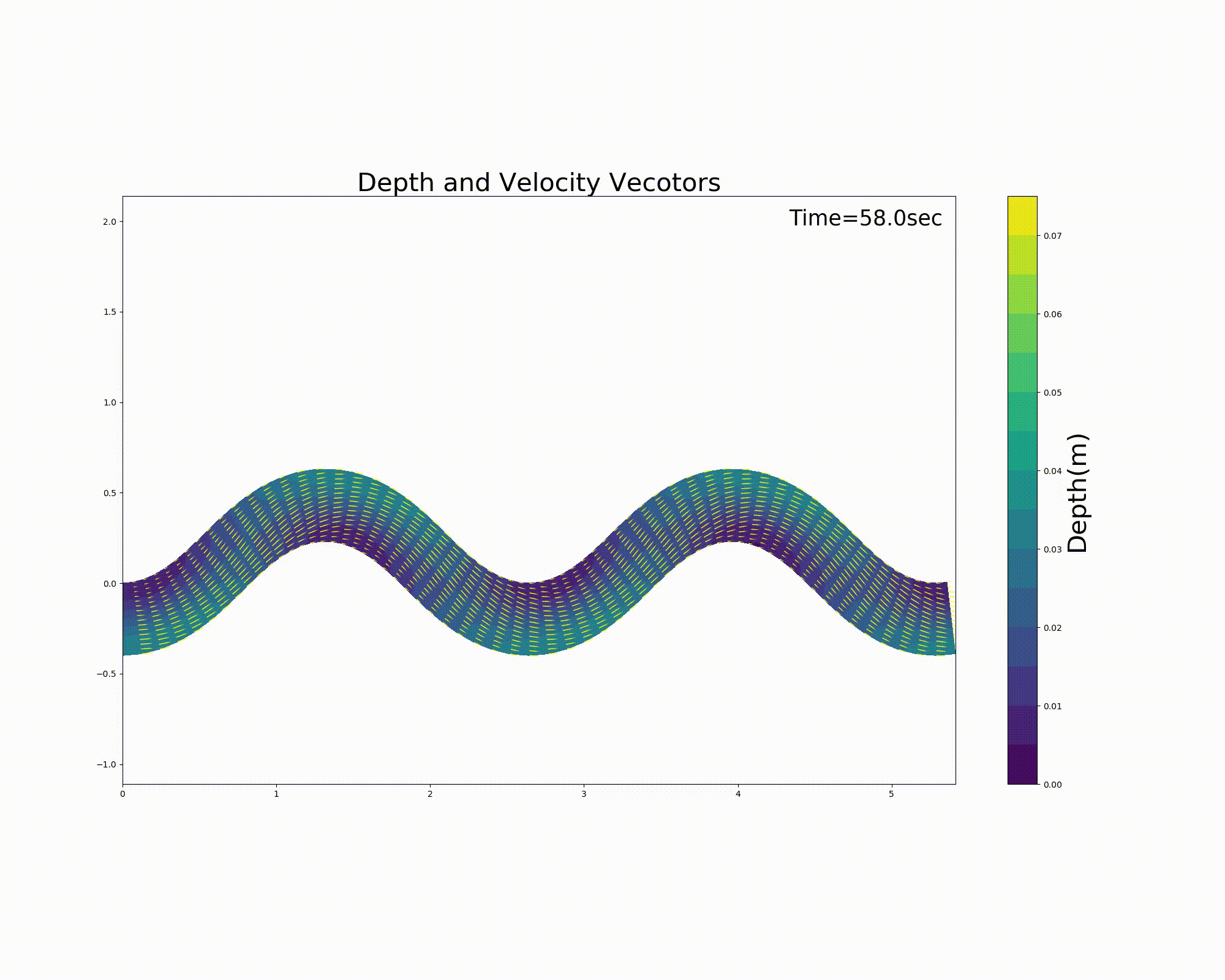
Figure 129 : Sin-Generated Curveでの流れの計算例

この時の水路中心線に沿った曲率 \(1/r\) と，水路中心線に沿った 水深平均流速の流線の曲率 \(1/r_s\) を下図 Figure 130 に示します． なお，\(1/r_s\) は (292) で計算し, \(\cfrac{\partial \theta_s}{\partial s}\) は (293) 式で計算したものの 水路中心線に沿ったものです．(293) に現れる偏微分項はすべて中央差分で計算してあります．

計算開始直後に若干不安定になりますが, その後安定し, 流線の曲率は水路の曲率に対して 若干振幅が大きくなり流下方向に僅かな位相差を持った形で安定しているのが分かります． 曲率が大きくなるということは，曲率半径が小さくなるということで，流線のカーブの曲がり 度会いが水路の曲がりに対して位相差を持ちながら下流に伝わるというイメージどおり の結果が得られています．

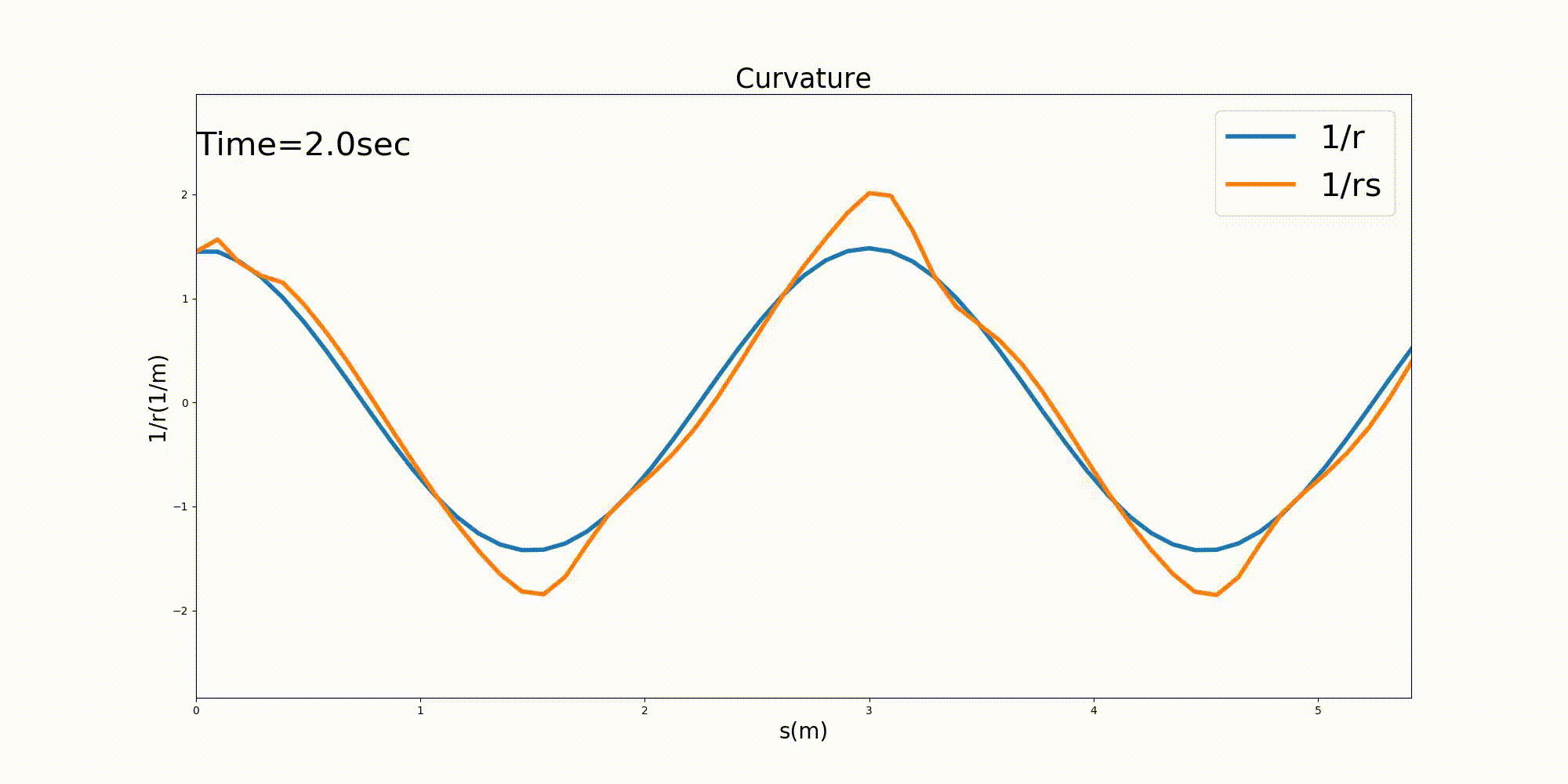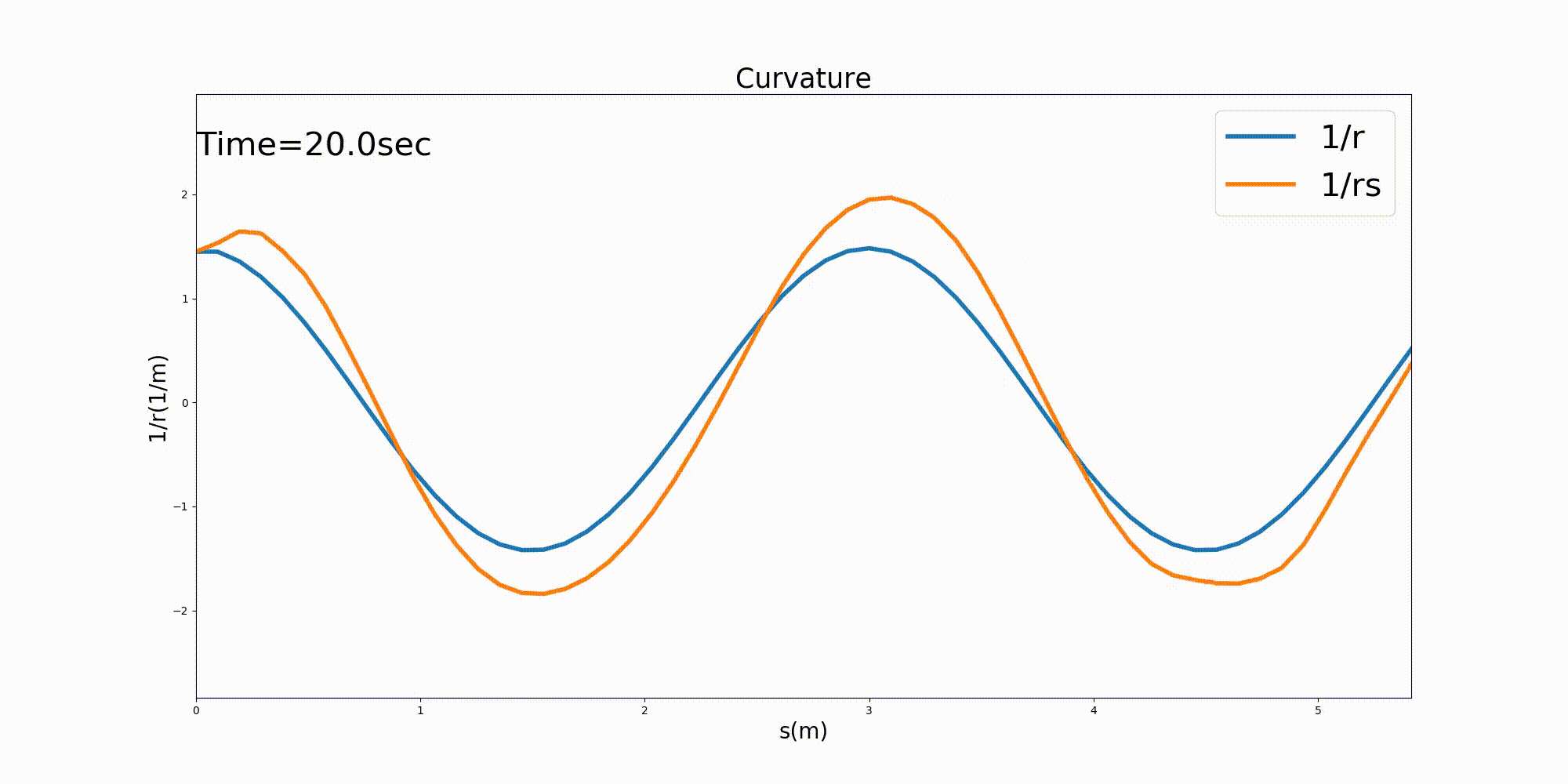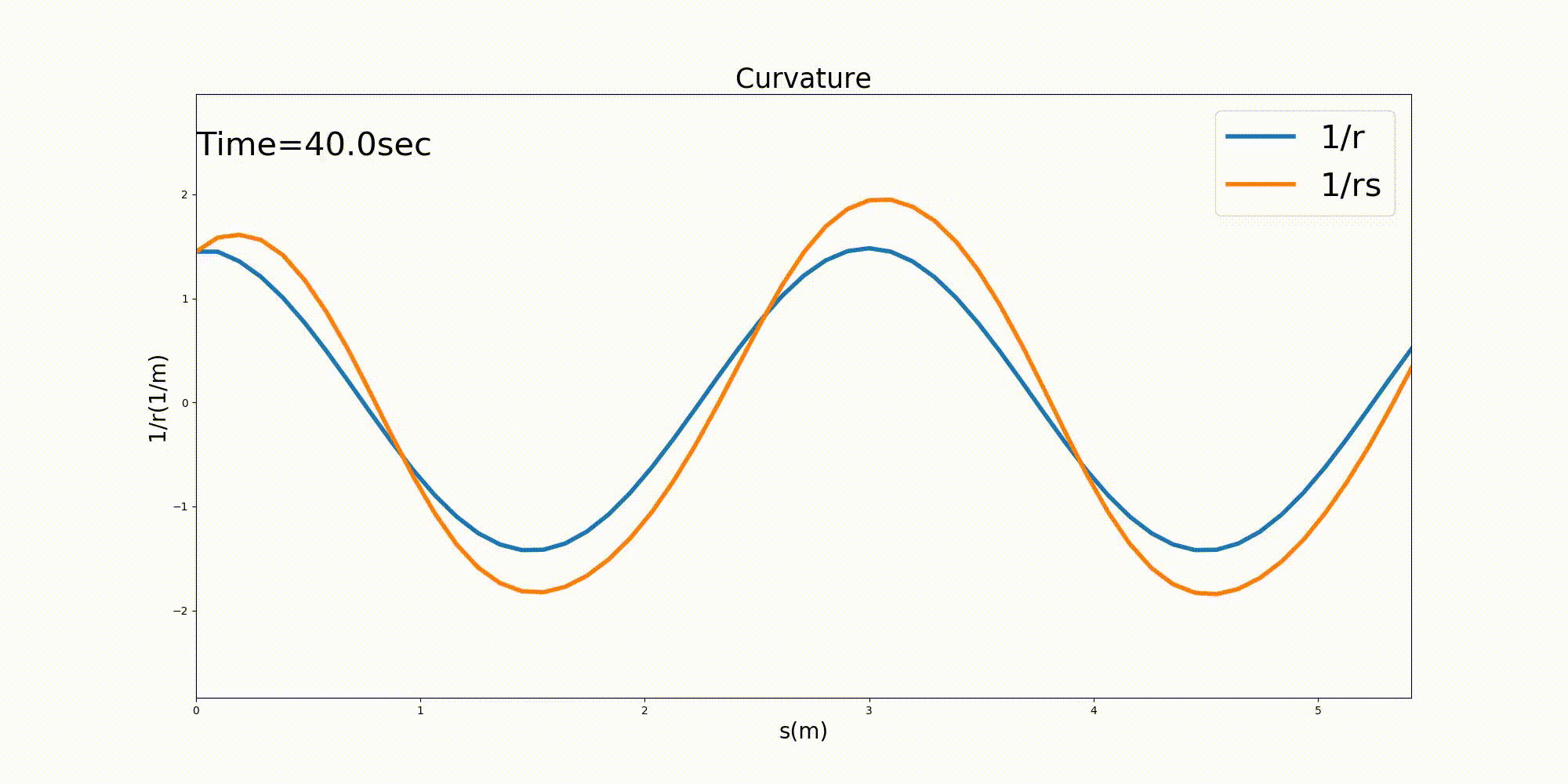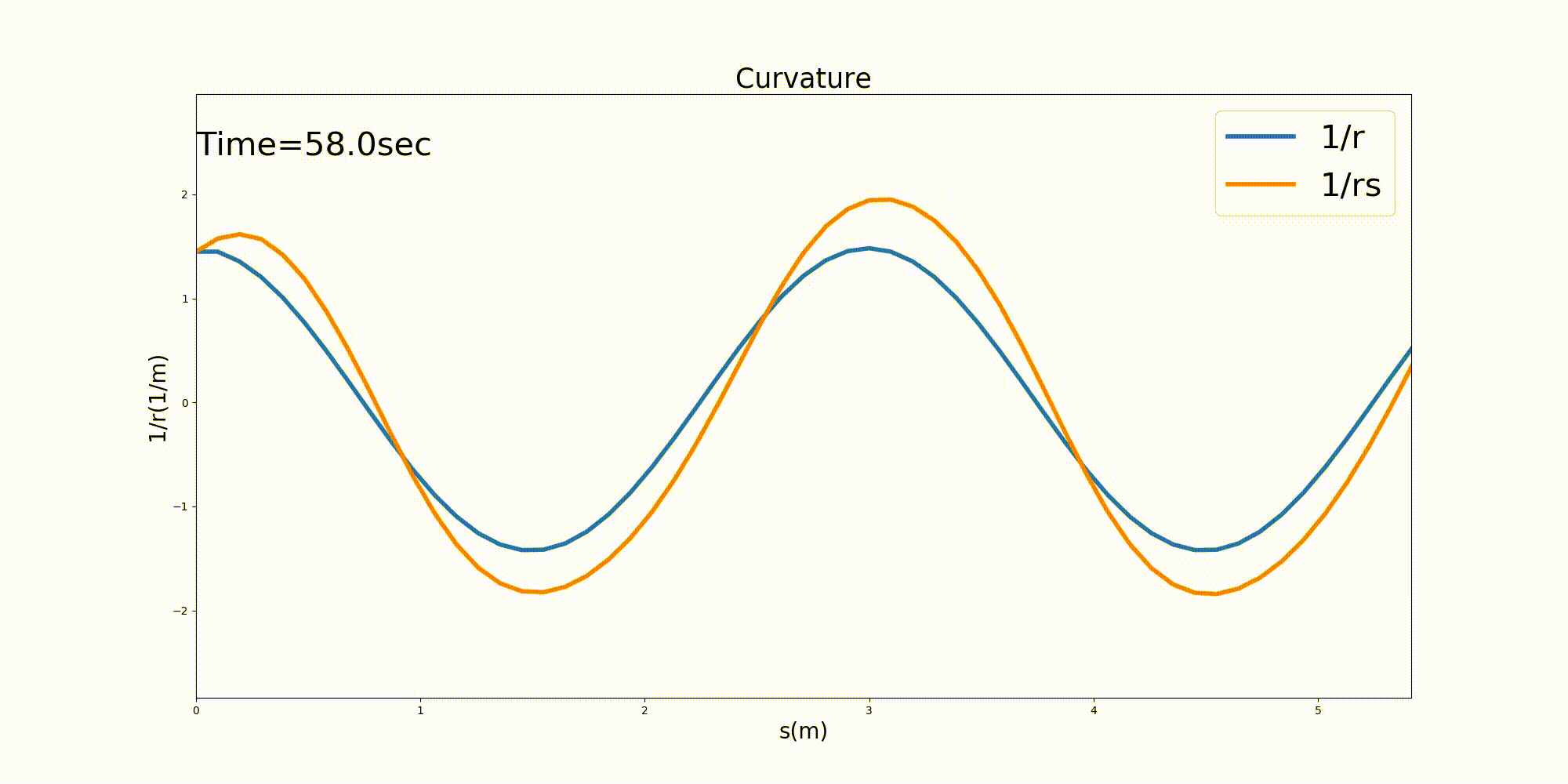
Figure 130 : Sin-Generated Curveでの流路の曲率と，流線の曲率

水制群を含む直線水路における計算例

蛇行水路の場合は最初から流路に沿った流れの曲率が発生しますが，直線水路でも， 障害物などがれば流れが曲げられることによって流線に曲率が生じます． 例えば， Figure 131 のように直線流路の左右岸に水制を交互に配置して， 流れを強制的に蛇行させた場合にも流線の曲率が発生します．

Figure 131 は， 水路長 \(L\) = 4m, 水路幅 \(B=\) 0.4m, 勾配 \(I\) =0.001 の直線水路に長さ12cmの水制を 左右千鳥に80cm間隔で設置した場合の流れの計算結果で，水制の影響で水路は直線 であっても流れが左右に蛇行を繰り返しているのが分かります．

Figure 131 : 水制群を含む直線水路における流れ(流速ベクトル)

Figure 132 は上記の流れ場の計算結果より計算した，水深平均 流速による流線の曲率で，水路中央の値を縦断的にプロットしたものです． 青線は計算格子から求まる座標の曲率，オレンジ線は流速から求めた流線の曲率です． 直線水路で \(s\) 軸が直線ですので当然ながら格子の曲率(青線)はゼロですが， 流線の曲率は流れの蛇行に伴って左右に非定常な分布を示しています． この，流線の曲率によって，前述の蛇行水路同様に２次流が発生し，河床変動に 影響を及ぼすことが想定されます． ちなみに，この時の流量，水路中央の流速，中心線および左右岸に沿った水位の縦断 分布を Figure 133 に示します．

Figure 132 : 水制群を含む直線水路における流れ(流路と流線の曲率)

Figure 133 : 水制群を含む直線水路における流れ(流量・流速・水位縦断)

上記，水制を含む流れの計算は，前述のコード

https://github.com/YasuShimizu/Nays2d_sn_python

において，config.yml の替りに 同じレポジトリ内の config_groyne.yml を用いることにより計算されます．config.ymlファイル中で，水路形状や水理条件の 他に水制の間隔・長さ・配置方法なども設定できます．

https://github.com/YasuShimizu/Nays2d_sn_python/blob/main/config_groyne.yml

config_groyne.ymlの内容:

j_rep: 0 # 周期境界条件 0:周期境界条件無 1:周期境界条件

lam : 2.0 # 水路の波長(m)
nx0 : 41 # 格子数/1波長
ny : 21 # 横断方向格子数(奇数推奨)
wn : 2 # 波数
chb : 0.4 # 水路幅(m)
t0_degree : 0 # 最大蛇行偏角(Degree)
slope: 0.001 # 水路勾配
xsize: 20 # 計算結果をプロットする図の横スケール

amp : 0.0 # 初期河床砂州の波高(m)
delta : 0. # 初期河床砂州の位相差(m)
beta_0: 0. # 内岸で川幅を狭める割合
amp_0: 0.0 # 狭めた部分の河床高さ(m)

snu_0 : 1e-6 # 動粘性係数
hmin : 0.001 # 最小水深(m)
cw: 0.001 # 側壁摩擦係数
ep_alpha: 1. # 渦動粘性係数の係数

qp: 0.001 # 流量(m^3/s)
snm: 0.01 # マニング粗度
g: 9.8 # 重力加速度(m/s^2)

j_west: 0 # 上流条件(0:開放, 1:閉鎖)
j_east: 0 # 下流条件(0:開放, 1:閉鎖)
j_hdown: 1 # 下流端水位条件(0:自由流出, 1:等流水深, 2:固定水位を与える)
h_down : 1. # j_hdown=2 の時の固定水位(m)
j_inih: 2 #初期水位縦断 0:直線 1:等流計算 2:不等流計算

alh: 0.6 # 水位収束計算のReluxsation係数
lmax: 20 # 各タイムステップでの水位収束計算最大回数

etime: 60. # 計算終了時間(sec)
tuk: 0.2 # 計算結果アウトプット間隔(sec)
dt: 0.01 # 計算タイムステップ(sec)
stime: 0. # アウトプット開始時間(sec)

j_obst: 1 # 障害物の有無 0=無 1=有
jo_type: 2 # 障害物設置方法 1=ファイルから読む 2=条件を指定する
jo_method: 4 # 0=無 1=右岸のみ 2=左岸のみ 3=左右岸(千鳥) 4=左右岸(同位置)
f_dike_pos: 0.5 # 最初の水制の位置(m)
dike_dis: 0.8 # 水制間隔(m)
dike_length: 0.12 # 水制長(m)
dike_thick: 0.02 # 水制厚(m)
num_dike : 4 # 水制本数(方岸当たり)

iskip: 1 # ベクトルプロットの i 方向間引き
jskip: 1 # ベクトルプロットの j 方向間引き
jscale: 15 # ベクトルのスケールファクター

alpha_upu : 0.05 # 周期境界条件の緩和係数

vcolor : yellow # ベクトルのカラー
rrmax: 6 # 曲率プロットの軸最大値(1/m)