この節の作者: 清水康行 <yasu@i-ric.org>

本テキストへの感想, 質問, 要望, バグ報告などはこちらへお願いします.

蛇行河川の河床変動計算(実践編)

2次元流砂量の算定方法

2次流による底面せん断力の方向

[本節の内容は西村ら [Ref:40] の論文に詳しく記載されています．]

水深平均流の流線に沿って, 流線方向に等流状態を仮定すると, 水深平均流速と底面せん断力の関係は, 抵抗則にマニング則を用いた 場合, (329) 式より,

(296)\[\tau=\rho g h I_e = {{\rho g n_m^2 V^2}\over{h^{1/3}}}\]

となります. ここで，\(V\) は流線方向の合成流速を想定してますので, \(s, n\) 座標 の場合, \(V=\sqrt{u_s^2+u_n^2}\) です. 流線方向に合成された無次元掃流力は次式となり,

(297)\[\tau_\ast=\cfrac{h I_e}{s d}=\cfrac{n_m^2 V^2}{s d h^{1/3}}\]

流線方向の掃流砂量は, この \(\tau_\ast\) を用いて, 前章の 流砂量式 で述べたような各種の掃流砂量式で求めることが可能で,これを \(q_b\) とします.

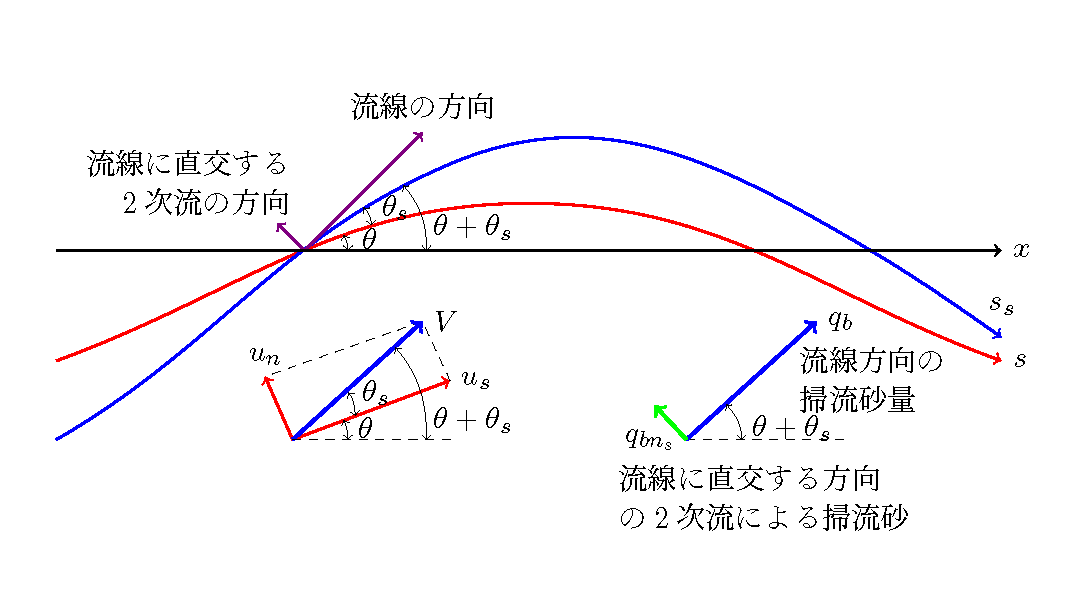
Figure 134 : 2次流を考慮した河床せん断力の方向

2次流による掃流砂量は，(284) が水深平均流の流線上でも成立すると考え, 次式で求めることが出来ます．

(298)\[q_{bn_s}= q_b N_\ast \cfrac{h}{r_s}\]

ただし, \(q_{bn_s}\) は2次流による流線に直交する方向の掃流砂量, \(N_\ast\) は (512) 式の2次流強度(標準的には=7.0), \(r_s\) は流線の曲率半径です．

重力効果による補正

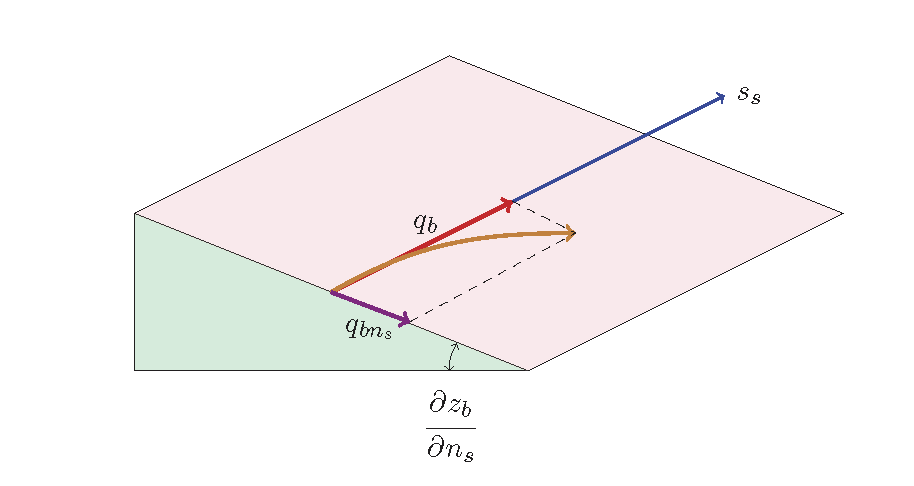
Figure 135 : 流砂量の斜面補正

Figure 135 に示すように, 流線方向に発生した掃流砂に対して 流砂の方向に交差する方向が斜面になっている場合，斜面方向に重力の斜面方向成分が働き， 流砂の方向が曲げられます．この, 横断方向の斜面の重力効果については, 前述の2次流による効果 を合わせて考慮した以下の長谷川の式 [Ref:27] が良く知られています.

(299)\[q_{bn_s}=q_b \left(N_\ast \cfrac{h}{r_s} -\sqrt{\cfrac{\tau_{\ast c}}{\mu_s \mu_k \tau_\ast}} \cfrac{\partial z_b}{\partial n_s}\right)\]

ここで, \(\mu_s, \mu_k\) はそれぞれ砂粒子の静止摩擦係数および動摩擦係数, \(\tau_{\ast c}\) は無次元限界掃流力( (211) ), \(\tau_\ast\) は無次元掃流力( (207) ), \(z_b\) は河床高, \(n_s\) は水深平均流速の流線に直交する方向です.

重力効果は横断方向だけではなく，縦断方向にも作用します. 渡邊ら [Ref:39] は，この効果を一般座標上で表す式を提案していますが， これを，水深平均流線の方向とこれに直交する2次流の方向で示したのが次式となります．

(300)\[ \begin{align}\begin{aligned}q_{bs_s} & =q_b \left\{ \cfrac{u_{sb}}{\sqrt{{u_{sb}}^2+{u_{nb}}^2}} - \sqrt{\cfrac{\tau_{\ast c}}{\mu_s \mu_k \tau_\ast}} \left( \cfrac{\partial z_b}{\partial s_s} + \cos{\phi}\cfrac{\partial z_b}{\partial n_s} \right) \right\}\\q_{bn_s} & =q_b \left\{ \cfrac{u_{nb}}{\sqrt{{u_{sb}}^2+{u_{nb}}^2}} - \sqrt{\cfrac{\tau_{\ast c}}{\mu_s \mu_k \tau_\ast}} \left( \cfrac{\partial z_b}{\partial n_s} + \cos{\phi}\cfrac{\partial z_b}{\partial s_s} \right) \right\}\end{aligned}\end{align} \]

ただし, \(s_s, n_s\) は水深平均流速方向の座標およびこれに直交する座標軸, \(q_{bs_s}, q_{bn_s}\) は \(s_s, n_s\) 方向の単位幅掃流砂量, \(u_{sb}, u_{nb}\) は は \(s_s, n_s\) 方向の底面流速, \(\phi\) は \(s_s\) と \(n_s\) の間の角度で，本節の取り扱いでは \(\cos \phi = 0\) となります. なお, 通常は2次流流速は主流流速に比べ１オーダー以上小さい値となり, \({u_{nb}}^2 << {u_{sb}}^2\) なので,

(301)\[\sqrt{{u_{sb}}^2+{u_{nb}}^2} \approx |u_{sb}|\]

と見なすことが可能で, 横断方向の河床の流速に (283) 式を 適用すると (300) 式は

(302)\[ \begin{align}\begin{aligned}q_{bs_s} & =q_b \left( 1 -\sqrt{\cfrac{\tau_{\ast c}}{\mu_s \mu_k \tau_\ast}} \cfrac{\partial z_b}{\partial s_s} \right)\\q_{bn_s} & =q_b \left( N_\ast \cfrac{h}{r_s} -\sqrt{\cfrac{\tau_{\ast c}}{\mu_s \mu_k \tau_\ast}} \cfrac{\partial z_b}{\partial n_s} \right)\end{aligned}\end{align} \]

となります. \(\cfrac{\partial z_b}{\partial s_s}\), \(\cfrac{\partial z_b}{\partial n_s}\) については，

(303)\[ \begin{align}\begin{aligned}\cfrac{\partial z_b}{\partial s_s} =\cfrac{\partial s}{\partial s_s} \cfrac{\partial z_b}{\partial s}+ \cfrac{\partial n}{\partial s_s} \cfrac{\partial z_b}{\partial n} =\cfrac{u_s}{V}\cfrac{\partial z_b}{\partial s}+ \cfrac{u_n}{V}\cfrac{\partial z_b}{\partial n}\\\cfrac{\partial z_b}{\partial n_s} =\cfrac{\partial s}{\partial n_s} \cfrac{\partial z_b}{\partial s}+ \cfrac{\partial n}{\partial n_s} \cfrac{\partial z_b}{\partial n} =-\cfrac{u_n}{V}\cfrac{\partial z_b}{\partial s}+ \cfrac{u_s}{V}\cfrac{\partial z_b}{\partial n}\end{aligned}\end{align} \]

となります. \(s,n\) 座標上で河床変動計算を行う場合は, \(s,n\) 軸方向の 流砂量, \(q_{bs}, q_{bn}\) が必要になります. これらは, (302) 式で 得られた \(q_{bs_s}, q_{bn_s}\) を用いて以下の式で求められます．

(304)\[ \begin{align}\begin{aligned}q_{bs}=q_{bs_s} \cos\theta_s - q_{bn_s} \sin\theta_s = q_{bs_s} \cfrac{u_s}{V}-q_{bn_s}\cfrac{u_n}{V}\\q_{bn}=q_{bs_s} \sin\theta_s + q_{bn_s} \cos\theta_s = q_{bs_s} \cfrac{u_n}{V}+q_{bn_s}\cfrac{u_s}{V}\end{aligned}\end{align} \]

ただし, \(\cos \theta_s = \cfrac{u_s}{V}\), \(\sin \theta_s = \cfrac{u_n}{V}\) ( Figure 134 左下の図参照)．

したがって, (302) 式, (303) 式および (304) 式より,

(305)\[ \begin{align}\begin{aligned}q_{bs} & =q_b \left\{ \cfrac{1}{V} (u_s - u_n N_\ast \cfrac{h}{r_s}) -\sqrt{\cfrac{\tau_{\ast c}}{\mu_s \mu_k \tau_\ast}} \cfrac{\partial z_b}{\partial s} \right\}\\q_{bn} & =q_b \left\{ \cfrac{1}{V} (u_n + u_s N_\ast \cfrac{h}{r_s}) -\sqrt{\cfrac{\tau_{\ast c}}{\mu_s \mu_k \tau_\ast}} \cfrac{\partial z_b}{\partial n} \right\}\end{aligned}\end{align} \]

で求めることが出来ます．

斜面崩落モデルの導入

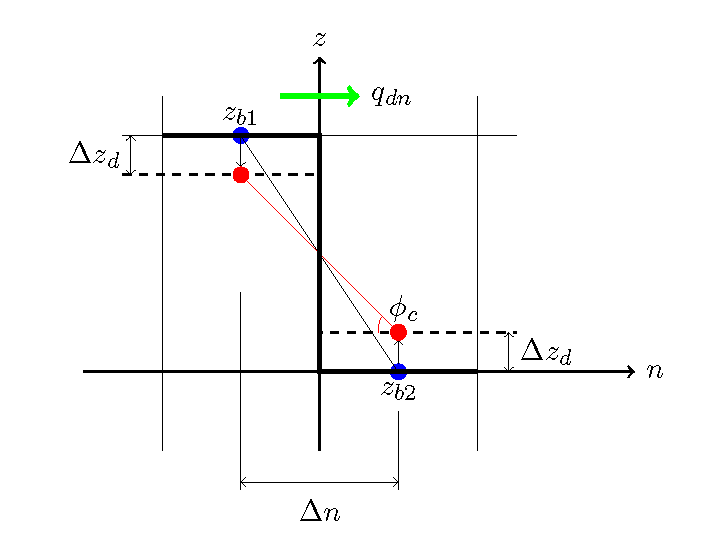
Figure 136 : 斜面崩落モデル

Figure 136 に示すように断面のある部分で隣り合う格子間の手負い面勾配が 安息角である \(\phi_c\) を超えた場合を考えてみます．この場合流砂量は無くても， 斜面の崩落が生じると考えると見かけ上の流砂が発生することになります． 今，隣り合う2点のそれぞれの河床高を \(z_{b1}, z_{b2}\) とし， 2点間の距離を \(\Delta n\) とすると，

(306)\[-\cfrac{\partial z_b}{\partial n} = \cfrac{z_{b1}-z_{b2}}{\Delta n} > \tan \phi_c\]

の時，流砂連続式の差分表示より,

(307)\[(q_{dn}-0)\Delta t=\Delta z_d \Delta n (1-\lambda)\]

ただし, \(q_{dn}\) は単位幅流砂量に換算した斜面崩落量Flux, \(\Delta t\) は数値計算上の時間刻み, \(\Delta z_d\) は斜面崩落によって低下する 斜面上方の地盤低下量(=斜面崩落によって上昇する斜面下方の地盤上昇量), \(\Delta n\) は対象とする2点間の距離, \(\lambda\) は空隙率です. 斜面崩落によって，2点間の斜面勾配は安息角まで緩くなる, 即ち, 地盤高さ変化後の 勾配が安息角となるので,

(308)\[\cfrac{(z_{b1}-\Delta z_d)-(z_{b2}+\Delta z_d)}{\Delta n}= \tan \phi_c\]

(307) と (308) より,

(309)\[q_{dn}=-\left( \cfrac{\partial z_b}{\partial n}+\tan \phi_c \right) \cfrac{(1-\lambda)}{2\Delta t} \Delta n^2\]

同様に,

(310)\[\cfrac{\partial z_b}{\partial n} = \cfrac{z_{b2}-z_{b1}}{\Delta n} > \tan \phi_c\]

の時は,

(311)\[q_{dn}=-\left( \cfrac{\partial z_b}{\partial n}-\tan \phi_c \right) \cfrac{(1-\lambda)}{2\Delta t} \Delta n^2\]

となります．これらを1本の式で書くと，

(312)\[\left|\cfrac{\partial z_b}{\partial n} \right| > \tan\phi_c \hspace{5mm} \mbox{のとき} \hspace{5mm} q_{dn}=-\left\{ \cfrac{\partial z_b}{\partial n} + \mbox{sign} \left(\cfrac{\partial z_b}{\partial n} \right) \tan \phi_c \right\} \cfrac{(1-\lambda)}{2\Delta t} \Delta n^2\]

となります． \(s\) 軸方向にも同様に，

(313)\[\left|\cfrac{\partial z_b}{\partial s} \right| > \tan\phi_c \hspace{5mm} \mbox{のとき} \hspace{5mm} q_{ds}=-\left\{ \cfrac{\partial z_b}{\partial s} + \mbox{sign} \left(\cfrac{\partial z_b}{\partial s} \right) \tan \phi_c \right\} \cfrac{(1-\lambda)}{2\Delta t} \Delta s^2\]

となります．ただし, \(q_{ds}\) は \(s\) 軸方向の斜面崩壊量を 流砂量に換算した値です. 斜面崩壊を考慮する場合は, (312) 式, (313) 式に よって得られる斜面崩壊量を (305) 式に付加することになります．

2次元河床の流砂連続式

\(s,n\) 座標(直交曲線座標)における流砂連続式は s-n座標における連続式の誘導(別解) で誘導した水の連続式 (447) の水のFlux部分を流砂量に置き換え, 空隙率を考慮することにより, 次式となります.

(314)\[\cfrac{\partial z_b}{\partial t} + \cfrac{1}{1-\lambda}\left( \cfrac{\partial q_{bs}}{\partial s}+ \cfrac{1}{r}\cfrac{\partial(r q_{bn})}{\partial n} \right)=0\]

ただし, \(q_{bs}, q_{bn}\) はそれぞれ \(s, n\) 方向の単位幅流砂量です. 河床高の時間変化は, (266) と同様に,

(315)\[ \begin{align}\begin{aligned}\cfrac{\partial z_b}{\partial t}A_x(i,j) = \cfrac{1}{1-\lambda} \left\{ q_{bs}(i-1,j)\Delta n(i-1,j)-q_{bs}(i,j)\Delta n(i,j) \right.\\\left. + q_{bn}(i,j-1)\Delta s(i,j-1)-q_{bn}(i,j)\Delta s(i,j) \right\}\end{aligned}\end{align} \]

2次元河床変動計算の手順

河床変動計算は以下の手順になります．

1. 計算格子の設定，初期河床高の設定

2. 格子に沿ったの曲率( \(1/r\) )の計算[ (262) 式]

3. 計算条件(境界条件・初期条件・水理量)の設定

4. 時間 \(t=0\)

5. [ 蛇行河川流れの計算(実践編) ]で示した計算法による流速・水深場の計算

6. 流線の曲率( \(1/r_s\) )の計算 [ (292) \(\sim\) (295) 式]

7. 河床せん断力および全流砂量の計算

8. 2次流の影響および斜面効果を考慮した \(s, n\) 方向流砂量の計算[ (305) 式]

9. 斜面崩落を考慮する場合は (313) 式で計算して, \(s, n\) 方向流砂量に加える

10. 河床変動計算[ (315) 式]

11. 時間の更新 \(t=t+\Delta t\)

12. 5. に戻って繰り返し計算(所定の時間まで繰り返す)

計算コードと計算結果

ここまでの説明に従って作成した2次元蛇行水路の流れと河床変動計算の計算コードは こちらです．

https://github.com/YasuShimizu/Nays2d_Bed_Deformation

このコードを用いて行った Figure 137 に示すの長谷川　[Ref:27] による移動床 実験(Me-2)の再現計算例を, Figure 138 に示します． 計算結果は実験結果を良好に再現 しているようです．

Figure 137 : 長谷川(1986) [Ref:27] による実験結果(Me-2)

Figure 138 : 長谷川(1986) [Ref:27] による実験(Me-2)の再現計算

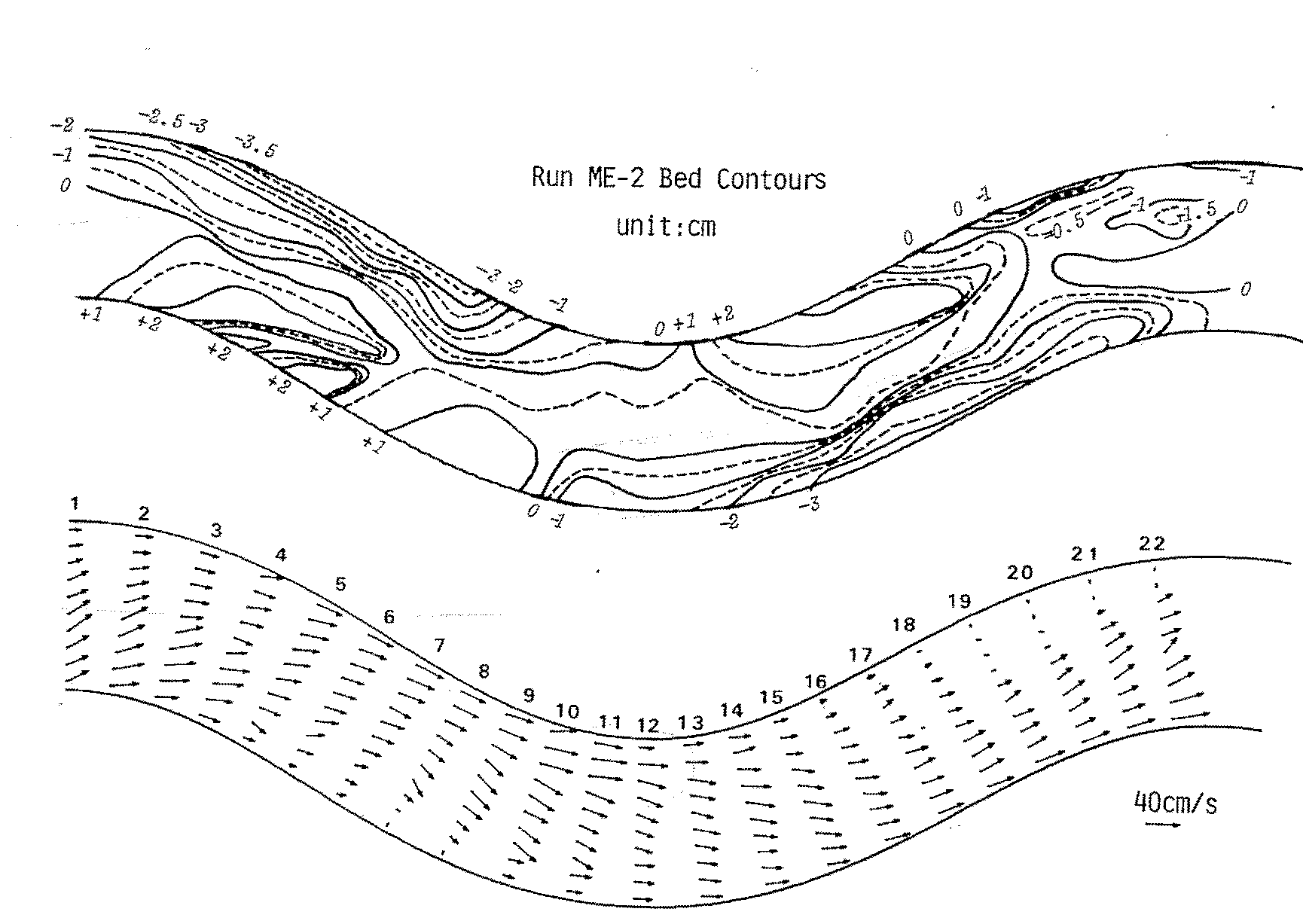
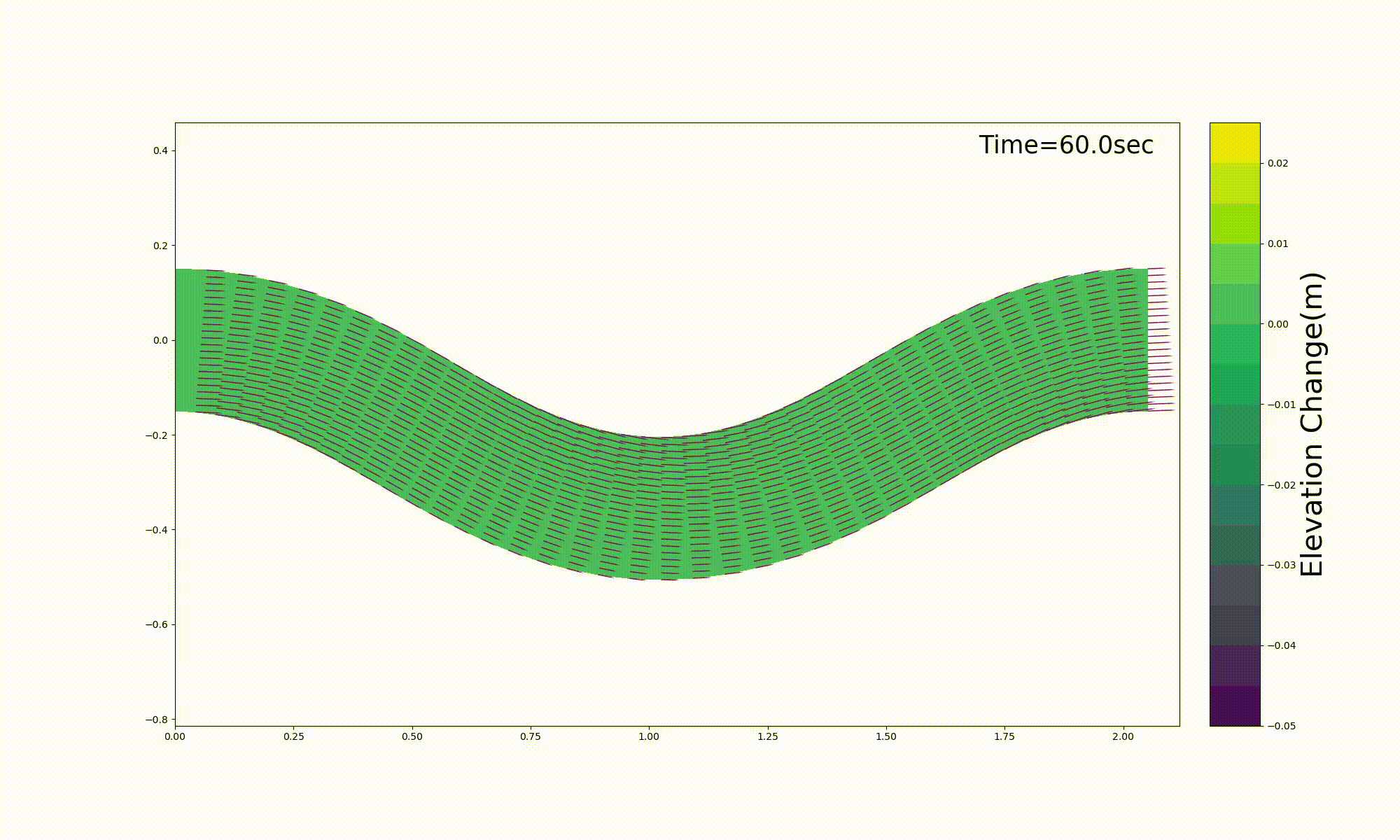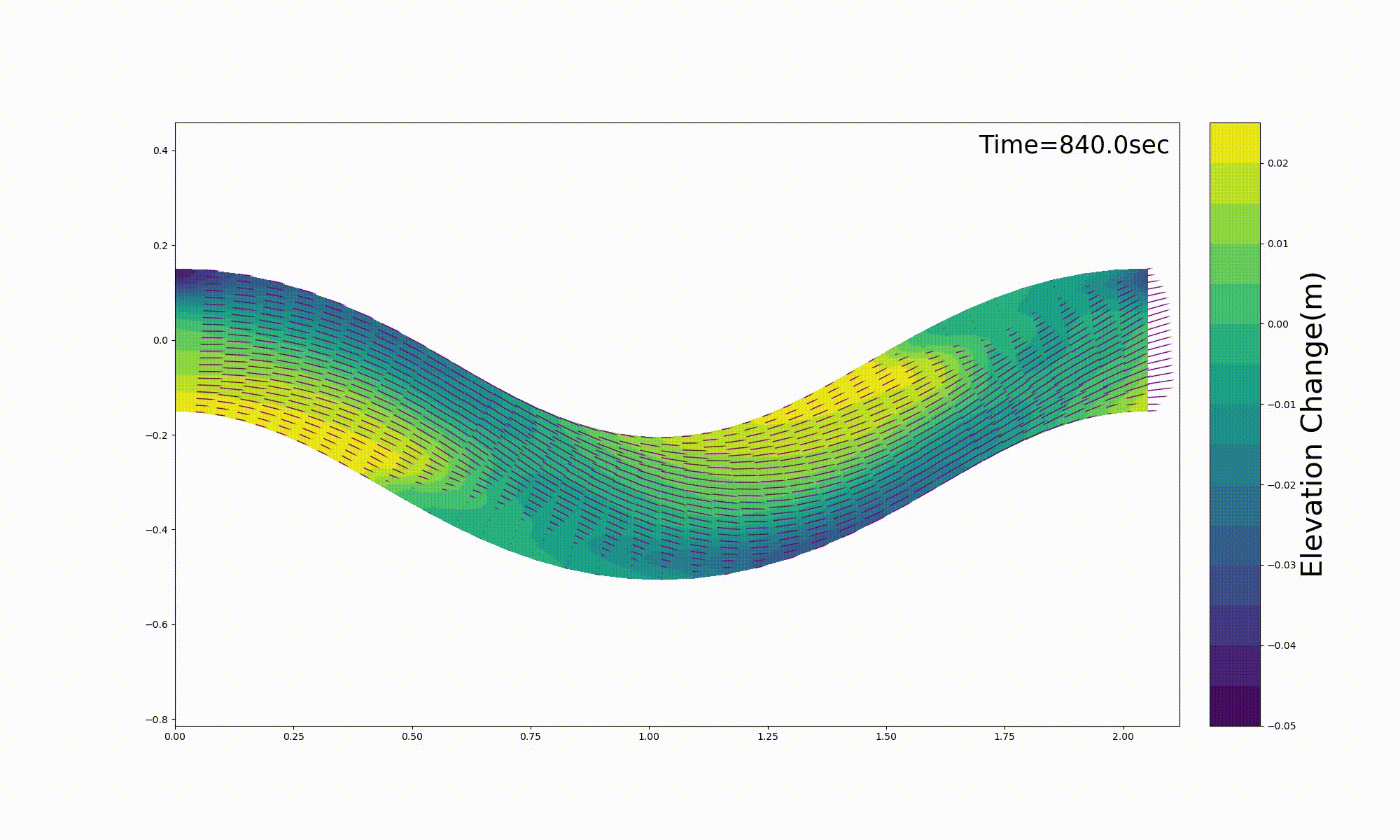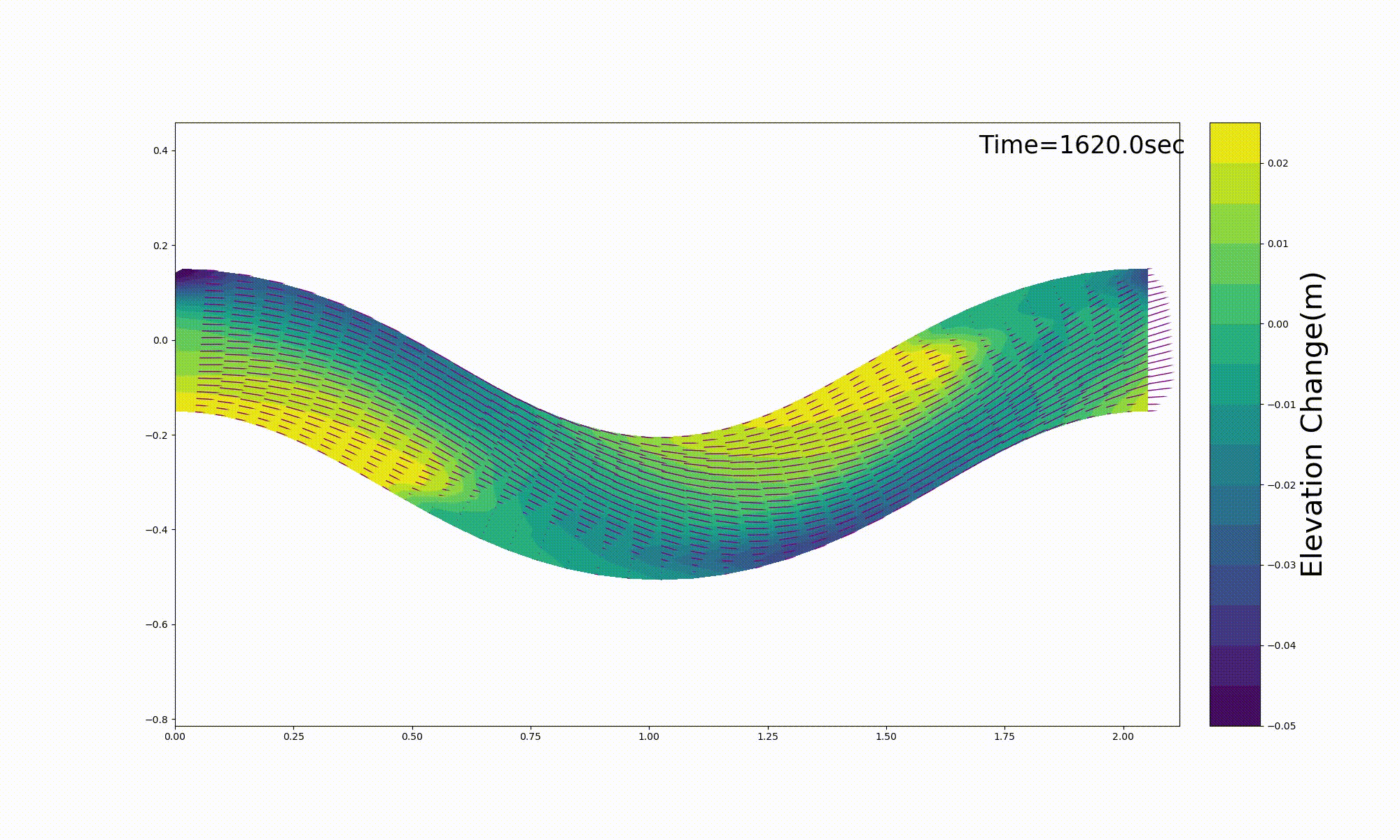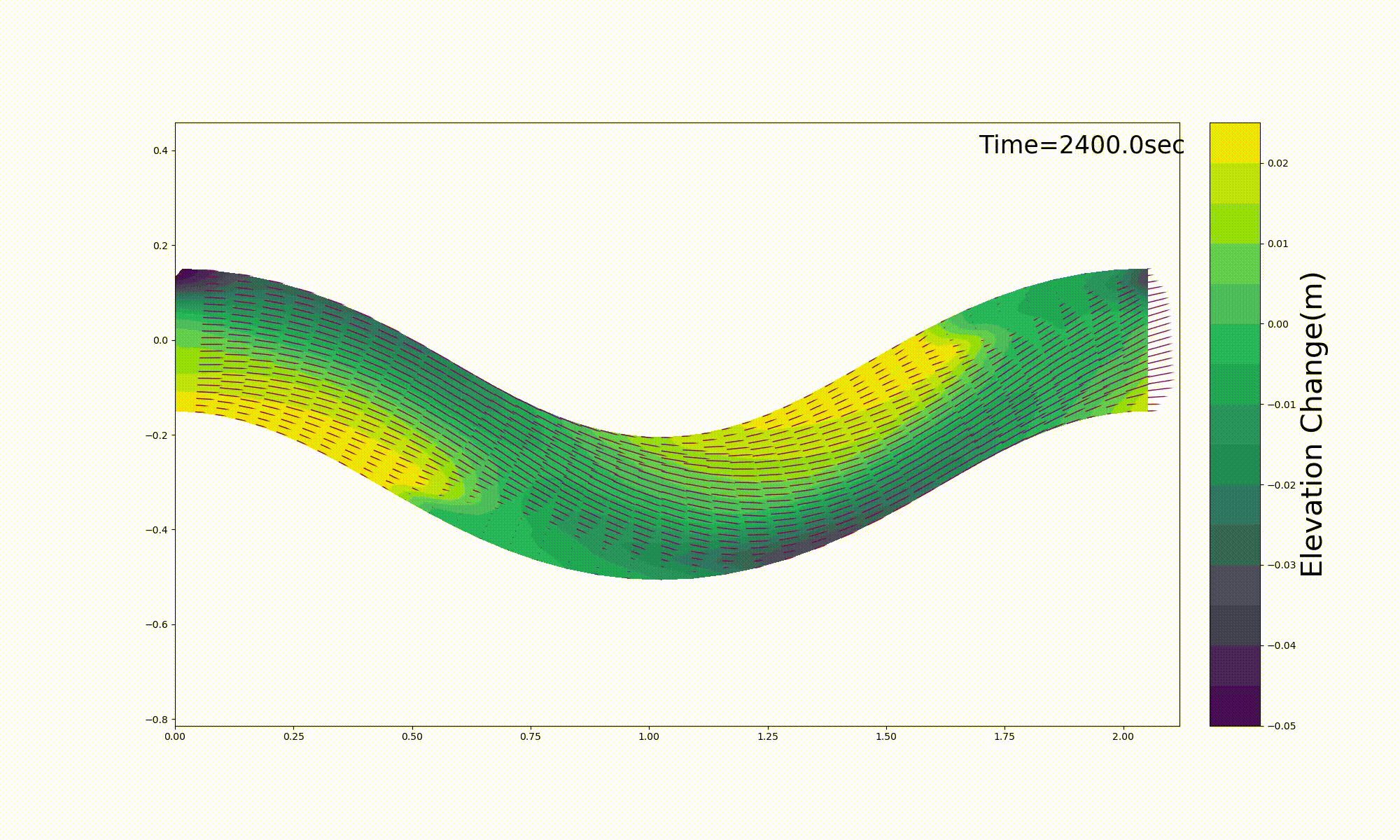
なお，Figure 138 の計算例で使用したパラメーターや計算条件は，すべて 上記ソースコードを公開しているGitHubのRepositoryにある, me-2.yml というymlファイルに記述させ，計算を実行すると，この条件を読み込んで 計算が行われます．

https://github.com/YasuShimizu/Nays2d_Bed_Deformation/blob/main/me-2.yml

パラメーター類の説明はすべて角項目の隣に記述されております． 本テキストでは全てのパラメーターについての説明はしませんでしたが， ソースコード本体と比較しながら見て頂くとその意味が分かると思います． 基本的に係数類はデフォルトの値で問題無いと思います． 説明が必要な場合は，こちらへお願いします. <https://i-ric.org/yasu/nbook2/bbs23/bbs23.cgi>`_

me-2.ymlの内容は以下となります.:

j_rep: 1 # 周期境界条件 0:周期境界条件無 1:周期境界条件

lam : 2.2 # 水路の波長(m)
nx0 : 41 # 格子数/1波長
ny : 21 # 横断方向格子数(奇数推奨)
wn : 1 # 波数
chb : 0.3 # 水路幅(m)
t0_degree : -30 # 最大蛇行偏角(Degree)
slope: 0.00333 # 水路勾配
xsize: 20 # 計算結果をプロットする図の横スケール


amp : 0.0 # 初期河床砂州の波高(m)
delta : 0. # 初期河床砂州の位相差(m)
beta_0: 0. # 内岸で川幅を狭める割合
amp_0: 0.0 # 狭めた部分の河床高さ(m)

snu_0 : 1e-6 # 動粘性係数
hmin : 0.0001 # 最小水深(m)
vmin : 0.0001 # 最小流速(m/s)
cw: 0.001 # 側壁摩擦係数
ep_alpha: 1. # 渦動粘性係数の係数

qp: 0.00187 # 流量(m^3/s)
snm: 0.021 # マニング粗度
g: 9.8 # 重力加速度(m/s^2)
diam: 0.00043 # 河床材料平均粒径(m)
slambda: 0.4 # 空隙率
musk: 0.1 # μs×μk 静止摩擦係数×動摩擦係数
nsta: 7.0 # 2次流強度

j_west: 0 # 上流条件(0:開放, 1:閉鎖)
j_east: 0 # 下流条件(0:開放, 1:閉鎖)
j_hdown: 1 # 下流端水位条件(0:自由流出, 1:等流水深, 2:固定水位を与える)
h_down : 1. # j_hdown=2 の時の固定水位(m)
j_inih: 2 #初期水位縦断 0:直線 1:等流計算 2:不等流計算

alh: 0.7 # 水位収束計算のReluxsation係数
lmax: 10 # 各タイムステップでの水位収束計算最大回数

etime: 2400. # 計算終了時間(sec)
tuk: 10. # 計算結果アウトプット間隔(sec)
dt: 0.002 # 計算タイムステップ(sec)
stime: 0. # アウトプット開始時間(sec)
bstime: 60. # 河床変動開始時間(sec)

j_obst: 0 # 障害物の有無 0=無 1=有
jo_type: 2 # 障害物設置方法 1=ファイルから読む 2=条件を指定する
jo_method: 4 # 0=無 1=右岸のみ 2=左岸のみ 3=左右岸(千鳥) 4=左右岸(同位置)
f_dike_pos: 0.8 # 最初の水制の位置(m)
dike_dis: 0.8 # 水制間隔(m)
dike_length: 0.1 # 水制長(m)
dike_thick: 0.02 # 水制厚(m)
num_dike : 3 # 水制本数(方岸当たり)

iskip: 1 # ベクトルプロットの i 方向間引き
jskip: 1 # ベクトルプロットの j 方向間引き
jscale: 10 # 流速ベクトルのスケールファクター

alpha_upu : 0.1 # 周期境界条件の緩和係数

vcolor : yellow # ベクトルのカラー
rrmax: 1 # 曲率プロットの軸最大値(1/m)

dz_min: -0.05 #河床変動コンタープロット最小値(m)
dz_max: 0.03 # 河床変動コンタープロット最大値(m)
dz_step: 0.005 #上記コンターのステップ

メインのコードはmain.pyで，これを実行すると他の関数(Pythonではサブルーチンと呼ばずにすべて 関数と呼ばれるらしいです．機能はサブルーチンですが．．．)が呼び出されて 格子の形成，流れの計算，河床変動の計算，各種の作図，アニメーションの作成が行われます． なお，[png] [ping_q] [ping_r] [sed] [bed] というフォルダに時間毎の各種プロットが描きだされ ますので，これらのフォルダは予め用意しておいて下さい．

計算開始後，以下の図が作成される図が．

1. [ini_contour.png] 初期河床高コンター図(デフォルトでは平坦)

2. [curvature.png] 流路中心線に沿った計算格子座標の曲率縦断図

3. [longitudinal_prof.png] 初期河床と初期水面形の縦断図

4. [grid.png] 計算格子の平面図

この後計算が開始され，yml ファイルで指定された[tuk 計算結果アウトプット間隔(sec)] 毎に

1. [png] フォルダに水深コンターおよび平均流速ベクトル図のpngファイル

2. [ping_q] フォルダに流量，水路中心の水深平均流速，水路中心，左岸近傍，右岸近傍に沿った河床と水位の縦断図

3. [ping_r] フォルダに水路中心に沿った計算格子および流線の曲率，左右岸近傍の流線の曲率の縦断分布

4. [sed] フォリダに掃流砂量ベクトル図

5. [bed] フォルダに河床変動高(初期河床からの変動量)コンター図および水深流速ベクトル図

が作成されます． すべての計算が終了後に，上記角フォルダに作成された出力時間毎の静止画を用いて， gifよよびmp4形式の以下のアニメーションが作成されます．

1. [vec.gif] [vec.mp4] 水深コンターおよび平均流速ベクトル図の時間変化アニメーション

2. [longi.gif] [longi.mp4] 流量，流速，水路中心，河床と水位の縦断図のアニメーション

3. [radius.gif] [radius.mp4 格子および流線の曲率のアニメーション

4. [sed.gif] [sed.mp4] 流砂量ベクトルのアニメーション

5. [bed.gif] [bed.mp4河床変動高コンター図および水深流速ベクトルのアニメーション

Figure 138 に表示した河床変動の計算結果は，上記の [bed.gif] をそのまま貼り付けたものです．