この節の作者: 清水康行 <yasu@i-ric.org>

1次元河床変動計算

掃流砂のみの場合

1次元流砂連続式(掃流砂)

長方形断面水路における1次元流砂連続式を示します．

(236)\[ \cfrac{\partial z_b}{\partial t}+\cfrac{1}{(1-\lambda)B} \cfrac{\partial(B q_b)}{\partial x}=0\]

ただし, \(B\) は水路幅, \(\lambda\) は河床材料の空隙率です．

(236)　式の概念を Figure 84 に示します．図のように \(\Delta x\) 離れた2断面で流砂の 収支を考え，この差が \(\Delta t\) 時間継続した結果, 河床高が \(\Delta z_b\) 変化するとしたものです． 空隙率の考え方は, 流砂量の収支によって生ずる河床変動量の体積は，空隙 \(\lambda\) も含んで堆積(浸食)する ことを考慮したものです．

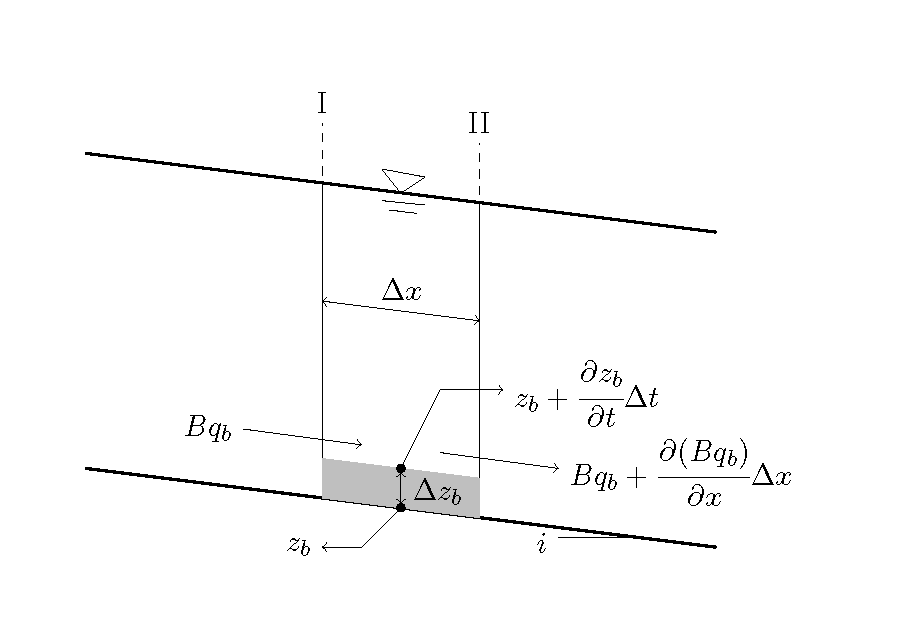
Figure 84 : 1次元河床変動概念図(掃流砂)

Figure 85 : スタカード格子(1次元河床変動計算)

掃流砂量に関する計算格子を Figure 85 のように配置した場合の (236) 式の差分表示は次式のように なります．なお，ここでの \(q_b\) の計算点は Figure 33 の \(u\) の計算点, \(z_b\) の計算点は Figure 33 の \(h\) の 計算点と同じです.

(237)\[z_b(i)^{n+1}=z_b(i)^n-\cfrac{\Delta t}{(1-\lambda)B(i)\Delta x} \left\{q_b(i)B_u(i)-q_b(i-1)B_u(i-1)\right\}\]

なお, \(B_u\) は \(q_b\) の計算点における \(B\) の値です. また, q_b(i)は各計算点において, (219) 式や (220) 式で求め, これら流砂量式で使用される \(\tau_\ast\) は (207) 式で求めます． ここで, (207) 式で使用される \(I_e\) はマニング式を用いる場合は,

(238)\[I_e= \cfrac{{n_m}^2 u^2}{h^{4/3}}\]

で求められます．

計算手順

計算手順は, Figure 35 の最後に (237) 式の河床変動計算を 追加した以下のフローとなります.

Figure 86 : 1次元河床変動計算フローチャート

Pythonコード

上記計算手順に沿ったPythonコードはこちらです．

https://github.com/YasuShimizu/1D_Flow_and_Bed_Deformation

計算の本体部分はこのレポジトリ内のmain.pyで，ここからこのレポジトリ内に記載された各々の 関数.py が呼び出されるようになっています． 計算条件は同じレポジトリ内のymlファイルで指定するようになっており下記４つの計算条件ファイルが含まれています．

1. 縦断方向中央部のマウンドがある河川の河床変動 : config_mound.yml

2. 縦断方向中央部に狭窄部がある河川の河床変動 : config_constriction.yml

3. 途中で勾配変化点を含む河川の河床変動: config_slope_change.yml

4. 上流から流砂の供給が無い河川（ダム下流）の河床変動: downstream_dam.yml

計算の実行は，例えば上記 1. の計算を実施したい場合はMinicondaのプロンプトで，

> python main.py config_mound

と，引数でファイル名の config_xxxxx.yml でxxxxの部分を指定してやると， その条件が記述されたymlファイルが呼び出されて実行されるようになっております．

計算結果

上記の4通りの条件による1次元河床変動計算結果を以下に示します．

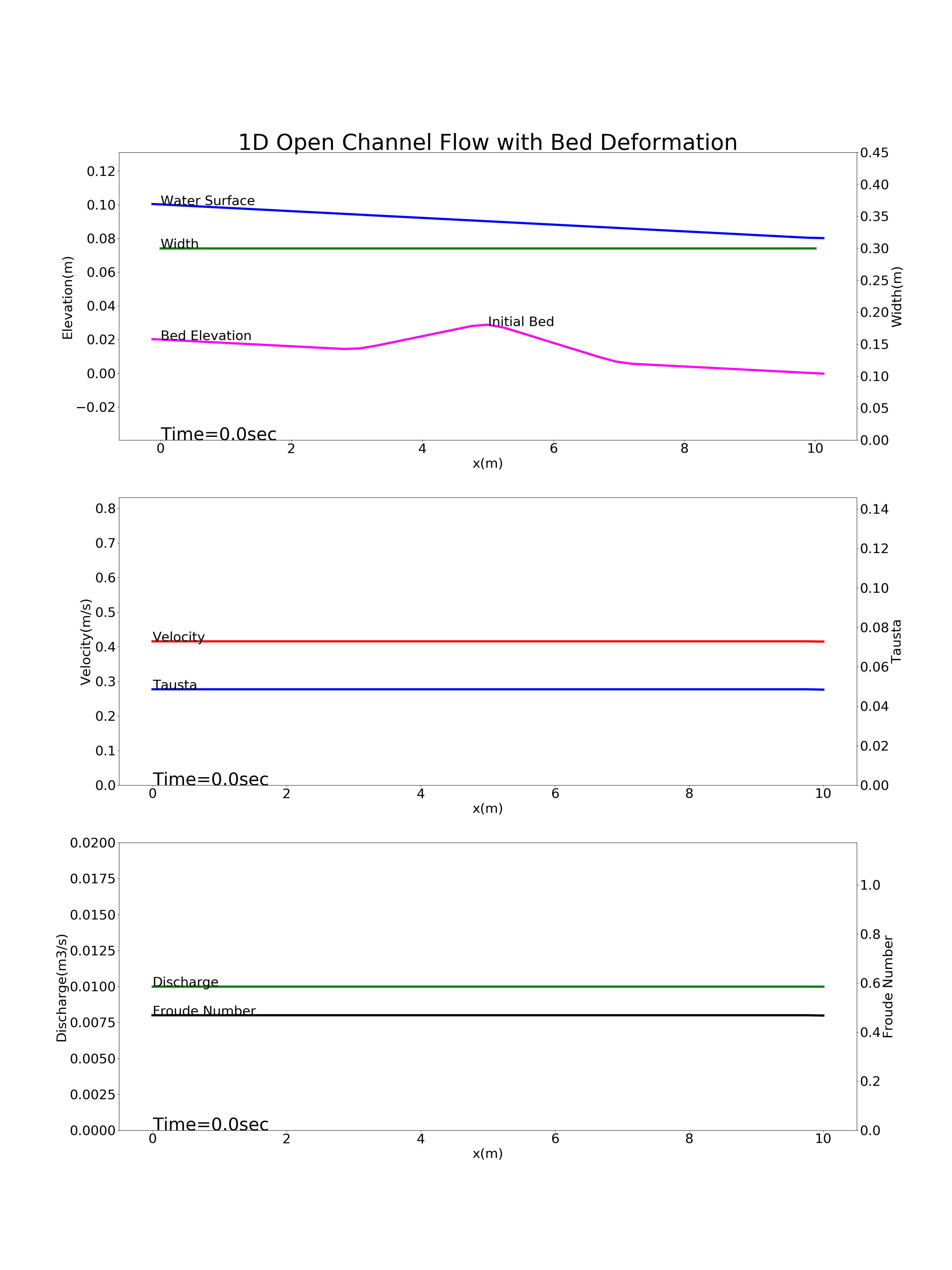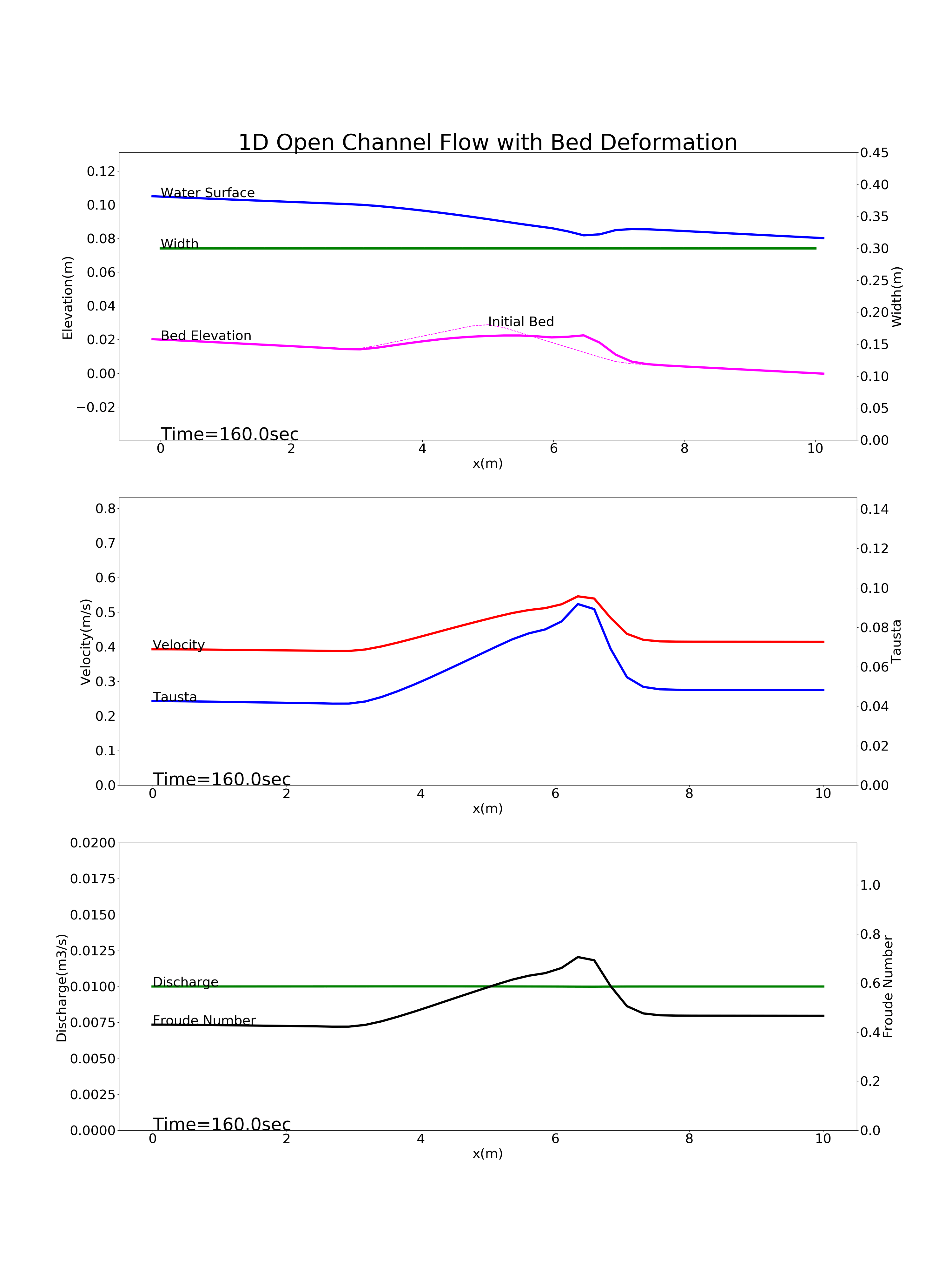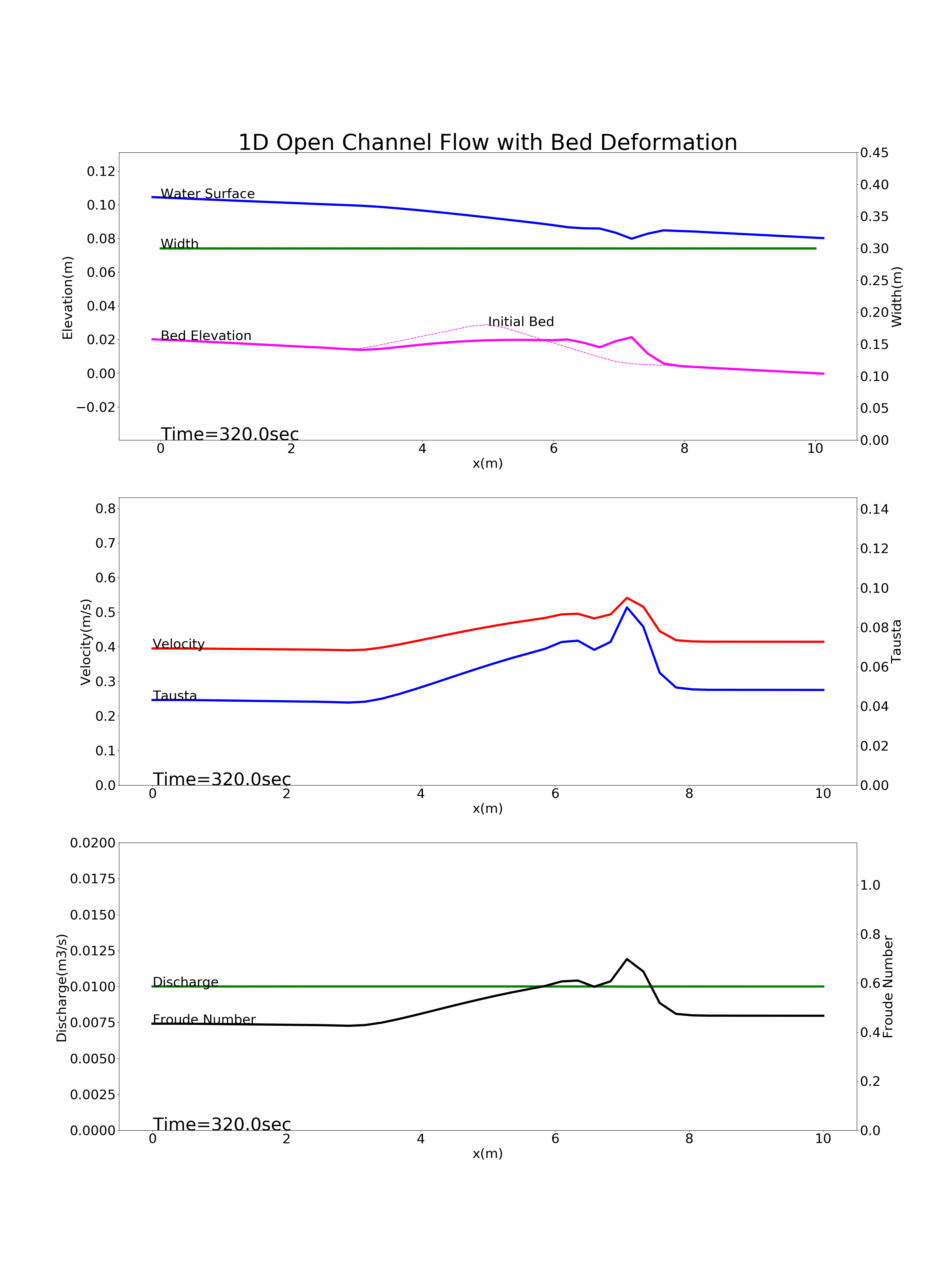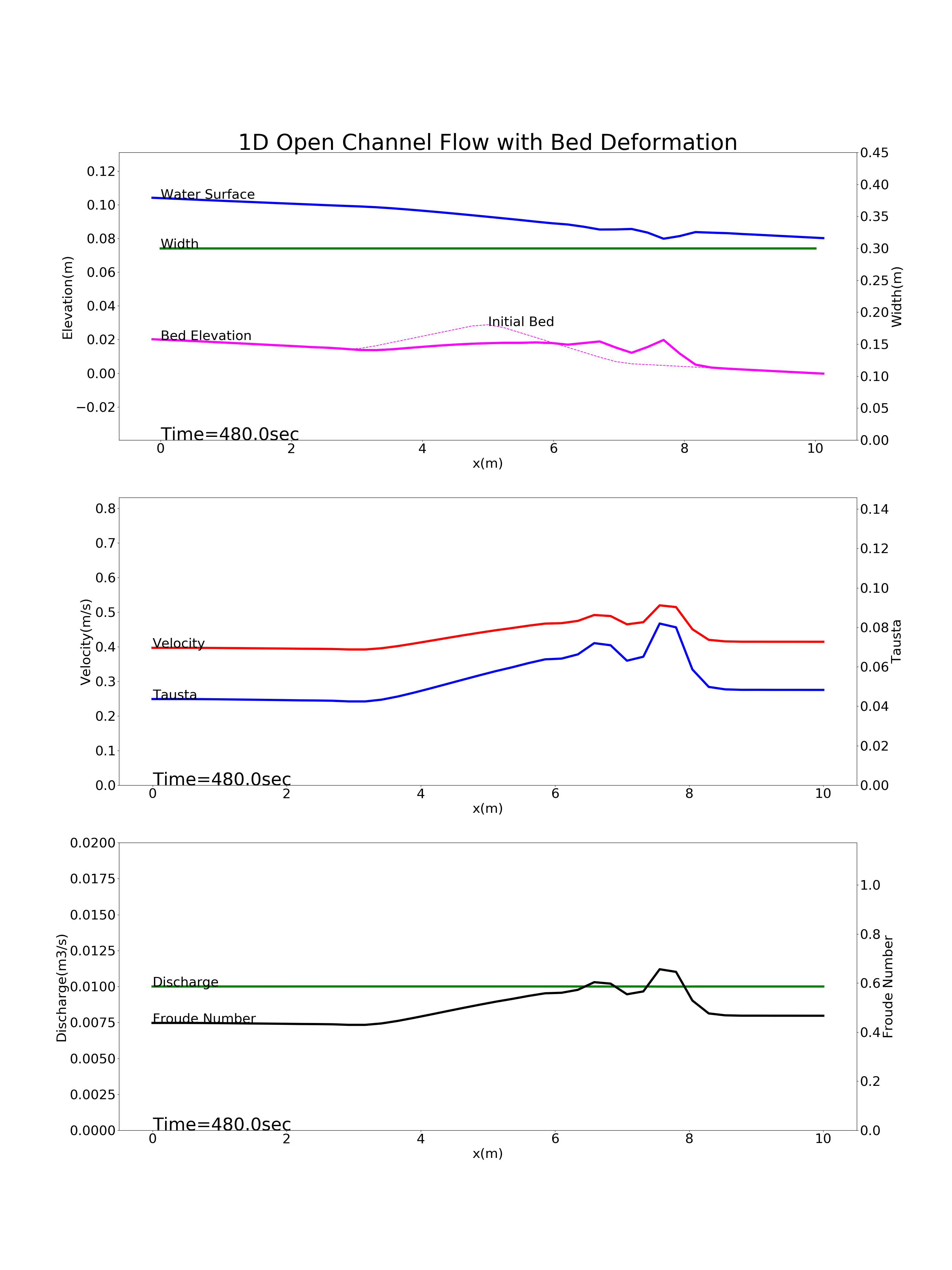
Figure 87 : 縦断方向中央部のマウンドがある河川の河床変動計算結果

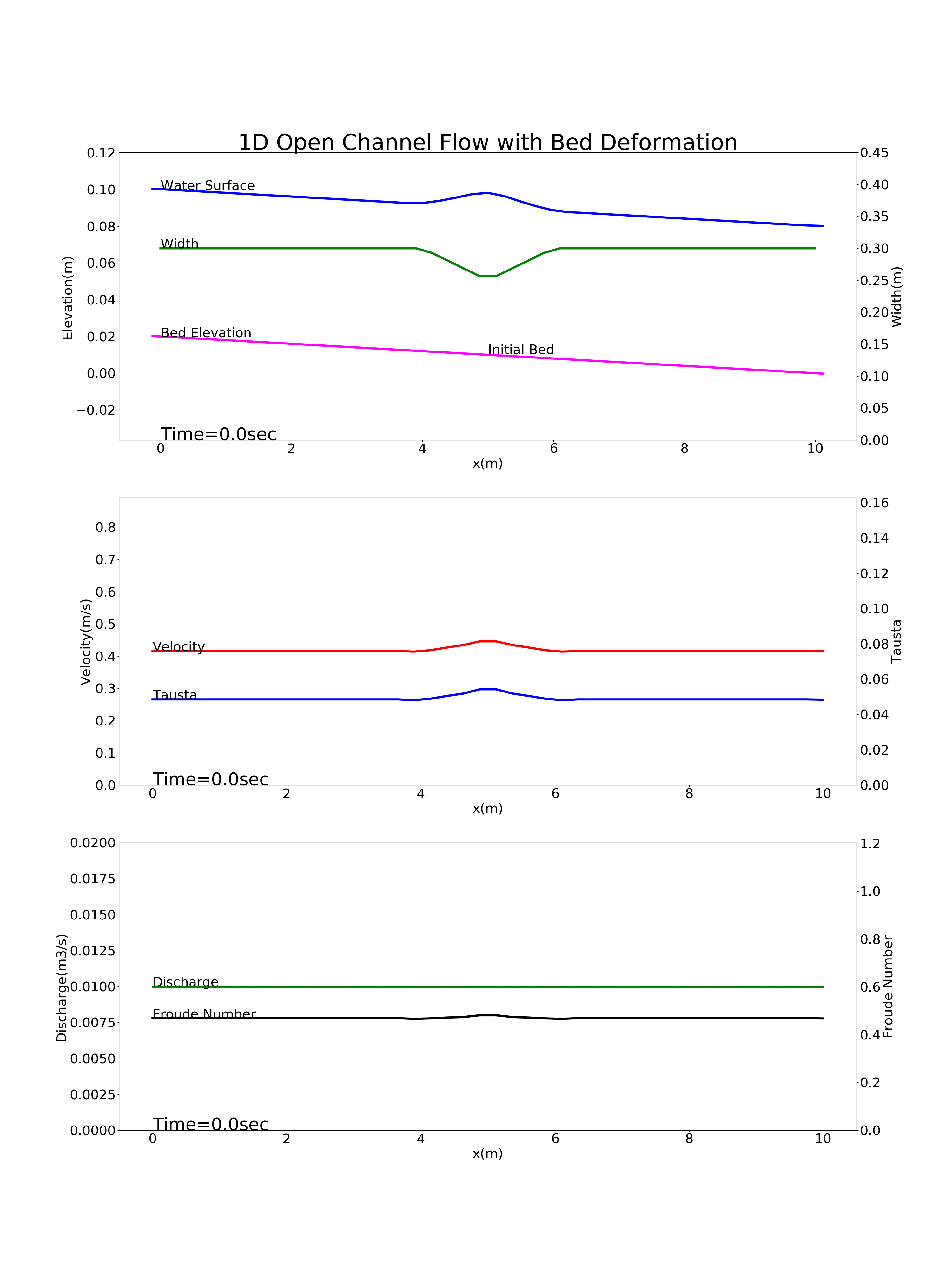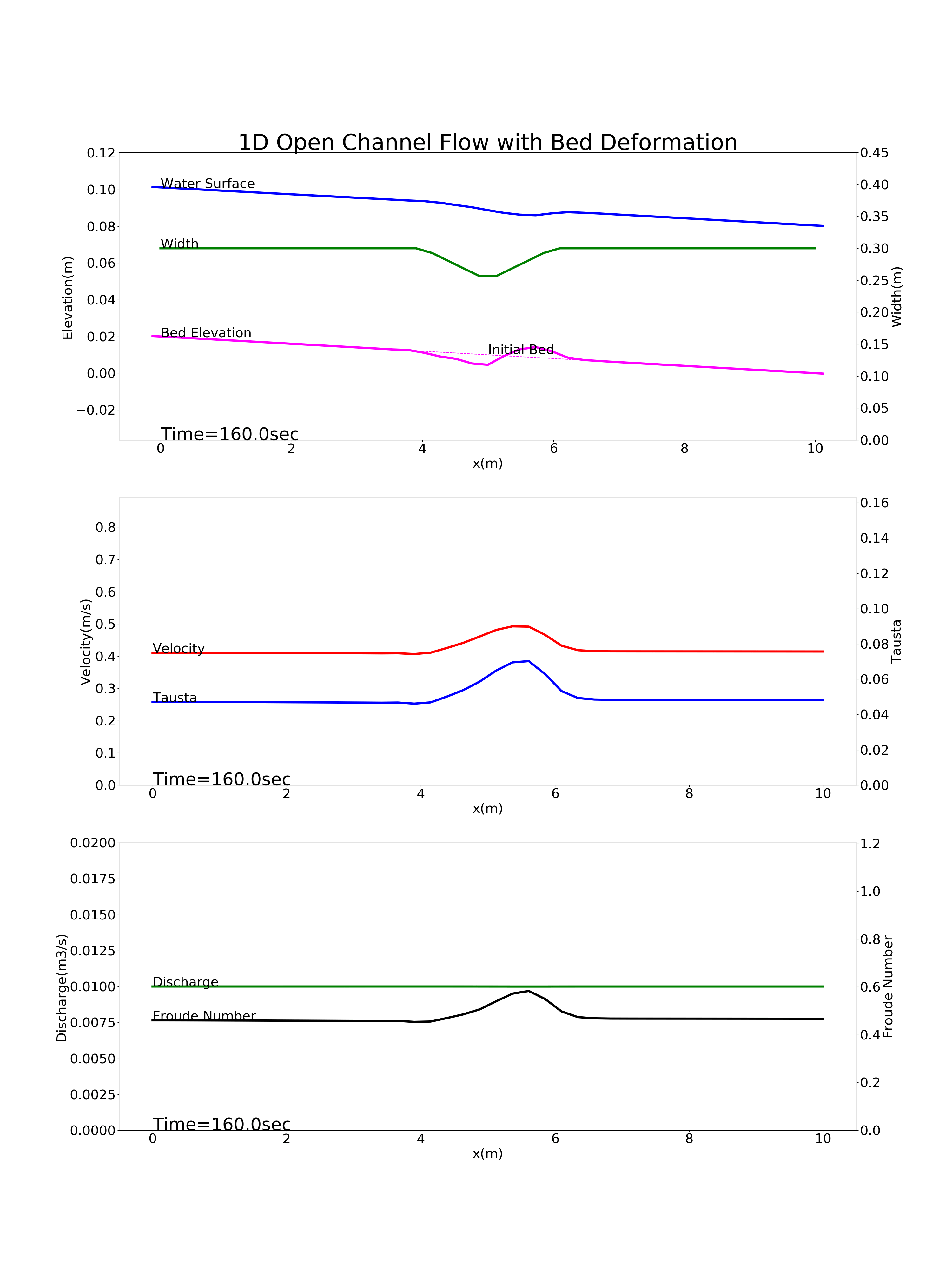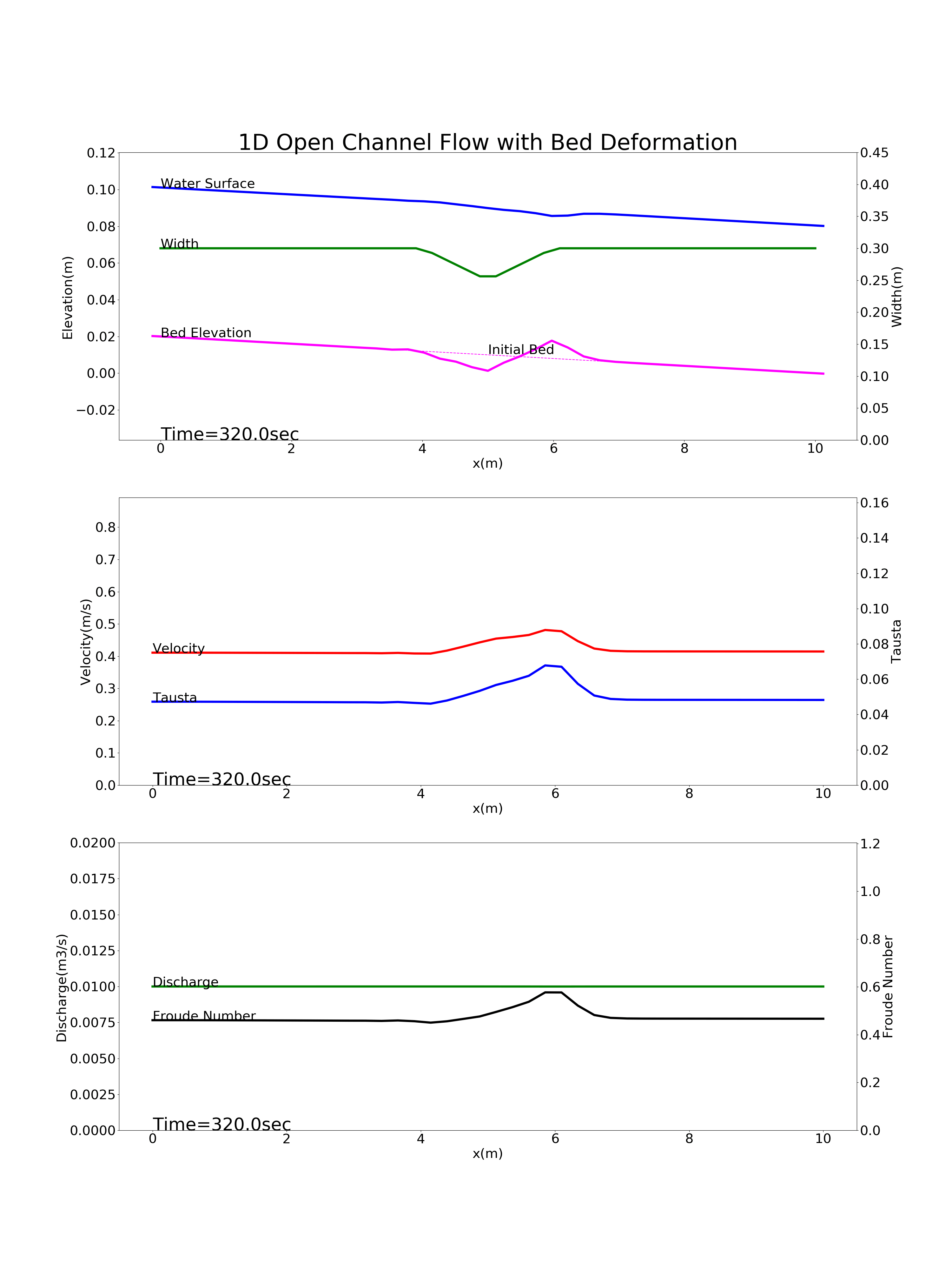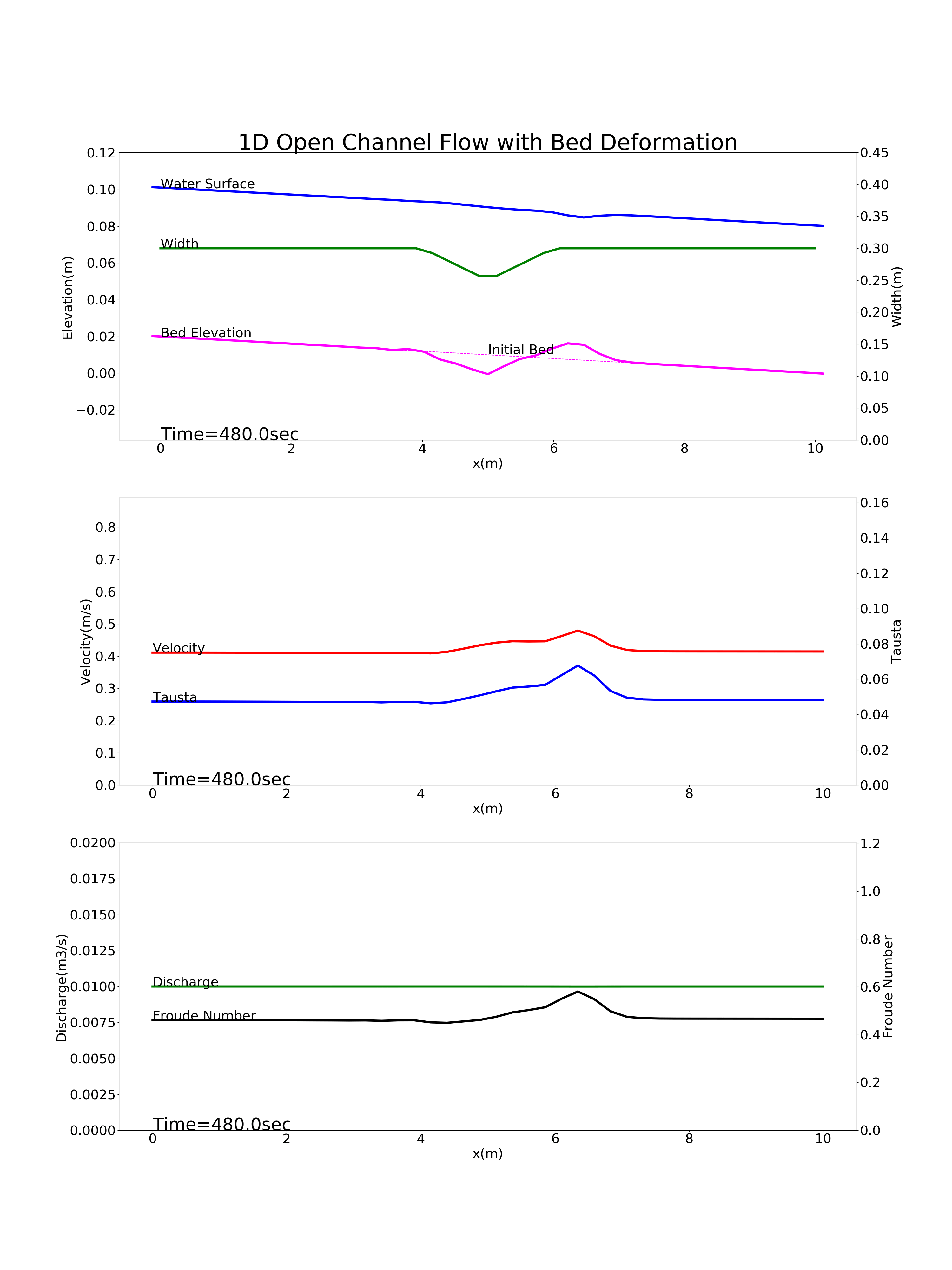
Figure 88 : 縦断方向中央部に狭窄部がある河川の河床変動計算結果

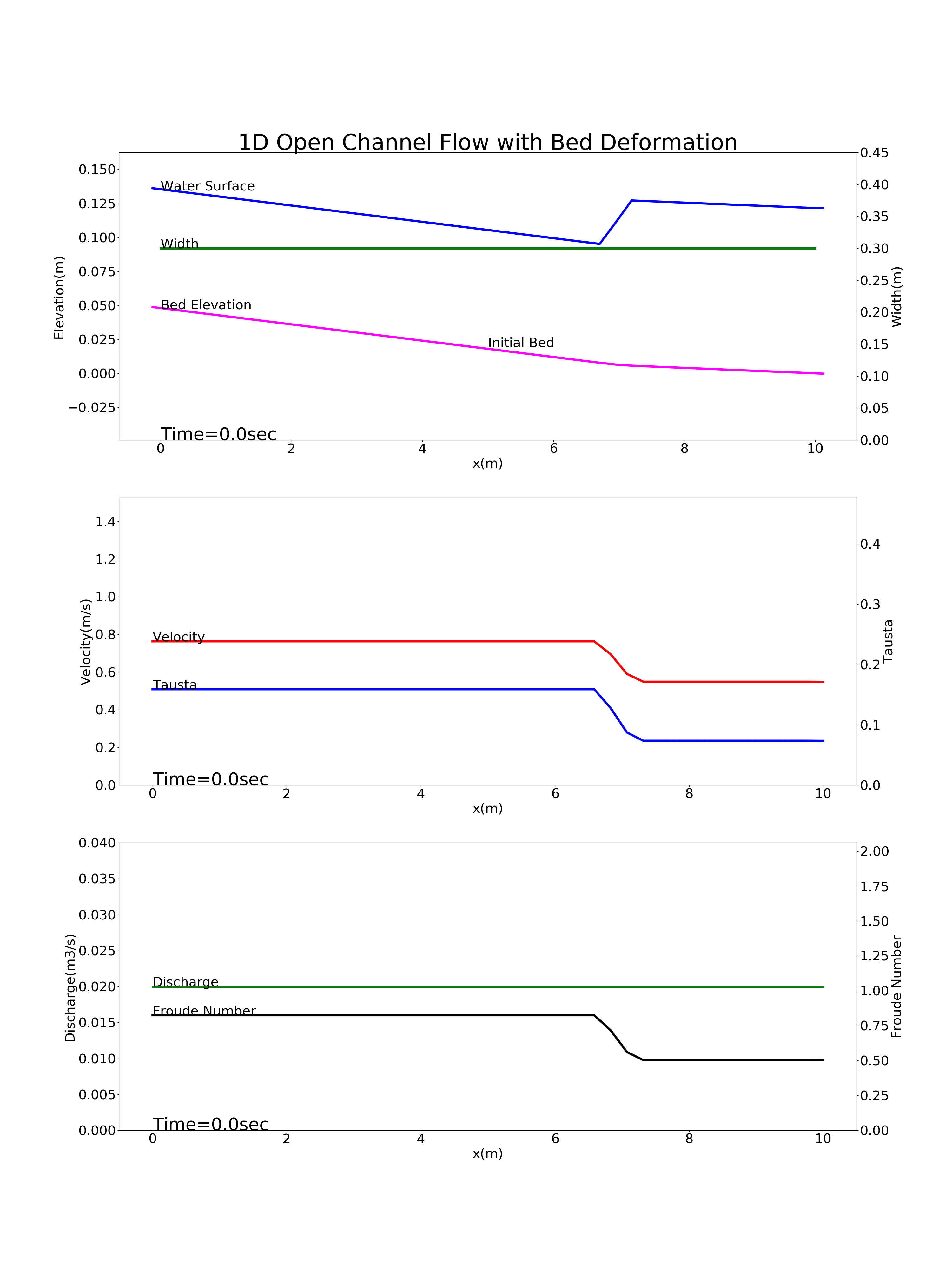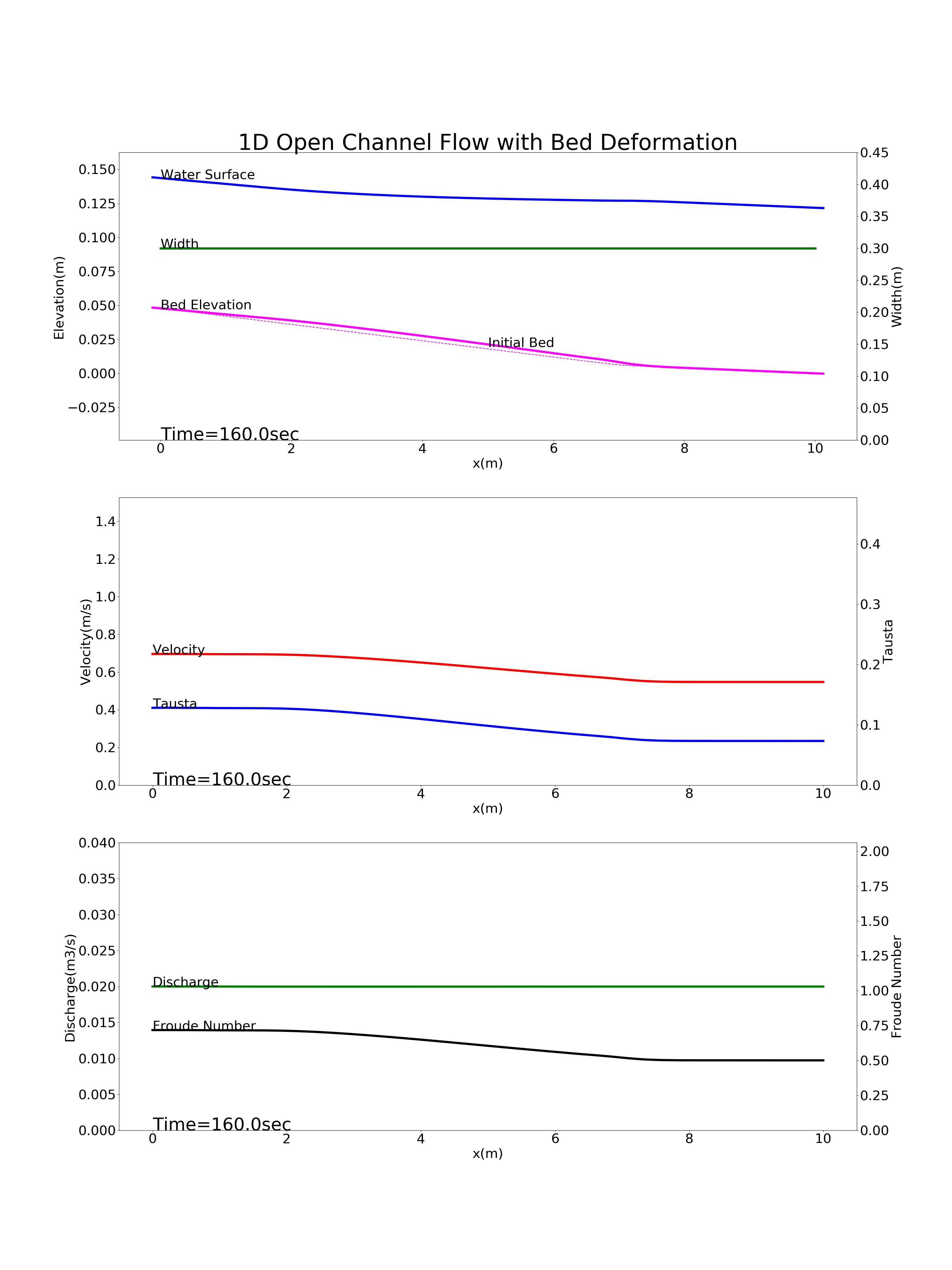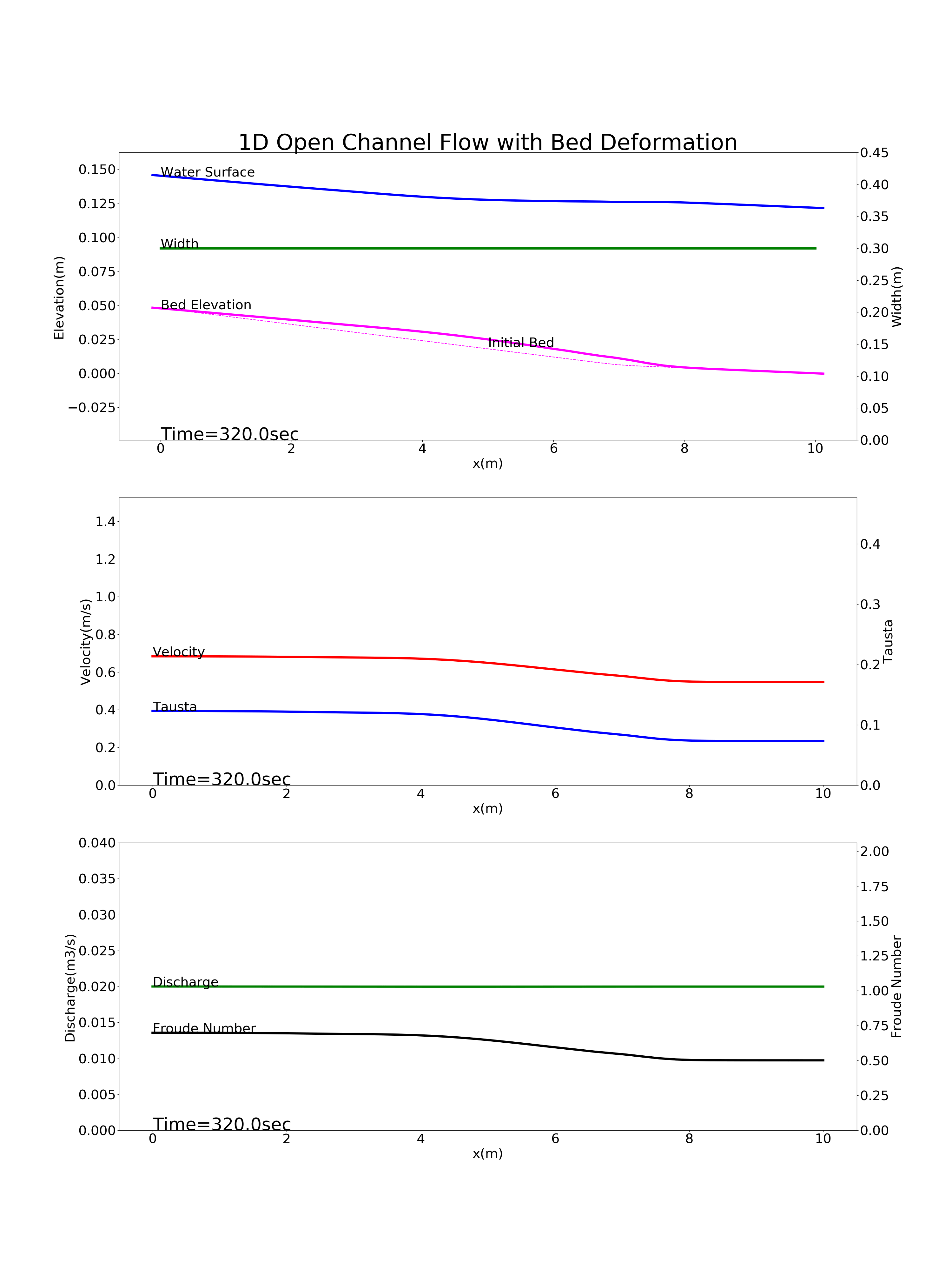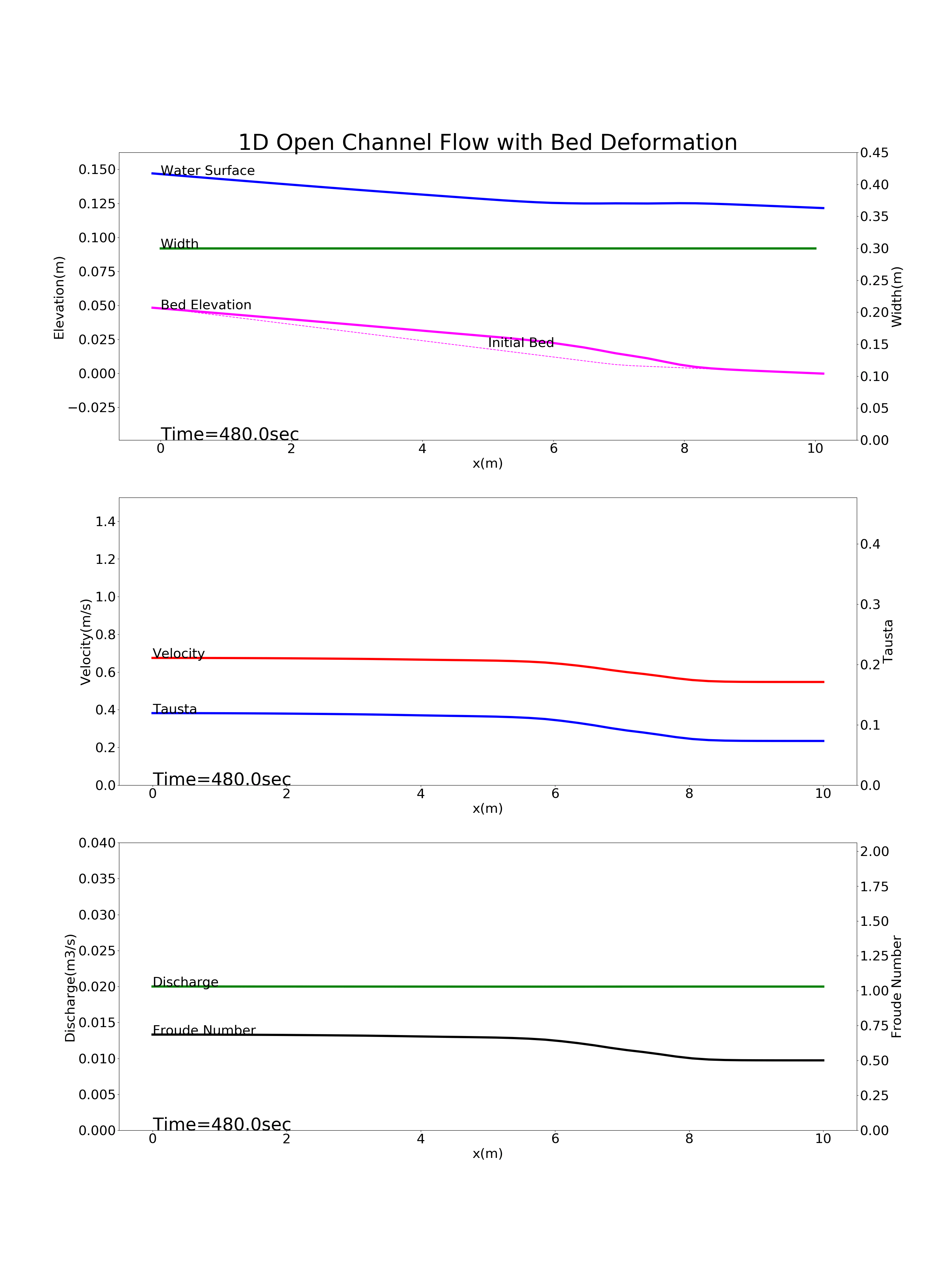
Figure 89 : 途中で勾配変化点を含む河川の河床変動計算結果

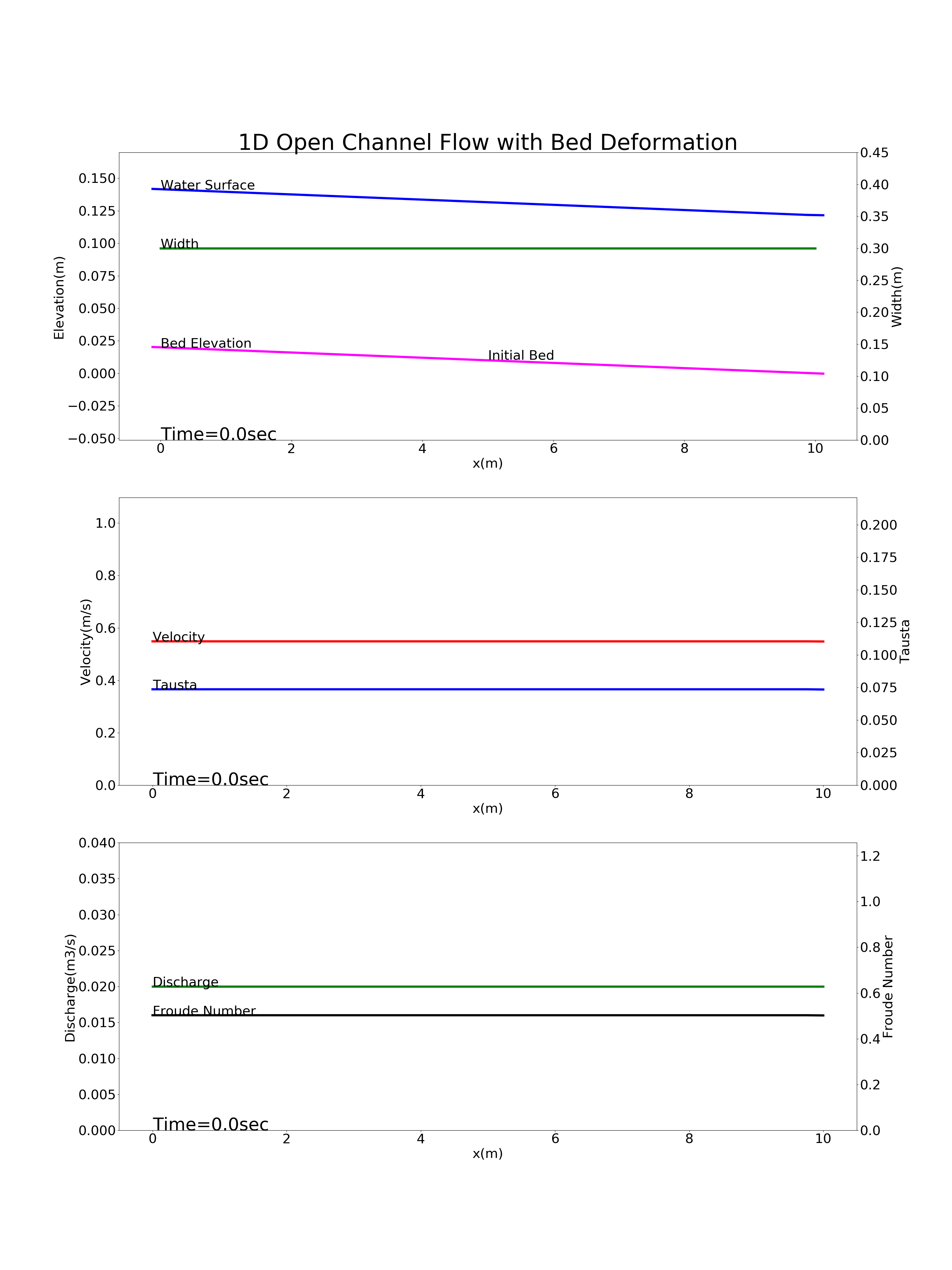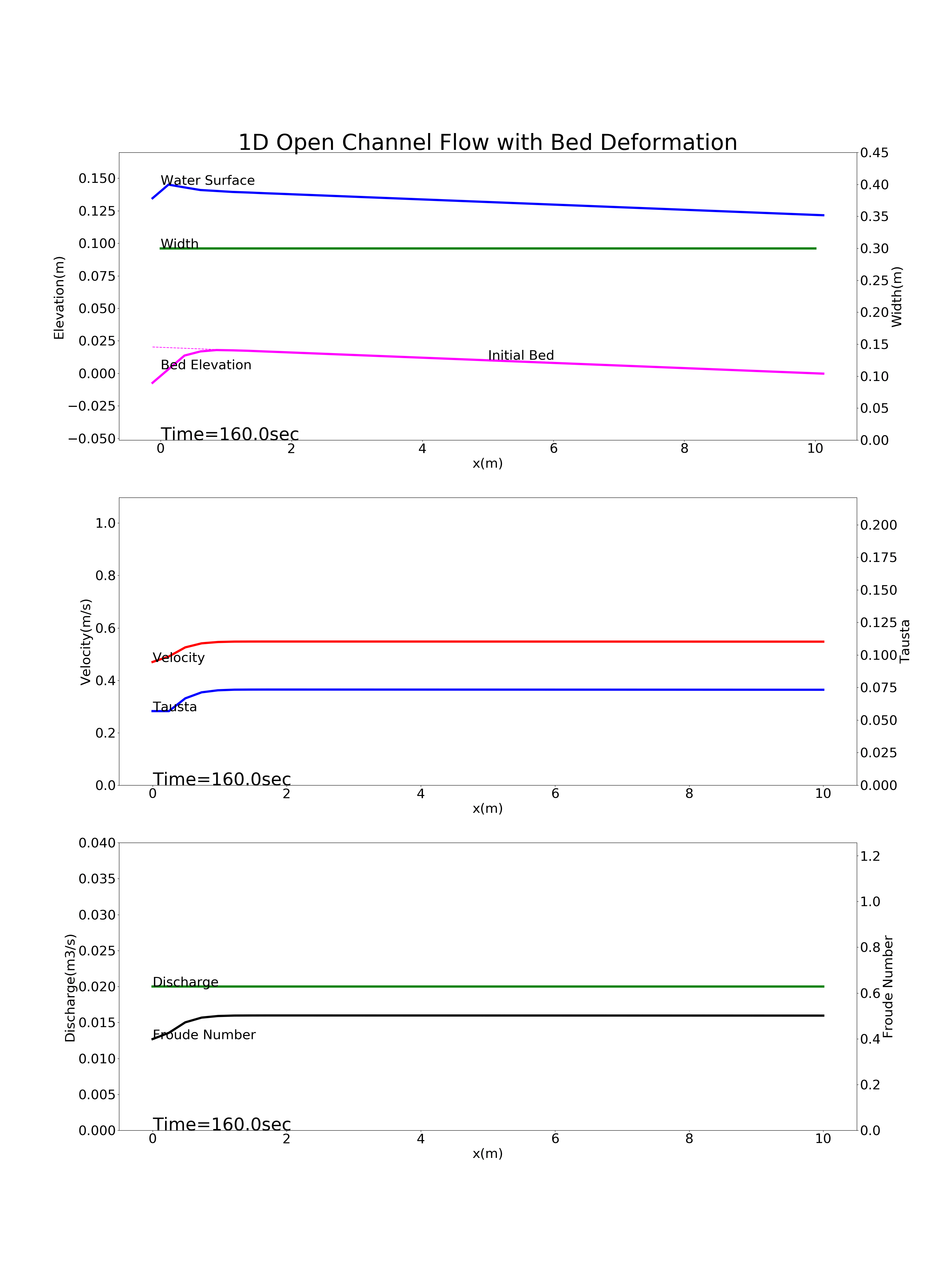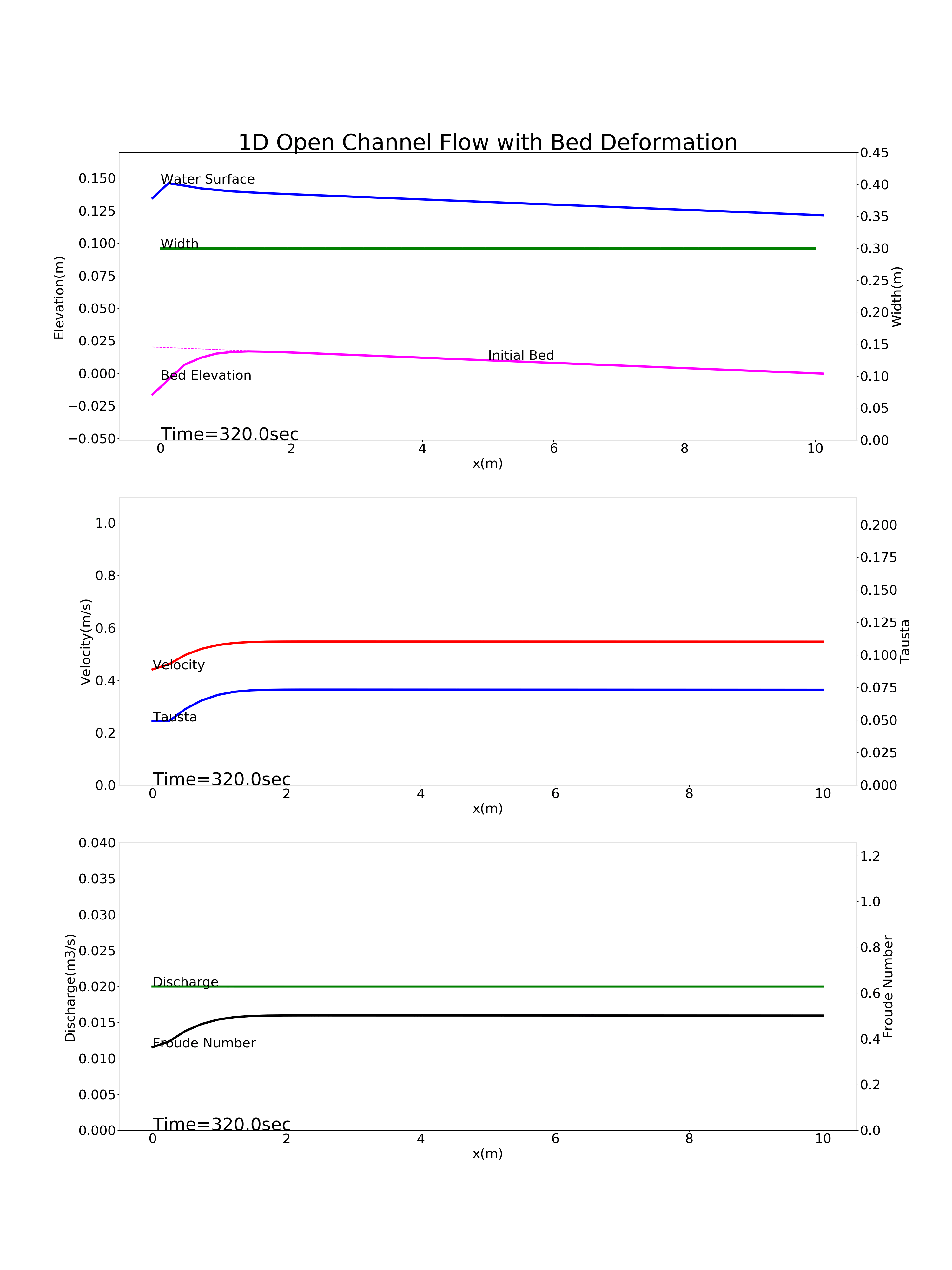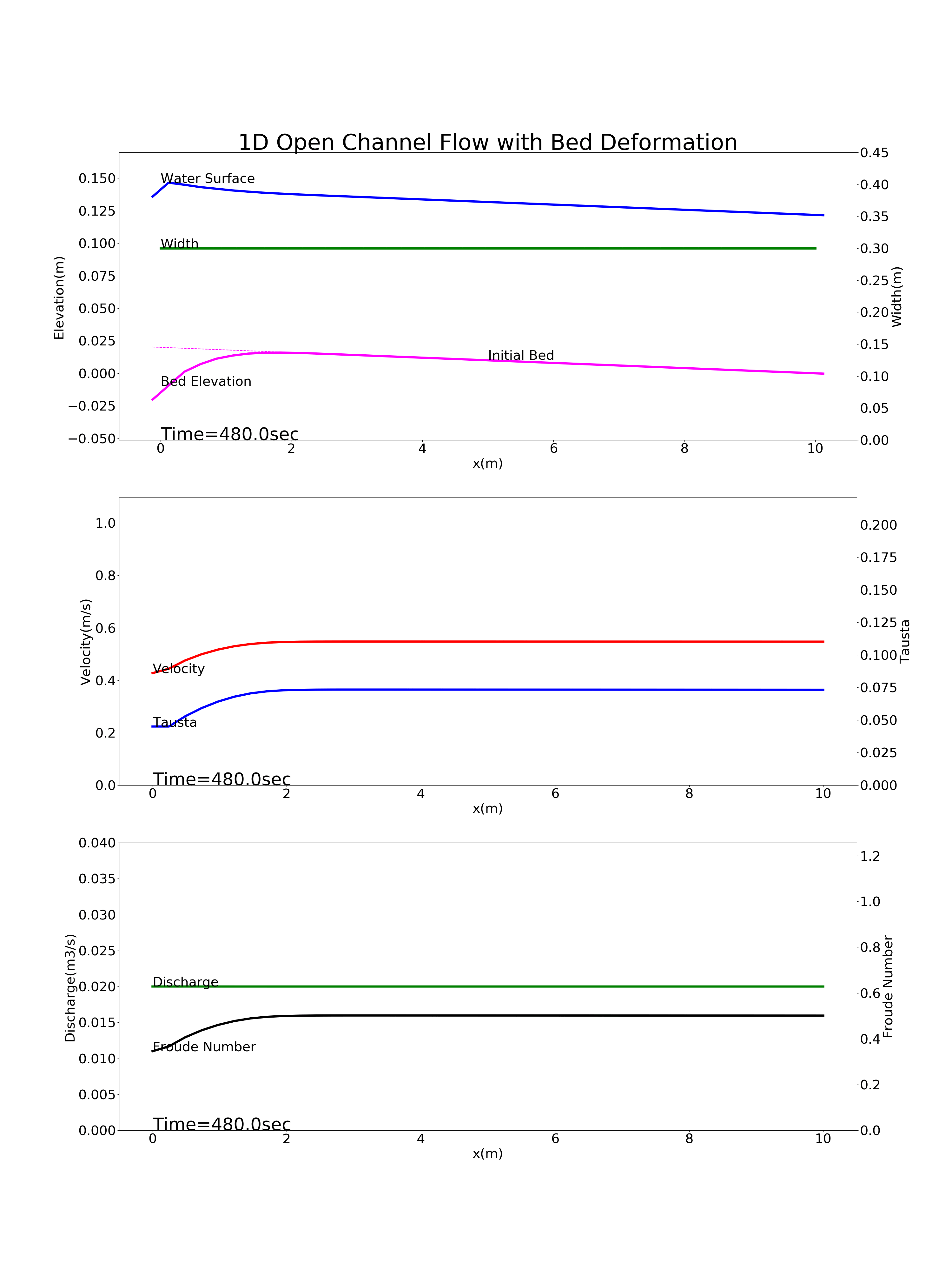
Figure 90 : 上流から流砂の供給が無い河川（ダム下流）の河床変動計算結果

浮遊砂による河床変動

1次元浮遊砂濃度の連続式

Figure 91 に示すように，長方形断面流路中に間隔が \(\Delta x\) のI, II断面を考え， 浮遊砂の連続条件を考えます.

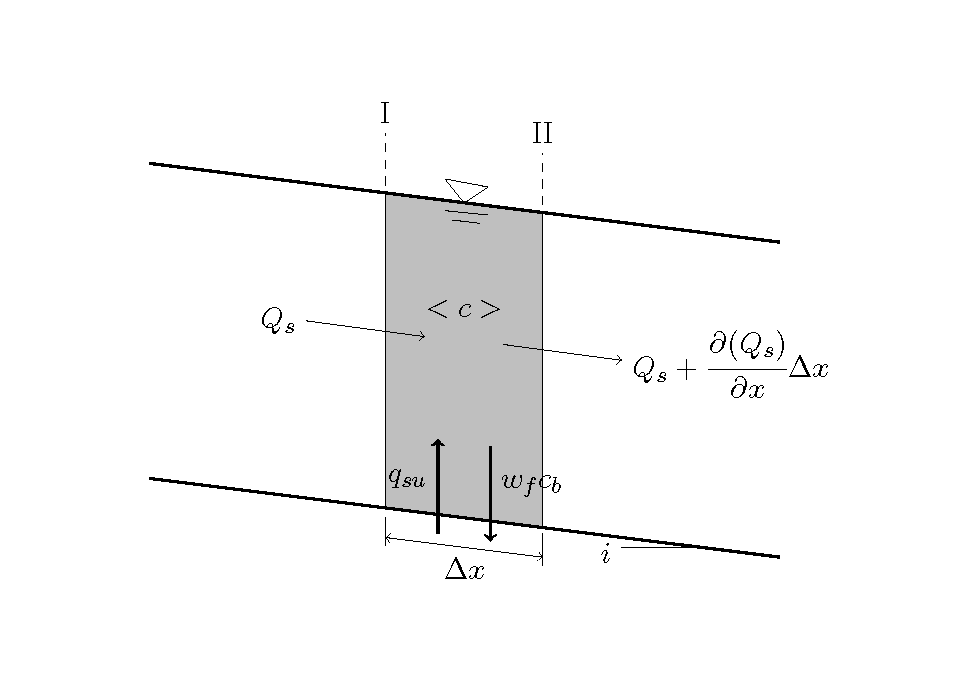
Figure 91 : 1次元浮遊砂の連続条件概念図

上記 \(\Delta x\) 区間の見ずの体積を \(V\), 平均濃度を \(<c>\), 平均水深を \(h\), 区間内の平均水路幅を \(B\) ,通過する浮遊砂量を \(Q_s\) とすると，

(239)\[\cfrac{\partial(V<c>)}{\partial t} \Delta t + \cfrac{\partial{Q_s}}{\partial x} \Delta x \Delta t =(q_{su}-w_f c_b) \Delta x \Delta t B\]

ただし, \(q_su\) は単位面積単位時間当たりの河床からの浮遊砂浮上量, \(w_f\) は沈降速度, \(c_b\) は河床における浮遊砂濃度です． また,

(240)\[V=A\Delta x = BH \Delta x, \; \; \; Q_s=Q<c>=Bhu<c>\]

なので，

(241)\[\begin{split}\cfrac{\partial(V<c>)}{\partial t}=B \Delta x \cfrac{\partial}{\partial t} (h<c>) \\ \cfrac{\partial Q_S}{\partial x}=\cfrac{\partial}{\partial x}(Bhu<c>)\end{split}\]

よって, (239) 式は

(242)\[\cfrac{\partial(h<c>)}{\partial t} B \cancel{\Delta x \Delta t} + \cfrac{\partial(Bhu<c>)}{\partial x} \cancel{\Delta x \Delta t} = (q_{su}-w_f c_b) B \cancel{\Delta x \Delta t}\]

さらに，

(243)\[<c>\cfrac{\partial h}{\partial t}+ h\cfrac{\partial<c>}{\partial t}+ \cfrac{1}{B} \left\{ <c>\cfrac{\partial(Bhu)}{\partial x}+ Bhu\cfrac{\partial<c>}{\partial x} \right\} =q_{su}-w_f c_b\]

(244)\[<c> \cancelto{\mbox{連続式より}=0}{\left\{ \cfrac{\partial h}{\partial t} + \cfrac{1}{B} \cfrac{\partial(Buh)}{\partial x} \right\}} + h\cfrac{\partial<c>}{\partial t} + hu \cfrac{\partial<c>}{\partial x} =q_{su}-w_f c_b\]

したがって,

(245)\[\cfrac{\partial<c>}{\partial t} + u \cfrac{\partial<c>}{\partial x} =\cfrac{1}{h}(q_{su}-w_f c_b)\]

なお, (245) 式において \(<c>\) と \(c_b\) に (235) 式の関係を用いると,

(246)\[\cfrac{\partial<c>}{\partial t} + u \cfrac{\partial<c>}{\partial x} =\cfrac{1}{h}(q_{su}-\alpha w_f <c>)\]

となります．ただし,

(247)\[\alpha=\cfrac{\beta}{1-\exp(-\beta)}, \; \; \beta=\cfrac{w_f h}{\epsilon}\]

です． さらに，浮遊砂濃度の拡散を考慮する場合, (246) の右辺に 拡散項を付加し，次式となります．

(248)\[\cfrac{\partial<c>}{\partial t} + u \cfrac{\partial<c>}{\partial x} = D\cfrac{\partial ^2<c>}{\partial x^2}+ \cfrac{1}{h}(q_{su}-\alpha w_f <c>)\]

この結果， (248) 式が水深平均濃度の連続式で，これを差分法で計算することになります． (248) 式は, (52) 式で示した, Source項を含む移流方程式と同じ形で, (52) 式における \(f\) を \(<c>\) に, \(G\) を \(D\cfrac{\partial ^2<c>}{\partial x^2}+\cfrac{1}{h}(q_{su}-\alpha w_f <c>)\) に置き換えたものとなり, 本テキストで用いてきたCIP法を用いることにより精度の高い計算が可能です． なお, \(<c>\) の計算では計算点を下図のように \(u\) の計算点の 間に取りますので，新たに \(<c>\) の計算点における \(u\) として \(u_x\) (249) 式のように定義し，これを (246) 式の移流速度 \(u\) として用いて計算に用います．

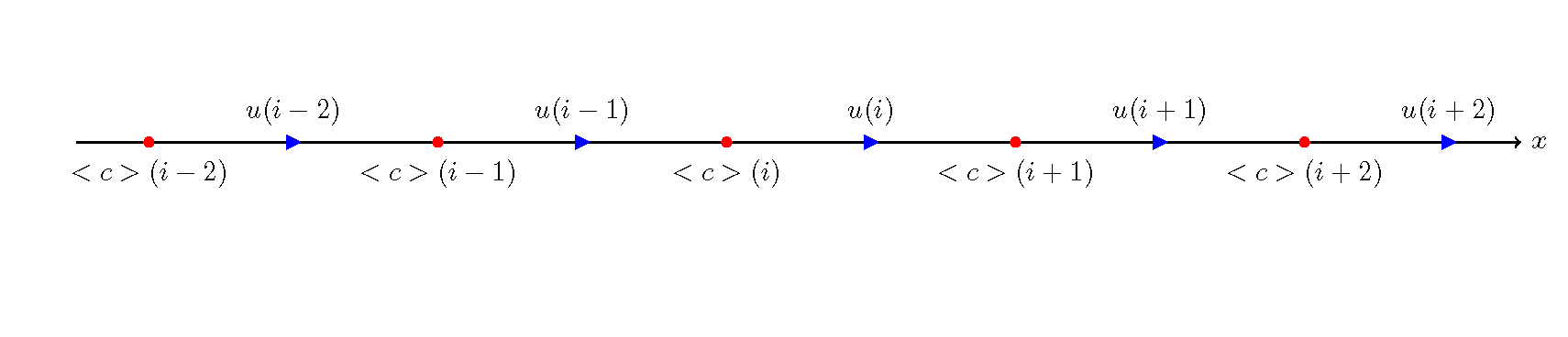
Figure 92 : 濃度計算点の配置

(249)\[u_x(i)=\cfrac{u(i)+u(i-1)}{2}\]

1次元浮遊砂による河床の連続式

水深平均濃度 \(<c>\) が求まると，河床における濃度 \(c_b\) も 同時に求まっていることになりますので，河床変動の計算は簡単です．

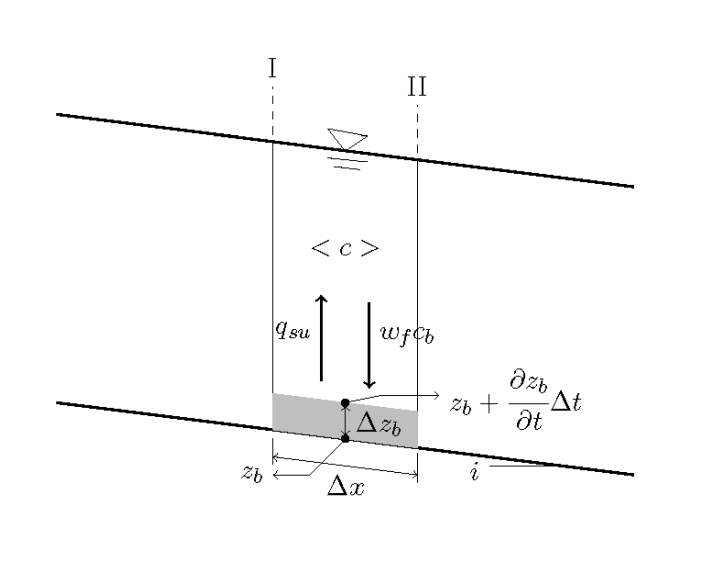
Figure 93 : 浮遊砂による河床変動模式図

(250)\[\cfrac{\partial z_b}{\partial t}= -\cfrac{1}{1-\lambda}(q_{su}-\alpha w_f <c>)\]

Pythonコード

上記計算手順に沿ったPythonコードはこちらです．

https://github.com/YasuShimizu/Bed-deformation-with-suspended-load

計算結果

上記計算コードを用いて行った貯水地への浮遊砂の堆砂の計算例を Figure 94 に示します． 計算条件は, 河床勾配 \(i=1/700\) , 延長 \(L\) =10km, 川幅 \(B\) =100(m), Manningの粗度係数 \(n\) =0.02, 河床材料の粒径 \(d\) =0.1mm, の長方形断面に流量 \(Q\) = 500m \(^3\) /s が 流下し, 下流端の水位が \(H\) =12mのダム貯水池を想定しています． なお，この計算例は 現場のための水理学(4) -浮遊砂と河床変動- で例題として掲載されている計算例と同じ条件で，計算結果も同じものが得られてます．

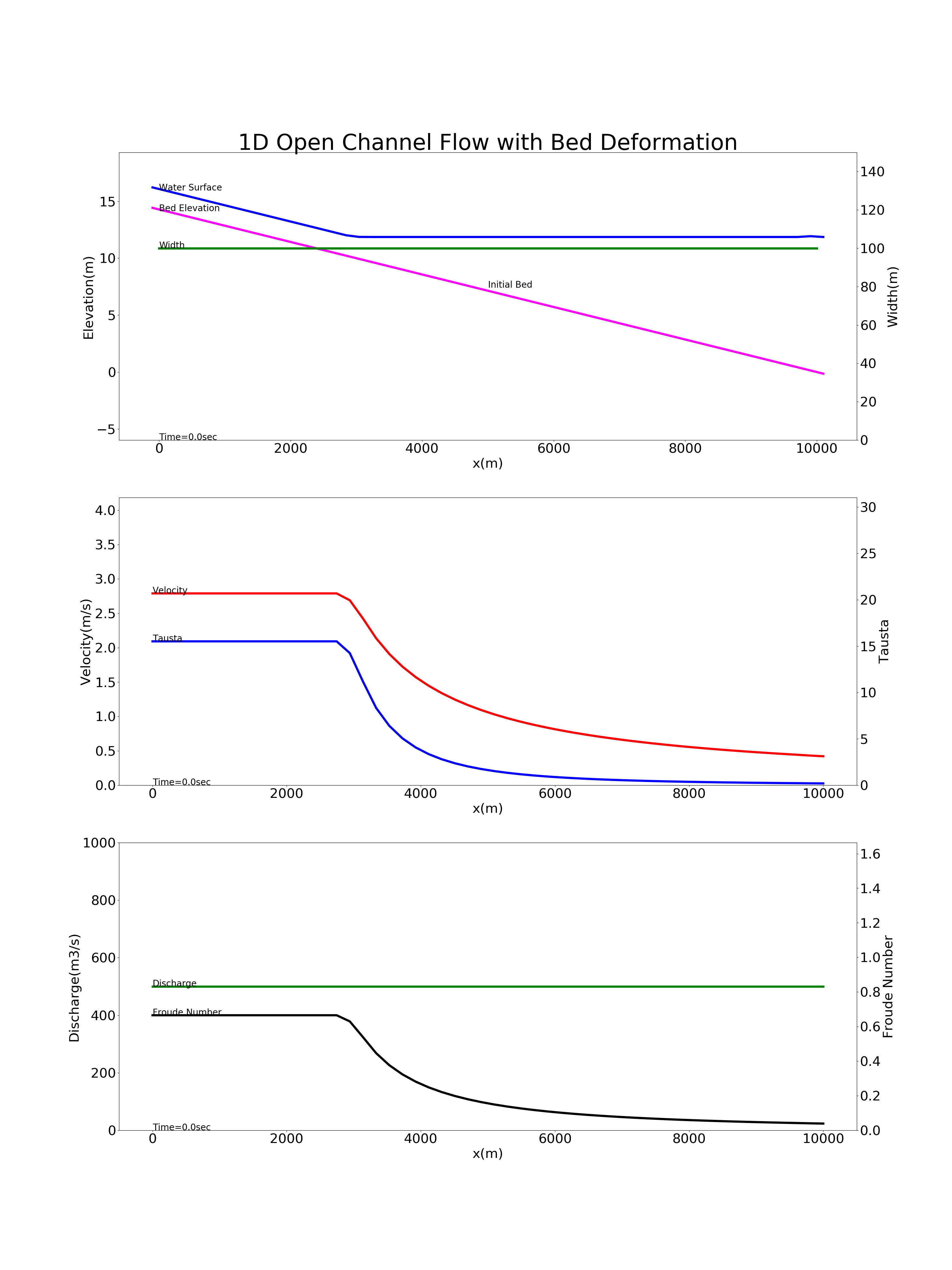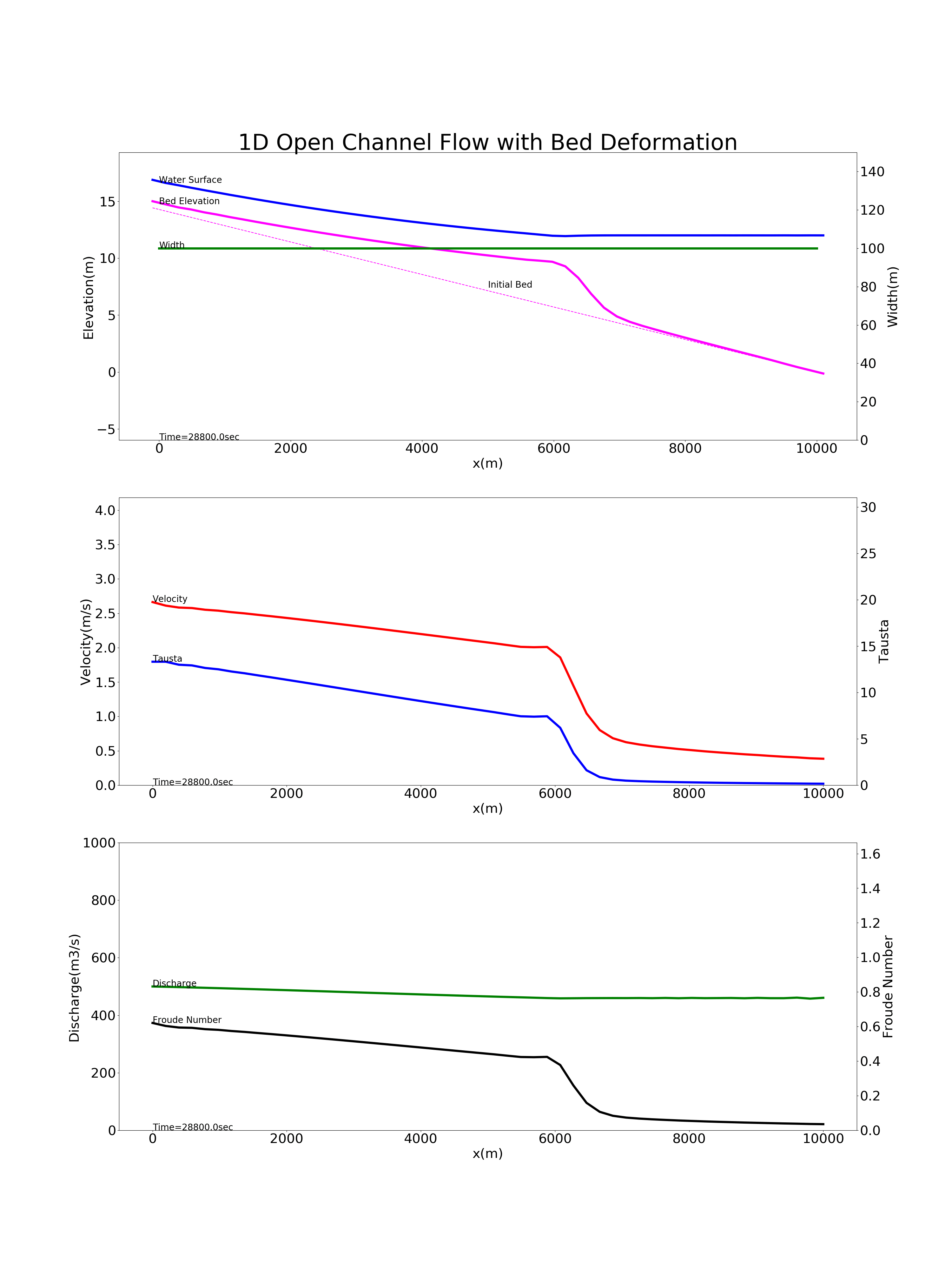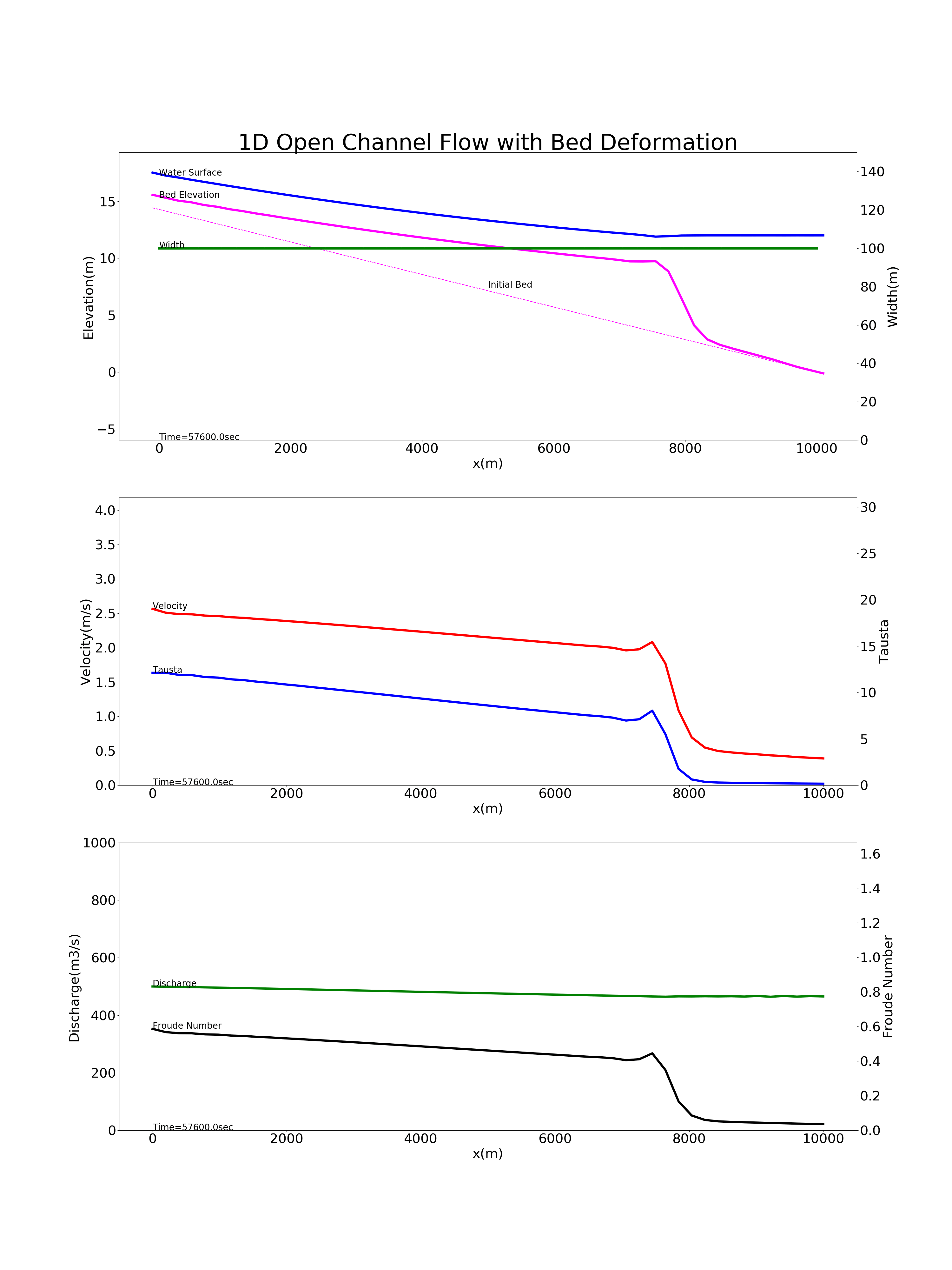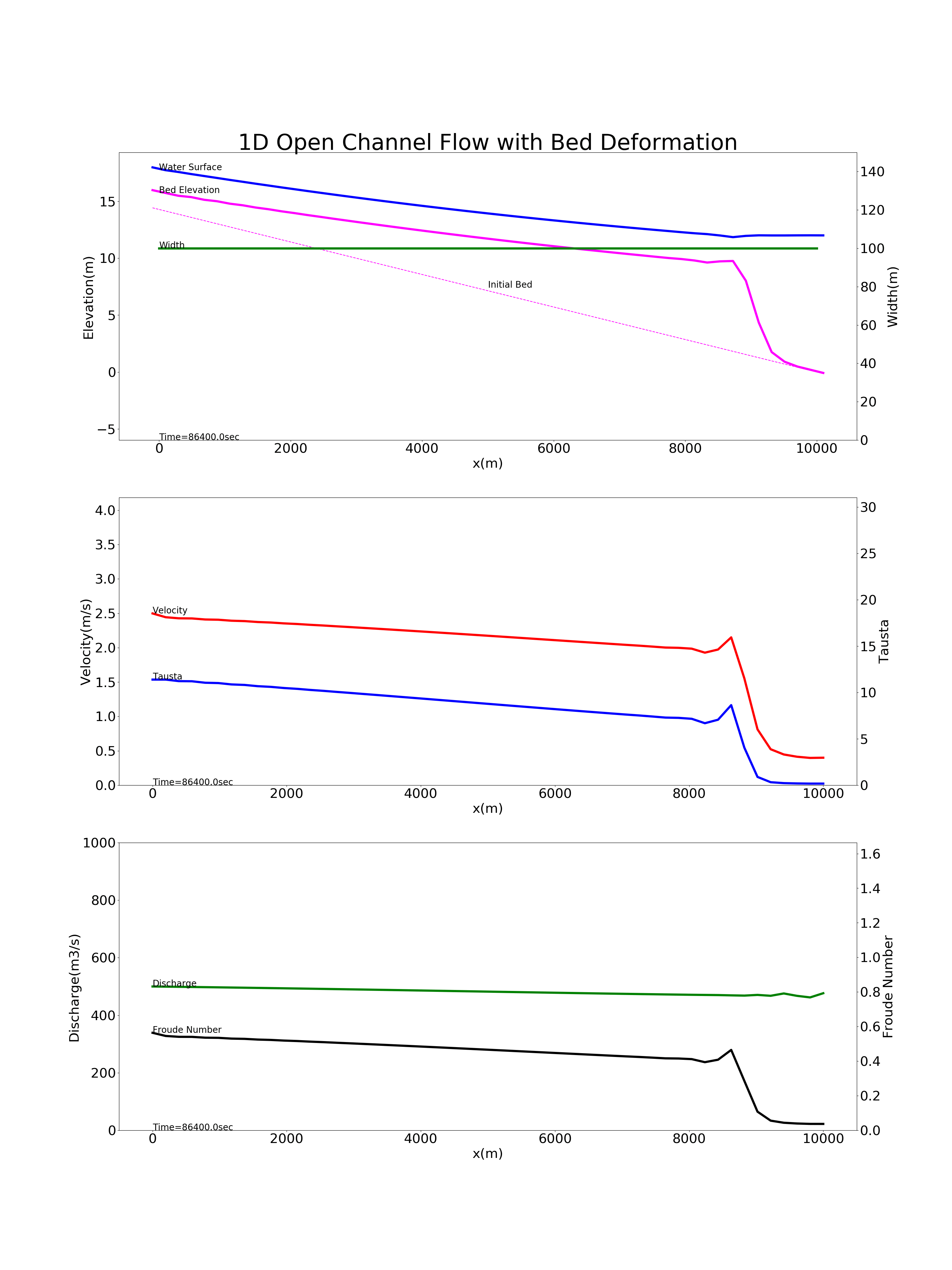
Figure 94 : 貯水地への浮遊砂の堆砂の計算