この節の作者: 清水康行 <yasu@i-ric.org>

本テキストへの感想, 質問, 要望, バグ報告などはこちらへお願いします.

川幅の変化を伴う2次元流れと河床変動計算

注釈

前節まで で一応の区切りを付けたつもりだったのですが， 先日 ICHARM の江頭先生を訪問した時に 急拡・急縮における平衡状態河床形とそれに対する流砂量式の違いに関する議論を頂き， 私も個人的に興味が湧いてきたので，あらたに本節を追加することにしました． 気が向いた時に自由に追加出来るのも，この手のWeb素材のメリットですね🤗

流下方向に川幅が変化する場合も連続式の計算は (266) 式の替りに． 近似的に次式で行うことが可能となります．

(316)\[\cfrac{\partial h}{\partial t}A_x(i,j) = Q_s(i-1,j)-Q_s(i,j)+Q_n(i,j-1)-Q_n(i,j)\]

ただし

(317)\[ \begin{align}\begin{aligned}Q_s(i,j)=u_s(i,j)\cfrac{h(i,j)+h(i+1,j)}{2}\Delta n(i,j)\\Q_n(i,j)=u_n(i,j)\cfrac{h(i,j)+h(i,j+1)}{2}\Delta s(i,j)\end{aligned}\end{align} \]

流砂連続式も同様に (315) 式において, \(\Delta n\) が 川幅の変化に応じて変化するので，(315) 式をそのまま用いることが 出来ます．

拡幅水路における計算例

流下方向に川幅が変化する水路の典型的な例として，急拡部を含む水路の計算例を示します． 以下の例は，河床勾配 \(i=1/500\) で上流側の水路幅30cmが水路中流部でで3倍の90cmに急拡する 水路に河床材料 \(d\) =1.35mmの均一粒径敷きつめ, 一定流量 \(Q\) =10 L/s の一定 流量を流した場合の流れと河床変動計算結果です. Figure 139 が河床高の時間変化, Figure 140 が水深と 水深平均流速ベクトル, Figure 141 が流量・流速および水位・河床高の 縦断分布です．

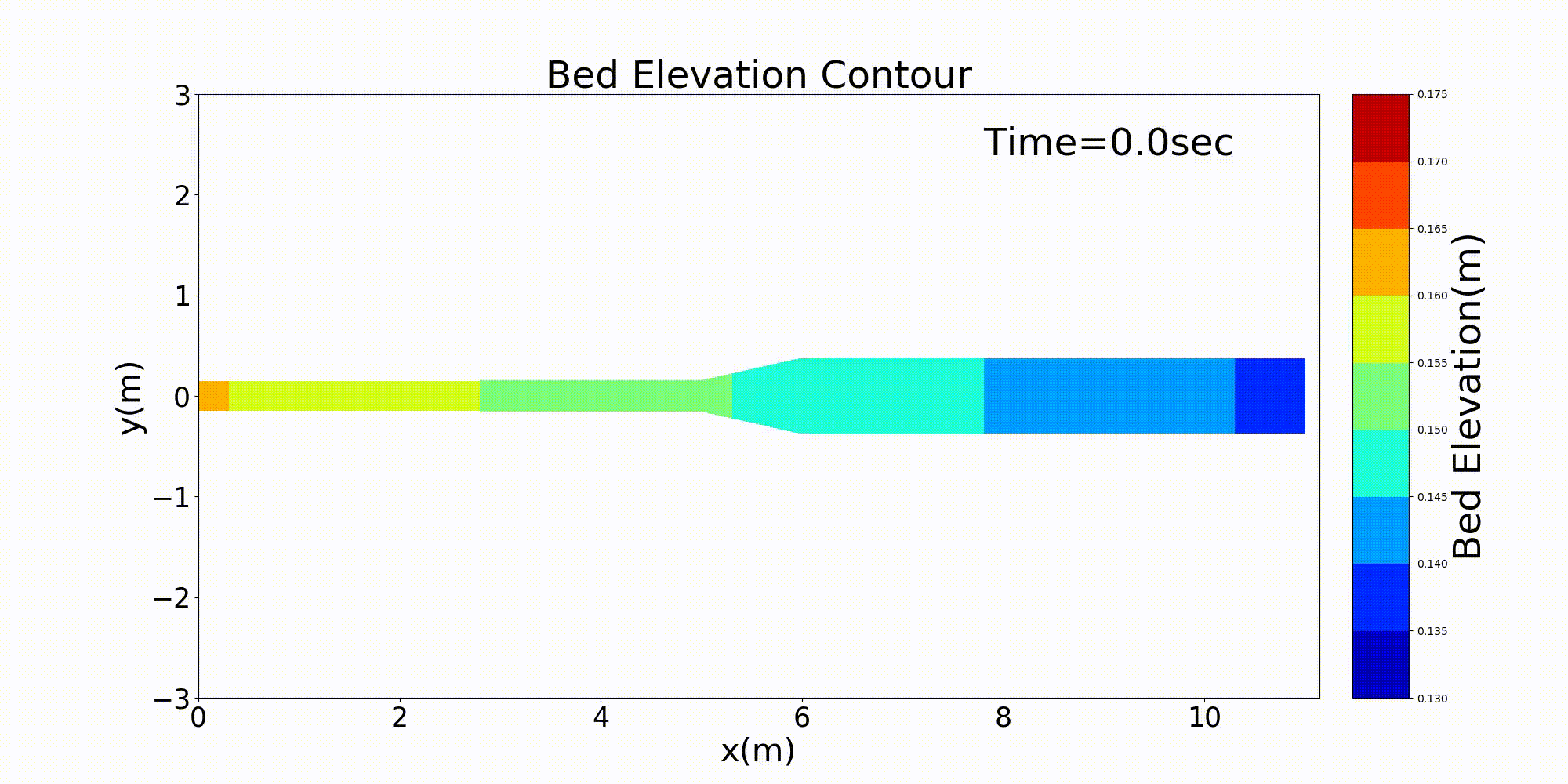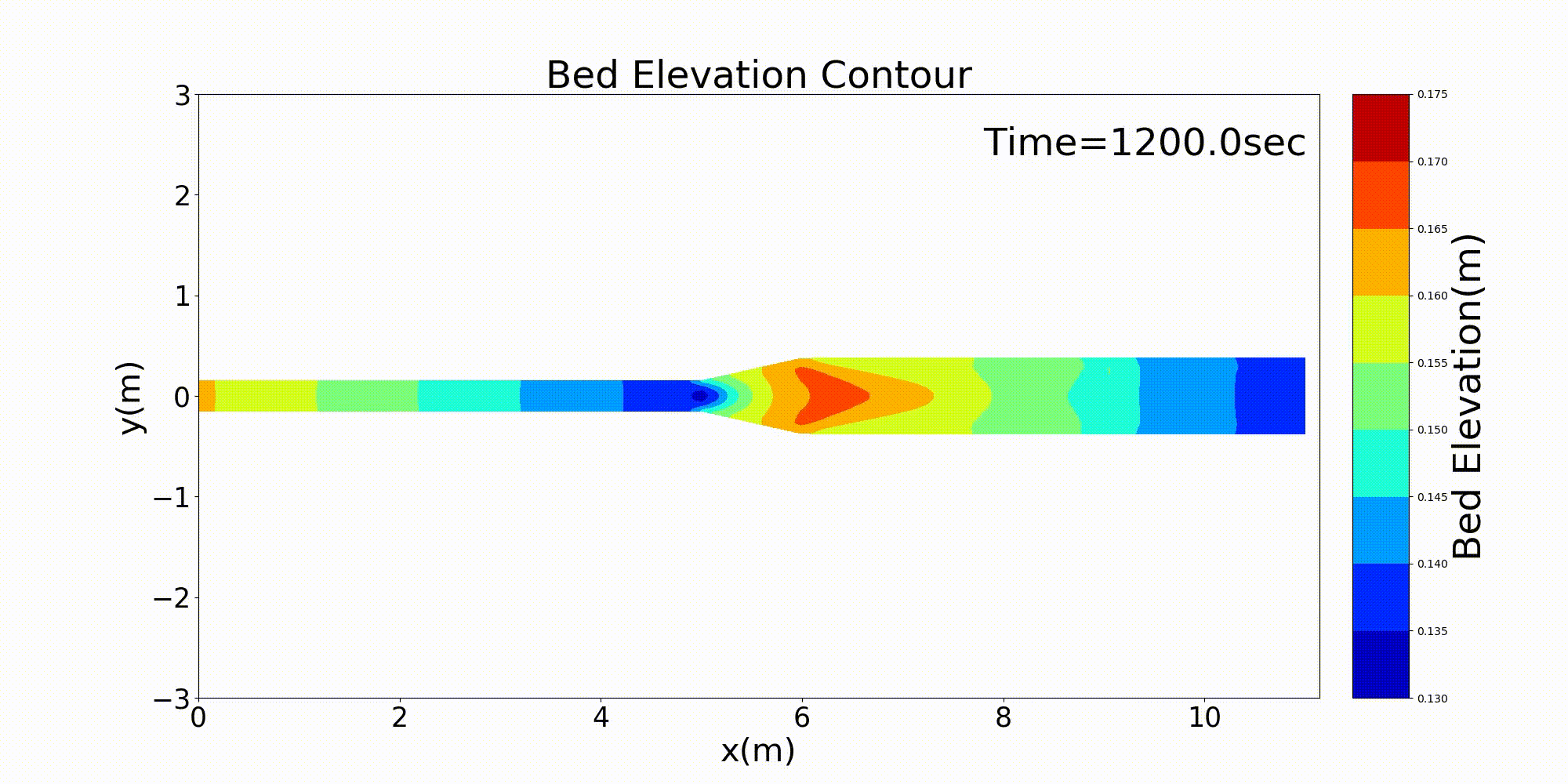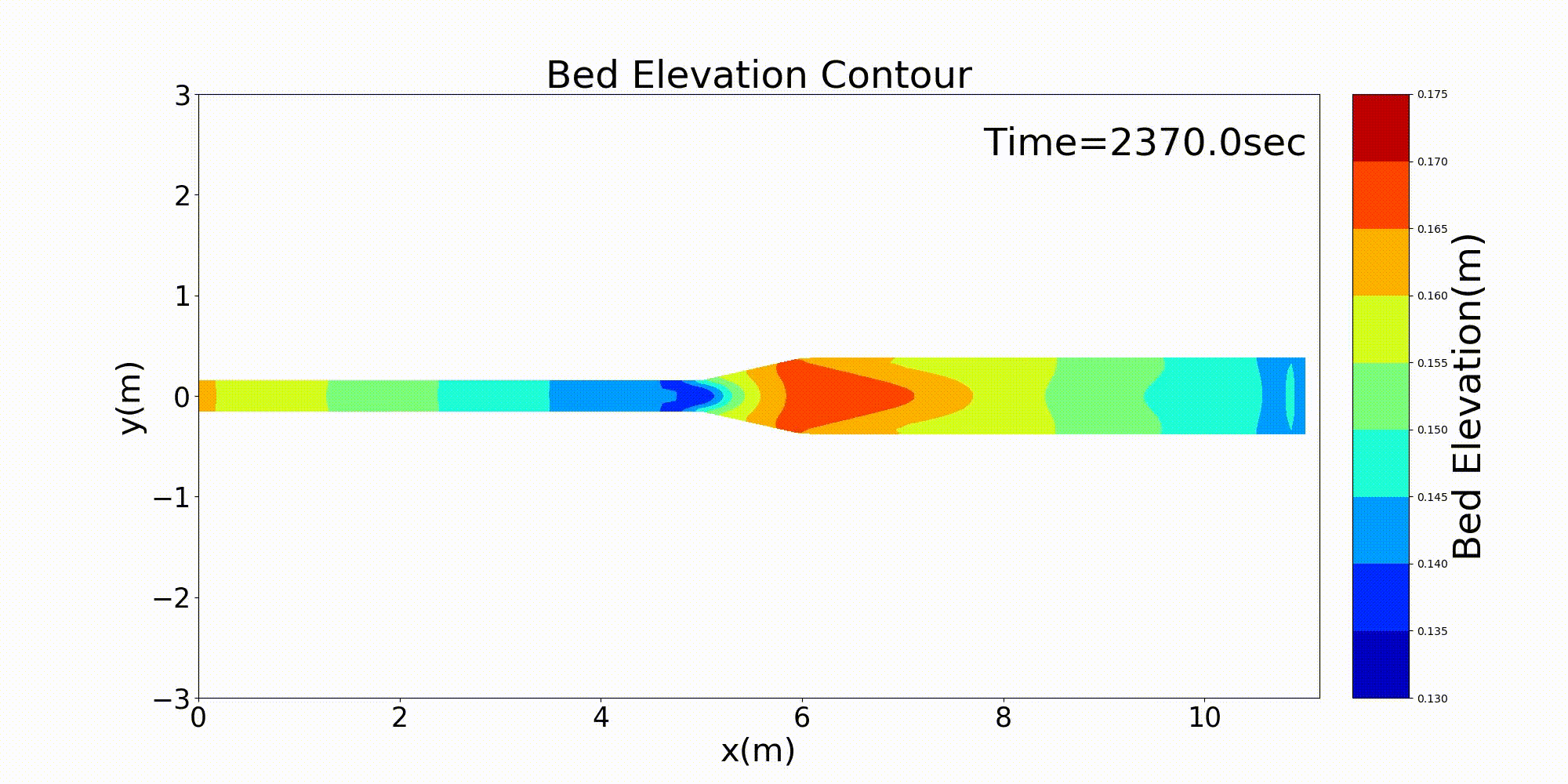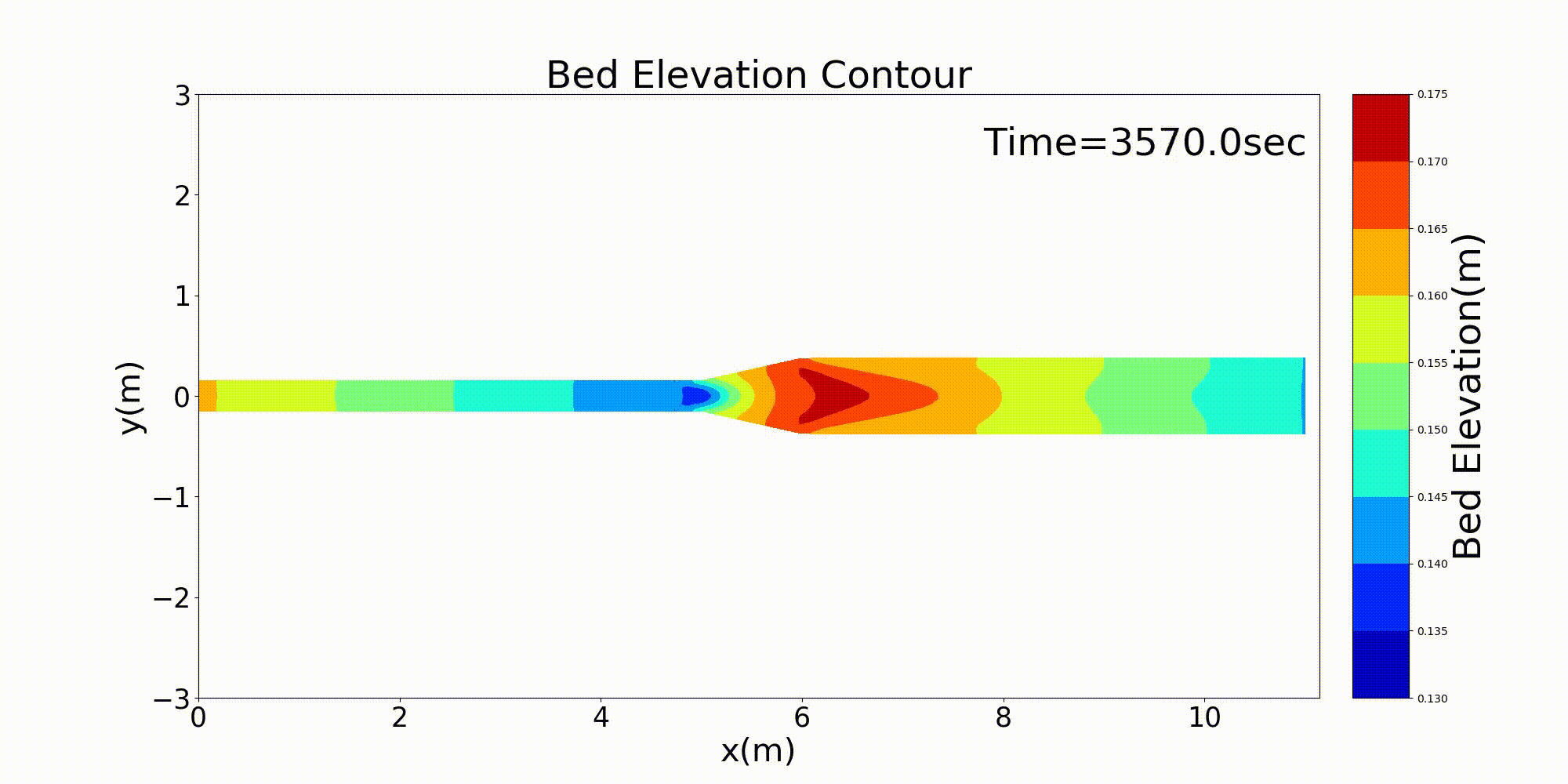
Figure 139 : 急拡水路における河床変動計算結果

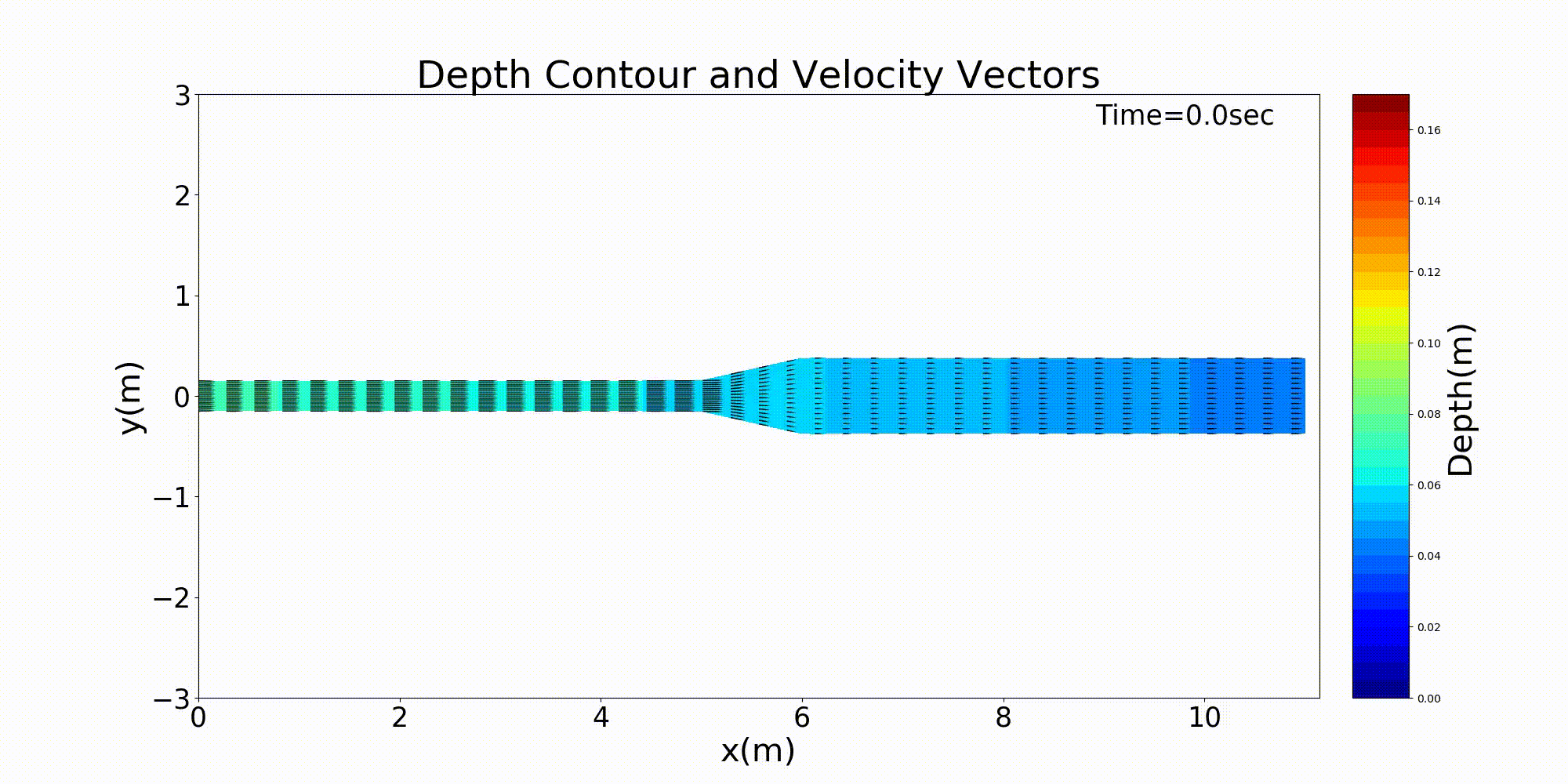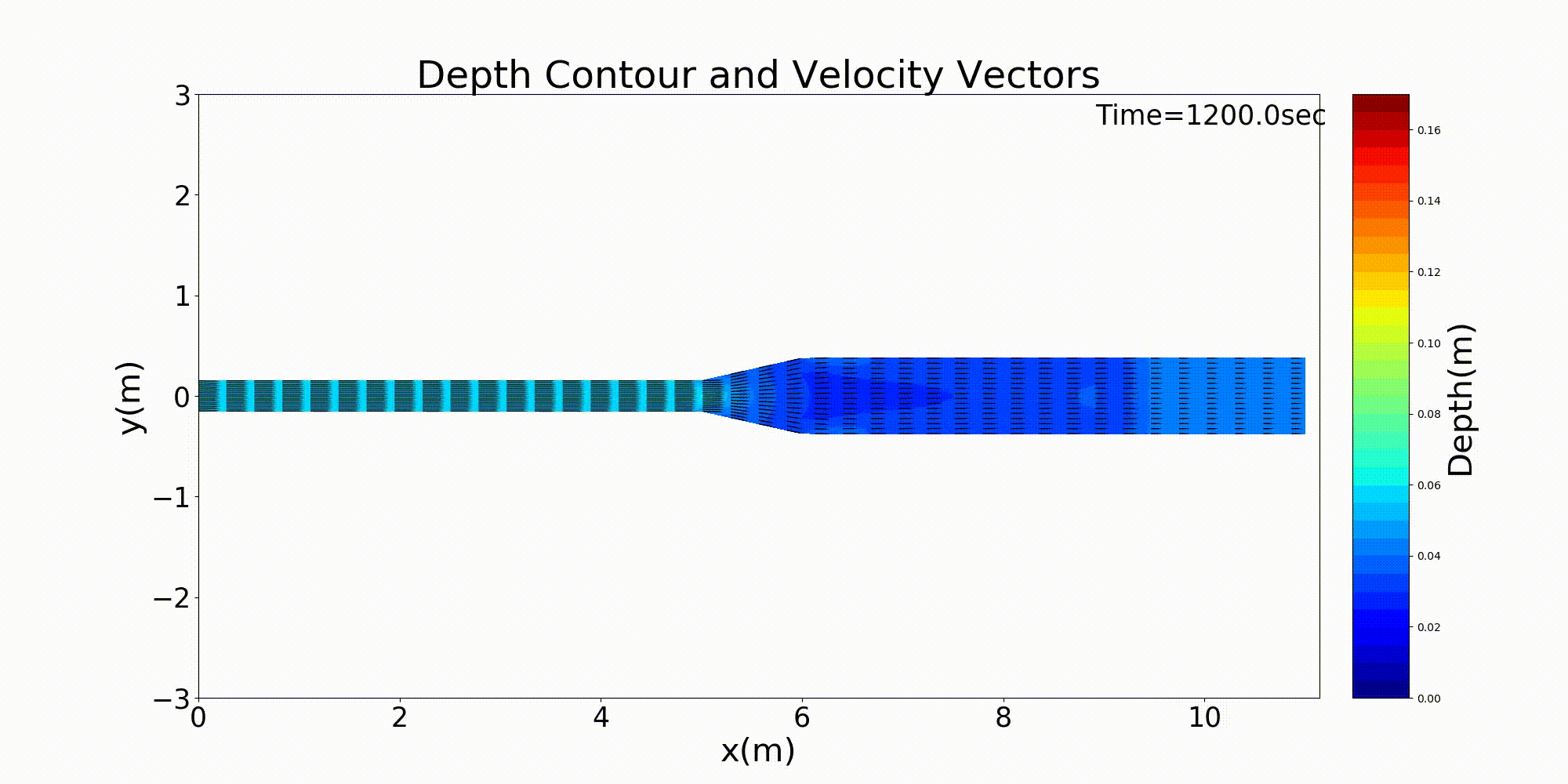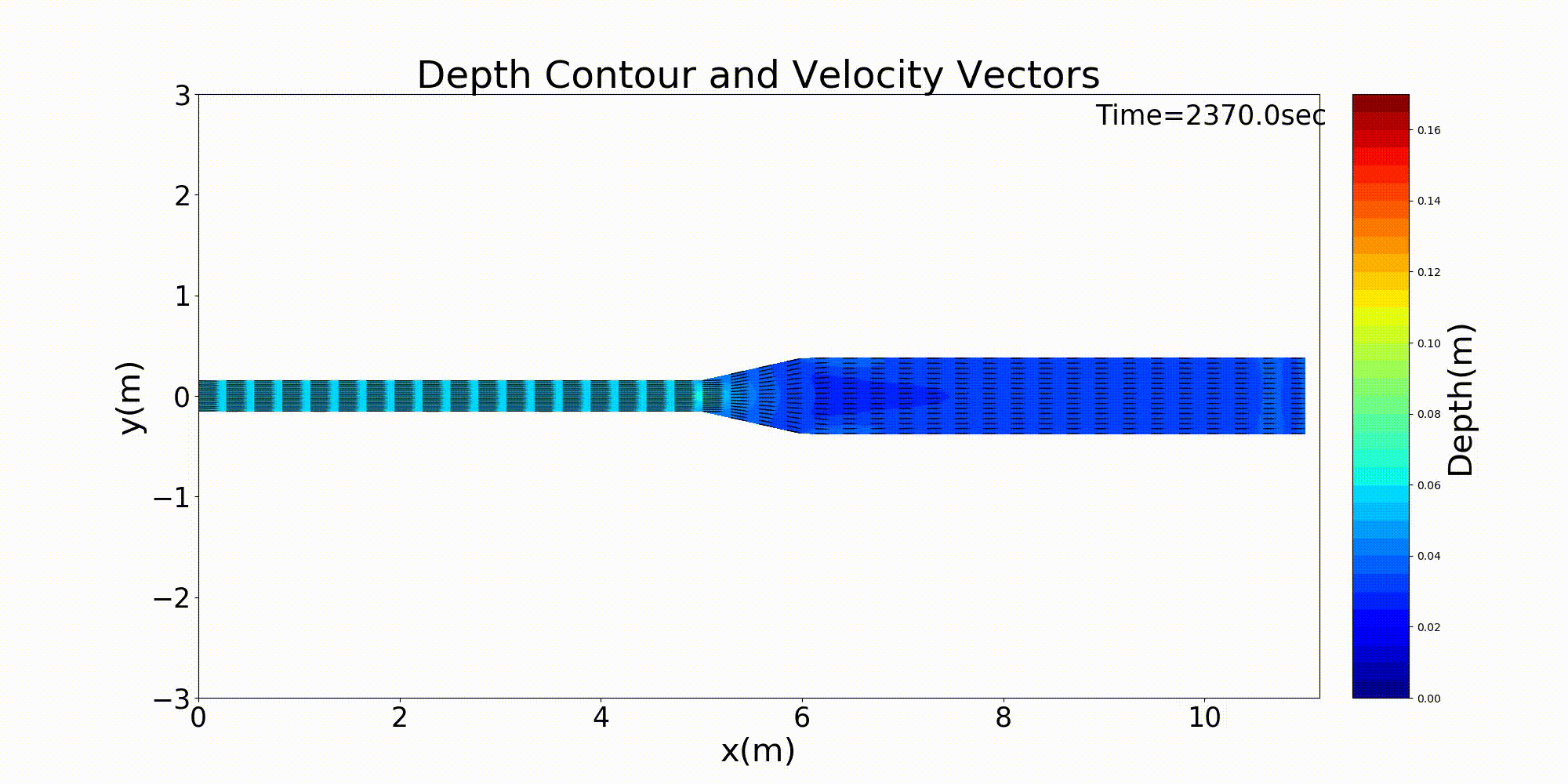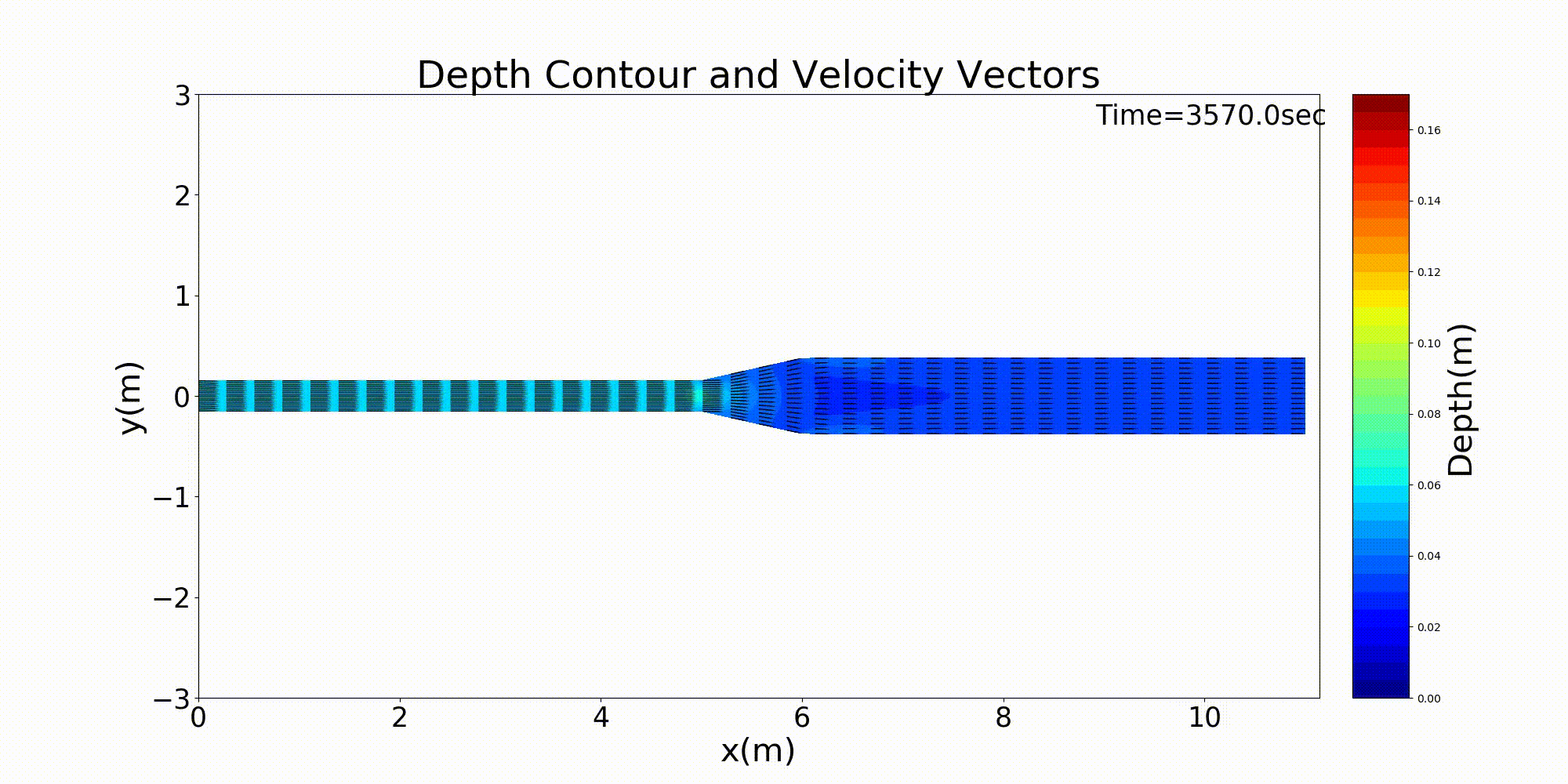
Figure 140 : 急拡水路における流速ベクトルと水深の変化計算結果

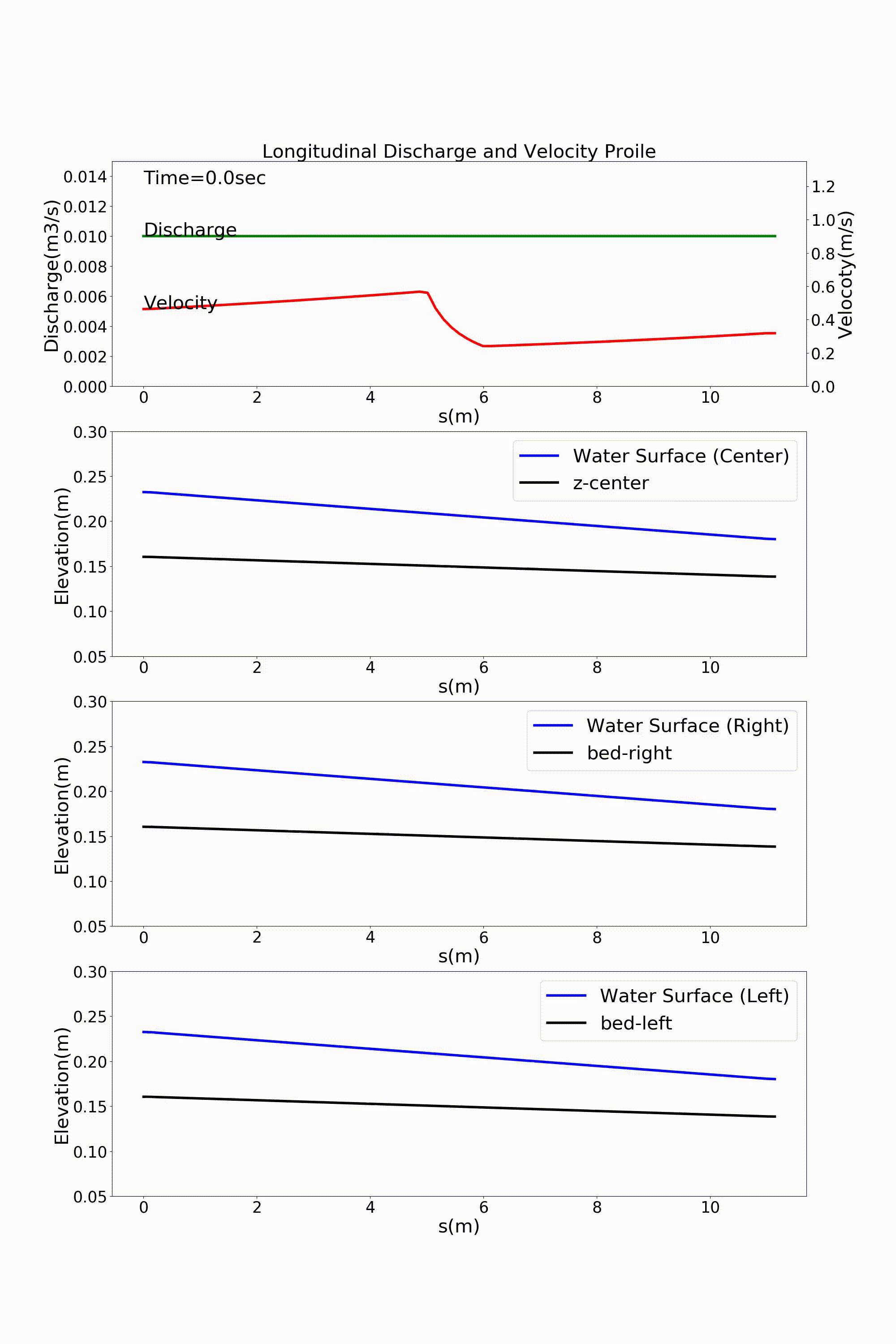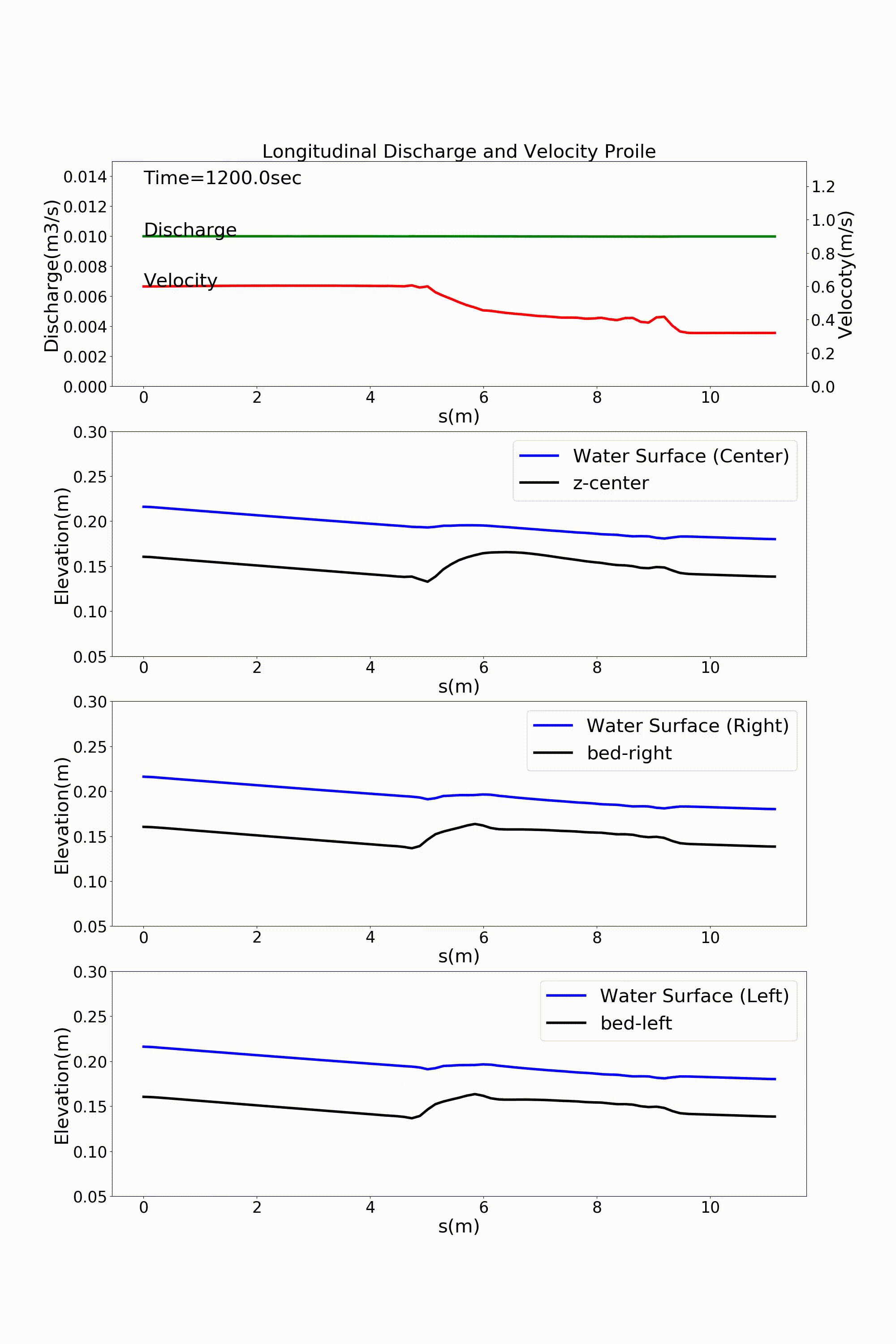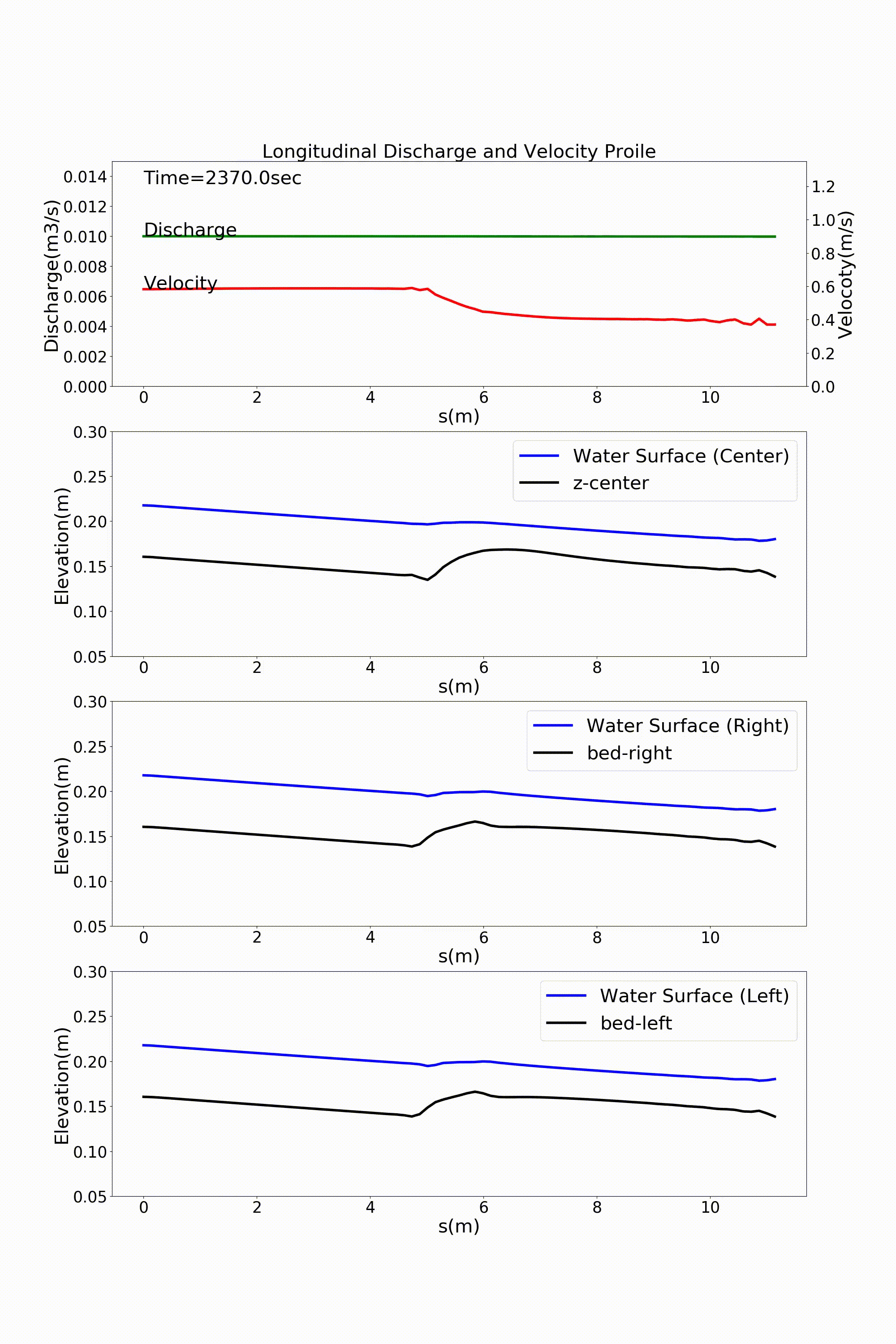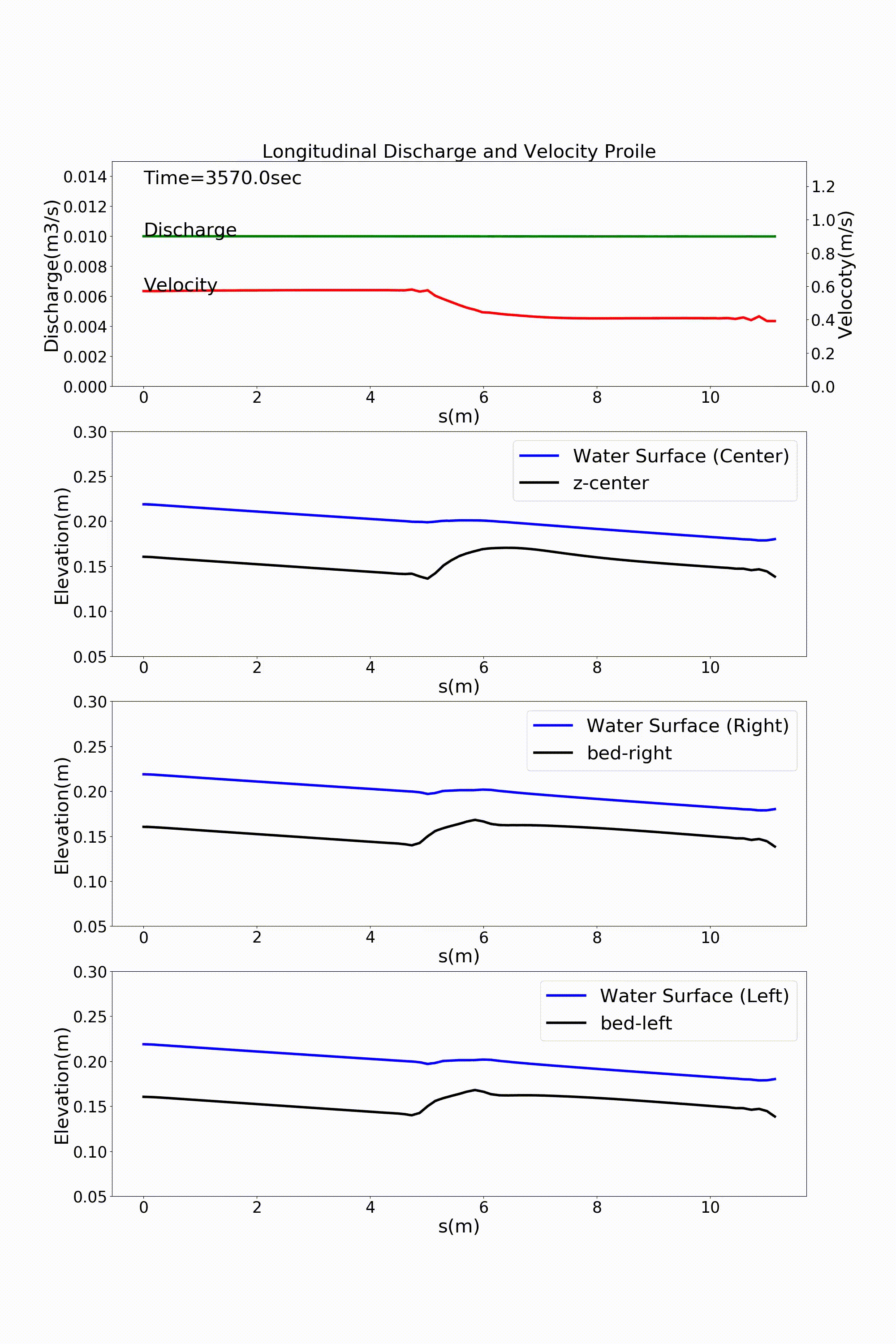
Figure 141 : 急拡水路における流量・流速の縦断分布, 河道中心・左岸・右岸に沿った 水位と河床高の縦断変化

Pythonコード

上記の計算例で用いた川幅変化伴う2次元流れと河床変動計算のPythonコードは こちらです．

https://github.com/YasuShimizu/2d_width_variation

この中のrun.pyを実行することで，上記計算例の計算の実施，作図，アニメーションの作成まで， 自動的に実行されます．なお，実行フォルダに下に bed, png, png_qという 3種類のフォルダを作成しておく必要があります．これらのフォルダの中に 時間ごとの計算結果のimageファイルが生成され，最後にアニメーションが生成 されます． 計算条件は下に示す，[Case1.yml]というファイルの中ですべて記述されてますので， これを適宜修正することにより違う条件での計算も可能です．

j_param: 1 #水路形状の与え方　1=一定勾配 2=データを読み込む
# j_param=1の場合
slope: 0.002 # 全体の勾配
eta_upe: 0.1606 #勾配で与える時の上流端の河床高
# j_param=2の場合
bed_file: Q10_xzb.csv
j_rep: 0 # 周期境界条件 0:周期境界条件無 1:周期境界条件

lam : 11 # 水路の波長(m)
nx0 : 80 # 格子数/1波長
ny : 15 # 横断方向格子数(奇数推奨)
wn : 1 # 波数
chb : 0.3 # 水路幅(m)
t0_degree : 0 # 最大蛇行偏角(Degree)

j_exp: 1 # 0=幅の変化無 1=幅変化あり
xb1: 5 # 幅の変化点
xb2: 6
xb3: 10
br0: 1.0 #幅の変化率
br1: 1.0
br2: 2.5
br3: 2.5
br4: 2.5

xsize: 20 # 計算結果をプロットする図の横スケール


amp : 0.0 # 初期河床砂州の波高(m)
delta : 0. # 初期河床砂州の位相差(m)
beta_0: 0. # 内岸で川幅を狭める割合
amp_0: 0.0 # 狭めた部分の河床高さ(m)

snu_0 : 1e-6 # 動粘性係数
hmin : 0.0001 # 最小水深(m)
vmin : 0.0001 # 最小流速(m/s)
cw: 0.001 # 側壁摩擦係数
ep_alpha: 1. # 渦動粘性係数の係数

qp: 0.01 # 流量(m^3/s)
snm: 0.0167 # マニング粗度
g: 9.8 # 重力加速度(m/s^2)
diam: 0.00135 # 河床材料平均粒径(m)
slambda: 0.4 # 空隙率
musk: 0.2 # μs×μk 静止摩擦係数×動摩擦係数
nsta: 7.0 # 2次流強度

j_west: 0 # 上流条件(0:開放, 1:閉鎖)
j_east: 0 # 下流条件(0:開放, 1:閉鎖)
j_hdown: 1 # 下流端水位条件(0:自由流出, 1:等流水深, 2:固定水位を与える)
h_down : 1. # j_hdown=2 の時の固定水位(m)
j_inih: 0 #初期水位縦断 0:直線 1:等流計算 2:不等流計算

alh: 0.7 # 水位収束計算のReluxsation係数
lmax: 10 # 各タイムステップでの水位収束計算最大回数

etime: 3600. # 計算終了時間(sec)
tuk: 30. # 計算結果アウトプット間隔(sec)
dt: 0.005 # 計算タイムステップ(sec)
stime: 0. # アウトプット開始時間(sec)
bstime: 20. # 河床変動開始時間(sec)

j_obst: 0 # 障害物の有無 0=無 1=有
jo_type: 2 # 障害物設置方法 1=ファイルから読む 2=条件を指定する
jo_method: 4 # 0=無 1=右岸のみ 2=左岸のみ 3=左右岸(千鳥) 4=左右岸(同位置)
f_dike_pos: 0.8 # 最初の水制の位置(m)
dike_dis: 0.8 # 水制間隔(m)
dike_length: 0.1 # 水制長(m)
dike_thick: 0.02 # 水制厚(m)
num_dike : 3 # 水制本数(方岸当たり)

iskip: 2 # ベクトルプロットの i 方向間引き
jskip: 1 # ベクトルプロットの j 方向間引き
jscale: 30 # 流速ベクトルのスケールファクター

alpha_upu : 0.1 # 周期境界条件の緩和係数
rrmax: 1 # 曲率プロットの軸最大値(1/m)
z_step: 0.005 #河床コンターのステップ

zhmin: 0.05 #河床・水位縦断図の最小値
zhmax: 0.3  #河床・水位縦断図の最大値