この節の作者: 清水康行 <yasu@i-ric.org>

本テキストへの感想, 質問, 要望, バグ報告などはこちらへお願いします.

蛇行河川流れの計算(実践編)

基礎式

蛇行河川の流路に沿って流下方向に \(s\) 軸, 横断方向に \(n\) 軸を取ります． \(s\) 軸は流路に沿って自由に左右に蛇行するものとしますが，\(n\) 軸は常に \(s\) 軸に直交することとした場合, この座標は 直交曲線座標 と呼ばれます． または，単に \(s-n\) 座標系と呼ぶ場合もありますが， 厳密には \(s-n\) 直交曲線座標系のことです．

\(s-n\) 座標系における流れの計算の基礎式の誘導はAppendixII( : x-y 座標と, s-n 座標 ) に示しますが，ここではその結果のみ再記します．

(263)\[\cfrac{\partial h}{\partial t} +\cfrac{\partial(hu_s)}{\partial s} +\cfrac{1}{r}\cfrac{\partial(rhu_n)}{\partial n} =0\]

(264)\[ \begin{align}\begin{aligned}{{\partial u_s}\over{\partial t}} +u_s{{\partial u_s}\over{\partial s}} +u_n{{\partial u_s}\over{\partial n}} -{{u_s u_n}\over{r}}= \hspace{4.5cm}\\-g\cfrac{\partial H}{\partial s} -{{g n_m^2 u_s \sqrt{u_s^2+u_n^2}}\over h^{4/3}} +\cfrac{\partial}{\partial s}\left(\nu_t\cfrac{\partial u_s}{\partial s}\right) +\cfrac{\partial}{\partial n}\left(\nu_t\cfrac{\partial u_s}{\partial n}\right) +\cfrac{\nu_t}{r}\cfrac{\partial u_s}{\partial n}\end{aligned}\end{align} \]

(265)\[ \begin{align}\begin{aligned}{{\partial u_n}\over{\partial t}} +u_s{{\partial u_n}\over{\partial s}} +u_n{{\partial u_n}\over{\partial n}} +{{u_s^2}\over{r}}= \hspace{4.5cm}\\-g\cfrac{\partial H}{\partial n} -{{g n_m^2 u_n \sqrt{u_s^2+u_n^2}}\over h^{4/3}} +\cfrac{\partial}{\partial s}\left(\nu_t \cfrac{\partial u_n}{\partial s}\right) +\cfrac{\partial}{\partial n}\left(\nu_t\cfrac{\partial u_n}{\partial n}\right) +\cfrac{\nu_t}{r}\cfrac{\partial u_n}{\partial n}\end{aligned}\end{align} \]

ここで, \(u_s, u_n\) は \(s, n\) 方向の水深平均流速, \(h, H\) は水深および水位, \(r\) は \(s\) 軸に沿った座標軸の曲率半径(上流から下流に向かって左カーブが \(r>0\) ), \(n_m\) はマニングの粗度係数, \(\nu_t\) は渦動粘性係数です.

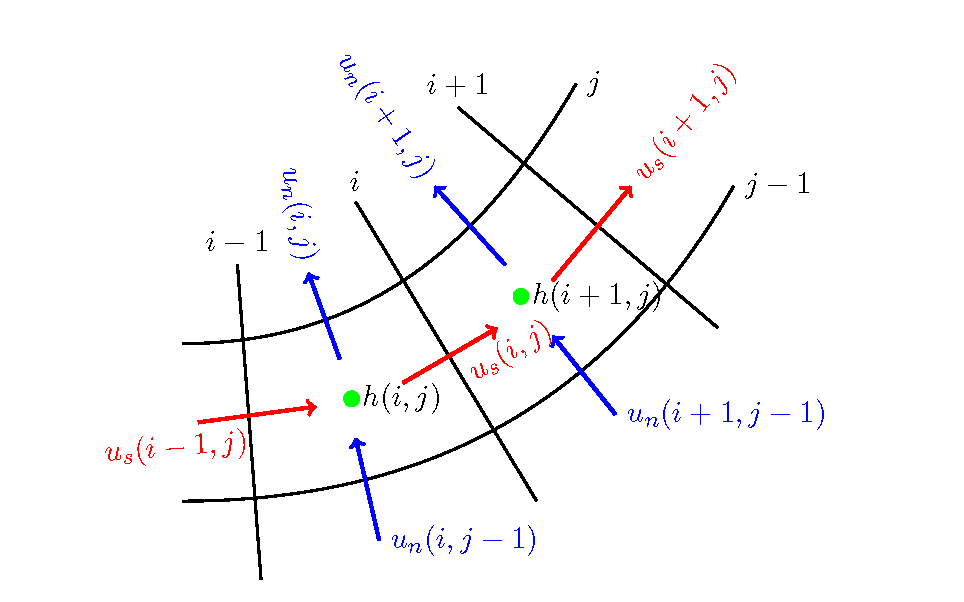
Figure 106 : \(u_s, u_n\) の計算点の配置

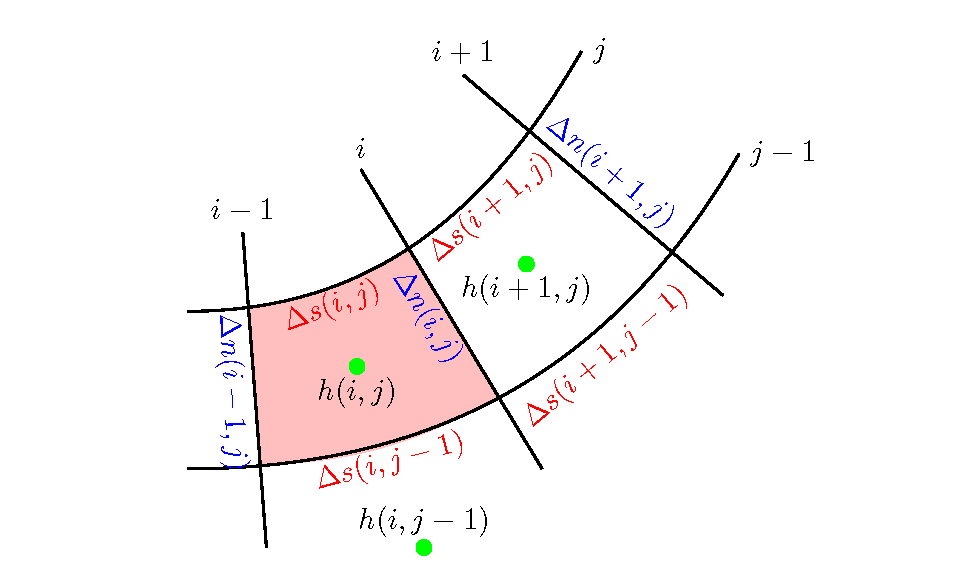
Figure 107 : \(\Delta s, \Delta n\) および \(h\) の計算点の配置

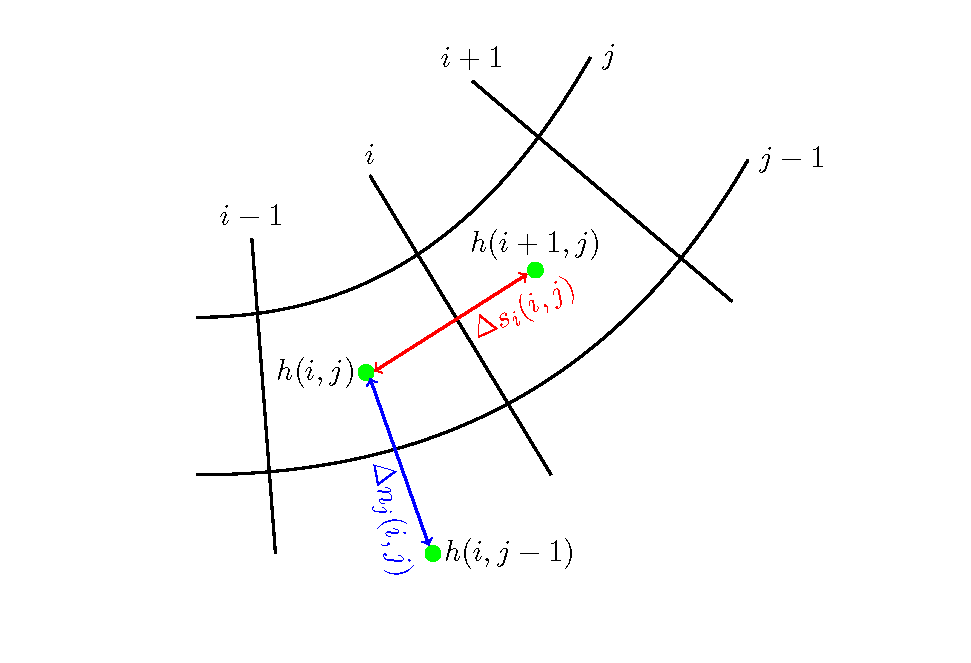
Figure 108 : \(\Delta s_i, \Delta n_j\) の配置

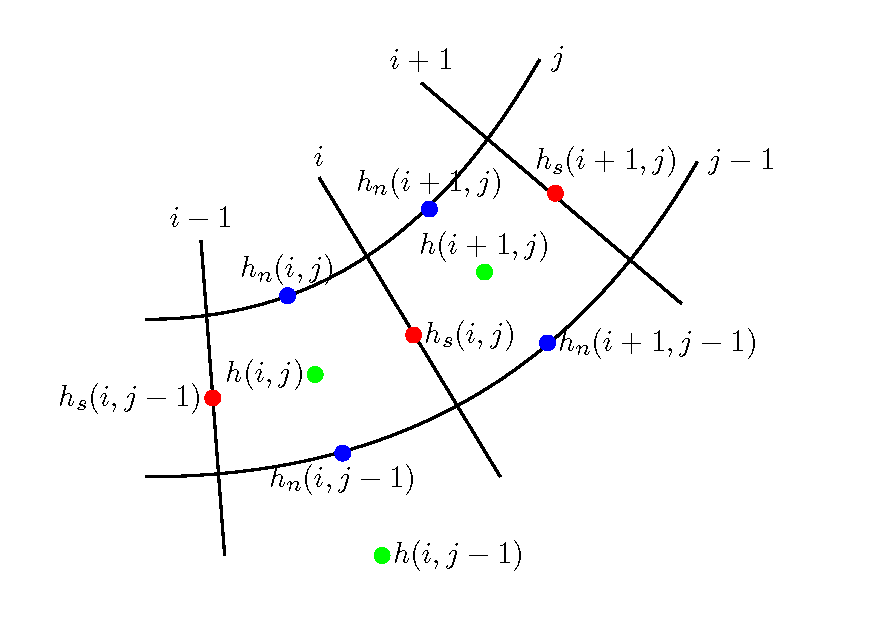
Figure 109 : \(h_s, h_n\) の配置

これらの変数配置および，格子幅を用いることにより， 例えば連続式 (263) 式は (439) 式と同様な考え方で 微小要素( Figure 107 のピンク色の部分)のFlux収支を考えることにより次式で表すことが出来ます．

(266)\[ \begin{align}\begin{aligned}\cfrac{\partial h}{\partial t}A_x(i,j) = \hspace{15cm}\\q_s(i-1,j)\Delta n(i-1,j)-q_s(i,j)\Delta n(i,j)+ q_n(i,j-1)\Delta s(i,j-1)-q_n(i,j)\Delta s(i,j)\end{aligned}\end{align} \]

ここで, \(q_s, q_n\) は \(s, n\) 方向の流量Flux(単位幅流量, 計算点の配置は Figure 106 の \(u_s, u_n\) と同じ)です. \(A_x(i,j)\) は微小要素の面積で近似的に

(267)\[A_x(i,j)=\cfrac{\Delta s(i,j)+\Delta s(i,j-1)}{2}\cdot \cfrac{\Delta n(i,j)+\Delta n(i-1,j)}{2}\]

で求められます．また,

(268)\[ \begin{align}\begin{aligned}q_s(i,j)=u_s(i,j) h_s(i,j)=u_s(i,j)\cfrac{h(i,j)+h(i+1,j)}{2}\\q_n(i,j)=u_n(i,j) h_n(i,j)=u_s(i,j)\cfrac{h(i,j)+h(i,j+1)}{2}\end{aligned}\end{align} \]

計算方法

基本的には 2次元自由水面非定常流 で解説した直交座標系における2次元計算と 同じ方法になりますが，直交座標の計算で用いた \(\Delta x, \Delta y\) の替わりに, Figure 107 に示す流路の局所的な曲率の変化を考慮した \(\Delta s, \Delta n\) を用いることにより, ほぼ 2次元自由水面非定常流 で示した方法と同じ方法で計算することが出来ます．

\(s, n\) 方向の運動方程式である, (264) 式および (265) 式と, 直交座標 \(x, y\) 方向の運動方程式, (146) 式および (147) 式を比較すると, 左辺に \(-\cfrac{u_s u_n}{r}\) および, \(\cfrac{u_s^2}{r}\) などの項が加わっています． これらは，流路の曲がりに伴う付加的な加速度を表す項なので，これらの項については Non-Advection Phase において追加する必要があります．

具体的には (153) 式および (157) 式の替わりに,

(269)\[{{\partial u_s}\over{\partial t}}= -g\cfrac{\partial H}{\partial s} -{{g n_m^2 u_s \sqrt{u_s^2+u_n^2}}\over h^{4/3}} +{{u_s u_n}\over{r}}\]

(270)\[{{\partial u_n}\over{\partial t}}= -g\cfrac{\partial H}{\partial n} -{{g n_m^2 u_n \sqrt{u_s^2+u_n^2}}\over h^{4/3}} -{{u_s^2}\over{r}}\]

を用い, この結果Non-Advection Phase Iにおける (162) 式および (163) 式に相当する式は下記となります．

(271)\[\overline{u_s}= u_s^n +\Delta t\left\{ - g{{\partial \overline{h}}\over{\partial s}} - g{{\partial \eta}\over{\partial s}} - g{{n_m^2 \overline{u_s}\sqrt{\overline{u_s}^2 +\overline{u_{ns}}^2}} \over{\overline{h_s}^{4/3}}} +{{\overline{u_s}\; \overline{u_{ns}}}\over{r_s}}\right\}\]

(272)\[\overline{u_n}= u_n^n+\Delta t\left\{- g{{\partial \overline{h}}\over{\partial n}} - g{{\partial \eta}\over{\partial n}} - g{{n_m^2 \overline{u_n}\sqrt{\overline{u_{sn}}^2 +\overline{u_n}^2}} \over{\overline{h_n}^{4/3}}} -{{\overline{u_{sn}}^2}\over{r_n}} \right\}\]

ここで, Over Bar付き記号は Non-Advection Phase I の値であることを示し， (266) の連続式と連立して繰り返し計算で求める値です． \(h_s, u_{ns}\) は \(u_s\) の計算点における水深および \(n\) 軸方向流速, \(h_n, u_{sn}\) は \(u_n\) の計算点における水深および \(s\) 軸方向の流速で, \(u_{ns}, u_{sn}\) は次式となります.

(273)\[ \begin{align}\begin{aligned}u_{ns}(i,j)=\cfrac{u_n(i,j)+u_n(i+1,j)+u_n(i,j-1)+u_n(i+1,j-1)}{4}\\u_{sn}(i,j)=\cfrac{u_s(i,j)+u_s(i,j+1)+u_s(i-1,j)+u_s(i-1,j+1)}{4}\end{aligned}\end{align} \]

\(r_s\), \(r_n\) はそれぞれ, \(u_s\) および u_n の計算点における曲率半径で, 今, 計算格子点における \(s\) 軸に沿った曲率半径を (262) で各格子点で定義する場合, 曲率半径の逆数である曲率を,

(274)\[\rho_r(i,j) = \cfrac{1}{r(i,j)}\]

として, \(r_s, r_n\) は次式となります.

(275)\[ \begin{align}\begin{aligned}\cfrac{1}{r_s(i,j)}=\cfrac{\rho_r(i,j)+\rho_r(i,j-1)}{2}\\\cfrac{1}{r_n(i,j)}=\cfrac{\rho_r(i,j)+\rho_r(i-1,j)}{2}\end{aligned}\end{align} \]

他の計算方法はすべて前記の 2次元自由水面非定常流 と同じなので，ここでは省略します．

Dry Bed (水が無い計算点での処理)

前節[ 河床に砂州状の形状を与える ]で述べたような砂州状の河床形状を与えたり， 後に述べる河床変動計算において砂州などの影響で河床が上昇して来るような 場合，連続式 (266) 式による水深の計算で水深がゼロになり， 水の無い計算セルが現れる場合があります．実際は (266) の計算で水深がマイナスに なる場合もあり，この場合は便宜的にゼロに戻すという操作が行われます． 運動方程式 (264) 式, (265) 式においても右辺第２項の分母に水深 \(h\) が含まれるため発散して，水深がゼロもしくはゼロに近付くと発散 しまいます． 水深がゼロのセルでは単純に流速もゼロなのですが，スタッカード格子を採用している 場合，セル中心の水深がゼロでも，セルのエッジで計算している流速がゼロにならない 場合も想定され，この場合の計算の取り扱いには注意が必要です． このような水深がゼロとなる計算点はDry Bed(乾いた河床)と呼ばれ，計算上特殊な処理が必要になります．

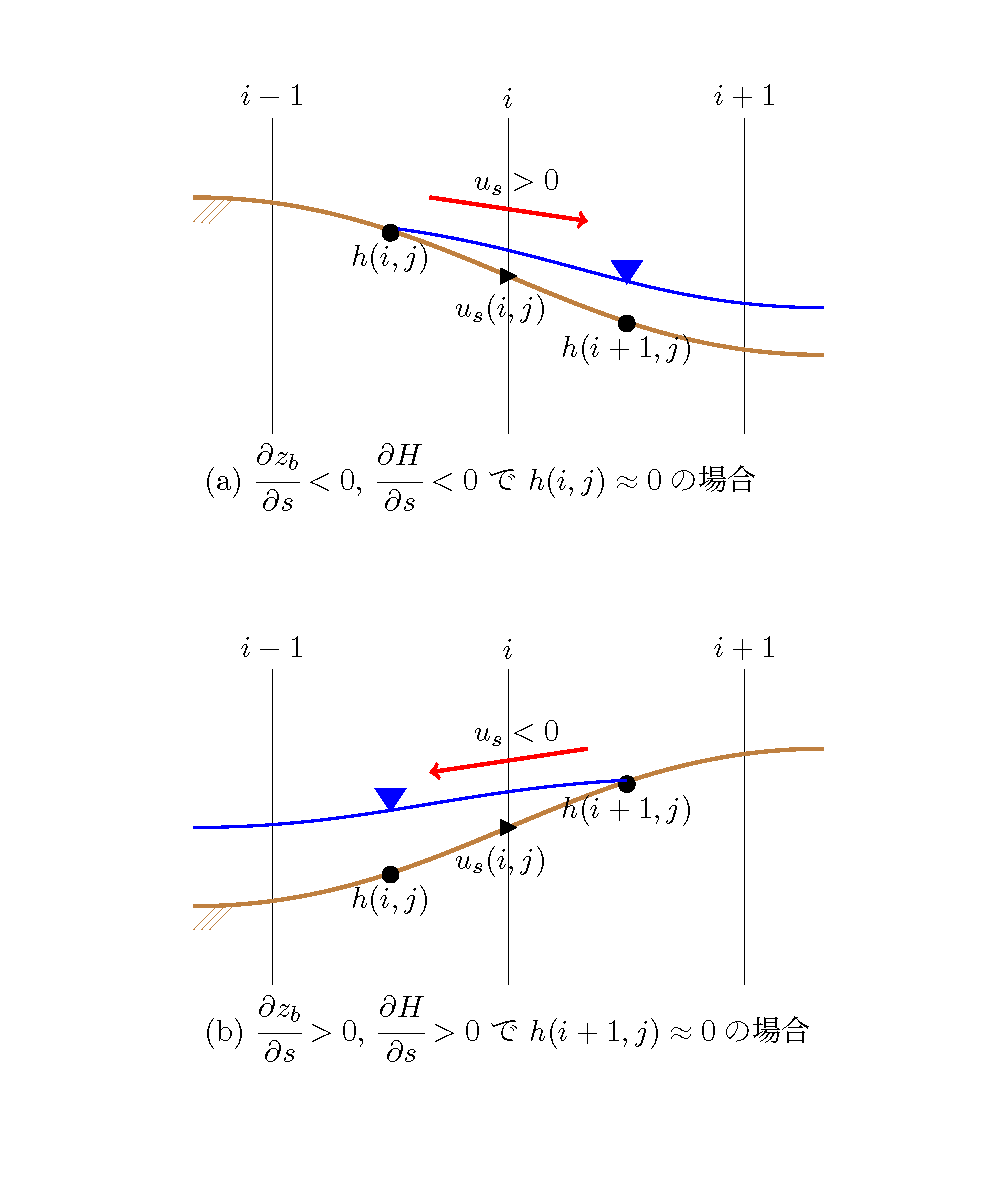
Figure 110 : Dry bedの処理

例えば \(u_s\) の計算をする場合，その計算点を挟む上下流の水位(水面勾配) が必要になりますが，そのどちらかの水深がゼロの場合，河床および水深の状況は水深の状況や河床勾配・水面勾配 の状況別に Figure 110 のような状況が想定されます． これらの計算点において，水面勾配を図のように水深がゼロの場合は地盤高で代用してしまうと， 斜面から水が湧き出して来たり，地盤に水が吸い込まれてしまうような，非現実的な流れが生じてしまうとともに 各セルにおいて連続式が満たされない状況が生ずるため，それぞれの状況に応じた適切な処置が必要になります．

この処理法については更なる検討が必要ですが，ここでは単純に，Figure 110 のような状況においては， 対象とする流速計算点を挟む水面勾配をゼロとするという近似的な扱いをすることとしました． Figure 110 の状況は \(s\) 軸方向に \(u_s\) を計算する場合の扱いですが， \(n\) 軸方向に \(u_n\) を計算する場合も全く同じく扱うことにしました．

Pythonコード(試作版)

砂州状河床形状を伴い蛇行水路の2次元非定常流れの計算モデルのPythonコード(試作版)は 下記からダウンロード可能です. 計算方法の詳細手順や境界条件，初期条件などは ソースコードを参照願います．このコードを実行すると (1)流量, 水位および河床形の縦断分布図(水路中心, 右岸側壁, 左岸側壁), および, (2)水深コンター図と流速ベクトル図が生成されます． これらは，それぞれの時間変化を示すgifアニメーションファイルおよびmpeg形式の動画で 生成されます．アニメーションを作成するための各コマの画像を保存するために，実行ファルダの下に png, png_q, png_r という名前を予め作ってから実行して下さい． (png_rのフォルダは次節で解説する流線の曲率の縦分布のプロット用のフォルダです)

https://github.com/YasuShimizu/Nays2d_sn_python

注釈

上記コードは試作版ですのでバグ報告，簡素化や高速化のアイデア，機能の付加など様々なご意見， ご助言を頂ければ幸いです．ご質問も可能な範囲でお答えしますので， 何かございましたら yasu@i-ric.org まで連絡お願いします．

Sin-Generated Curve水路における計算例

蛇行波長 \(L\) =3m, 波数2, 水路幅 \(B\) =0.4m, 最大蛇行偏角 \(\theta_0\) =40 \(^\circ\) , 水路勾配 \(I\) =0.001のSine-Generated Curve水路に波高 \(A_p\) =0.015m, 位相差 \(\delta_s\) =0.2mの (255) 式で表される砂州形状を付加した水路における流れの計算を行います． 計算に用いる水路形状と河床形状を Figure 111 に示します.

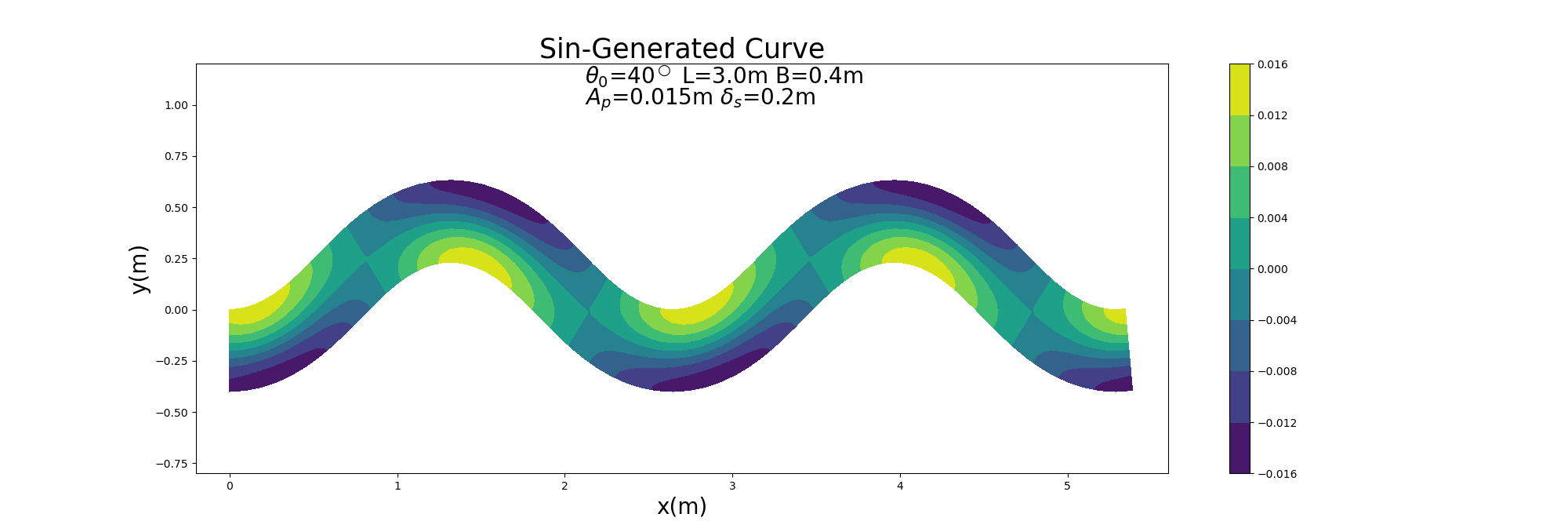
Figure 111 : 計算に用いるSin-Generated Curve水路

この水路に，\(Q\) =0.001 m \(^3\) /s, の流量が流れた場合の流れの計算を行います．ただし, マニングの粗度係数 \(n_m\) =0.012 とし， 計算格子の数は流下方向に1波長当り41 \(\times\) 2波長で82, 横断方向に21とします.

計算結果を以下に示します． この例では，蛇行水路内に砂州状の河床を配置してあり, 左右交互に水の無い浮州が出ますが， 現在の試作版のコードでは汀線の扱いが必ずしも的確ではないため，汀線近傍で流れが不安定になってます． これについては今後の要改良点ですが，読者の皆様も何か良いアイデアがあればお聞かせ下さい．

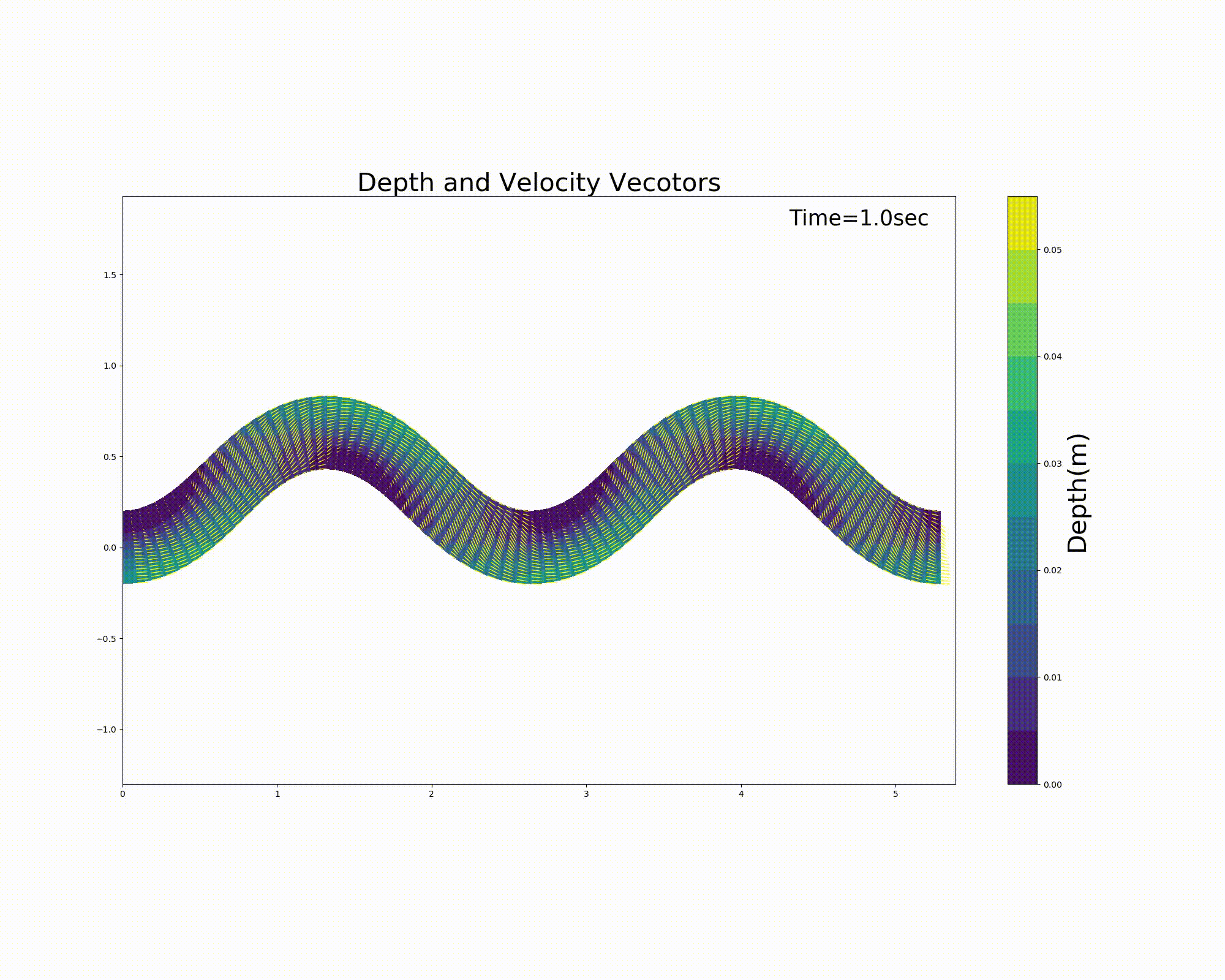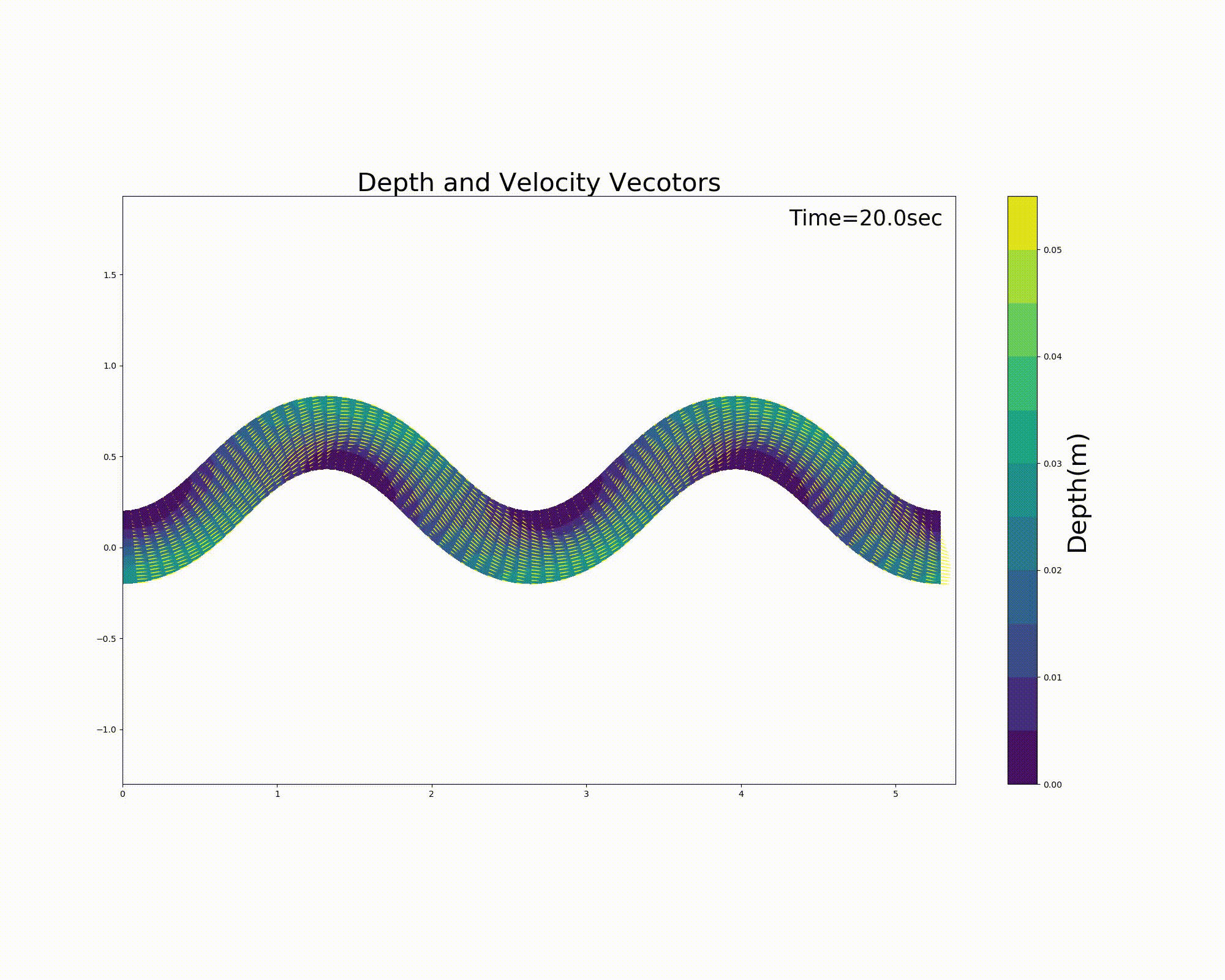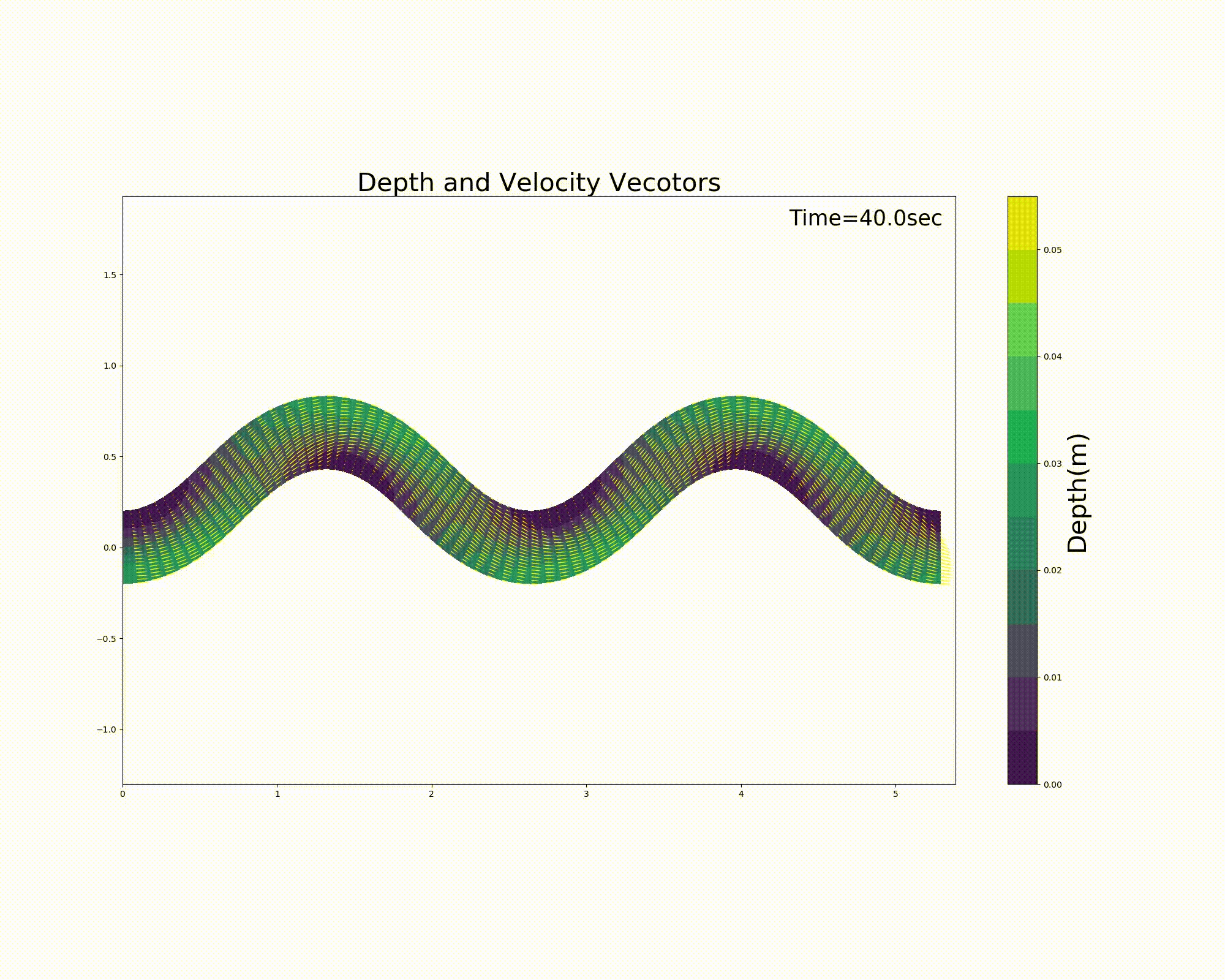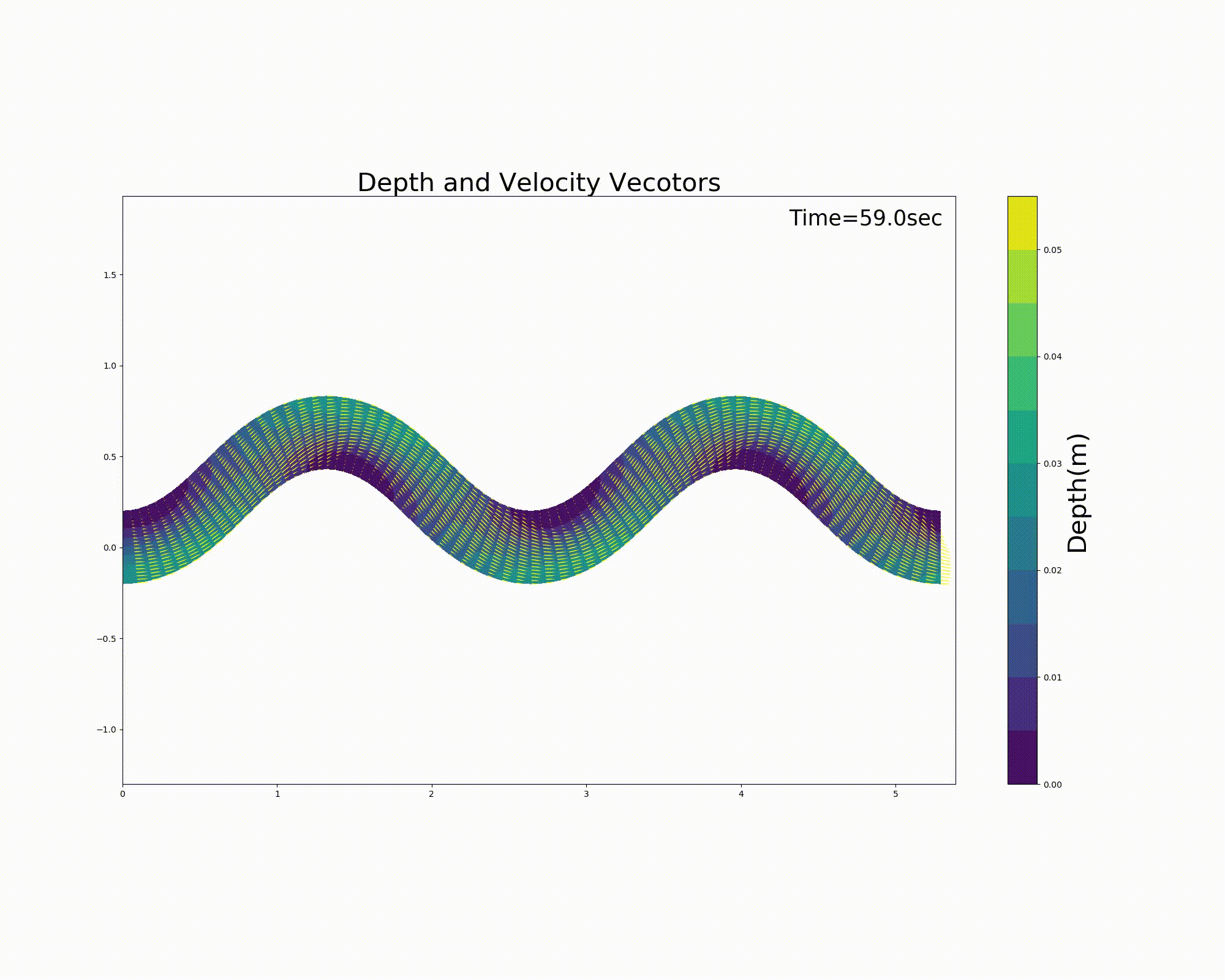
Figure 112 : Sin-Generated Curve水路における流れの計算結果(流速ベクトルと水深)

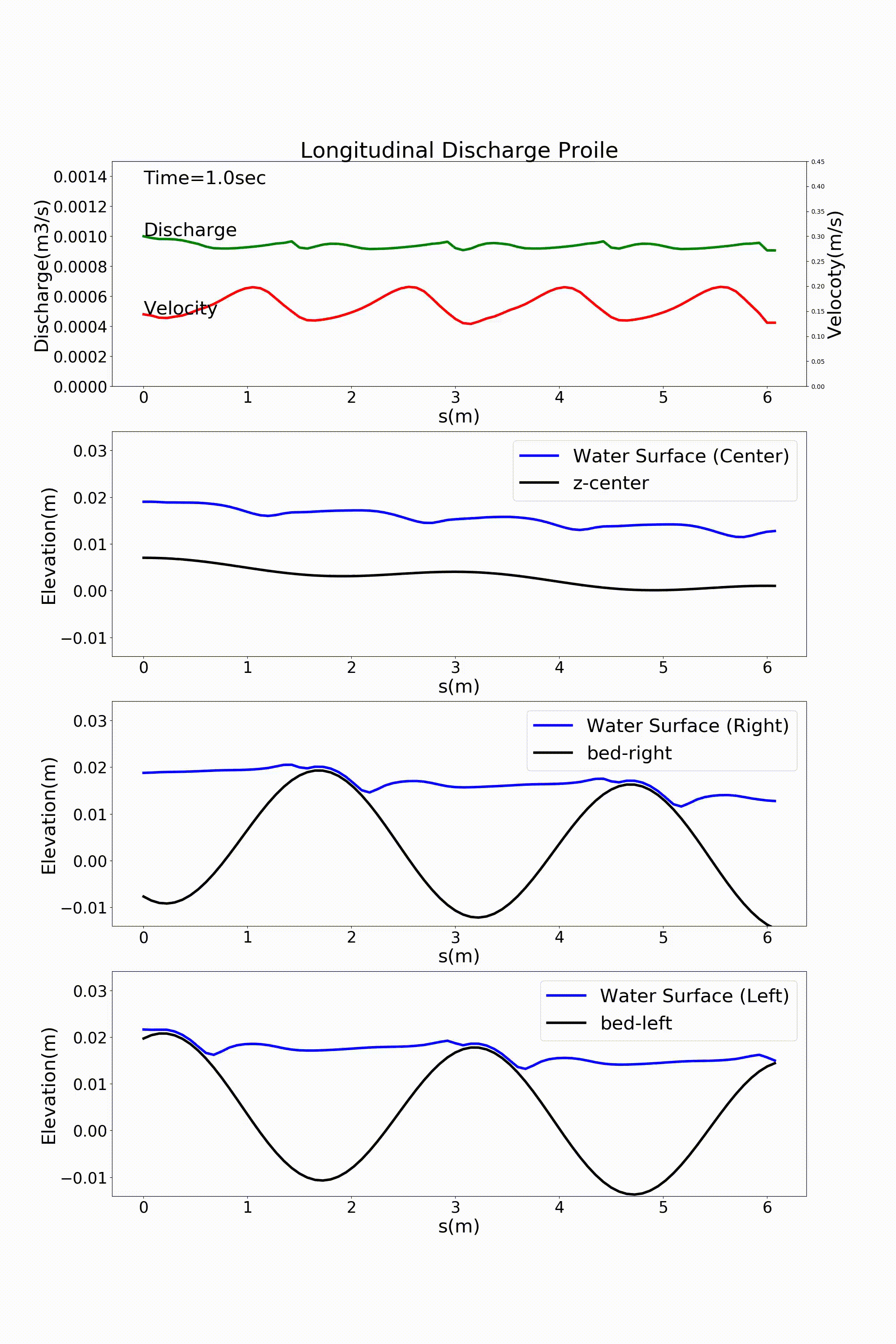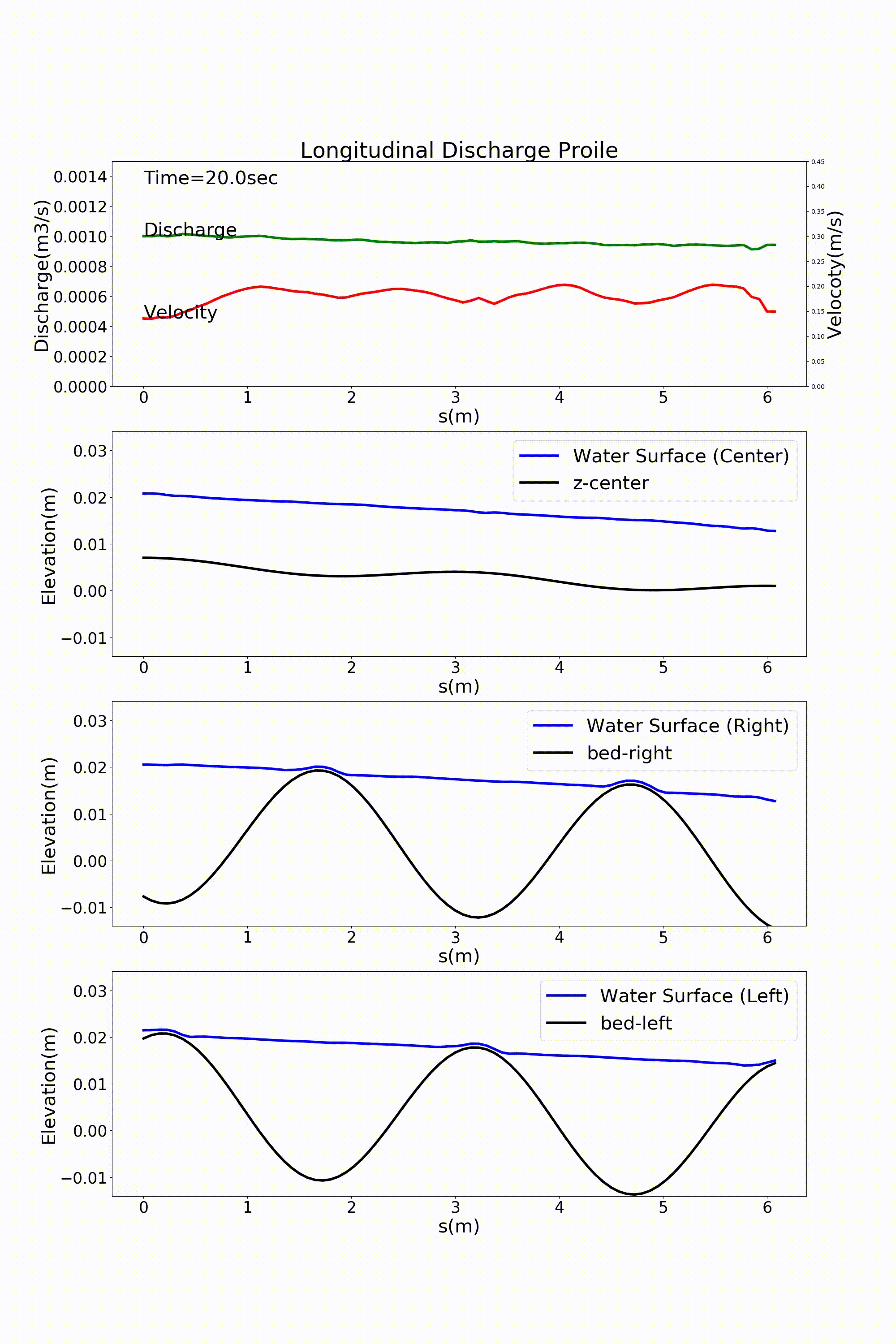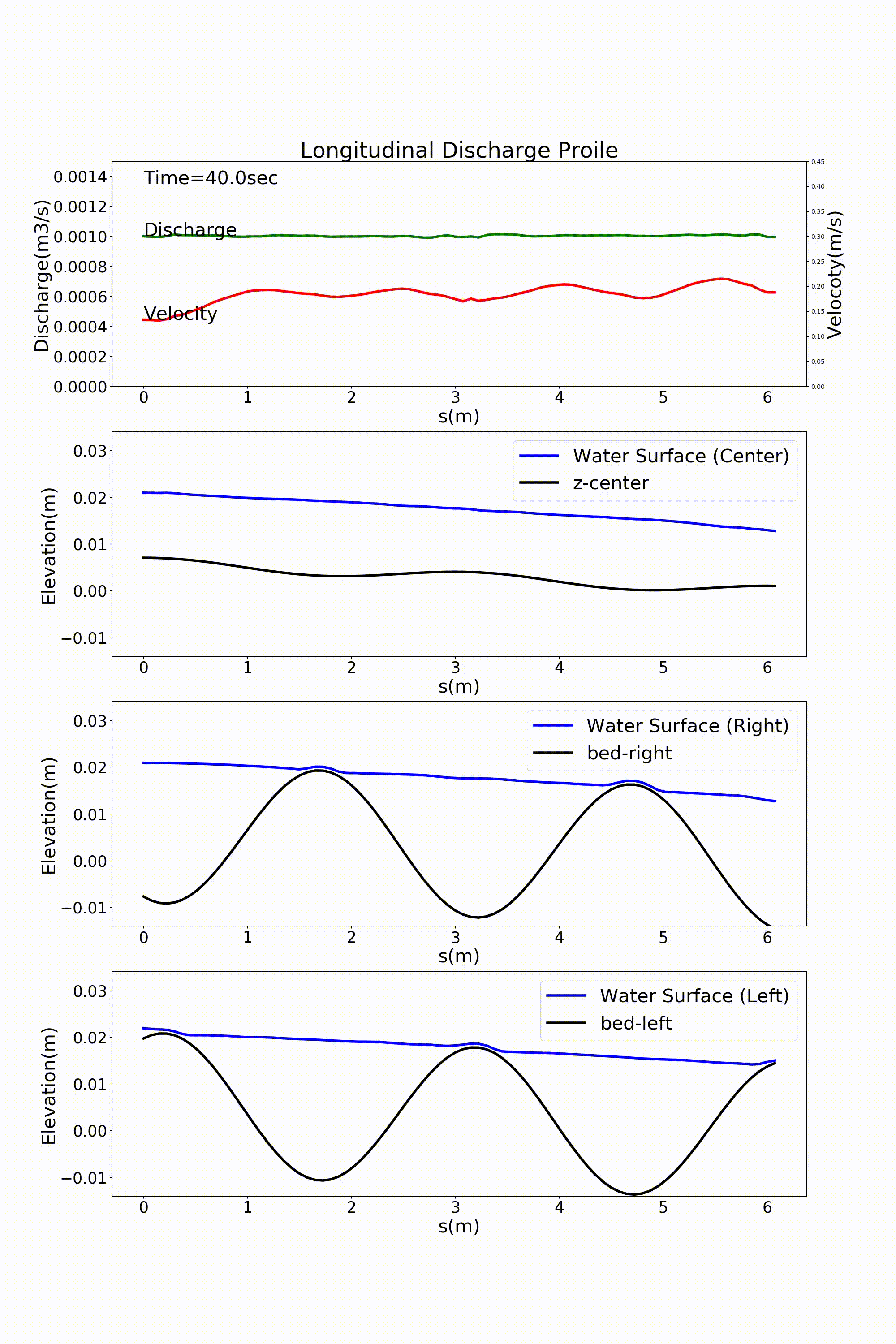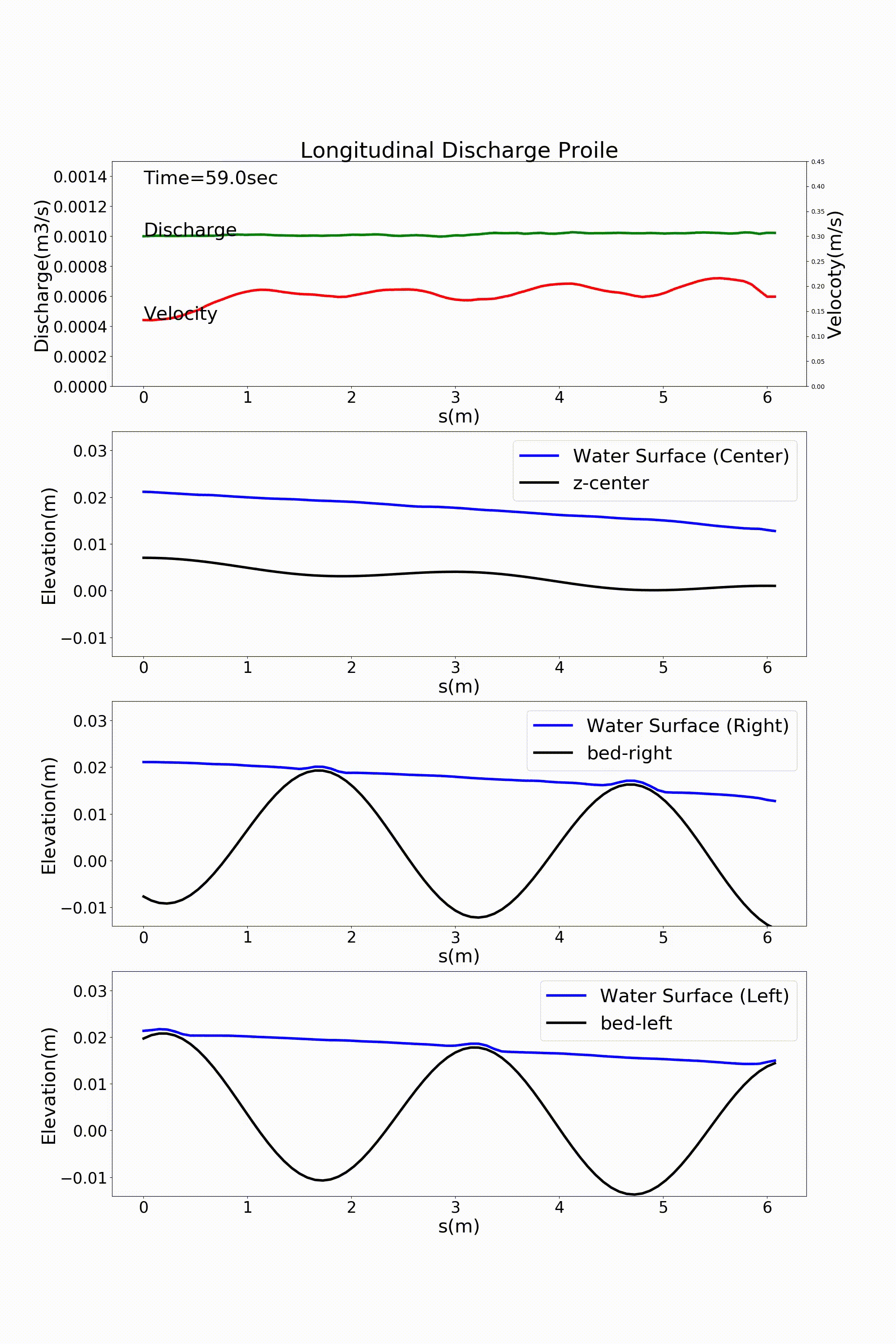
Figure 113 : Sin-Generated Curve水路における流れの計算結果(流量と水位縦断)

周期境界条件

通常，常流での計算は上流端で流量(流速), 下流端で水位(水深)を境界条件として与えます． Figure 112 および Figure 113 の計算も上流から一定の流量を与え, 下流端で一定の水位(この場合は等流水位)を与えています． この境界条件の与え方を計算点との関係で示したのが Figure 114 です.

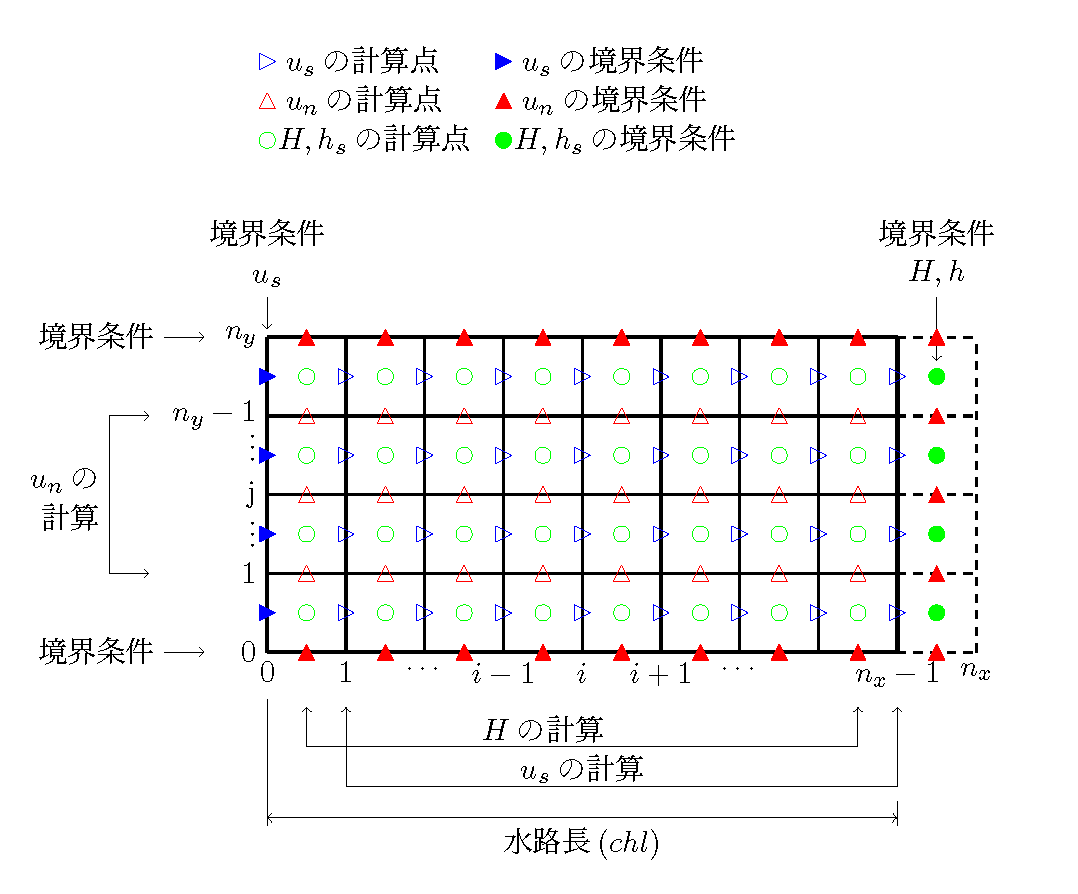
Figure 114 : 計算格子と境界条件(通常の計算の場合)

これに対して，例えば Sin-Generated Curveのような蛇行水路が無限に続くような状態を 想定する時に良く用いられるのが 周期境界条件 (Periodic Boundary Condition)と呼ばれる 境界条件の与え方で，これは，上流と下流の水理量を同じに保つことにより，無限に続く 水路を想定した計算を行う方法です．

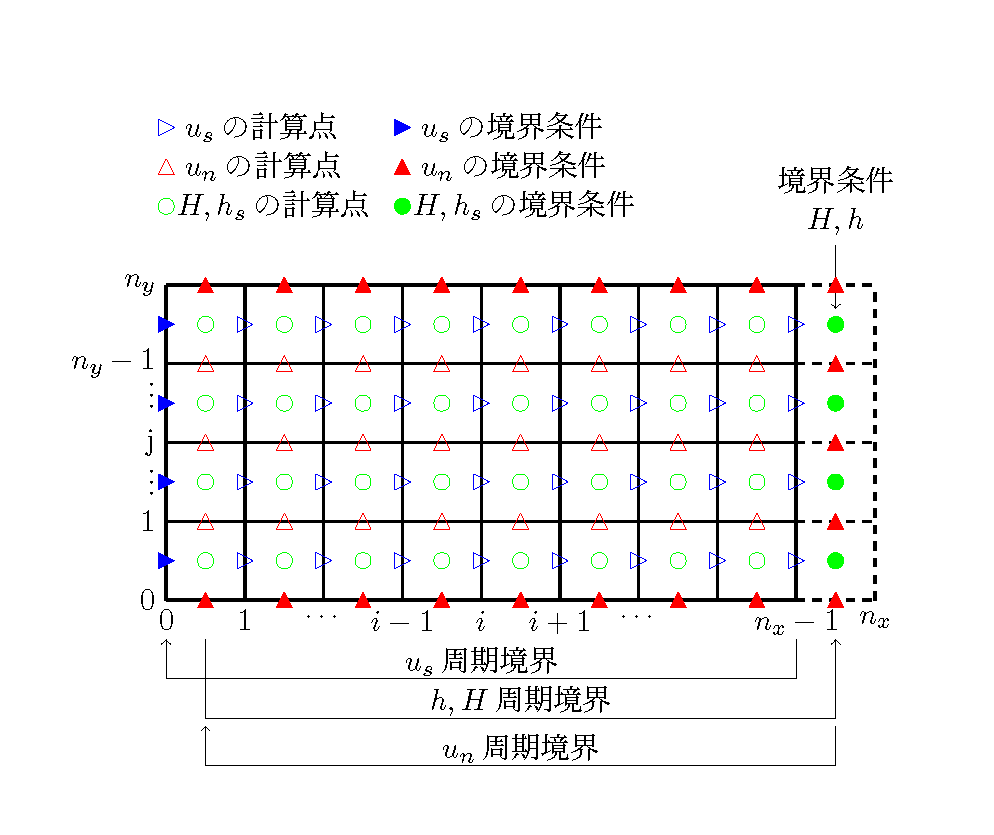
Figure 115 : 計算格子と境界条件(通常の計算の場合)

ちなみに， https://github.com/YasuShimizu/Nays2d_sn_python

にアップロードしてあるコードはこの周期境界条件にも対応してあり，計算条件を記述した config.ymlファイル　(https://github.com/YasuShimizu/Nays2d_sn_python/blob/main/config.yml) の第1行目:

j_rep: 1 # 周期境界条件 0:周期境界条件無 1:周期境界条件

の j_rep というパラメーターを1とすることによって周期境界条件を表現することが可能になります． Figure 116 および, Figure 117 は直前の :numref:`sg_animation および Figure 113 の計算結果を周期境界条件としたものです． 一見同じように見えますが，実は周期境界条件を適用しています．

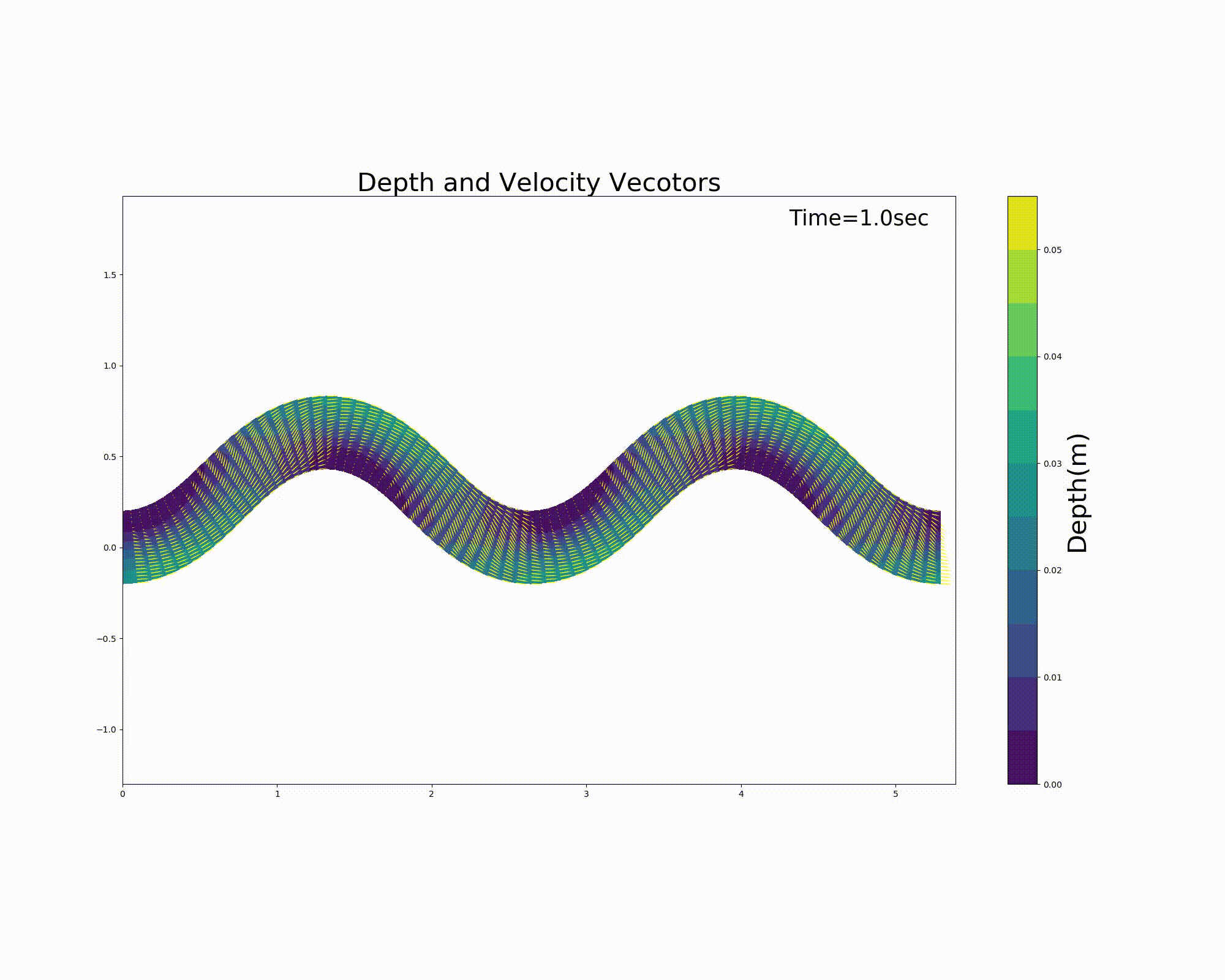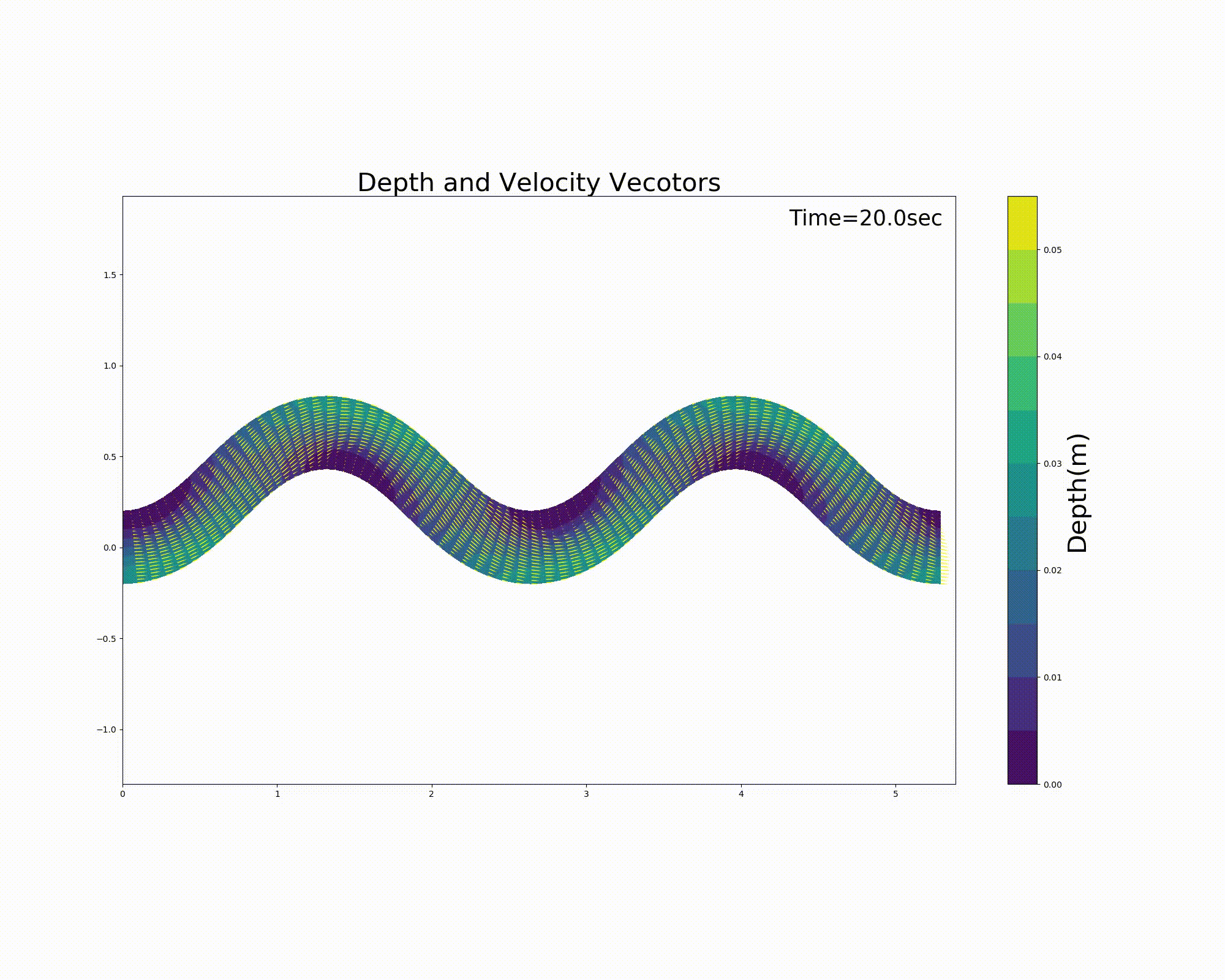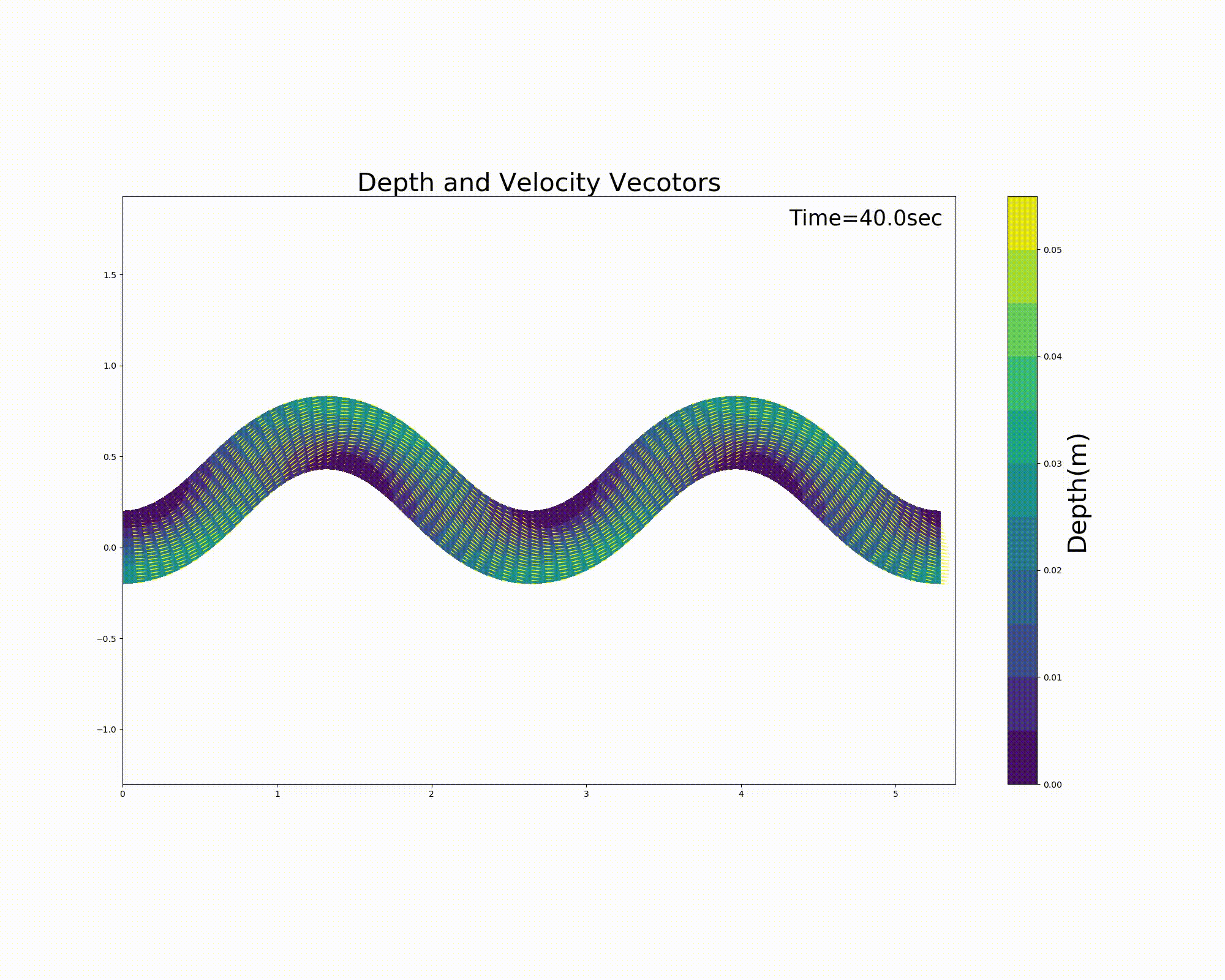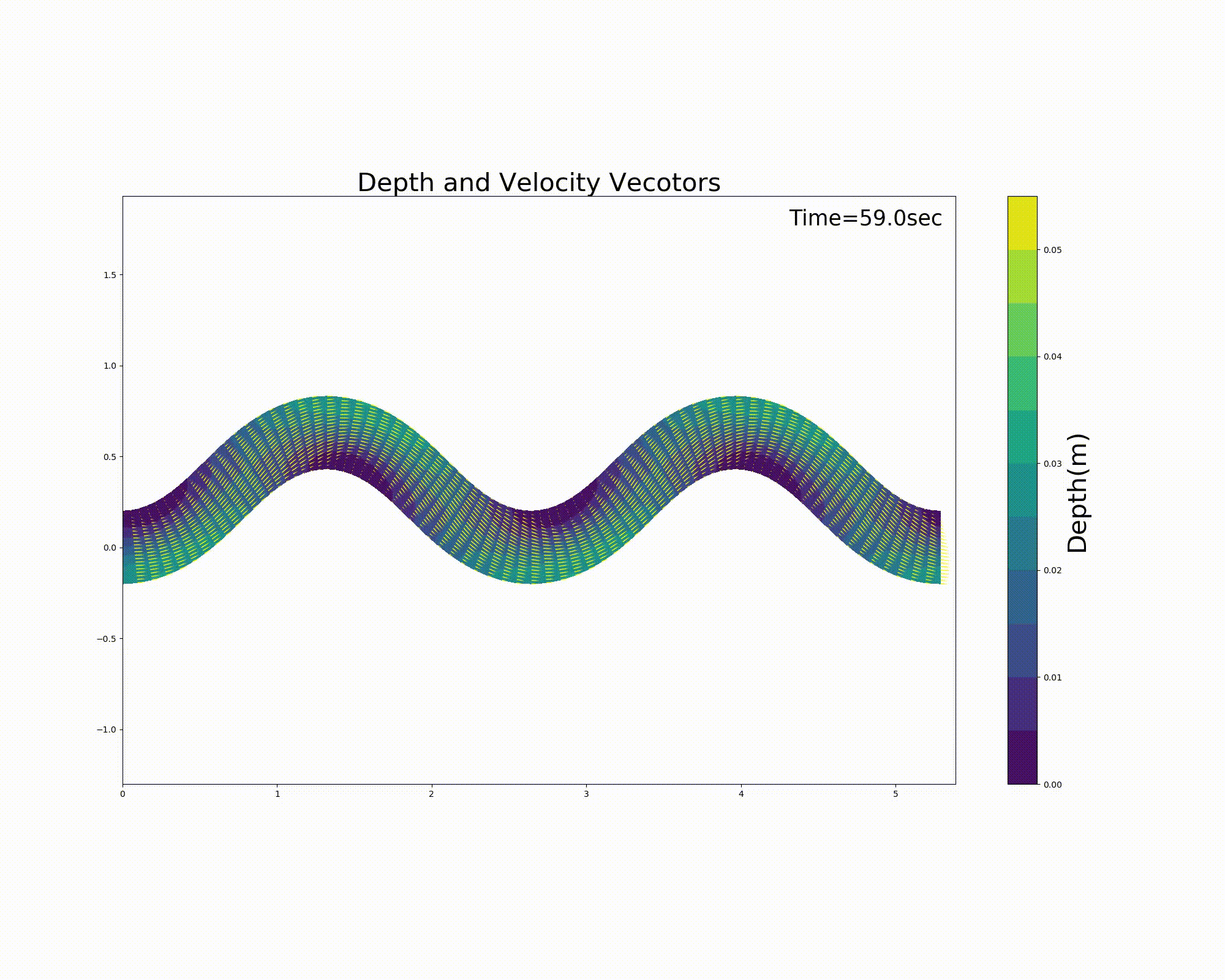
Figure 116 : Sin-Generated Curve水路における流れの計算結果(流速ベクトルと水深) [周期境界条件]

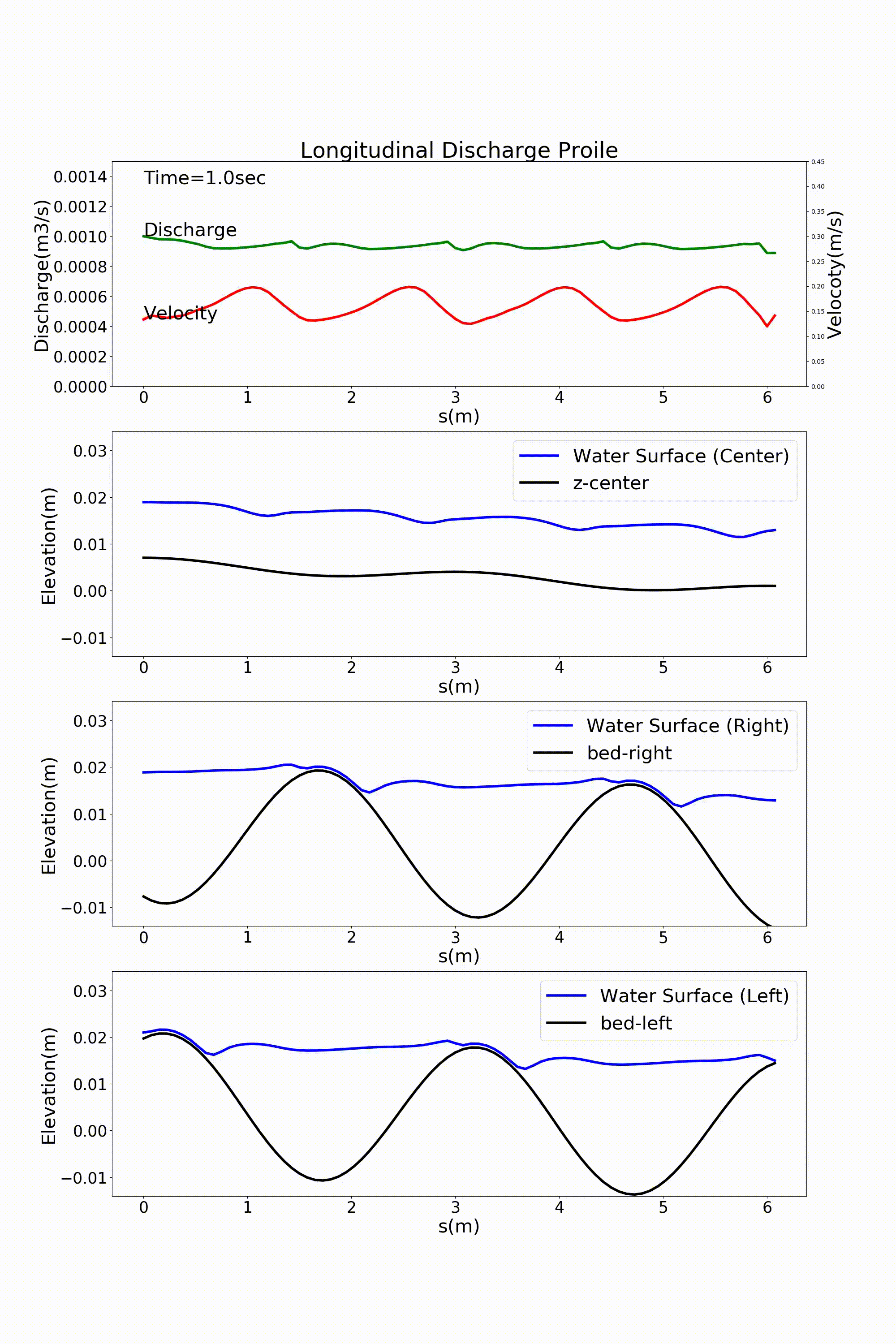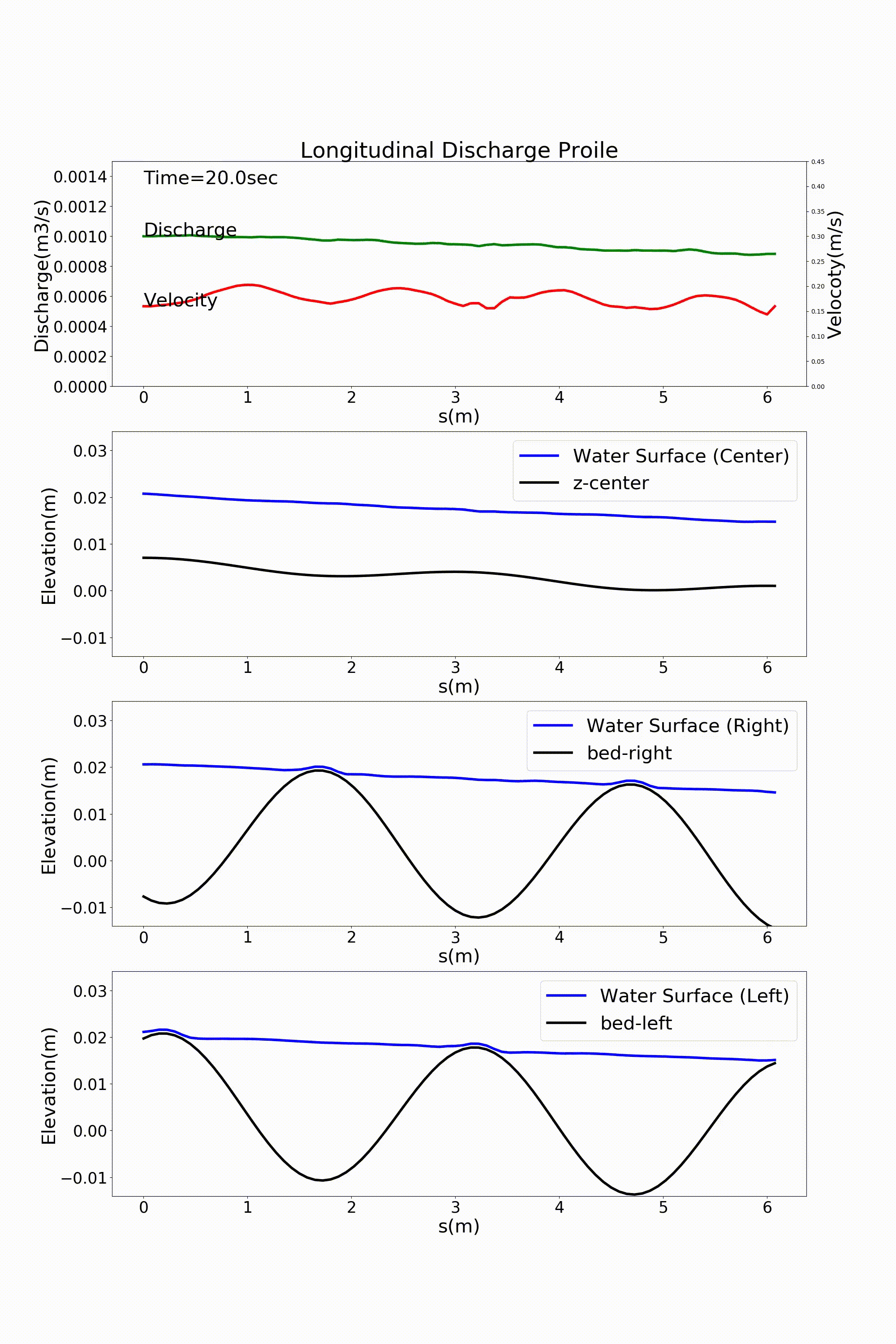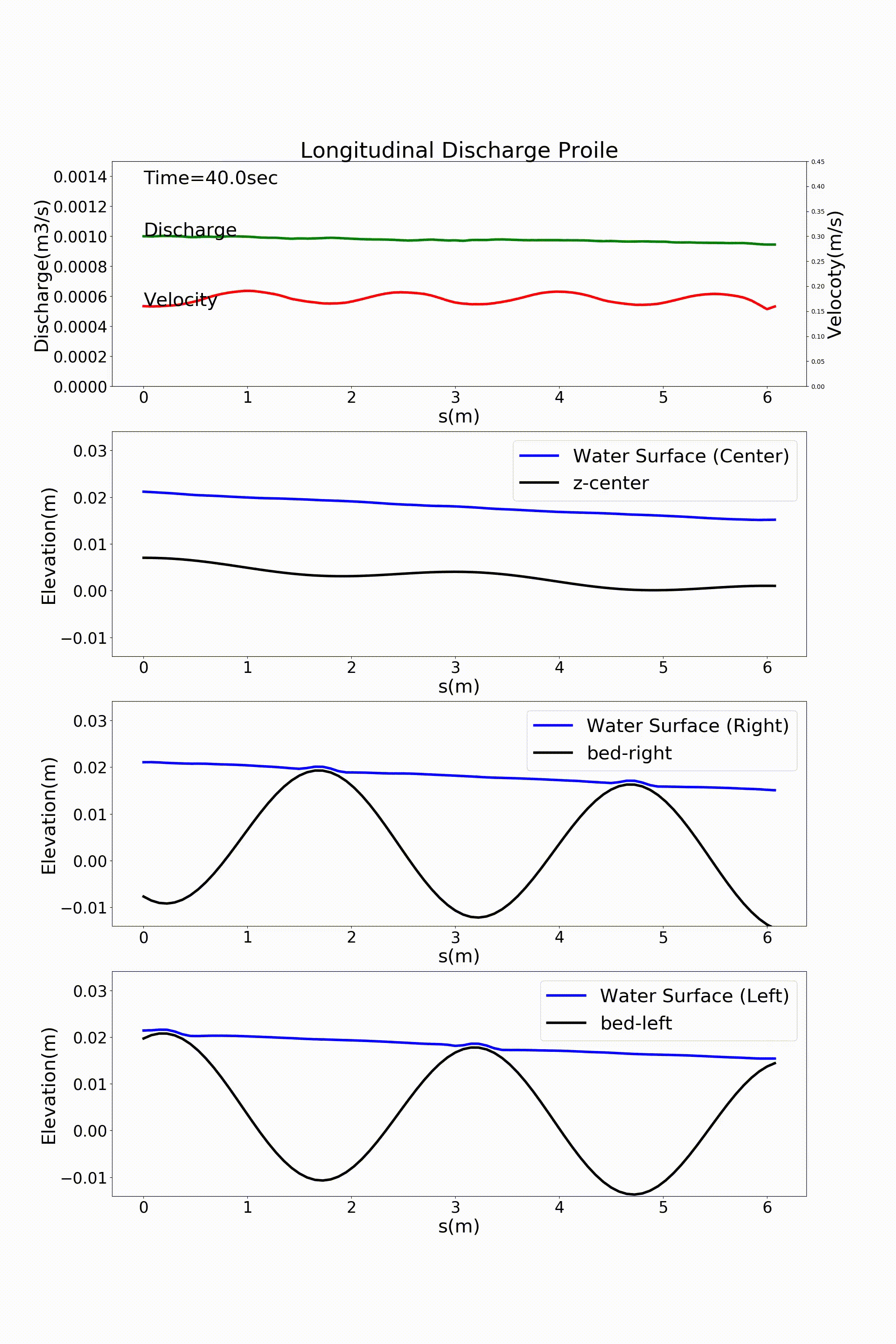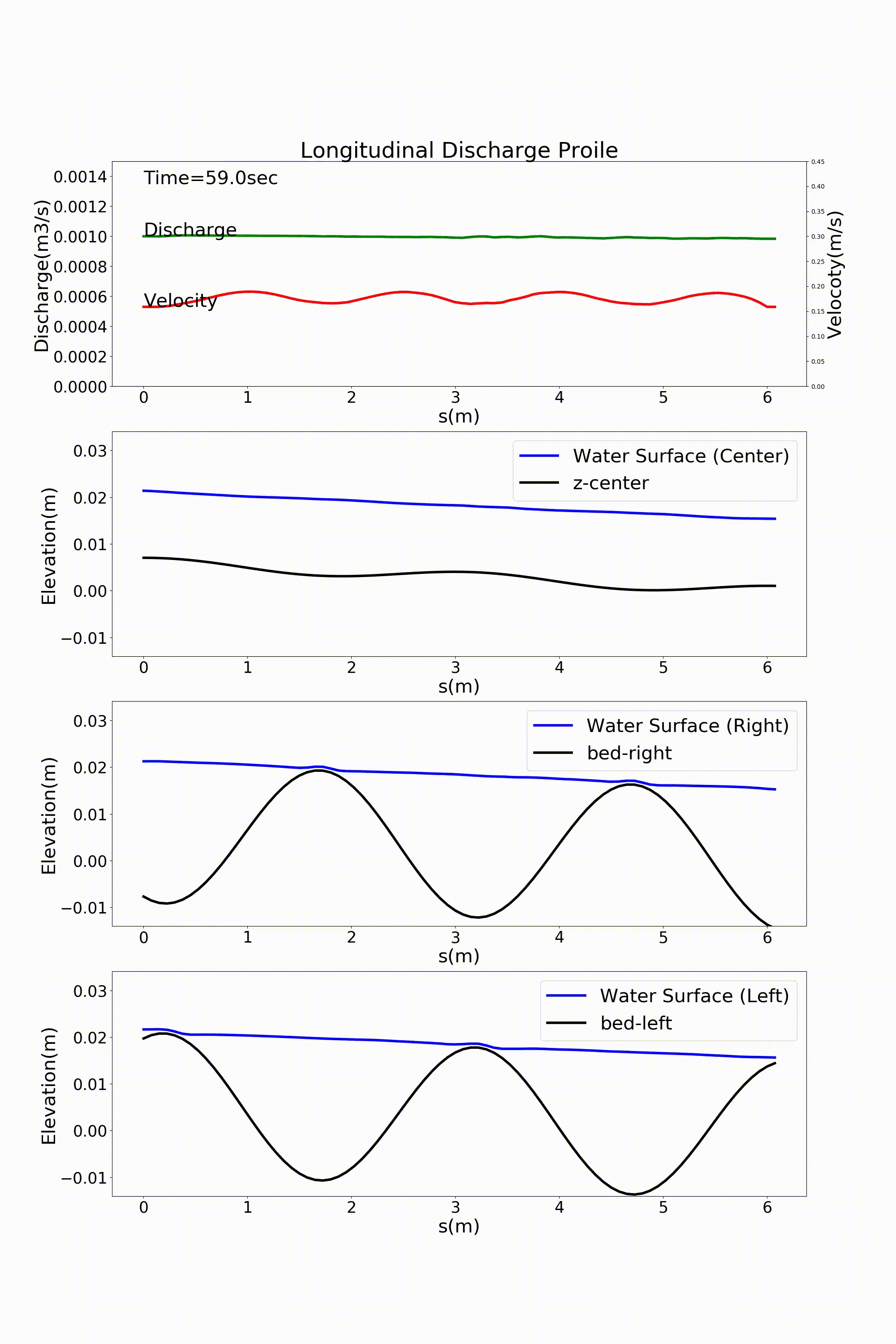
Figure 117 : Sin-Generated Curve水路における流れの計算結果(流量と水位縦断) [周期境界条件]