この節の作者: 清水康行 <yasu@i-ric.org>

本テキストへの感想, 質問, 要望, バグ報告などはこちらへお願いします.

蛇行河川流れの計算(基礎編)

Sin-Generated Curve (サインジェネレーテッド曲線)

Sin-Generated Curveの生成法

Langbein and Leopold [Ref:33] によれば蛇行河川の河道形状は次式のSine-Generated-Curveによって近似することが可能とされています. これは，河川の平面座標がサインカーブという訳ではなく，河道の向かう方向の角度がサイン関数で表されるという意味です．

(251)\[\theta = \theta_0 \sin \cfrac{2\pi s}{L}\]

ただし, \(s\) は河道中心線に沿った座標軸, \(\theta\) は \(s\) 軸の水平方向に 対する角度(蛇行偏角度), \(\theta_0\) は最大蛇行偏角, \(L\) 蛇行波長( \(s\) 軸に沿った長さ)です．Figure 73 , Figure 74 および Figure 75 は すべてこのSine-Generated-Curveによるシミュレーション結果です．

(251) 式による河道形状を図示する場合や，その形状を用いて解析を行う場合， その形状を \(x-y\) 座標に変換する必要があります．

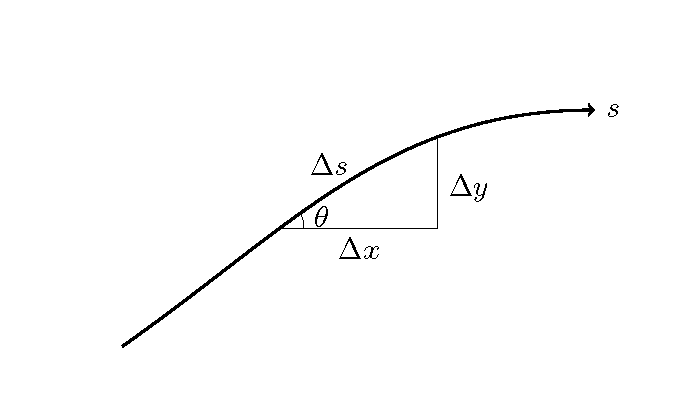
Figure 95 : \(\Delta x, \Delta y, \Delta s\) の関係

\(s\) 軸に沿った微小要素 \(\Delta s\) の \(x,y\) 方向成分は, Figure 95 より,

(252)\[\Delta x = \Delta s \cos\theta, \hspace{2cm} \Delta y = \Delta s \sin\theta\]

で定義されます．この結果，\(s,x,y\) は以下で求められます．

(253)\[s=s_0 +\int_{s_0}^s ds, \hspace{1cm} x=x_0 +\int_{s_0}^s \cos\theta ds, \hspace{1cm} y=y_0 +\int_{s_0}^s \sin\theta ds\]

実際の計算は,

1. 微小な \(\Delta s\) を \(s\) 軸に沿って逐次加算していき，

2. その都度 (251) 式で \(\theta\) を求め，

3. その \(\theta\) と上で定めた \(\Delta s\) で (252) 式で，\(\Delta x\) , \(\Delta y\) を求め,

4. これを累加することにより, \(x, y\) 座標値を逐次求めて行く．

という手順になります． これを，Pythonコードにしたのがこちらです． https://github.com/YasuShimizu/Python-Code/blob/main/sg_plot.py

このコードでは, \(\theta_0\) が \(30^\circ, 60^\circ, 90^\circ, 120^\circ\) の場合の4種類 Sine-Generated Curveの線形をプロットされています．波長，波数などはコード中で指定するようになっています．このコードを実行した結果が下図です．

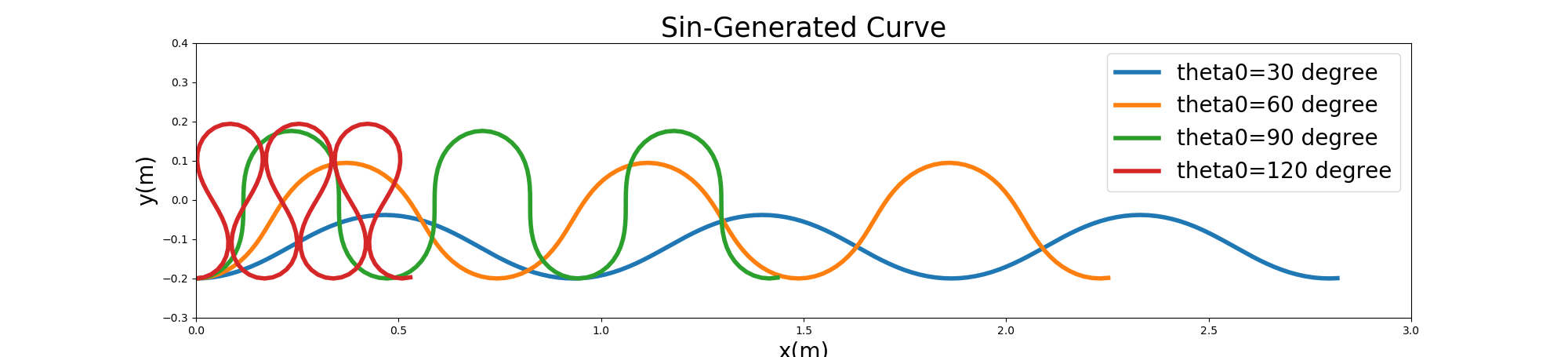
Figure 96 : Sin-Generated Curveの例

Sin-Generated Curveを用いた計算格子の作成

Figure 96 で示した形状は河道中心線の形状で，実際に2次元の解析を行う場合には 左右岸の河岸の座標およびこれを横断方向の格子数で分割した各格子の座標が必要になります．

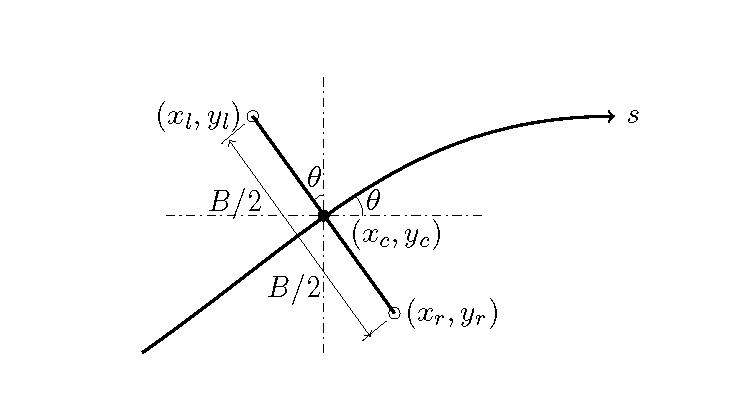
Figure 97 : Sin-Generated Curve における左右河岸の関係

Figure 97 に示すように, 河道中心線である \(s\) 軸に直交する横断線上に， 左右に河幅の半分の距離にある2点が左右岸の座標となります． 河道中心および左右岸の格子点の座標を \((x_c, y_c), (x_r, y_r), (x_l, y_l)\) とすると，次式が成立します．

(254)\[ \begin{align}\begin{aligned}x_r=x_c+\cfrac{B}{2}\sin\theta, \hspace{2cm} & y_r=y_c-\cfrac{B}{2}\cos\theta\\x_l=x_c-\cfrac{B}{2}\sin\theta, \hspace{2cm} & y_l=y_c+\cfrac{B}{2}\cos\theta\end{aligned}\end{align} \]

計算格子はこの左右岸の座標を所定の格子数で分割したものになります．

以下は \(\theta_0=40^\circ\) の例で,

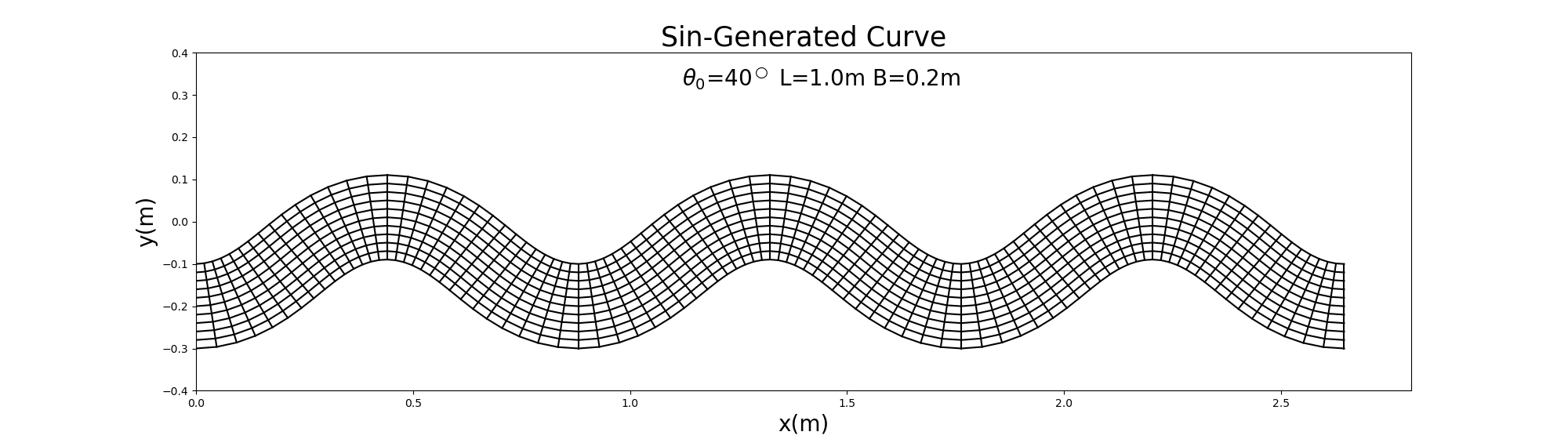
Figure 98 : \(\theta=40^\circ\) のSin-Generated Curve計算格子

この格子生成用のPythonコードはこちらです．

https://github.com/YasuShimizu/Python-Code/blob/main/sg_mkgrid40.py

ちなみに, \(\theta_0=100^\circ\) の例はこちらです.

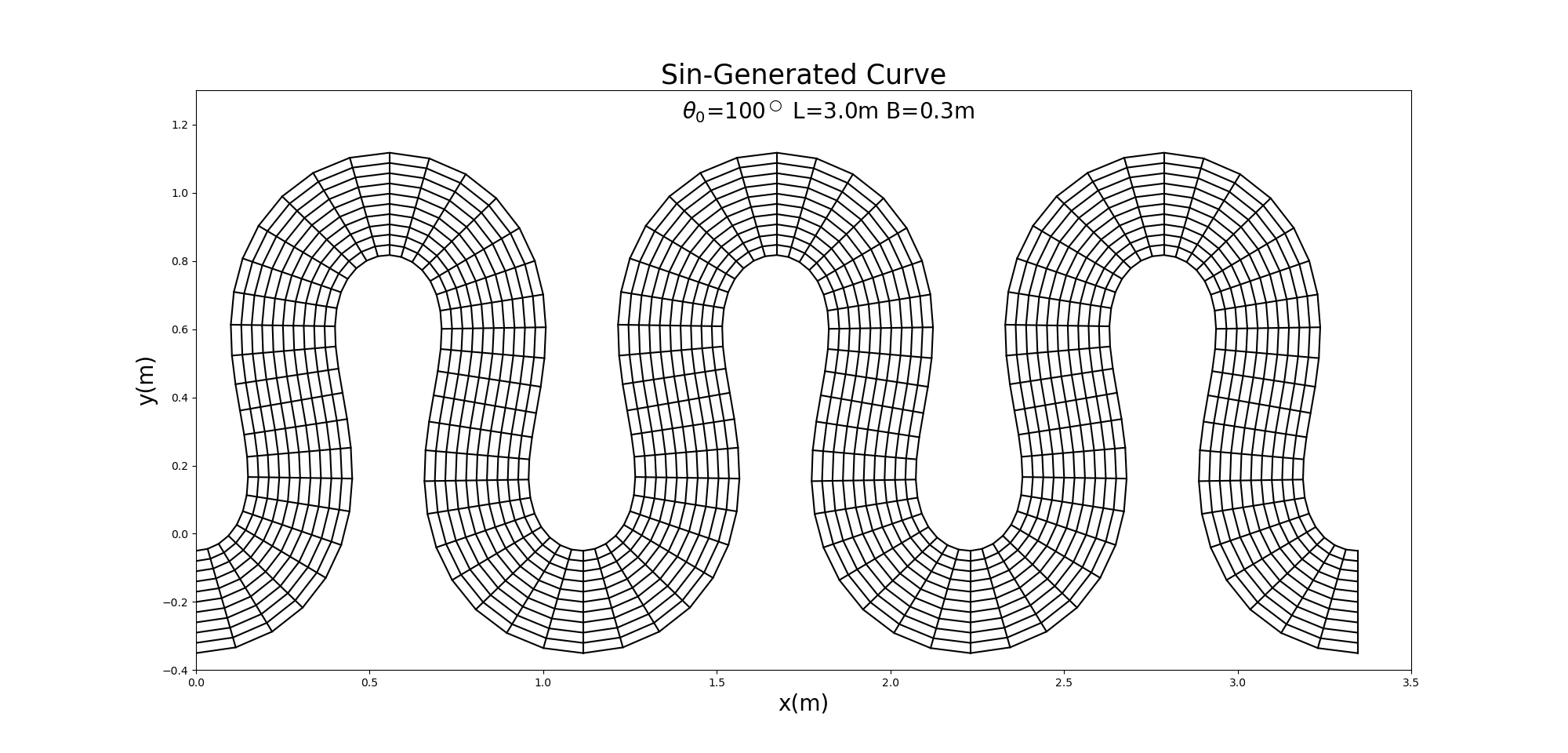
Figure 99 : \(\theta=100^\circ\) のSin-Generated Curve計算格子

Pythonコードはこちらです．

https://github.com/YasuShimizu/Python-Code/blob/main/sg_mkgrid100.py

河床に砂州状の形状を与える

生成された計算格子 Figure 99 の平面形状に次式で河床に砂州状の比高を与えることが出来ます．

(255)\[\Delta_z = -A_p\cos\left\{\cfrac{2\pi}{L}(s-\delta_s)\right\} \cos\left\{\cfrac{\pi}{B}n\right\}\]

ただし, \(\Delta_z\) 河床からの比高，\(A_p\) は砂州波高, \(s\) は上流端から下流に向かった河道中心線上の距離, \(n\) は右岸から 左岸に向かった距離, \(\delta s\) は砂州と河道形状の位相差です．

(255) 式を用いて砂州形状の比高を Sine-Generated Curve水路上に 配置した結果は下記となります．なお, この例では, \(\theta_0=100^\circ\), \(L=\) 3.0m, \(B=\) 0.3m, \(A_p=\) 0.03m, \(\delta_s=\) 0.1m となっています．

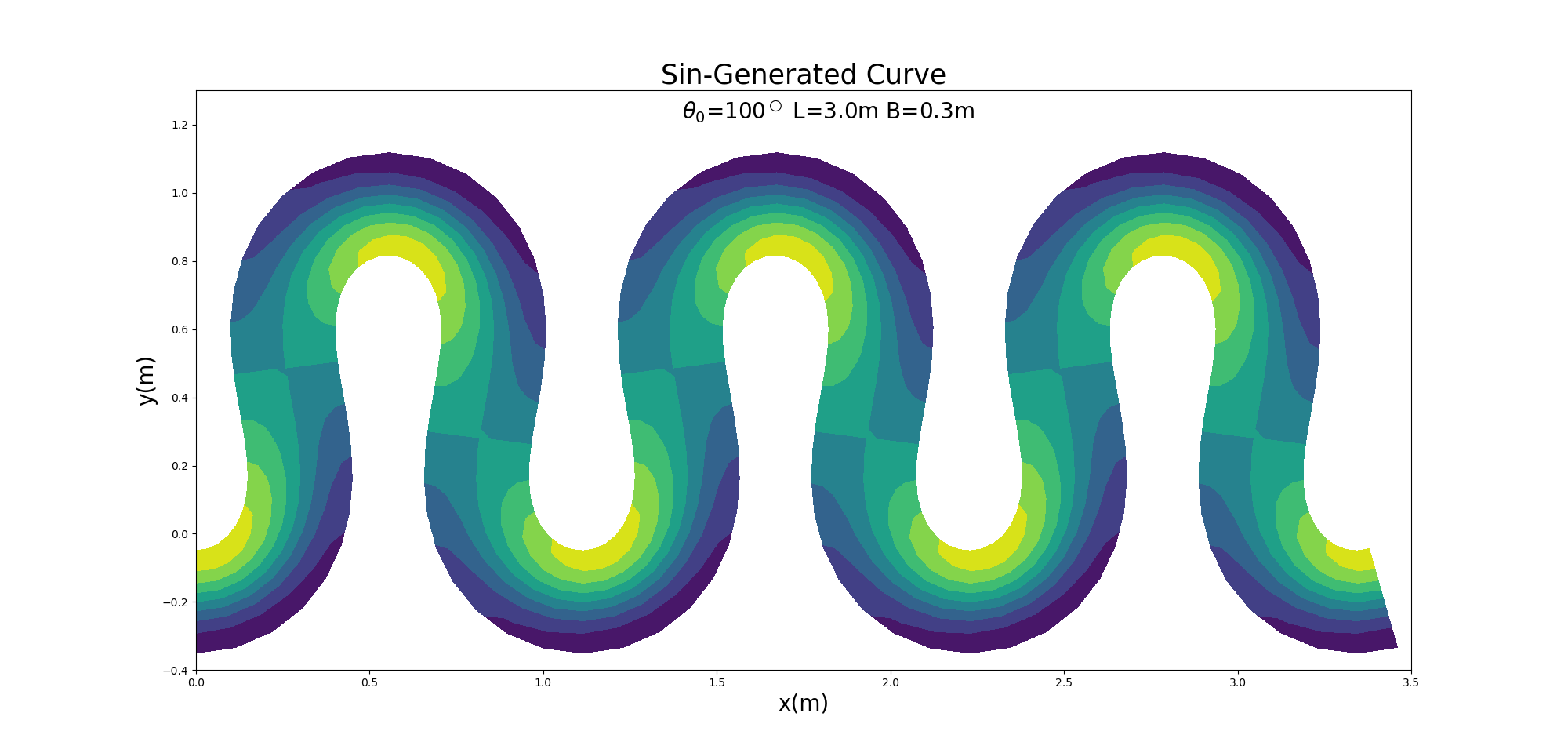
Figure 100 : \(\theta=100^\circ\) のSin-Generated Curve上の砂州状河床

Figure 100 の計算および作図のためのPythonコードはこちらです．

https://github.com/YasuShimizu/Python-Code/blob/main/sg_mkgrid_dz.py

Kinoshita-generated Meander Curve (木下蛇行曲線)

Abad and Garcia [Ref:34] によれば，(251) 式に次式で表されるような付加項を付け加えることにより，Figure 101 のような自然河川の蛇行形状を表現可能であるとされています．

(256)\[\theta = \theta_0 \sin \cfrac{2\pi s}{L} +{\theta_0}^3\left\{J_s \cos\left(3\cfrac{2\pi s}{L}\right) -J_f \sin\left(3\cfrac{2\pi s}{L}\right) \right\}\]

ここで, \(J_s\) および \(J_n\) はそれぞれSkewness(歪度)およびflatness(扁平度)を表す係数です．

Figure 101 : 米国アラスカ州のAlatna川 [Ref:35]

(256) 式において, \(\theta_0=100^\circ\), \(L\) =2.8m, \(B\) =0.2m, \(J_s=1/32, J_f=1/192\) として作成した水路計算格子を Figure 102 に示します．Abad and Garcia [Ref:34] はこのような形の平面形状を木下 [Ref:24] による迂曲河道にちなんで, Kinoshita-generated Meander Curve（木下蛇行曲線)と呼んでいます．

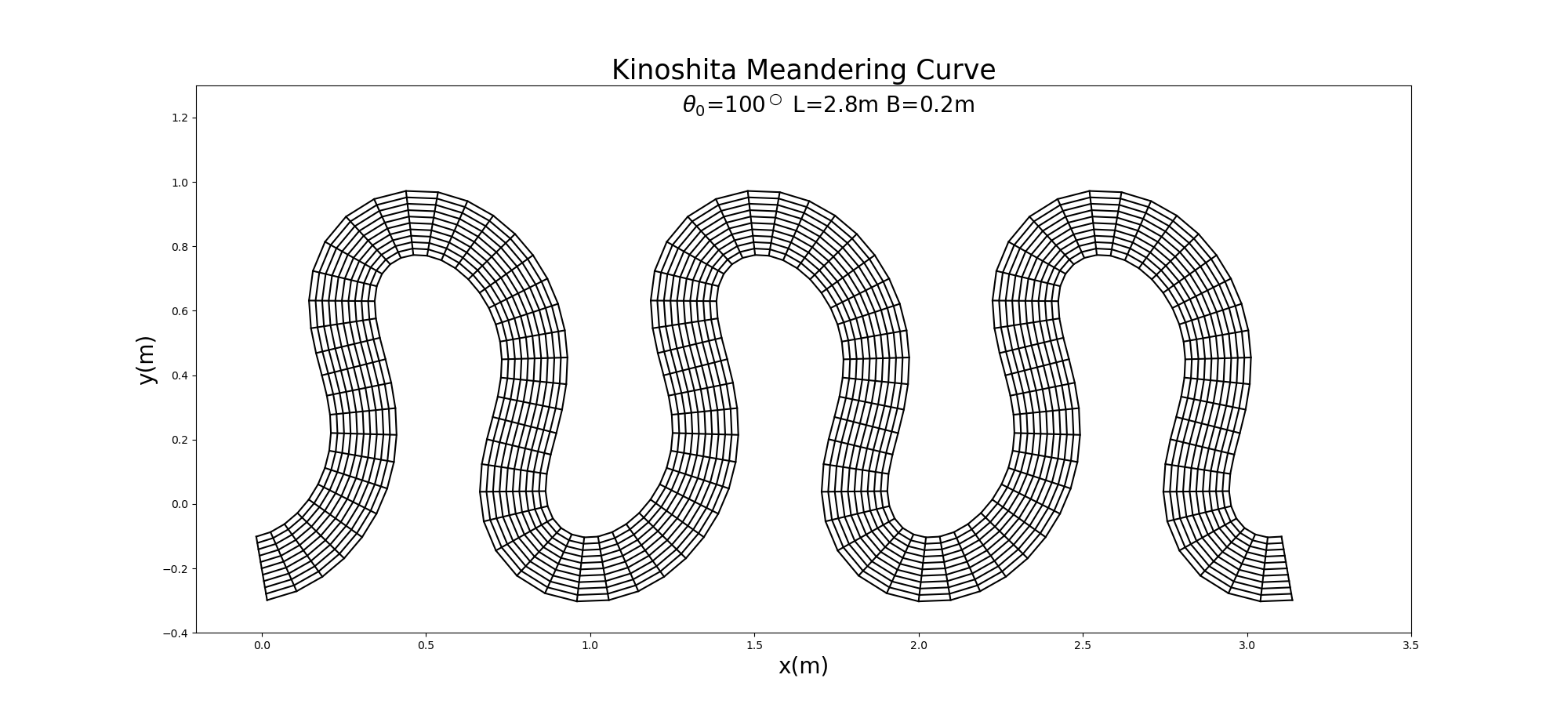
Figure 102 : 木下蛇行曲線水路

Figure 102 の計算格子を生成し作図するPythonコードはこちらです．

https://github.com/YasuShimizu/Python-Code/blob/main/kinoshita100.py

Figure 102 の木下蛇行水路においても (256) 式の砂州上比高を与えることにより， 実河川の砂州形状を模した河床地形とすることが出来ます．

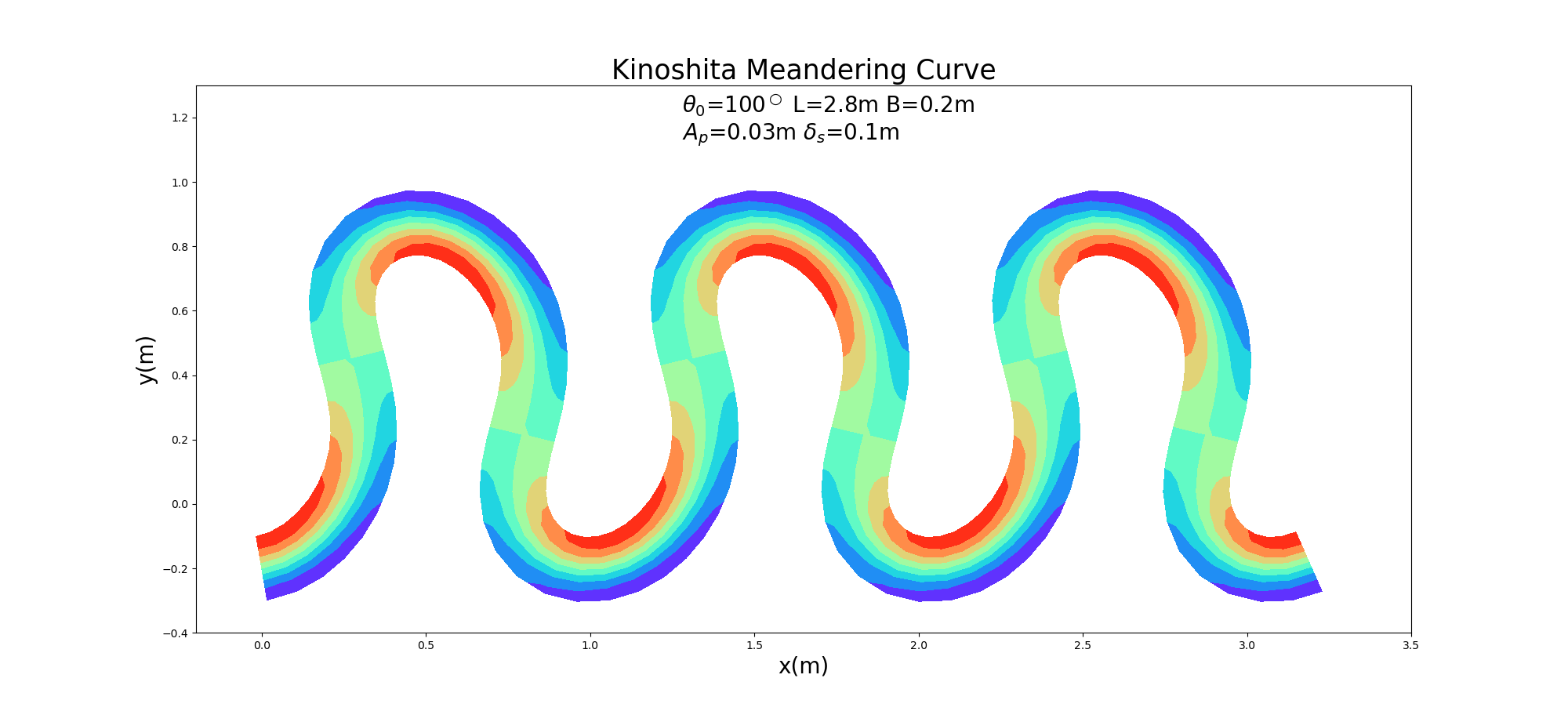
Figure 103 : \(\theta=100^\circ\) \(A_p=\) 0.03m, \(\delta_s=\) 0.1m のKinoshita-Generated Curve上の砂州状河床

Figure 103 の作図用Pythonコードを下記に示します．

https://github.com/YasuShimizu/Python-Code/blob/main/kinoshita100_dz.py

曲率の算定法

上記Sin-Generated CurveやKinoshita-Generated Curveの場合，流路の曲率は

(257)\[\cfrac{1}{r}= \cfrac{\partial \theta}{\partial s}\]

で, 算定出来ます．例えば，(251) 式のSin-Generated Curveの場合,

(258)\[\cfrac{1}{r}=\cfrac{\partial \theta}{\partial s} = \cfrac{2\pi}{L}\theta_0 \cos \cfrac{2\pi n}{L}\]

となります．ただし，一般に河川の形状は上記のような関数形に完全に一致することはなく， 自然河川でも人工的な河川でも様々な任意形状から求めることになります．

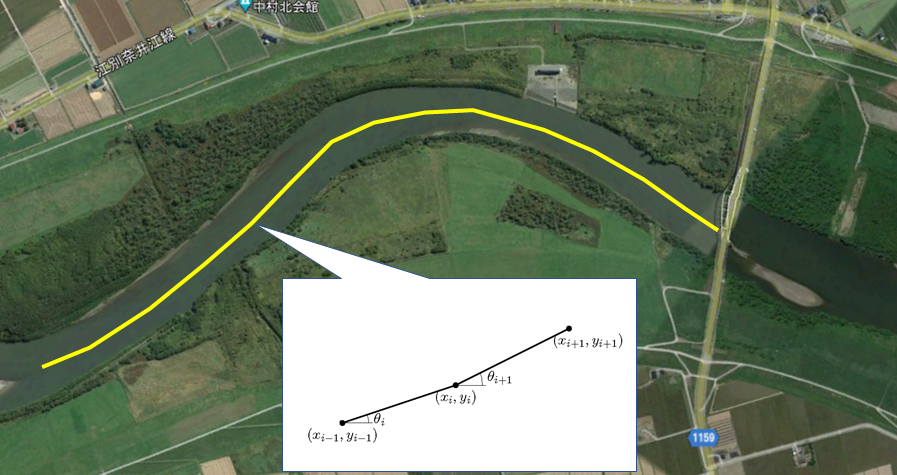
Figure 104 : 平面座標から曲率半径を算定する

Figure 104 に示すような河道中心に沿った平面座標がある場合にも， (257) 式を離散的に用いることで曲率半径を求めることが出来ます． 今，

(259)\[\cfrac{d}{ds}\left(\cfrac{dy}{dx}\right)=\cfrac{d}{ds}\tan\theta =\cfrac{1}{\cos^2\theta}\cfrac{d\theta}{ds}\]

なので,

(260)\[\cfrac{1}{r}=\cos^2\theta\cfrac{d}{ds} \left(\cfrac{dy}{dx}\right)\]

Figure 104 に示す記号を用いて,

(261)\[\begin{split}\Delta x_i=x_i-x_{i-1}, \hspace{1cm} \Delta y_i=y_i-y_{i-1}, \hspace{1cm} \Delta s_i =\sqrt{\Delta x_x^2 + \Delta y_i^2} \\ \cos\theta_i = \cfrac{\Delta x_i}{\Delta s_i}, \hspace{4cm} \sin\theta_i = \cfrac{\Delta y_i}{\Delta s_i} \hspace{3cm}\end{split}\]

などの定義を行いますと,

(262)\[ \begin{align}\begin{aligned}\cfrac{1}{r}=\cos^2\theta \cfrac{d}{ds}\left(\cfrac{dy}{dx}\right) =\cfrac{\Delta x^2}{\Delta s^2} \cfrac{\Delta x \cfrac{d(\Delta y)}{ds}-\Delta y \cfrac{d(\Delta x)}{ds}}{\Delta x^2}\\=\cfrac{1}{{\Delta s_i}^2} \left[ \Delta x \left\{ \sin\theta_{i+1}-\sin\theta_i \right\} -\Delta y \left\{ \cos\theta_{i+1} - \cos\theta_i \right\} \right]\\=\cfrac{1}{\Delta s_i} \left[ \cos\theta_i \left\{\sin\theta_{i+1}-\sin\theta_i \right\} -\sin\theta_i \left\{ \cos\theta_{i+1} - \cos\theta_i \right\} \right]\end{aligned}\end{align} \]

試しに，Sine-Generated Curveにおいて, (258) を用いて解析的に算出した 曲率と, (262) 式を使って数値的に算出して曲率を比較した結果を下図に示します． 解析解が青線で，数値解がオレンジ線です. この例は蛇行偏角 \(\theta_0=90^\circ\) の場合ですが，両者がほとんど完全に一致しているのが分かります．

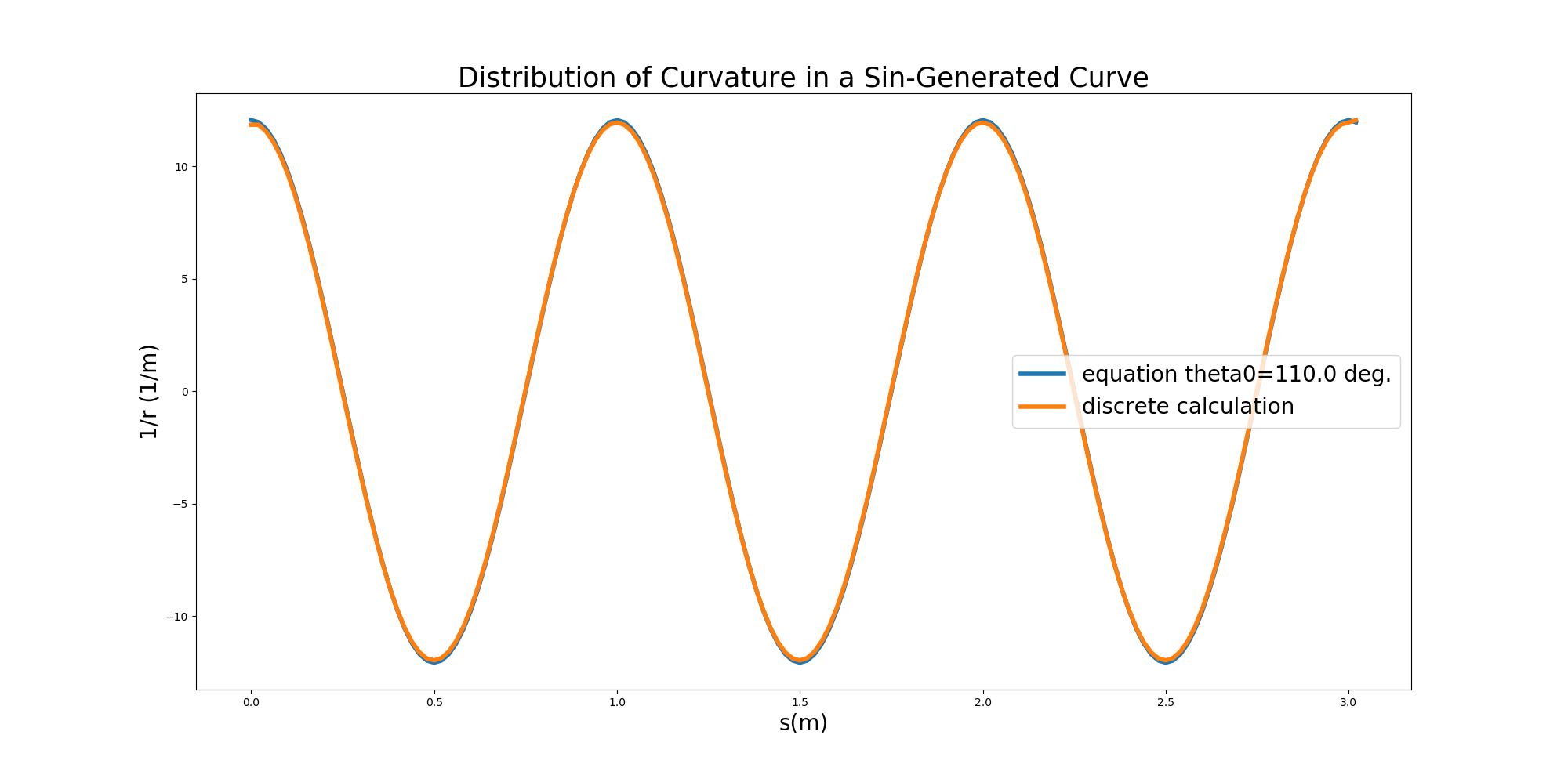
Figure 105 : 数値計算で曲率を算定する方法の検証例

Figure 105 の計算および作図のPythonコードは下記です．

https://github.com/YasuShimizu/Python-Code/blob/main/radius_cmp.py