この節の作者: 清水康行 <yasu@i-ric.org>

1次元非定常流(幅が一定の場合)¶

基礎式¶

水路幅一定, 長方形断面水路における非定常流れの連続式および運動方程式を以下で表します.

(71)¶\[{{\partial h}\over{\partial t}} +{{\partial (uh)}\over{\partial x}} = 0\]

(72)¶\[{{\partial (uh)}\over{\partial t}} +{{\partial (u^2 h)}\over{\partial x}} = -gh{{\partial H}\over{\partial x}} + \cfrac{\partial}{\partial x} \left\{ \varepsilon \cfrac{\partial (uh)}{\partial x} \right\} -{{\tau_x}\over{\rho}}\]

ここで, \(t\) は時間, \(x\) は流下方向距離, \(h\) は水深, \(u\) は流速, \(g\) は重力加速度, \(H\) は水位 \((=z_b+h)\), \(z_b\) は河床高, \(\varepsilon\) は渦動粘性係数, \(\tau_x\) は河床せん断力, \(\rho\) は水の密度です.

(72) 式の左辺は保存形と呼ばれる形で表現されており, 水面形が不連続の場合にも適用可能な形式となっています. 水面形が連続な場合, 即ち, \(\displaystyle{{\partial h}\over{\partial x}}\) や \(\displaystyle{{\partial u}\over{\partial x}}\) が存在する場合には (72) 式の左辺は,

(73)¶\[u{{\partial h}\over{\partial t}} +h{{\partial u}\over{\partial t}} + u{{\partial(uh)}\over{\partial x}} +uh{{\partial u}\over{\partial x}}\]

と展開可能となり, (71) 式の連続式を用いることにより, (72) 式は次式となります. ただし, 拡散項は近似的な表現です.

(74)¶\[{{\partial u}\over{\partial t}} +u{{\partial u}\over{\partial x}} = -g{{\partial H}\over{\partial x}} + \varepsilon {{\partial^2 u}\over{\partial x^2}}-{{\tau_x}\over{\rho h}}\]

以下の説明では, 運動方程式としてこの非保存形の (74) 式を用います. 本来は, 非保存形では不連続な流れは扱えないはずなのですが, CIP法を用いるとこの式でも不連続な流れにある程度対応可能なことが知られています. おそらく，CIP法で使用している3次式の補完関数が，関数の急変点にもある程度まで対応可能であることによるものと考えられます．

CIP法の適用の準備(分離解法)¶

議論をさらに単純化するために, 河床せん断力(摩擦)が無視でき, 粘性も無視できる場合を考えます. 基礎式は,

(75)¶\[{{\partial h}\over{\partial t}} +{{\partial (uh)}\over{\partial x}} = 0\]

(76)¶\[{{\partial u}\over{\partial t}} +u{{\partial u}\over{\partial x}} = -g{{\partial H}\over{\partial x}}\]

ということになります. 式を見て分かると思いますが今までは (52) 式のように未知変数が \(f\) のみであったものが, 今回は \(h\) と \(u\) の 2つになっているのが大きな違いです. 時間微分項から直感的に分かると思いますが, (75) 式で \(h\) を, (76) 式で \(u\) を計算します. (76) 式に (52) 式でやったように分離解法を適用します. 即ち,

(77)¶\[{{\partial u}\over{\partial t}} = -g \displaystyle{\left( {{\partial h}\over{\partial x}} + {{\partial z_b}\over{\partial x}} \right) }\]

(78)¶\[{{\partial u}\over{\partial t}}+u{{\partial u}\over{\partial x}} = 0\]

と分離します. ただし, \(H=h+z_b\) の関係を用いてあります. (76) 式で, \(u^n \rightarrow u^{n+1}\) を計算するのを, 中間に \(\widetilde{u}\) を設け, (77) 式で \(u^n \rightarrow \widetilde{u}\) を, (78) 式で \(\widetilde{u} \rightarrow u^{n+1}\) を計算します. なお (77) 式には \(h\) が含まれているため, (77) 式を計算する際に, (75) 式を同時に満たす必要があります. これを \(h^n \rightarrow \widetilde{h}\) と表しておきます. なお (78) 式のほうには \(h\) が含まれませんので, (75) 式と関連付けようがありませんので, \(h^{n+1}\) は (75) 式と (77) 式を連立して出てくる \(\widetilde{h}\) をそのまま用いて,

(79)¶\[h^{n+1}=\widetilde{h}\]

とすることにします. 以上を整理しますと下表のようになります．

Table 3 1次元非定常流れの分離解法¶
Phase名	\(u\) と \(h\) の更新	使用する式
[A] Non-advection Phase	\(u^n \rightarrow \widetilde{u}, h^n \rightarrow \widetilde{h}\)	(77) 式, (75) 式
[B] Advection Phase	\(\widetilde{u} \rightarrow u^{n+1}, \widetilde{h} \rightarrow h^{n+1}\)	(78) 式, (79) 式

Non-Advection Phase¶

(77) 式で \(u^n \rightarrow \widetilde{u}\) を計算して同時に (75) 式で \(h^n \rightarrow \widetilde{h}\) を行うので, (77) 式を以下のように表します.

(80)¶\[{{\widetilde{u}-u^n}\over{\Delta t}} = -g \displaystyle{ \left( {{\partial \widetilde{h}}\over{\partial x}} + {{\partial z_b}\over{\partial x}} \right) }\]

これより,

(81)¶\[\widetilde{u}= u^n - g \Delta t {{\partial \widetilde{h}}\over{\partial x}} - g \Delta t {{\partial z_b}\over{\partial x}}\]

一方, (75) 式で \(h^n \rightarrow \widetilde{h}\) を求めるので,

(82)¶\[{{\widetilde{h}-h^n}\over{\Delta t}} + {{\partial}\over{\partial x}} (\widetilde{u} \widetilde{h} ) =0\]

を満たす必要があります. したがって, (81) 式と (82) 式を連立して得られる \(\widetilde{h}\) および \(\widetilde{u}\) を求める必要があります.

CIP法で流体の計算を行う場合は一般に \(u\) と \(h\) の計算点を交互に配置するスタッカード格子が用いられます. ここでは, Figure 24 に示すような計算点の配置を採用することにします.

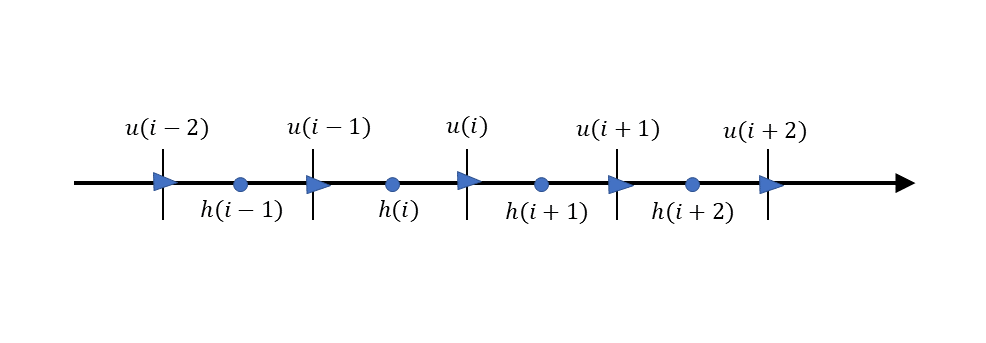
_images/1d_stk.png — Figure 24 : スタッカード格子¶

この計算点の配置を考慮して (81) 式を差分表示すると,

(83)¶\[\widetilde{u}(i) = u^n(i)-g\Delta t {{\widetilde{h}(i+1) - \widetilde{h}(i)}\over{\Delta x}} -g\Delta t {{z_b(i+1) - z_b(i)}\over{\Delta x}}\]

となり( \(z_b\) の計算点は \(h\) の計算点と同じとする), これを (82) 式の左辺第2項に代入するために,

(84)¶\[\widetilde{q}=\widetilde{u} \widetilde{h}\]

なる単位幅流量 \(q\) を導入し( \(q\) の計算点は \(u\) と同じとする), 格子点の配置を考慮して,

(85)¶\[\widetilde{q}(i)= \widetilde{u}(i) {{\widetilde{h}(i+1)+\widetilde{h}(i)}\over{2}}\]

および, \(q\) を用いた (82) 式の差分式

(86)¶\[\widetilde{h}(i) = h^n(i) - \left[ \widetilde{q}(i)-\widetilde{q}(i-1) \right] {{\Delta t}\over{\Delta x}}\]

より \(\widetilde{h}\) を求めることが出来ます. ただし, (86) 式には右辺の \(\widetilde{q}\) にも \(\widetilde{h}\) が陰な形式で含まれるため, Figure 25 に示すような繰り返し計算が必要になります.

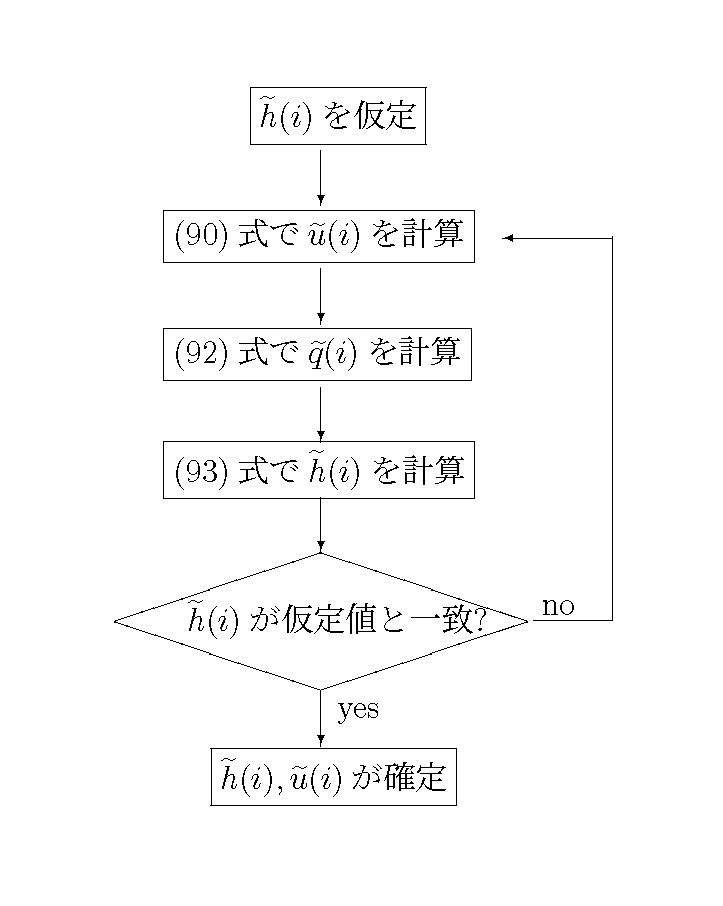
_images/flow_chart.png — Figure 25 : Non-Advection Phase における \(\widetilde{h}(i)\) および \(\widetilde{u}(i)\) の計算手順¶

この繰り返し計算を通して得られる \(\widetilde{h}(i)\) および \(\widetilde{u}(i)\) がNon-Advection Phaseの計算結果です.

Non-Advection Phaseにおける \(\widetilde{u}(i)\) が求まった段階で, Non-Advection Phaseにおける \(\displaystyle{\widetilde{{\partial u}\over{\partial x}}}\) を求めておく必要があります. これは, 前記の (61) 式で \(f\) を \(u\) と置いた次式で求めることが出来ます.

(87)¶\[\widetilde{{\partial u}\over{\partial x}}(i)= {{\partial u}\over{\partial x}}^n(i)+{{1}\over{2\Delta x}} \left[ \widetilde{u}(i+1)-u^n(i+1)-\widetilde{u}(i-1)+u^n(i-1) \right]\]

Advection Phase¶

Advextion Phaseにおいては (78) 式に直接CIP法を適用することが出来ます. 即ち, (62) 式で \(f\) を \(u\) と置いて次式で求めることが出来ます.

(88)¶\[{u(i)}^{n+1}=U(X)= \left[(aX+b)X+ \widetilde{{\partial u}\over{\partial x}}(i) \right] X +\widetilde{u}(i)\]

ただし, \(\widetilde{u}(i)\) および, \(\displaystyle{\widetilde{{\partial u}\over{\partial x}}(i)}\) はそれぞれNon-Advection Phaseにおける \(u\) および \(u\) の空間微分量であり, それぞれ, (83) 式および (87) 式で求まった値です. また, \(a\) および \(b\) は前章の (50) 式で \(f\) を \(u\) としたものを使用します．

従って, Advection Phaseにおける \(u\) は \(U(X)\) を用いて,

(89)¶\[u(i)^{n+1}= U(X)\]

となります. Advection Phaseにおける \(u\) の空間微分量は同様には, 前章の (68) 式および (70) 式で \(f\) を \(u\) としたものを用いて,

(90)¶\[\widehat{{\partial u}\over{\partial x}}(i) = 3aX^2 + 2bX + \widetilde{{\partial u}\over{\partial x}}(i)\]

および

(91)¶\[{{\partial u}\over{\partial x}}^{n+1}(i) = \widehat{{\partial u}\over{\partial x}}(i) -{{u(i+1)-u(i-1))}\over{2\Delta x}}\widehat{{\partial u}\over{\partial x}}(i) \Delta t\]

で求めることができます.

境界条件¶

本計算法では \(u\), \(h\) の境界条件の他に CIP法を用いるために \(\displaystyle{{\partial u}\over{\partial x}}\) の境界条件も必要になります. 計算の対象としている現象に即した物理的な境界条件が必要となりますが, 最も単純な条件としては全ての変数に対して,

(92)¶\[{{\partial}\over{\partial x}} =0\]

という方法がありこれは自由境界条件ということになります. なお，水位(水深)については，計算条件に応じて適宜選択する必要があります．詳細は省略しますが，常流においては下流端の水位(水深)境界条件を，射流においては上流端の水位(水深)境界条件を与えることが出来ます．なお, 当然のことですが境界条件は Non-Advection PhaseとAdvection Phaseの両方に適用する必要があります.

まとめ¶

以上の1次元自由水面を有する流れの計算をまとめると以下のフローチャートとなります.

_images/flow_chart2.png — Figure 26 : 1次元自由水面を有する流れの計算フローチャート¶

Pythonコード¶

上記1次元非定常流れの計算コードの例を下記に示します．

https://github.com/YasuShimizu/1D-Free-Water-Surface

このGitHubのフォルダにある拡張子がpyのファイルが計算用のファイル群ですが，このうちmain.pyが計算コードの本体で，この中の下記部分で，ymlファイル名をコメントアウトしてある部分を逐次有効にすることにより異なる条件の水面計計算が可能となります．

with open('config.yml','r', encoding='utf-8') as yml:
#with open('config_jump.yml','r', encoding='utf-8') as yml:   #跳水
#with open('config_trans.yml','r', encoding='utf-8') as yml:  #遷移流
#with open('config_back_water.yml','r', encoding='utf-8') as yml:   #堰上げ背水
#with open('config_drop_down.yml','r', encoding='utf-8') as yml:   #低下背水
#with open('config_bump.yml','r', encoding='utf-8') as yml:   #突起のある流れ
    config = yaml.load(yml)

ymlファイルは計算条件を記述したファイルで，上記GitHubサイトに含まれてます．一例として[config_trans.yml]を下記に示します．コメントにある項目を適宜修正することにより条件を変更しながら計算を行うことが出来ます．なお，計算法の説明では簡単のために摩擦を無視した場合で説明しましたが，計算コードでは運動方程式に摩擦項を追加してあります．ymlファイルで粗度係数をゼロとすれば摩擦を無視した流れの計算が出来ます.

xl : 200 # 水路長(m)
nx: 51  # x方向格子数
j_channel: 2 # 水路の状態 1=一定勾配 2=勾配変化点あり
# j_channel=1の場合
slope: 0.002 # 全体の勾配
# j_channel=2の場合
x_slope : 130 # 勾配変化点
slope1 : 0.001 # 上流側勾配
slope2 : 0.01 # 下流側勾配
xb1 : 4 # 突起始り位置の上流端からの距離(m)
xb2 : 5 # 突起頂点の上流店からの距離(m)
xb3 : 6 # 突起終了点の上流店からの距離(m)
dbed : 0.00 #突起高さ(m)
qp : 1 #単位幅流量(m**2/2)
g : 9.8 #重力加速度
snm : 0.025 # 粗度係数
alh : 0.6 # 水位計算緩和係数
lmax : 50 # 水位計算最大繰り返し回数
errmax : 0.0001 # 打ち切り誤差
hmin : 0.01 # 最小水深(m)
j_upstm : 2 # 上流端の条件 1=Wall, 2=Free, 3=Fixed Value
j_dwstm : 3 # 下流端の条件
alpha_up: 1.0 # 上流端の水深(等流水深に対する割合)
alpha_dw: 1.0 # 下流端の水深(等流水深に対する割合)

etime : 400 # 計算終了時間(sec)
dt : 0.05 # 計算タイムステップ(sec)
tuk : 10 # アウトプットインターバル(sec)

なお，[config_trans.yml]中の xb1, xb2, xb3 および dbed は下図のような定義とします．

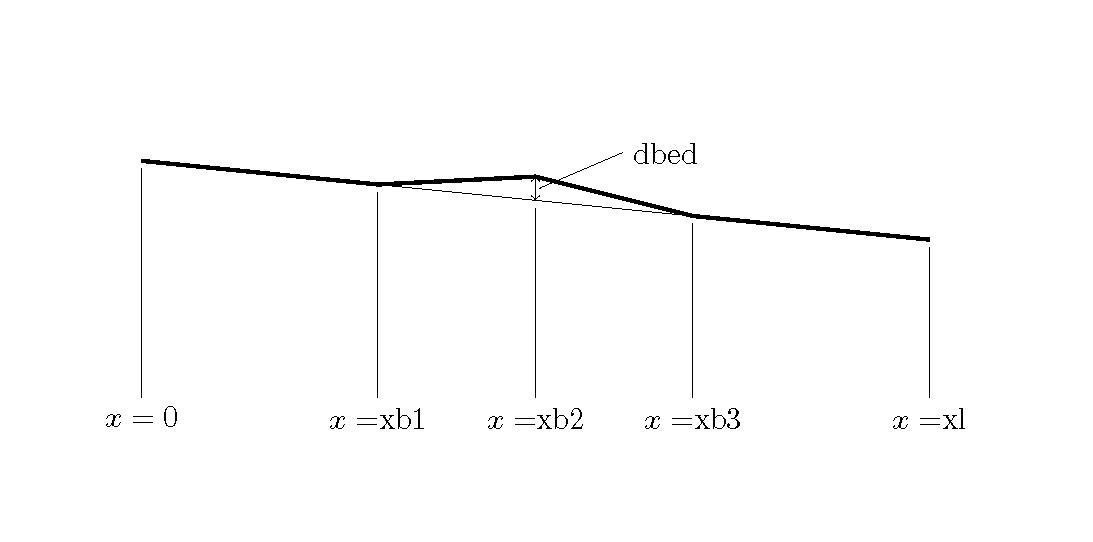
_images/bed_cond.png — Figure 27 : 河床突起の設定パラメーター¶

計算例¶

堰上げ背水¶

[config_back_water.yml]を使用した計算例を下記に示します．計算結果は，上から水位(Water)，河床形状(Bed)，流速(Velocity)，単位幅流量(Discharge，フルード数(Fr)の縦断形です．水位縦断には以下の (93) 式による等流水深 \(h_0\) および限界水深 \(h_c\) も併記してあります．

(93)¶\[h_0=\left(\cfrac{q n}{\sqrt{i}}\right)^{3/5}, \ \ h_c=\left(\cfrac{q^2}{g}\right)^{1/3}\]

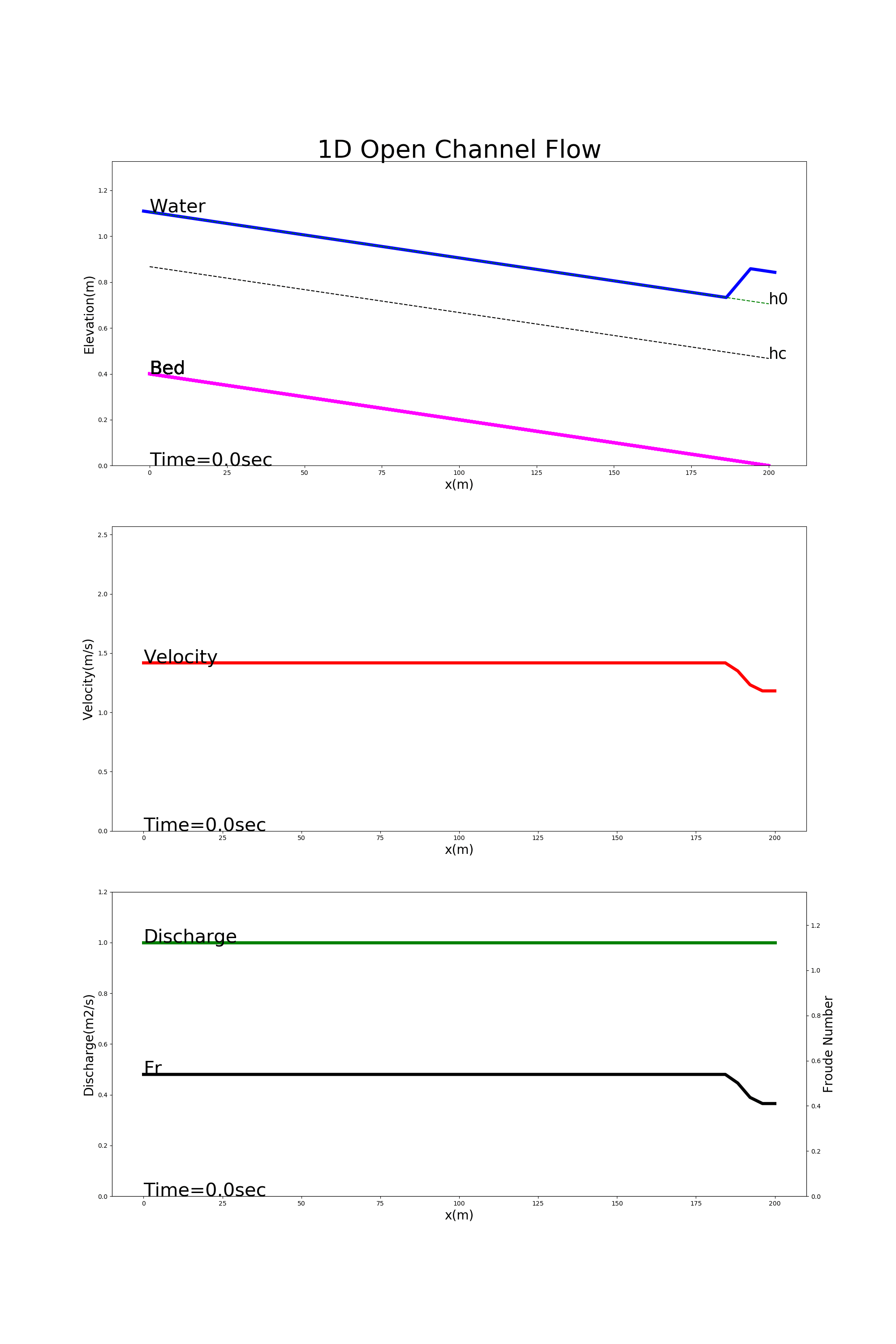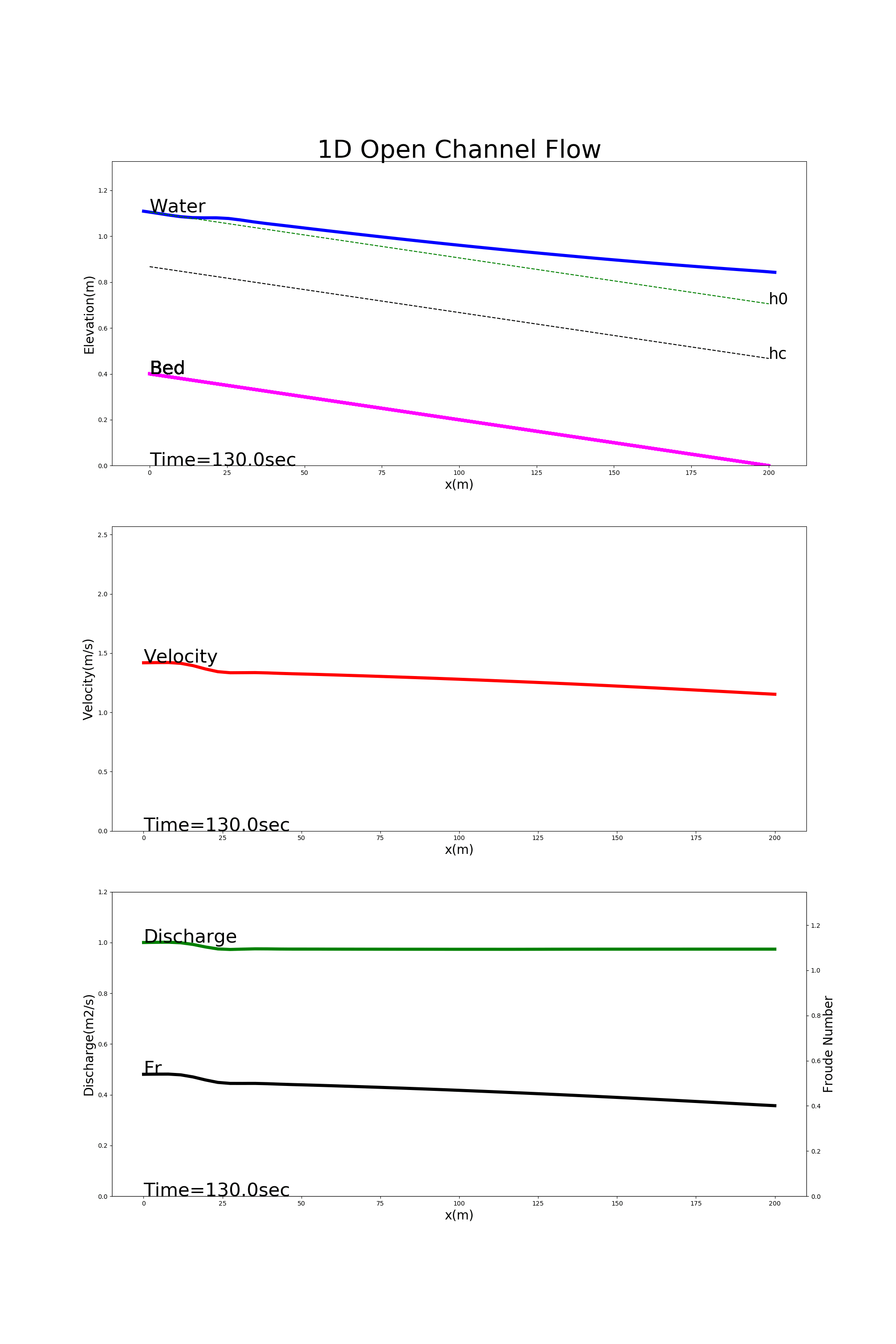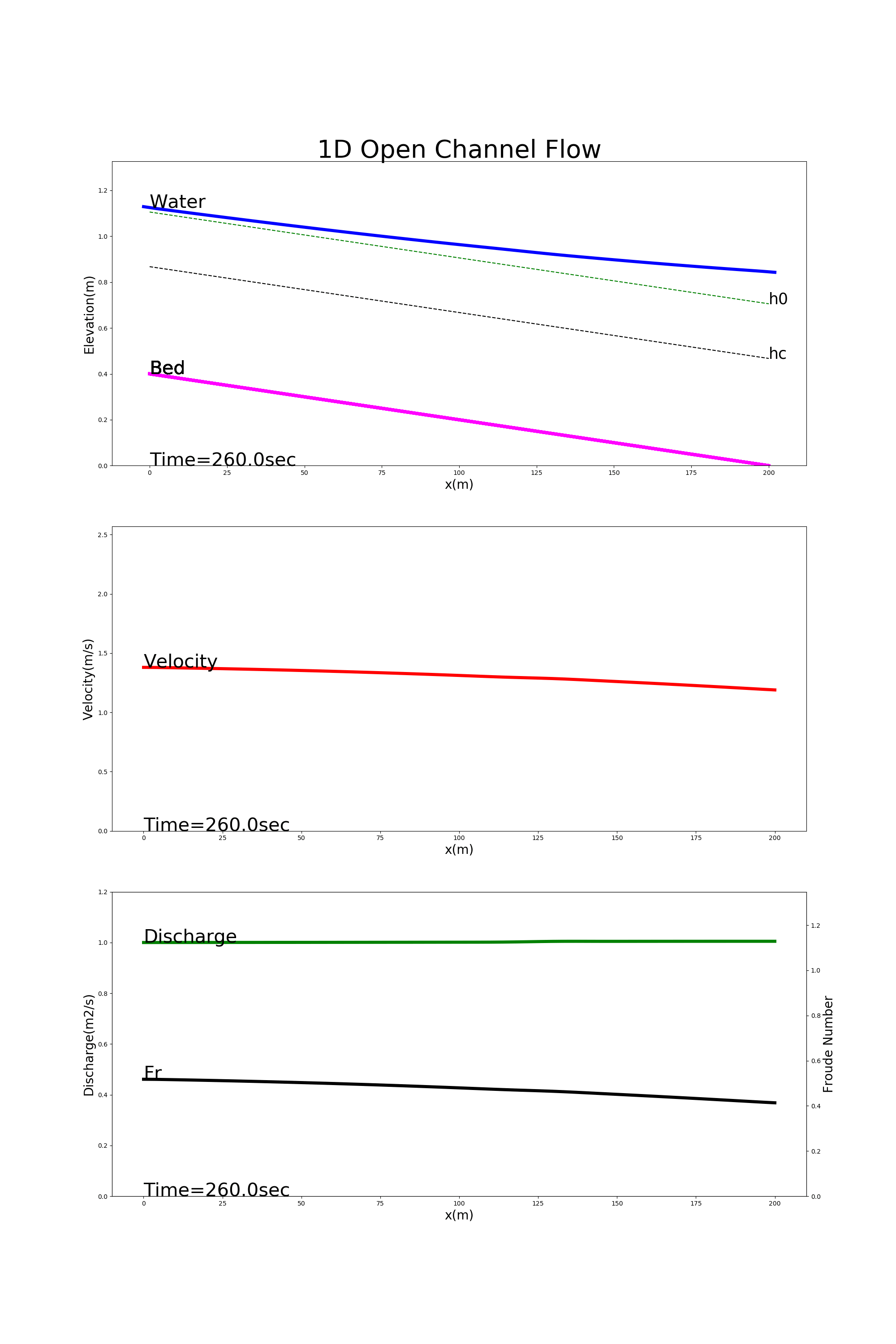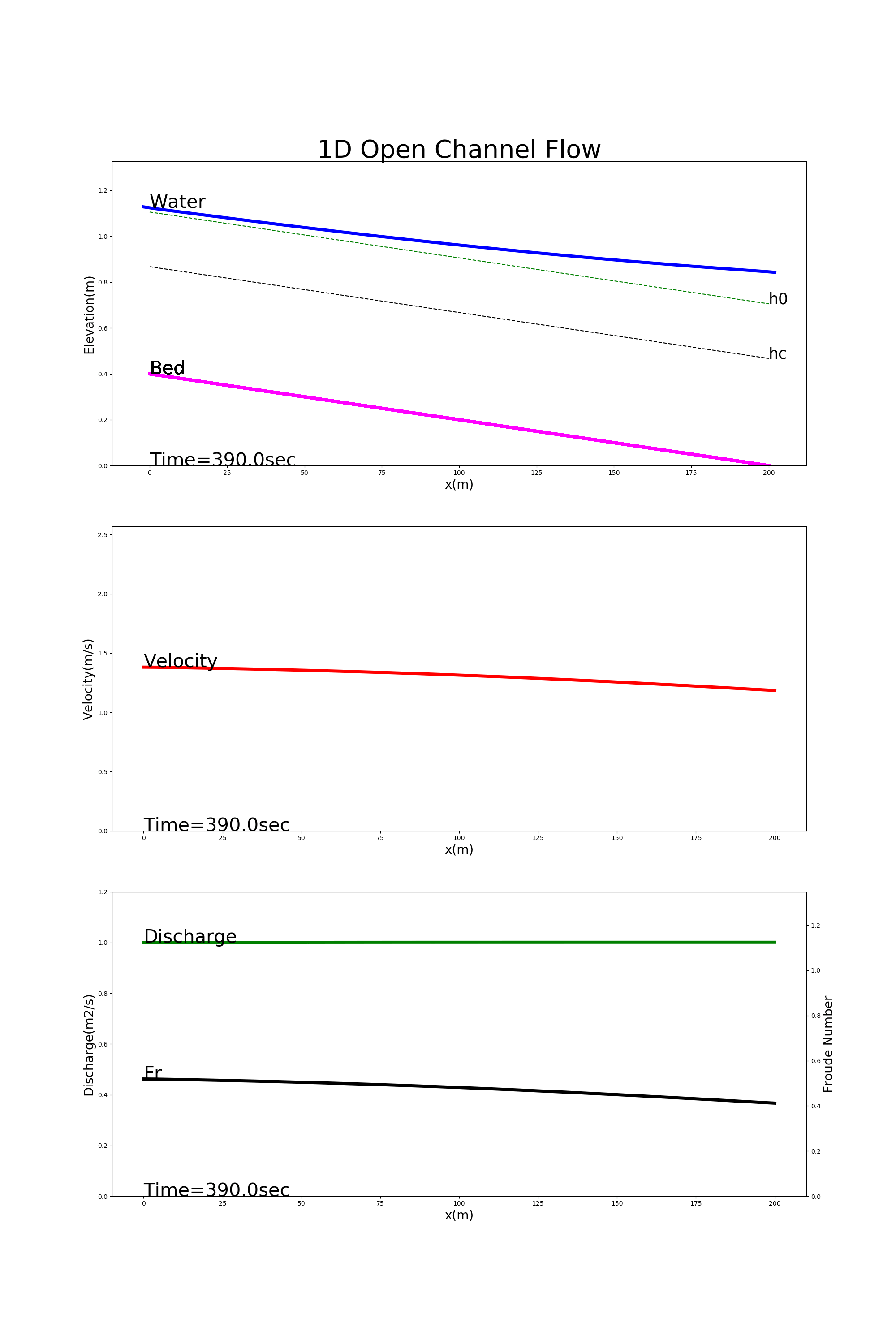
_images/back_water.gif — Figure 28 : 堰上げ背水の計算例¶

Figure 28 の計算では，下流端で等水深より20%深い水深に堰上げられた水位の影響が上流へ伝わる様子が計算されています．

低下背水¶

[config_drop_down.yml]を用いた計算結果を Figure 29 に示します．この例では，下流端で等流水深の70%に保たれた下流端水深を境界条件とる低下背水の様子が計算されています．

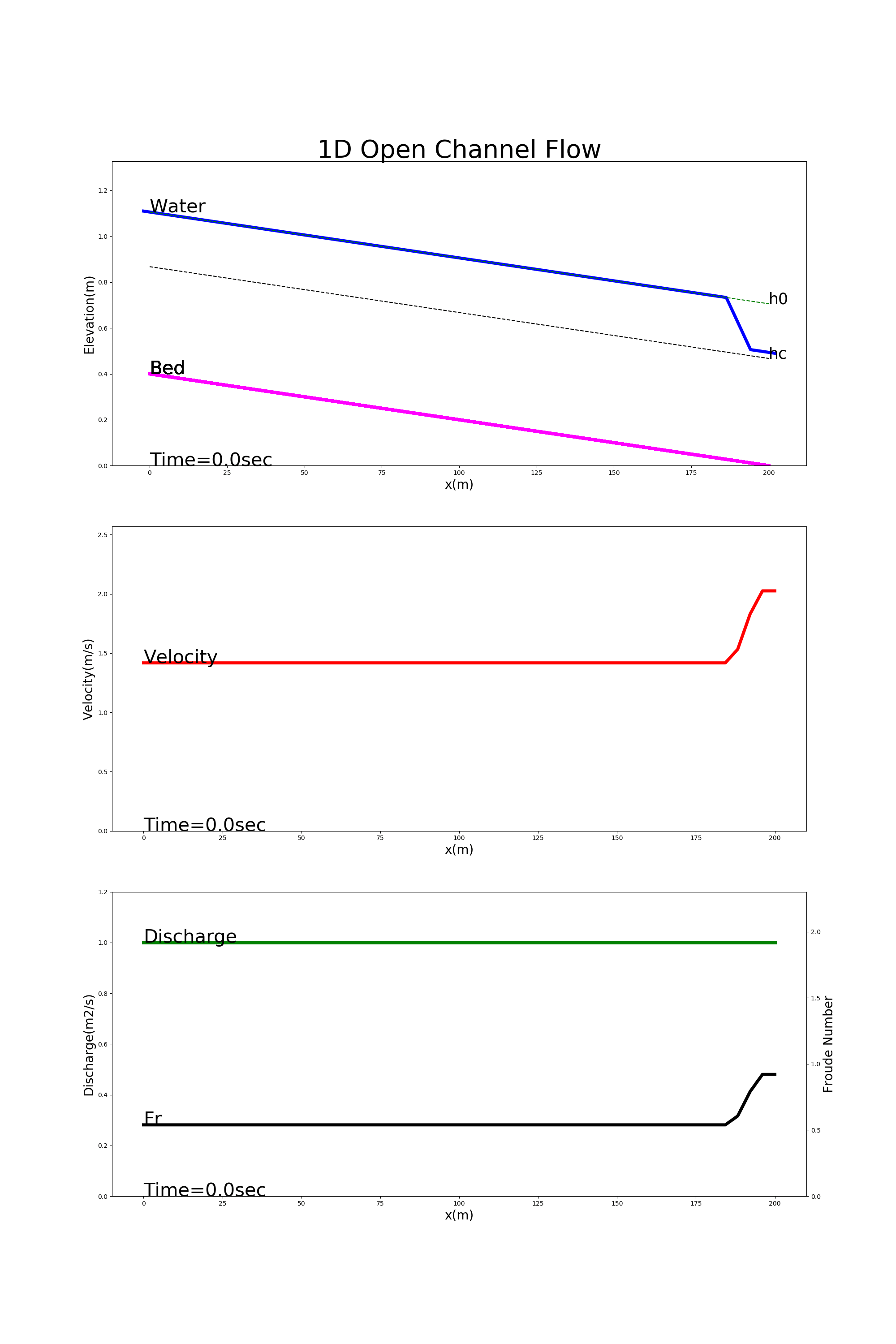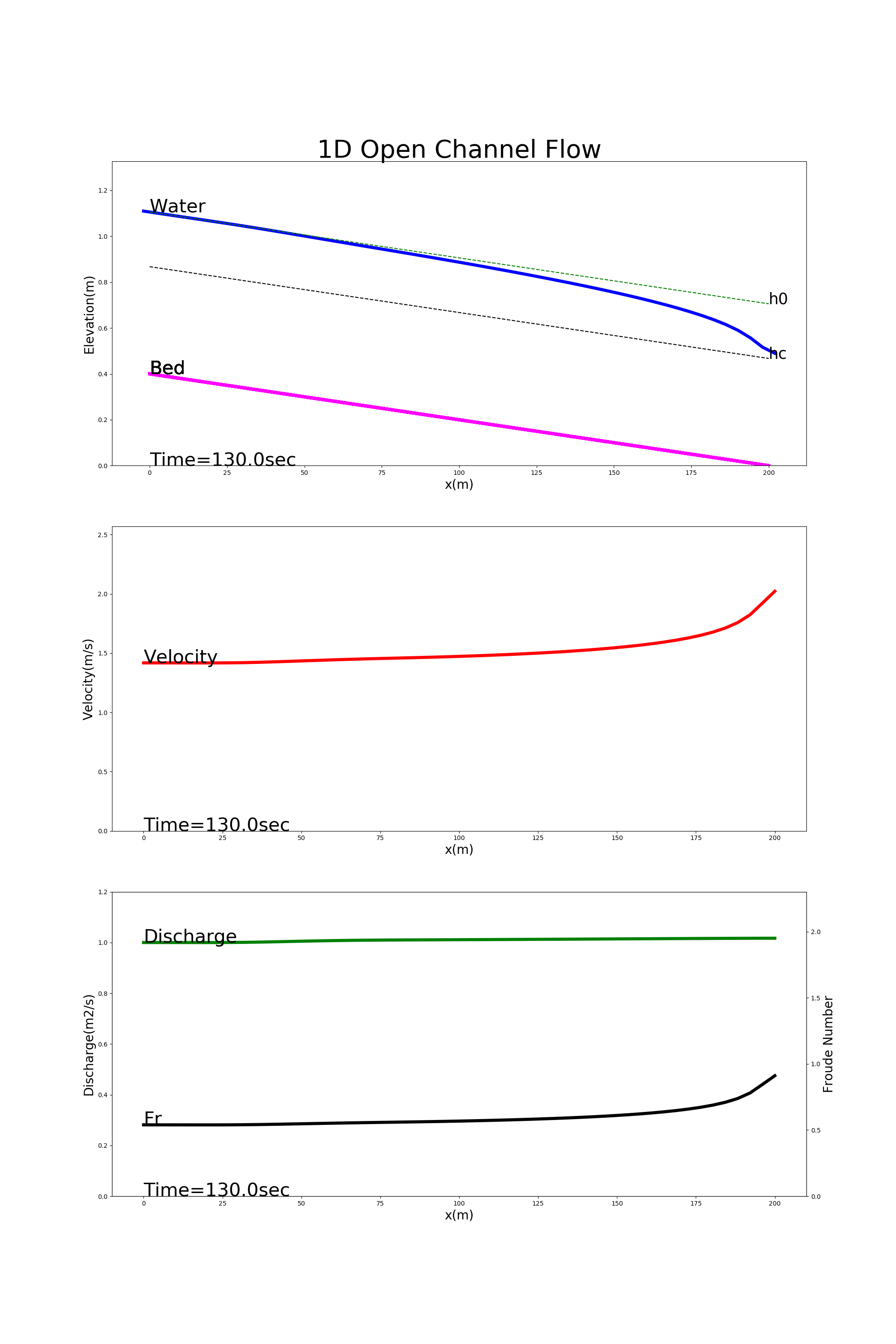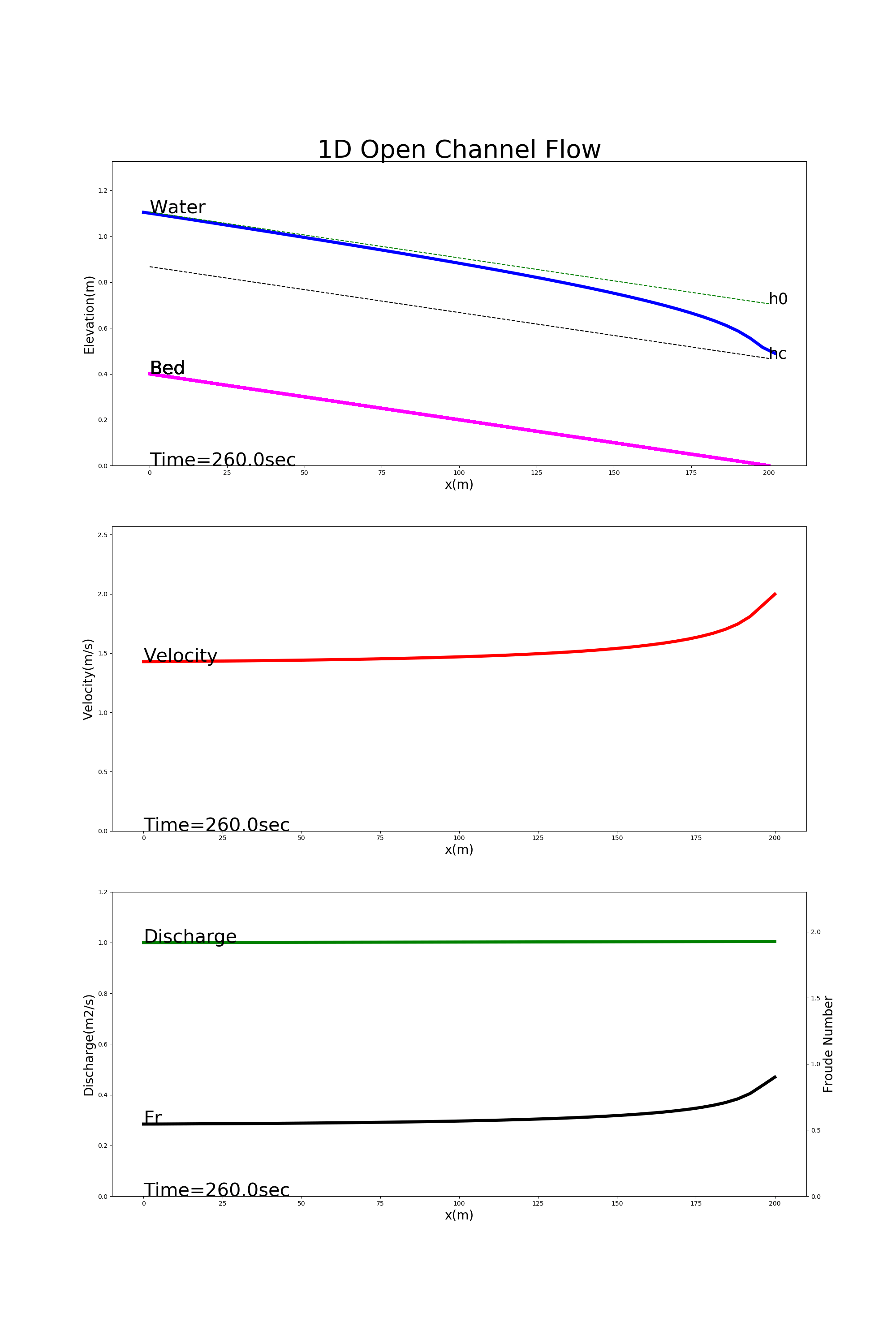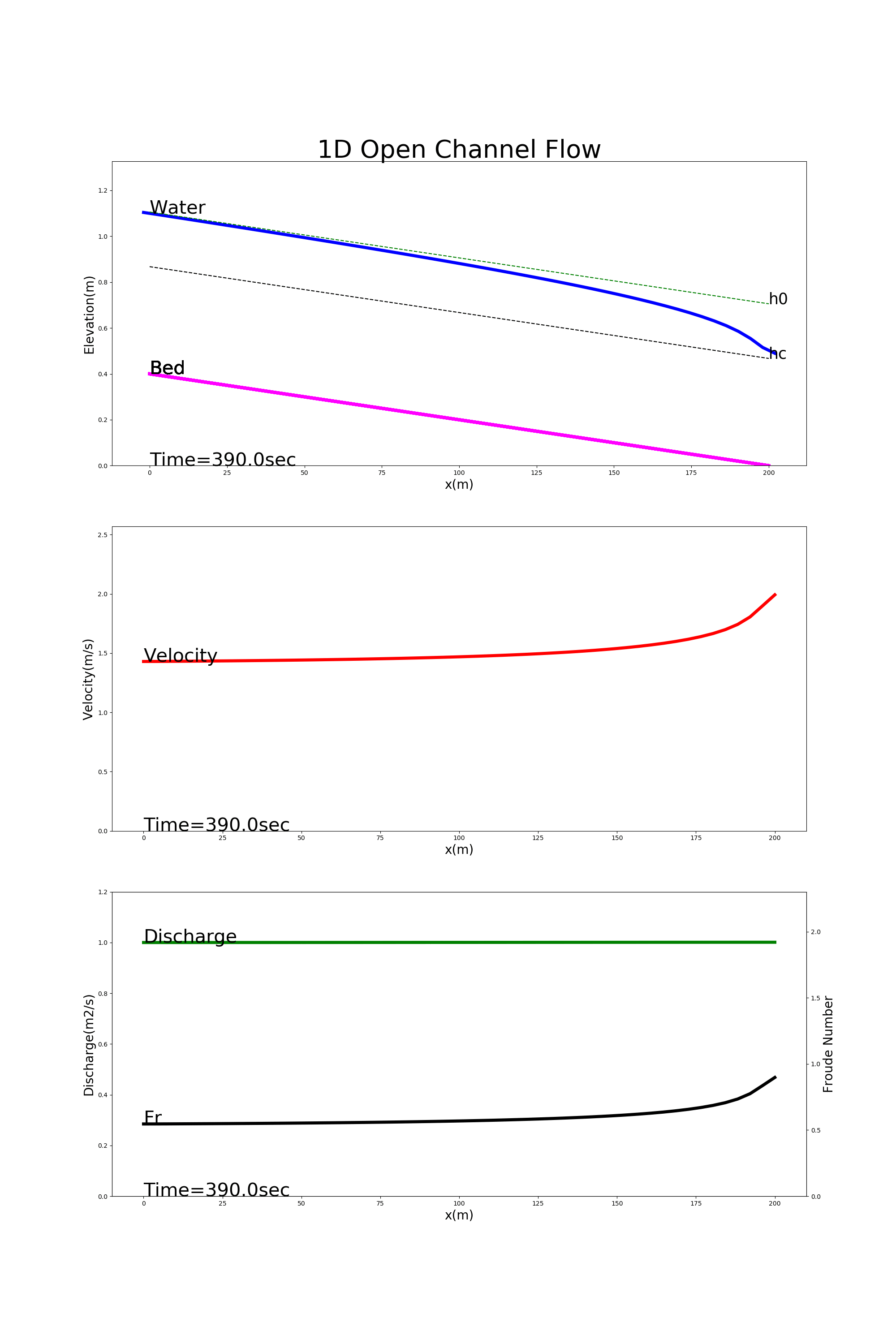
_images/drop_down.gif — Figure 29 : 低下背水の計算例¶

跳水¶

[config_jump.yml]を用いた計算結果を Figure 30 に示します．この例では，上流側が急こう配，下流側が緩勾配になっている水路における跳水の様子が計算されています．

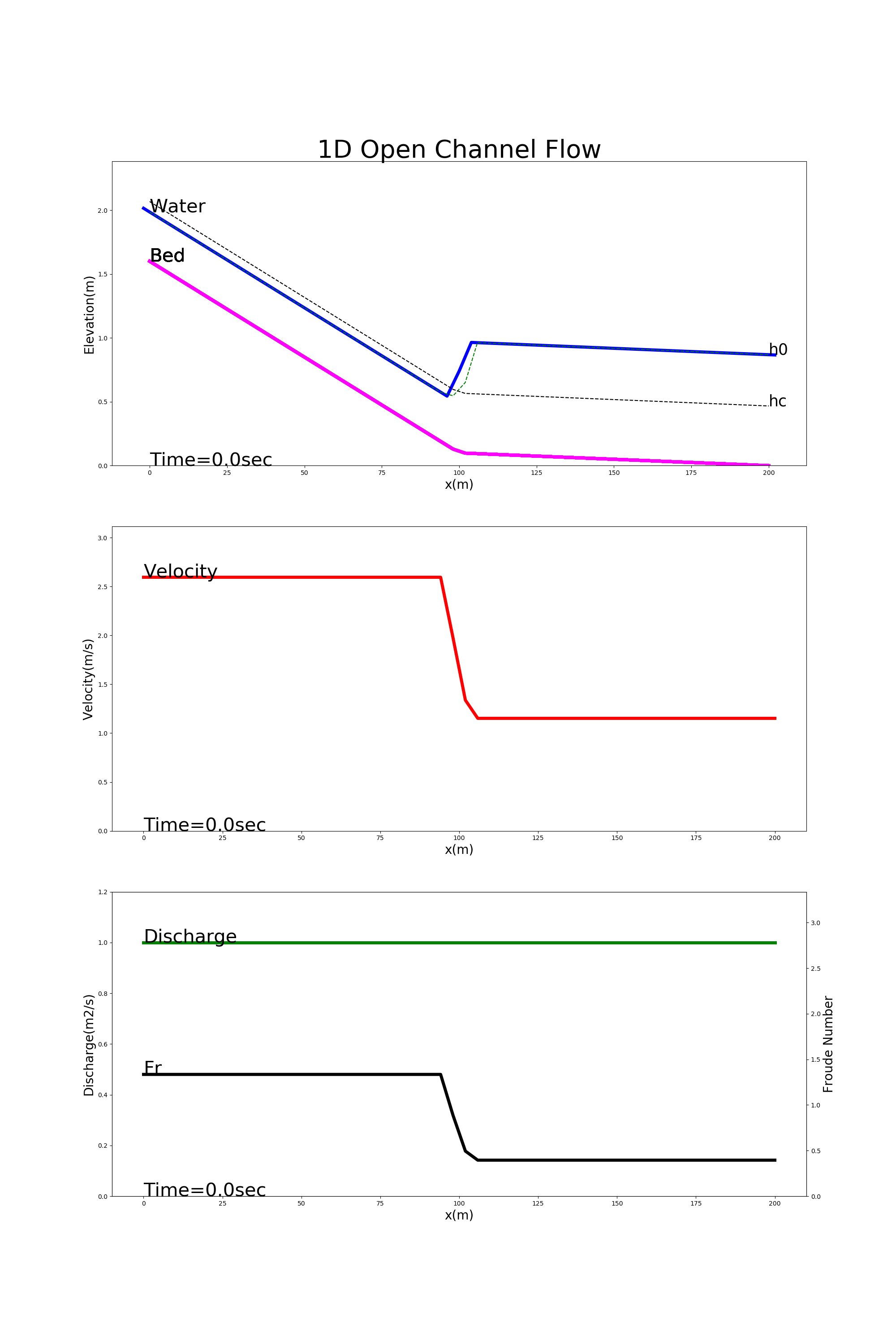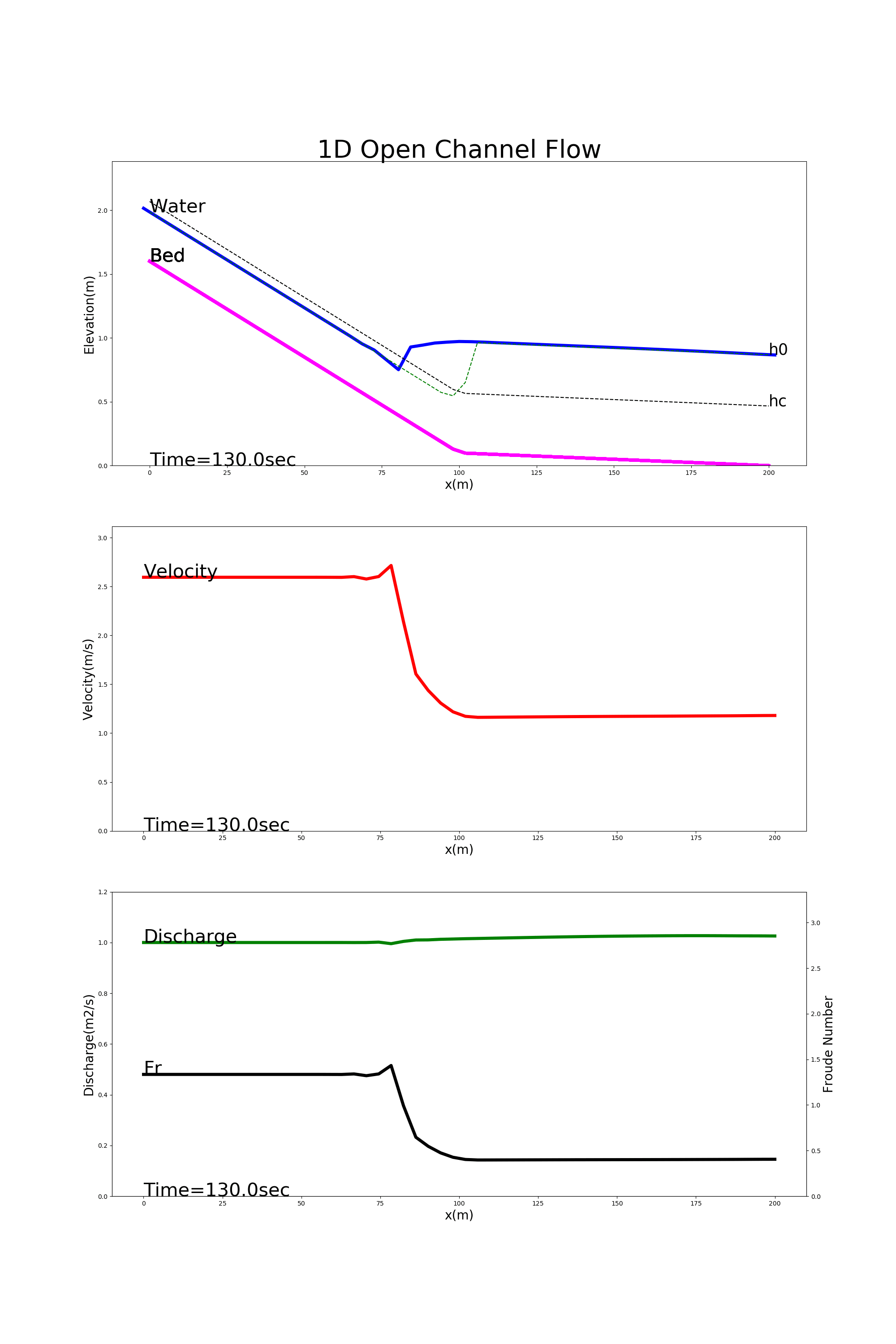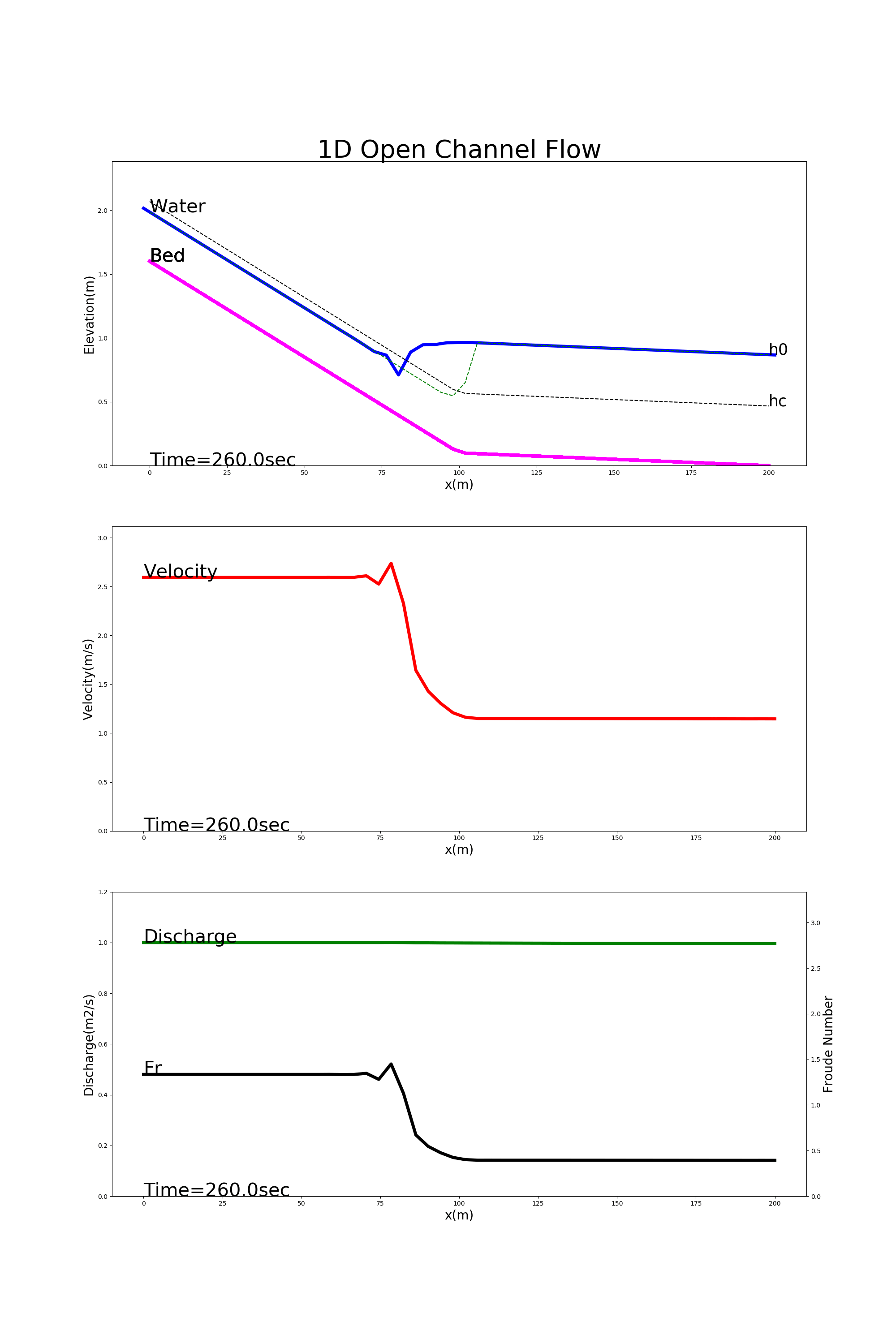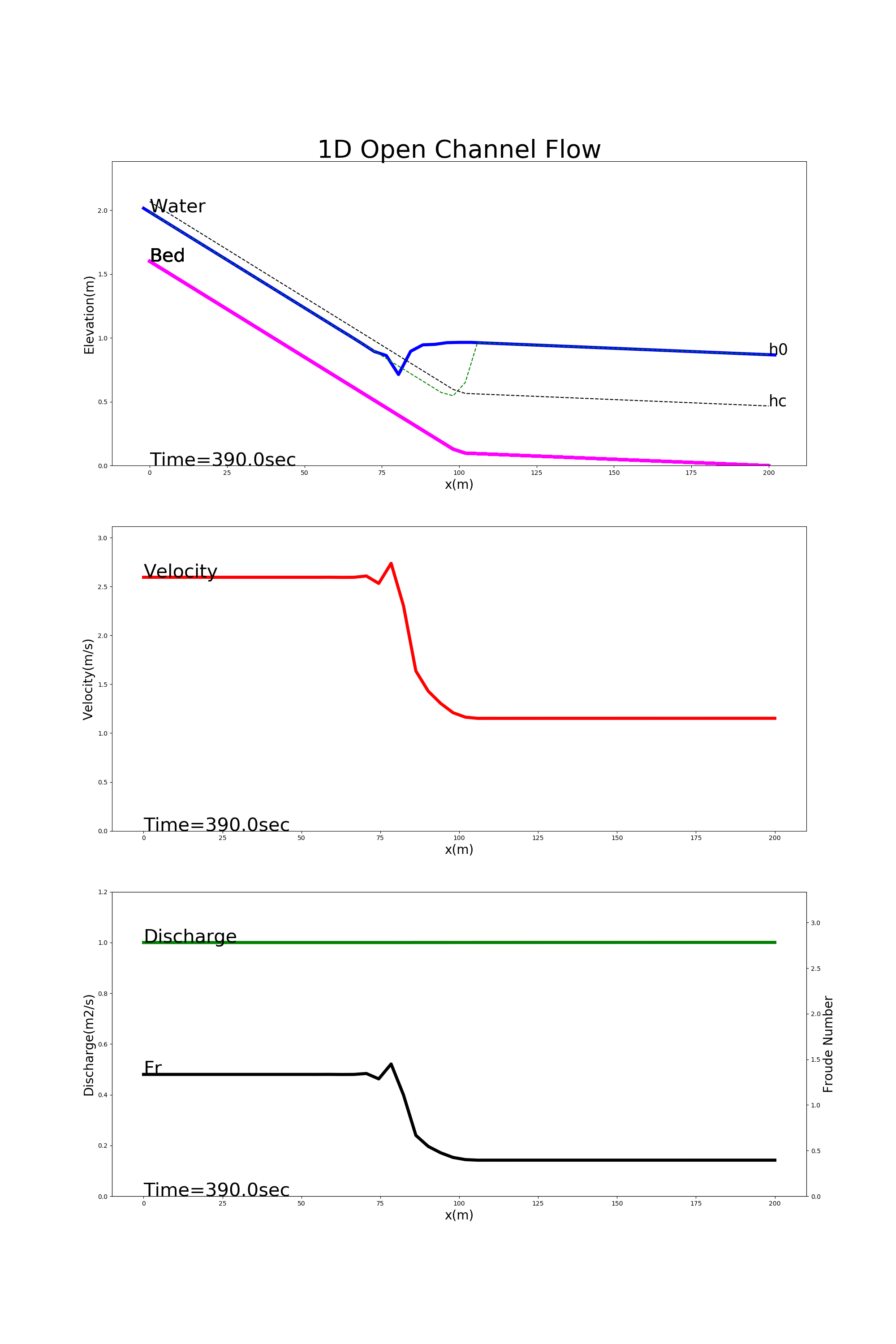
_images/jump.gif — Figure 30 : 低下背水の計算例¶

遷移流¶

[config_trans.yml]を用いた計算結果を Figure 31 に示します．この例では，上流側が緩勾配，下流側が急こう配になっている水路で常流から射流に遷移する流れの様子が計算されています．

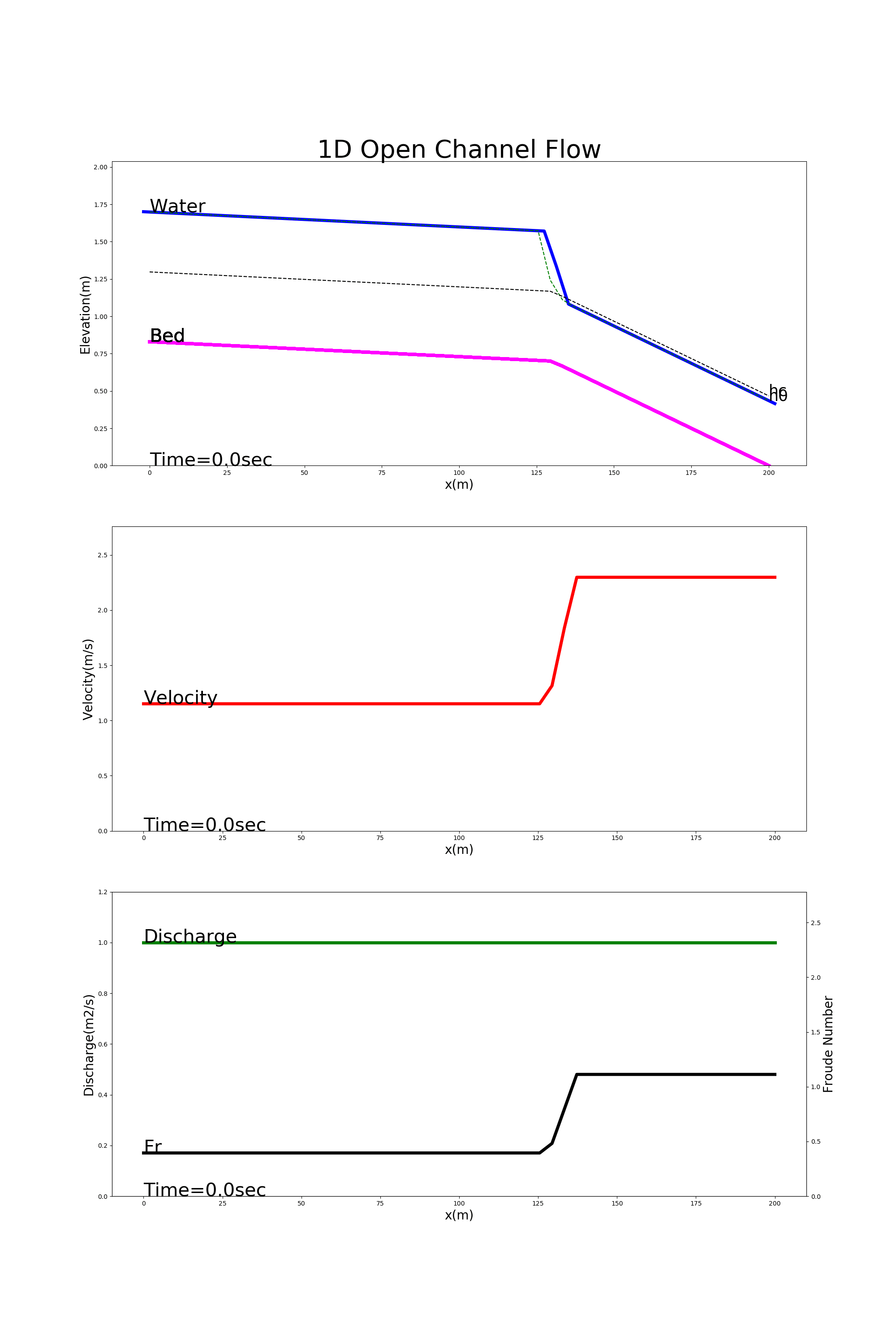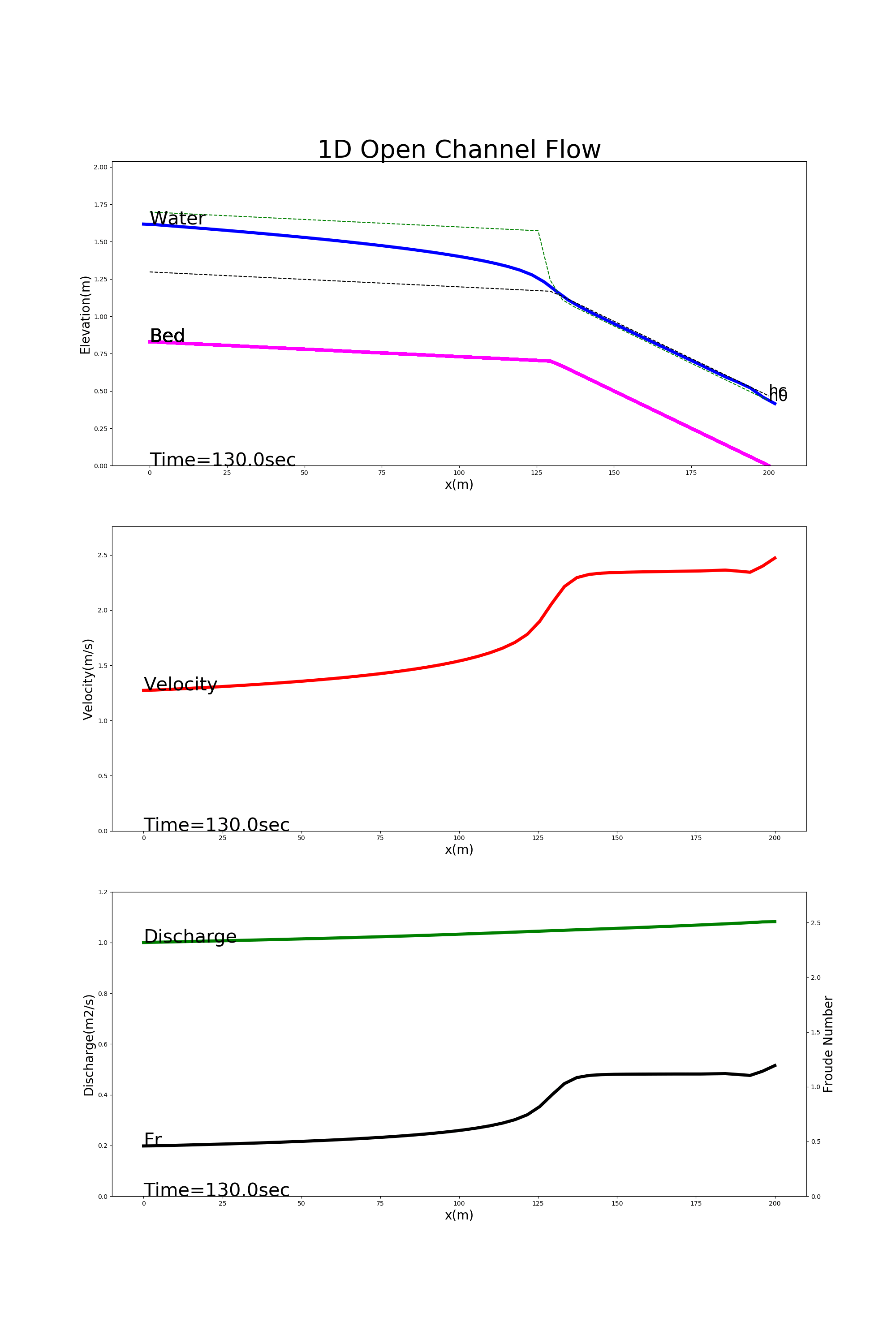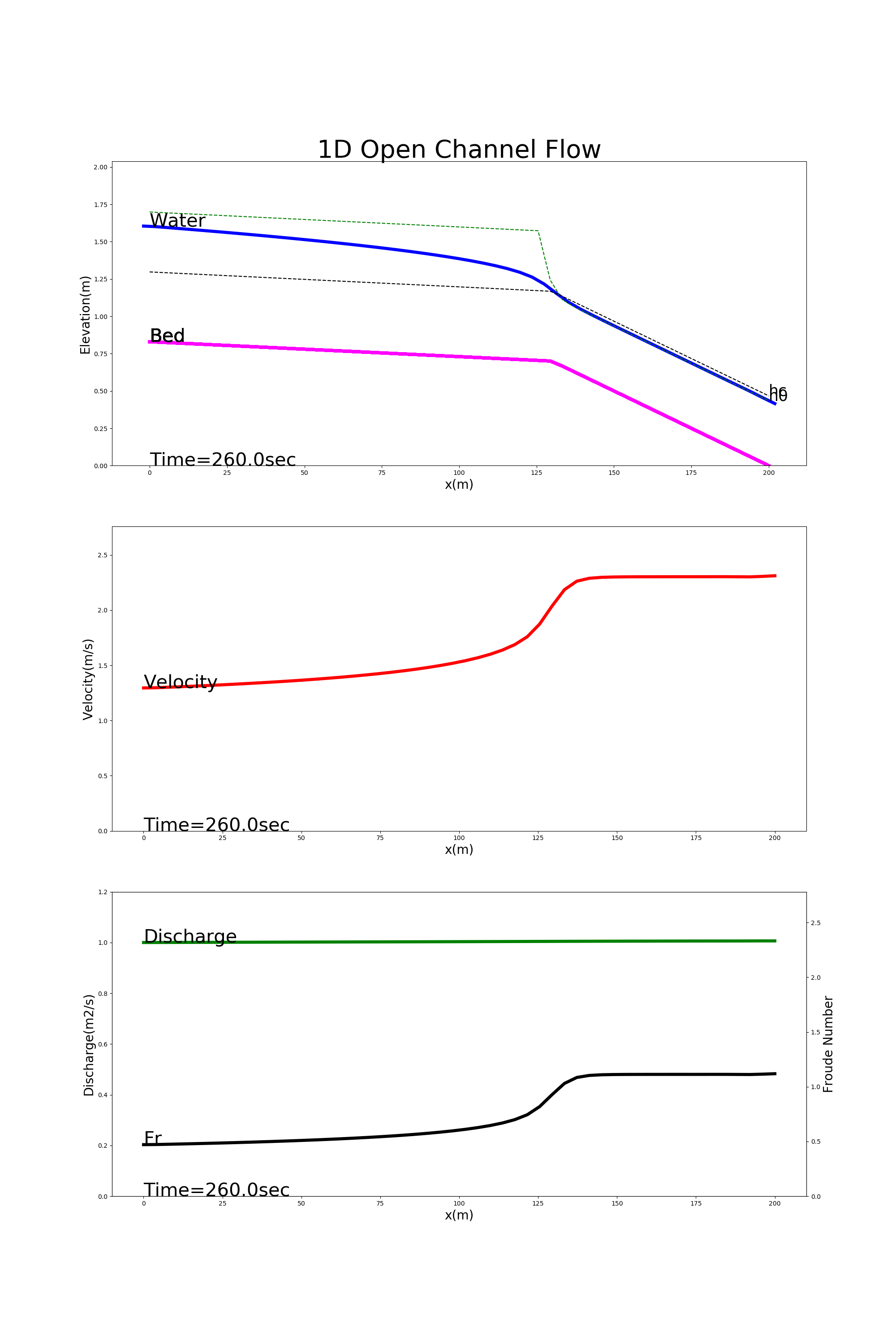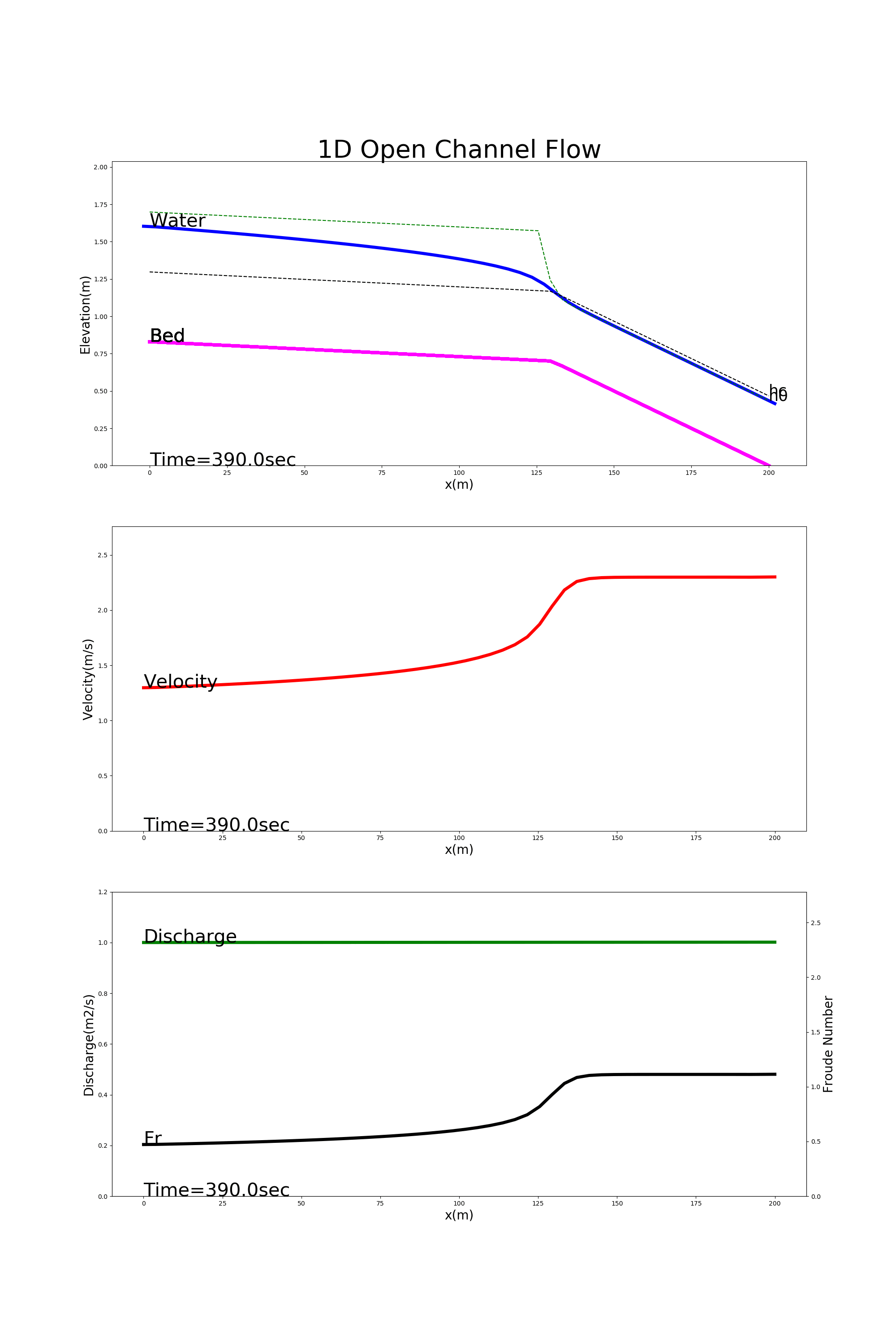
_images/trans.gif — Figure 31 : 遷移流の計算例¶

水路中央に突起がある流れ¶

[config_bump.yml]を用いた計算結果を Figure 32 に示します．この例では，水路中央部に突起がある流れの様子が計算されています．この例は常流なので，突起部分で水位は低下している様子が計算されています．（水理学で習いましたよね？覚えていますか？）

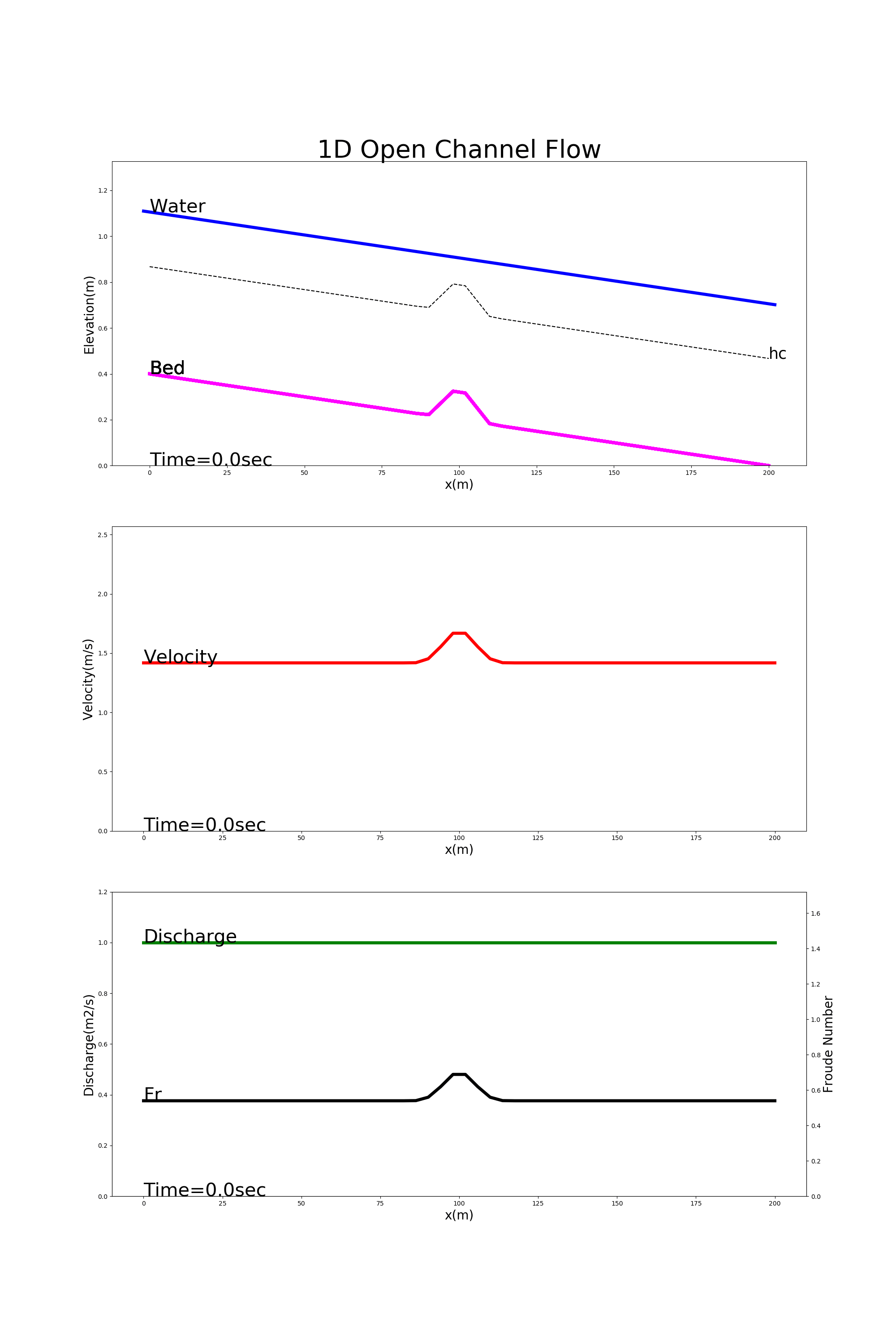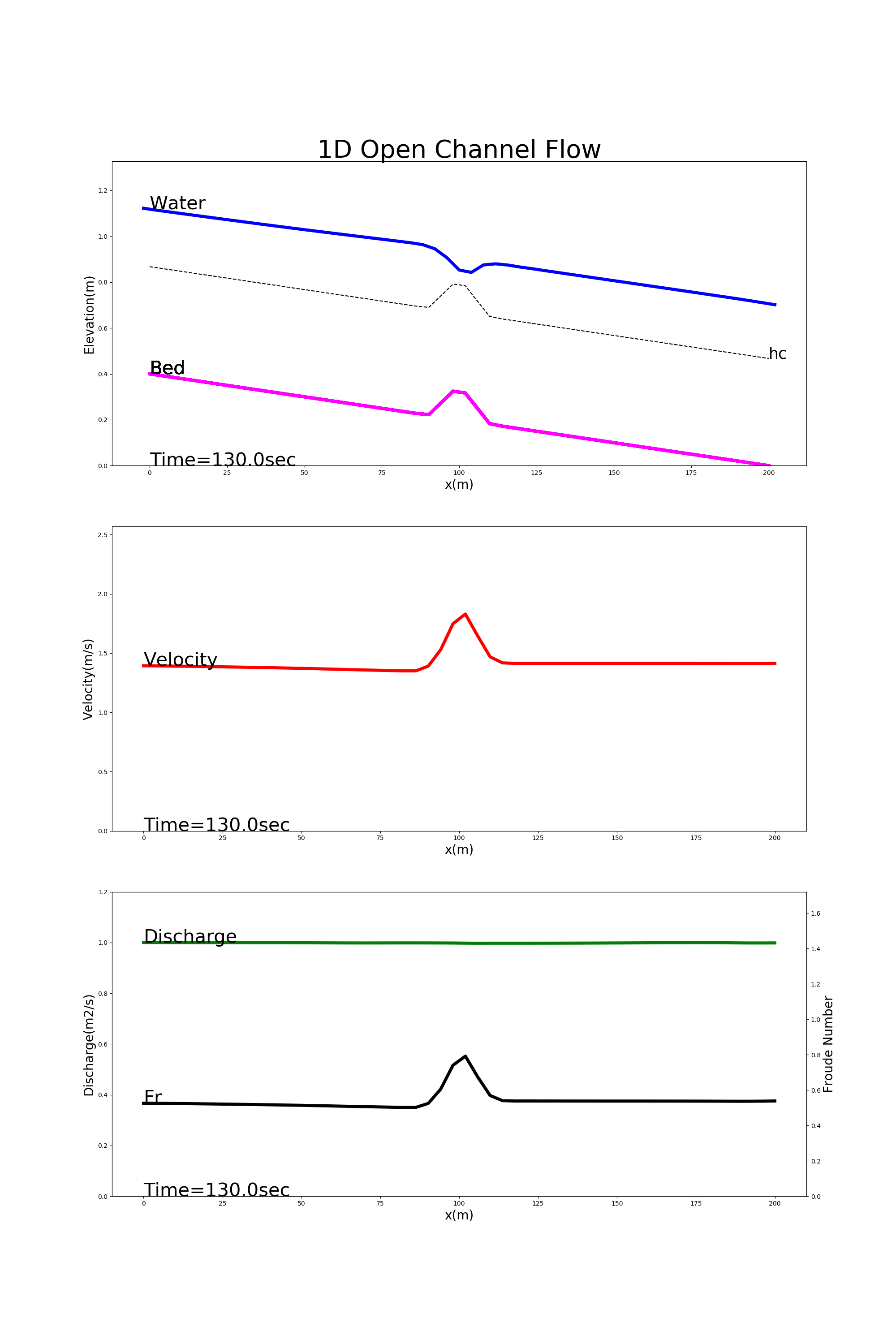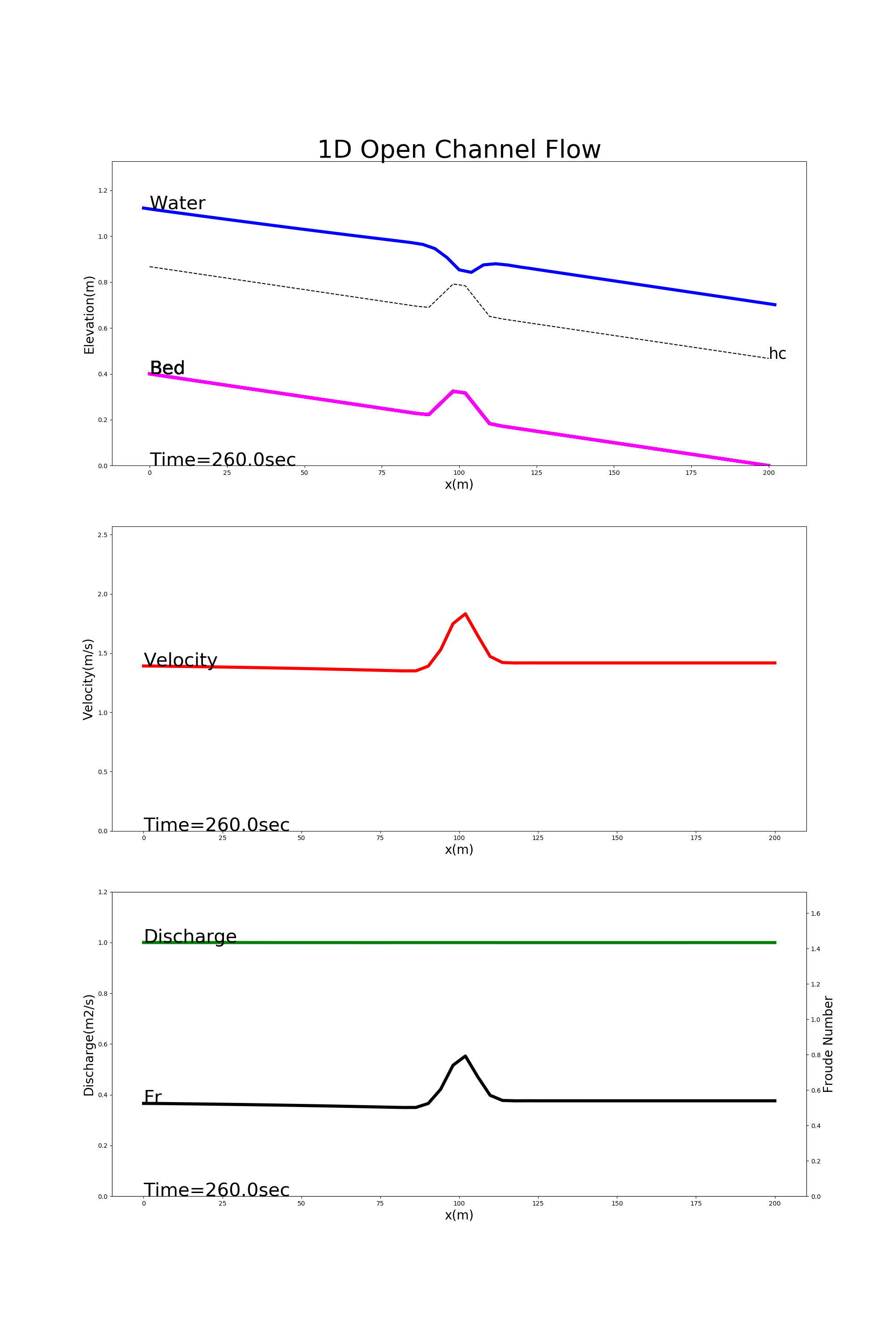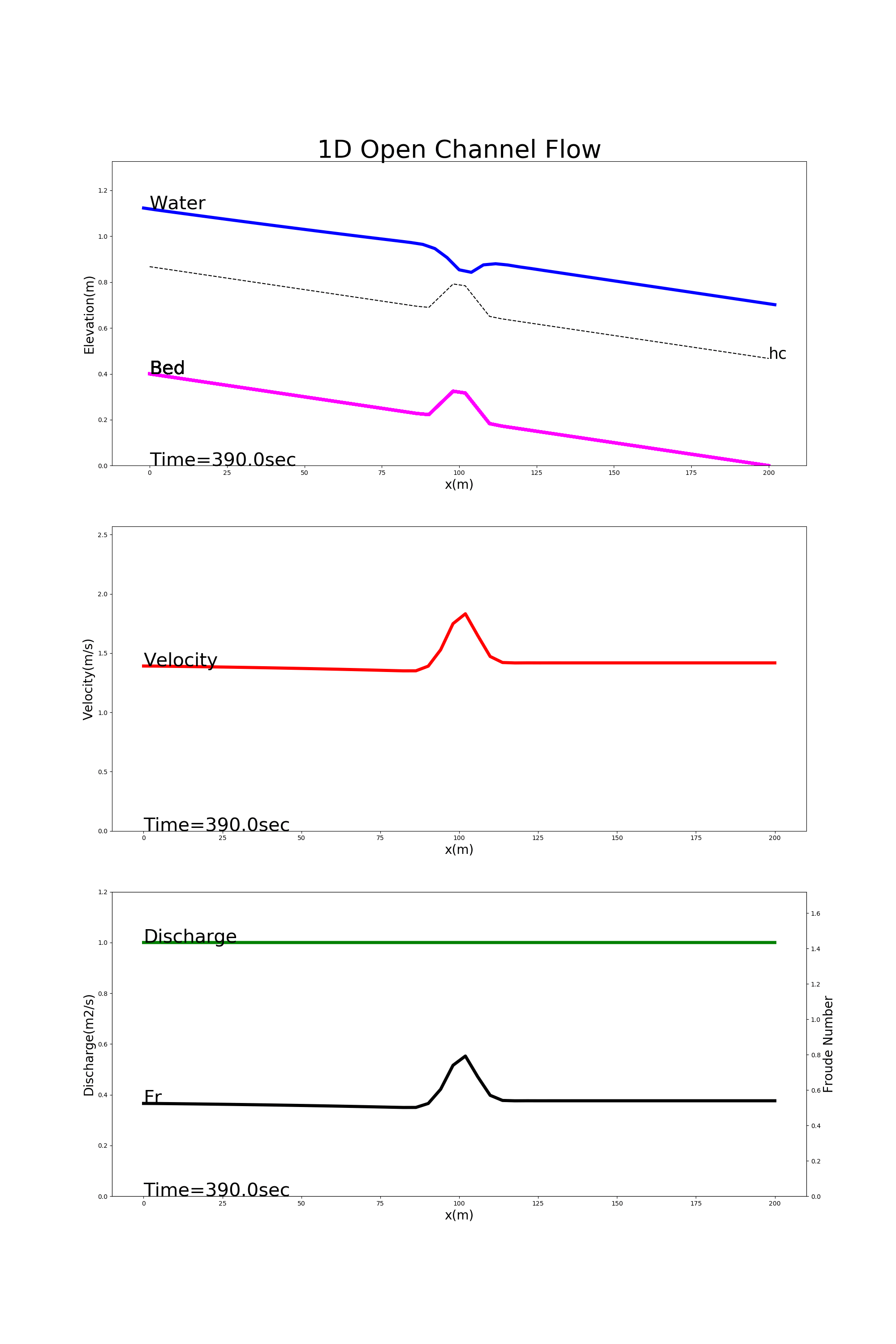
_images/bump.gif — Figure 32 : 水路中央に突起がある流れ（常流）の計算例¶