この節の作者: 清水康行 <yasu@i-ric.org>

本テキストへの感想, 質問, 要望, バグ報告などはこちらへお願いします.

高精度風上差分法

変数の格子間分布の補完

いま， Figure 14 に示すように黒線で示す三角形分布の変数 \(f\) の時刻 \(t\) における分布 \(f(t)\) が，速度 \(u(>0)\) で \(x\) 方向に移流する状態を想定します．なお，時刻 \(t\) においては 三角形の頂点である \(A\) 点は \(i\) 番目の格子点に位置しているとします． \(\Delta t\) 時間で移動する距離は \(u \Delta t\) なので，図の赤の破線の分布に移動するはずで， ピークは赤丸の \(A'\) 点に移動することになります．

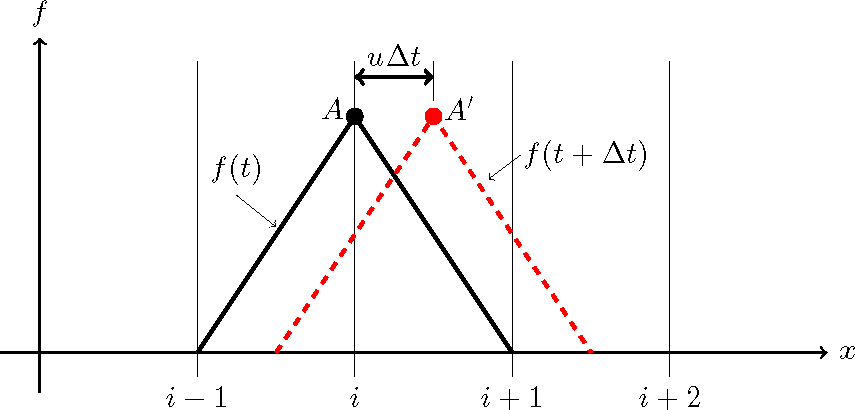
Figure 14 ::変数の移流(1)

ところが，Figure 14 のように実際は \(A'\) 点は計算格子上には無く, \(i\) 番目の格子と \(i+1\) 番目の 格子の間に来てしまうので，移動後の \(A'\) 点を頂点とする三角形分布を離散値で表現することは出来ません． これを，現存の格子点上で表現しようとすると, Figure 15 の青線のような図形になってしまって， 結果的にピークの \(A'\) 点は \(B_1\) 点と \(B_2\) 点のようにピークが減衰した形でしか表現出来ません． これは, 前章の「 風上差分と数値拡散 」で述べた数値拡散を図形的に説明したものとも言えます．

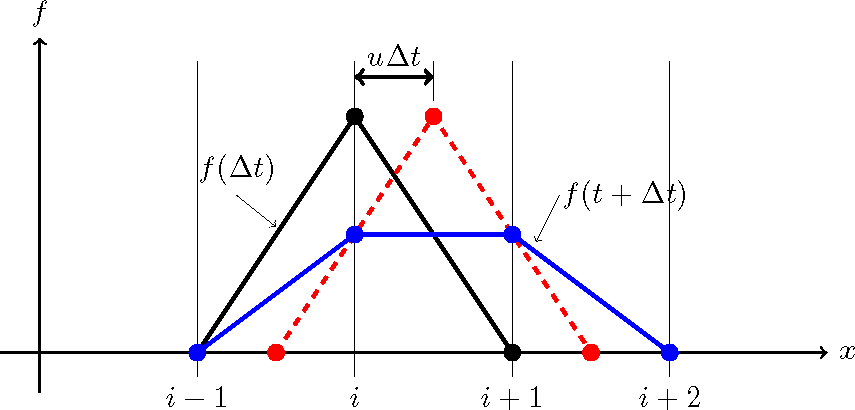
Figure 15 ::変数の移流(2)

以上の説明は，時刻が \(t\) から \(t+\Delta t\) に進む 時の説明でしたが，これを，時刻が \(t-\Delta t\) から \(t\) に進むとし場合に置き換えて見ましょう． Figure 16 に示すように, 時刻 \(t\) における \(f\) の分布が正しく \(A\) を 頂点とえうる三角形分布で表現される ためには，時刻 \(t-\Delta t\) における \(A'\) を頂点とする三角形分布が正しく表現されている必要があります． しかしながら, \(A'\) 点は格子点上に無いため，離散値でこの形を表現することは不可能です． そこで，時刻 \(t-\Delta t\) における分布形は離散値ではなく，何等かの連続関数である必要があります． これが，次に説明するCIP法の起源となります．

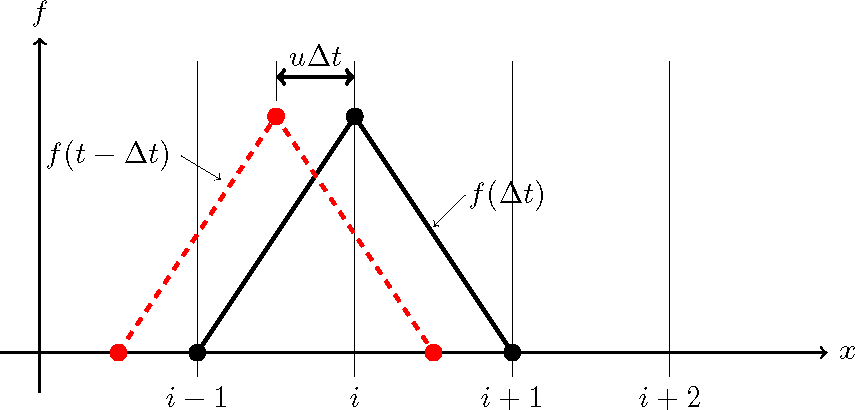
Figure 16 ::変数の移流(3)

CIP法 の基本概念

1次元移流方程式を再記します．

(24)\[\cfrac{\partial f}{\partial t}+u\cfrac{\partial f}{\partial x}=0\]

なお，前章の (1) では移流速度を \(c\) としていましたが， ここでは \(u\) としてあります．(特に意味も理由も無いのですが，流体の計算では移流速度は流体の流速 が用いられ，流速は \(u, v, w\) などが用いられる場合が多いのでここでは \(u\) としました．)

(24) 式の1次元移流方程式を数値的に計算するということは, 要するに \(f(x,t+\Delta t)\) をどう推定するかということです. 前節で説明したように，通常の風上差分ではこれを \(f(x-\Delta x,t)\) と \(f(x,t)\) を使って計算します．ただし，前記のようにこの方法は計算は安定ですが， 計算結果が拡散してしまって（数値拡散）正確ではありません． そこで，ここでは一次精度風上差分に代わる高精度の差分法である矢部ら [Ref:1] によって開発された CIP法 を紹介します．

そもそも (24) 式の意味するところは 変数 \(f\) の分布形を速度 \(u\) で伝えているのですから, \(\Delta t\) 時間の間には \(f\) の分布形が伝わる距離は \(u \Delta t\) のはずです. 即ち, 将来の \(f=f(x, t+\Delta t)\) は 現在の \(f=f(x-u\Delta t, t)\) がそのまま伝わっているはずです( Figure 17 参照).

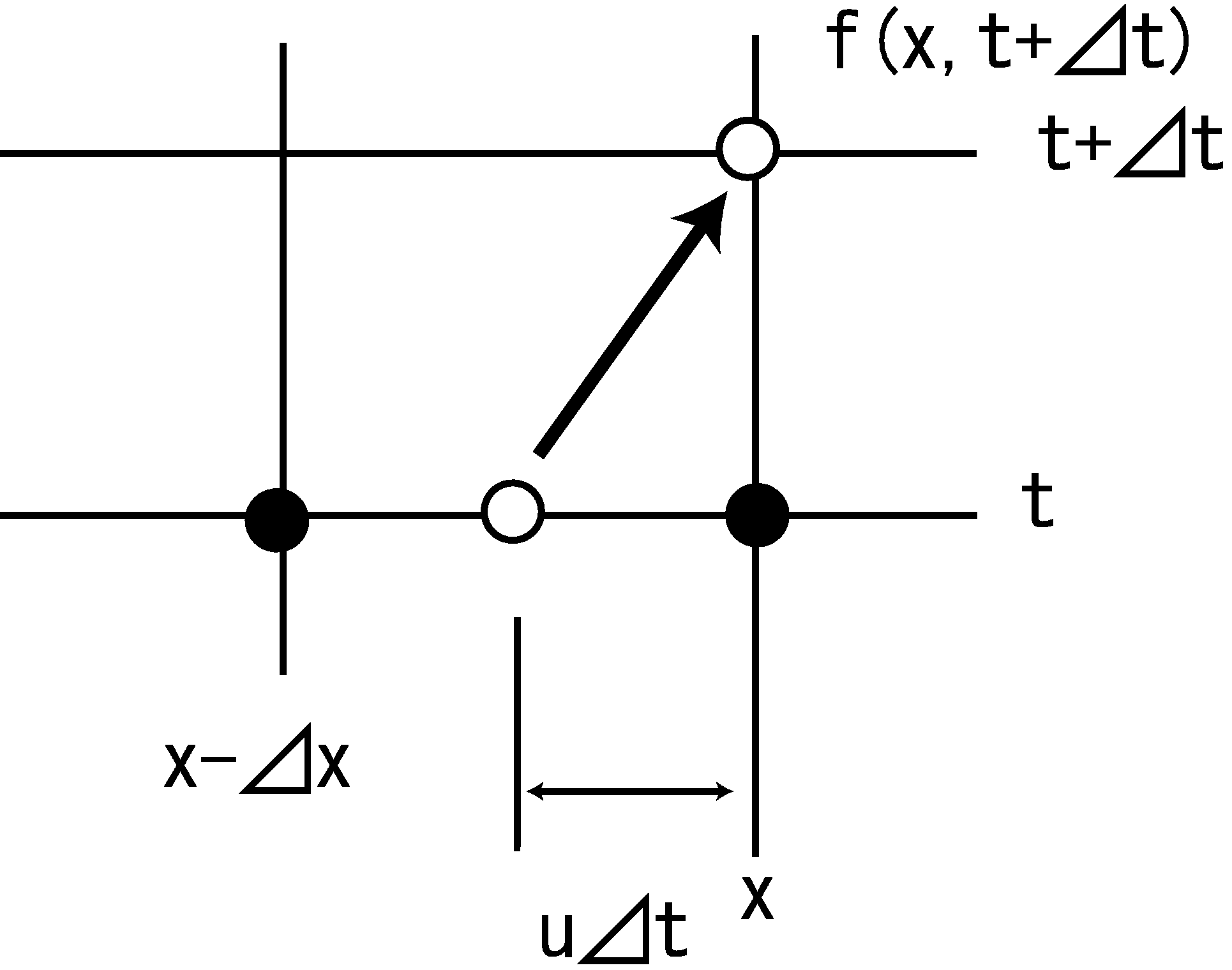
Figure 17 :\(f(x,t+\Delta t)\) の伝わり方

将来の \(f(x,t+\Delta t)\) を推定する代わりに, 現在の \(f(x-u\Delta t, t)\) が推定できれば, その値をそのまま用いることが可能となるわけです. これを式で書けば,

(25)\[f(x,t+\Delta t) \simeq f(x-u\Delta t, t)\]

となります.

格子間の変数分布形推定方法

3次関数の導入

\(f(x-u\Delta t, t)\) を推定する方法はいろいろあると思いますが, 問題は \(f\) は離散量として与えられているので, \(f\) の既知量は Figure 17 の●点であり, この2つの●の点から○の \(f(x-u\Delta t, t)\) を推定する必要があるということになります. 最も単純には2点間を直線で結んで比例配分するという方法でしょうが, 2点の間で \(f\) が急激に変化している場合や, 1度増加して減少する場合などを 考慮できるためには3次関数で表すのが妥当です.

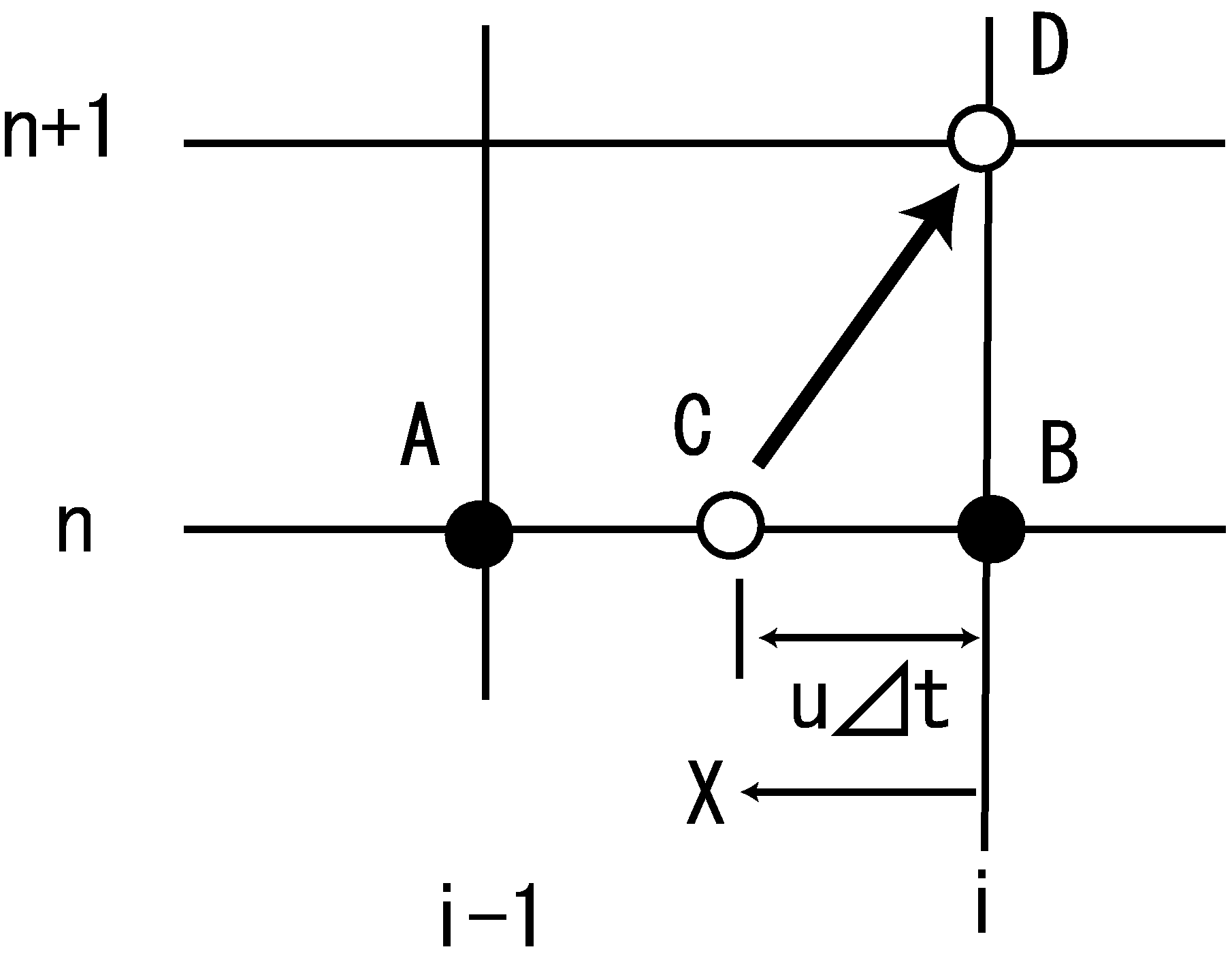
Figure 18 : CIP法の説明模式図

Figure 18 に示すように \(x\) 方向に \(i\) , \(t\) 方向に \(n\) で離散量を表し, A点およびB点における \(f\) を \(f(i-1,n)\) および \(f(i,n)\) とします. AB間における \(f\) の分布を3次関数で, \(X\) をBからAに向かった距離として表すと

(26)\[F=a_1 X^3 + a_2 X^2 + a_3 X + a_4\]

となり, \(a_1 \sim a_4\) の4個のパラメータを含む3次式となります. ここで注意して頂きたいのは，\(f\) は各格子点で定義される離散量であるのに 対して， \(F\) は各格子点の \(f\) を格子の間を補完する連続関数 (3次式)であるという点です． (26) 式中の4個の パラメータを決定するためには4つの条件が必要となります. このうち2つは,

(27)\[\begin{split}\mbox{B点で:} & F_{(X=0)}=f(i,n) \\ \mbox{A点で:} & F_{(X=\Delta x)} = f(i-1,n)\end{split}\]

の条件で決まりますが, あと2つはどうしたら良いでしょうか? これもいろいろ考えられます(たとえば, \(f(i-2,n)\) や \(f(i+1,n)\) などを用いる) がCIP法では, \(f\) の \(x\) 軸方向の勾配を用います. つまり,

(28)\[\begin{split}\mbox{B点で:} & \displaystyle{{\partial F}\over{\partial x}}_{(X=0)}= {{\partial f}\over{\partial x}} (i,n) \\ \mbox{A点で:} & \displaystyle{{\partial F}\over{\partial x}}_{(X=\Delta x)} = {{\partial f}\over{\partial x}}(i-1,n)\end{split}\]

(27) \(\sim\) (28) 式によって \(i\) と \(i-1\) の情報のみでAB間の \(f\) の分布 \(F\) が推定できることになり, これもCIP法の大きなメリットの一つです.

(26) 式およびこれを \(x\) で偏微分した,

(29)\[F_x= {{\partial F}\over{\partial x}} =3 a_1 X^2 + 2 a_2 X +a_3\]

に (27) \(\sim\) (28) 式の4つの条件を適用して, \(a_1 \sim a_4\) のパラメータを決定して \(F\) を求めれば良いのですが, これはちょっと面倒そうなので (27) \(\sim\) (28) 式の内, B点の条件( \(X=0\) )を自動的に満たす

(30)\[F(X)=\left[ (aX + b)X + f_x(i,n) \right] X + f(i,n)\]

をあらためて用いることとします. ただし,

(31)\[f_x(i,n) = \displaystyle{{\partial f}\over{\partial x}} (i,n)\]

です. (30) 式を書き直して,

(32)\[F(X)=aX^3+bX^2+f_x(i,n)X+f(i,n)\]

となり, これを \(x\) で偏微分すると,

(33)\[F_x(X)=3aX^2+2bX+f_x(i,n)\]

となります．

(32) 式と (33) 式は (27) 式と (28) 式のうちB点の条件( \(X=0\) )を自動的に満たしています． あとは，(27) 式と (28) 式のうちB点の条件( \(X=\Delta x\) ) を (32) 式と (33) 式に適用して,

(34)\[\begin{split}a\Delta x^3 + b \Delta x^2 + f_x(i,n) \Delta x + f(i,n) = f(i-1,n) \\ 3a\Delta x^2 + 2b\Delta x + f_x(i,n) = f_x(i-1,n)\end{split}\]

これより,

(35)\[\begin{split}a=\displaystyle{{ \left[(f_x(i-1,n)+f_x(i,n) \right] \Delta x + 2 \left[f(i,n)-f(i-1,n) \right] }\over{\Delta x^3}} \\ b=\displaystyle{{ 3\left[(f(i-1,n)-f(i,n) \right]- \left[f_x(i-1,n)+2f_x(i,n) \right] \Delta x }\over{\Delta x^2}}\end{split}\]

が求まります.

演習問題(1)

(35) 式の誘導をして下さい．

CIP法による格子間変数分布式の推定法のまとめ

以上をまとめると, (24) 式にCIP法を適用して \(f(x,t+\Delta t)\) を 求める手順は以下となります．

1. (35) 式で \(a, b\) を求める.

2. (30) 式に \(a, b\) を代入して, \(X=u\Delta t\) とすることで, \(F(X=u\Delta t)=f(x-u\Delta t, t)\) を求める．

3. 同時に \(F_x(X=u\Delta t)=f_x(x-u\Delta t, t)\) は (33) 式で求める．

4. (25) 式で \(f(x,t+\Delta t)\) を求める．

これを \(i=1 \sim N_i\) で実行し, 終了後に時間更新する.

Pythonコードと計算例

CIP法による1次元移流方程式の数値解法のPythonコードの例を https://github.com/YasuShimizu/Python-Code/blob/main/cip.py に示します．

この計算を実行すると，以下のような結果が得られます． ただし, \(x_b\) = 10, \(x_p\) = 10, \(f_p\) = 0.5, \(u\) = 0.5 としてあります．

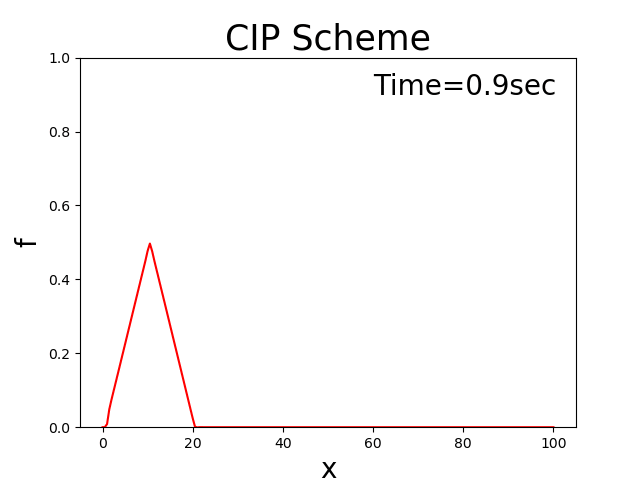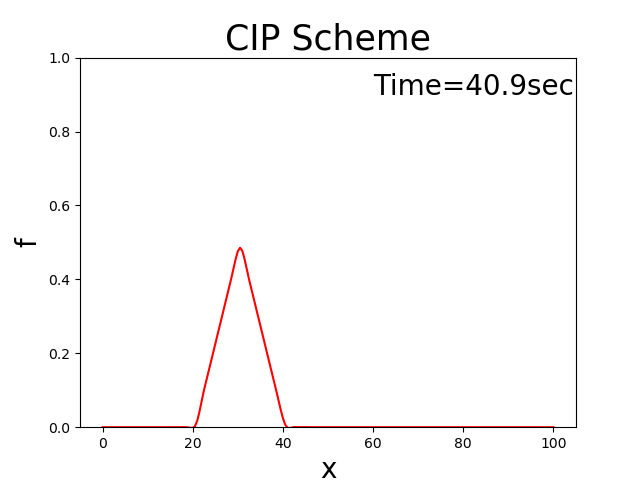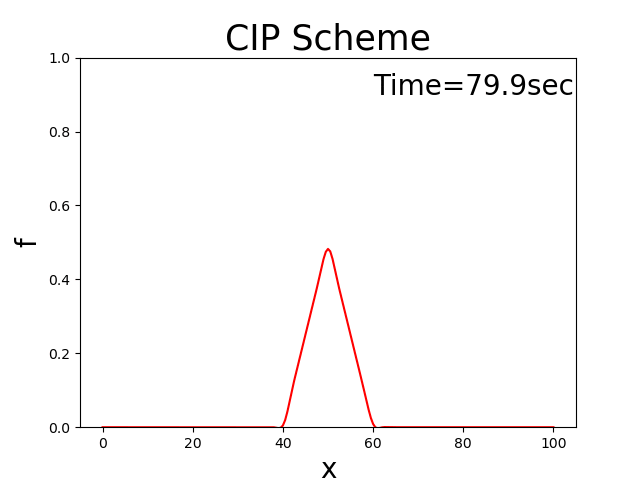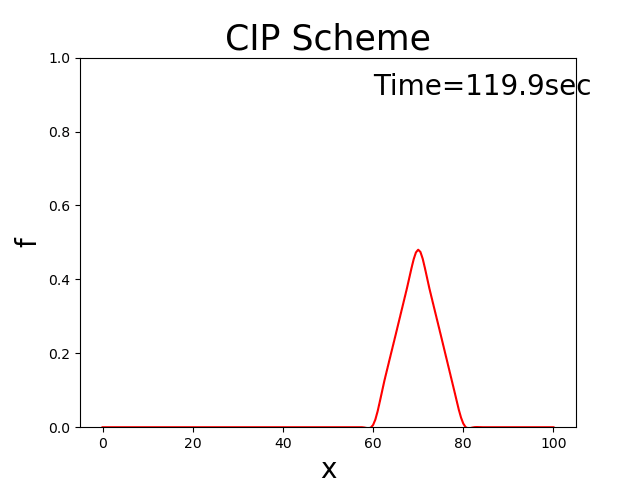
Figure 19 : 1次元移流方程式(CIP法)

このようにCIP法を用いると初期条件の三角形の分布系が崩れることなく，一定速度で 下流側に進んでいく様子が計算されていることが分かります． Appendixに掲載している理論解( Figure 142 )と比較してもほぼ同じ結果 が得られています．

移流方向が変化する移流方程式

前記の CIP法 の基本概念 では移流方向が一定である場合の計算法について述べましたが，ここでは移流方向が変化する 場合にいて述べます． 1次元の移流方程式 (24) 式において，これまでの説明では移流速度 \(u\) は一定 として扱って来ましたが， ここでは \(u\) は一定ではなく，時間・空間的に変化する可変量とします．一般に流体では \(u\) は流れの向きに よって正だったり負だったりしますので， \(u>0\) でも \(u<0\) でも対応可能なアルゴリズムを用意 する必要があります．

u<0 の場合

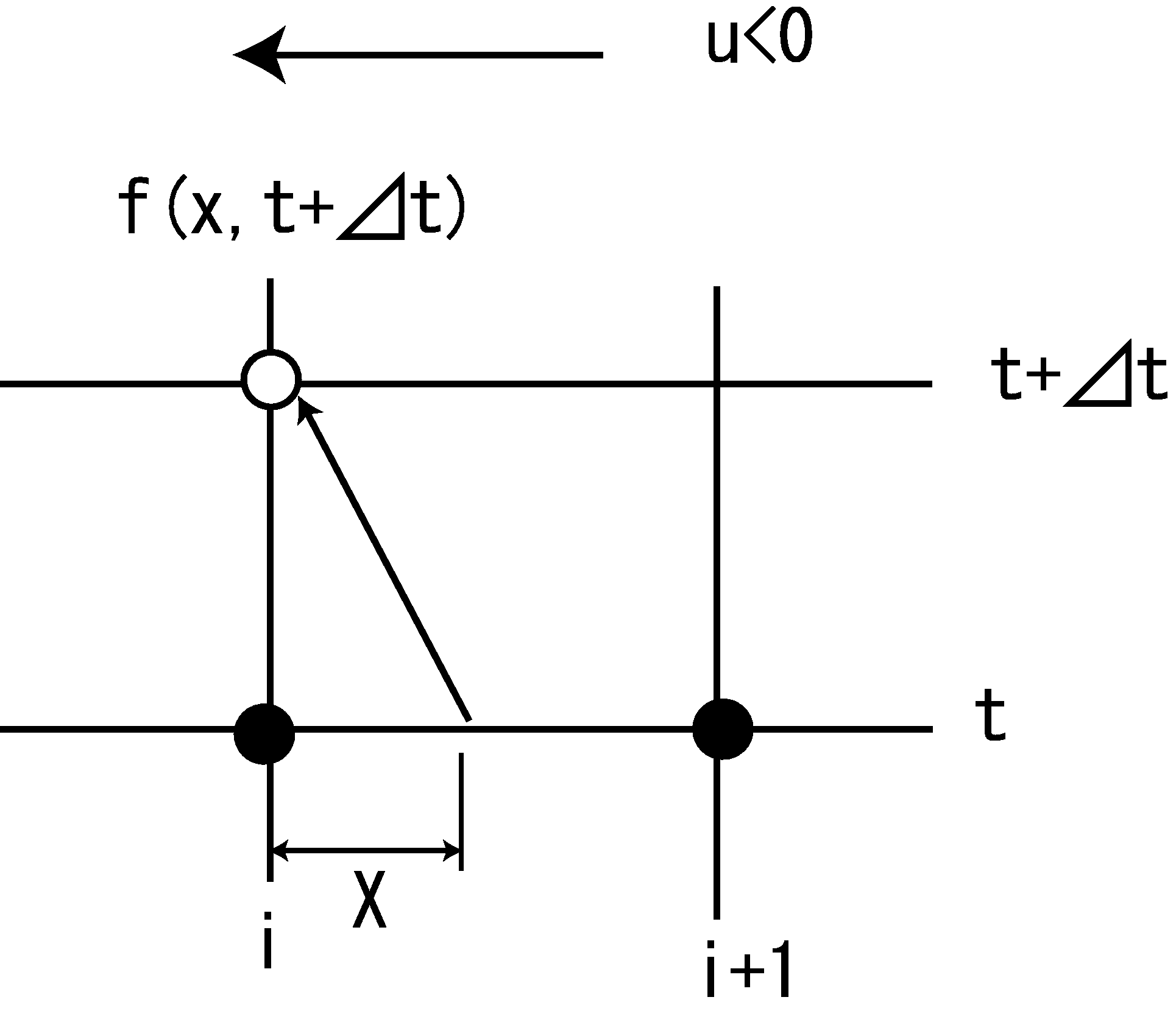
Figure 20 : \(u<0\) の場合の模式図

上図のように \(u<0\) の場合

(36)\[X=-u\Delta t\]

とおいて，\(i\) と \(i+1\) の間の \(f\) の分布を次式で表します. ただし \(X>0\) です．

(37)\[F(X)=\left[ (aX + b)X + f_x(i) \right] X + f(i)\]

また, \(F(X)\) の微分量は,

(38)\[F'(X)=3aX^2+2bX+f_x(i)\]

ここで, \(f_x\) は

(39)\[f_x = {{\partial f}\over{\partial x}}\]

のことです. \(F\) および \(F'\) は

(40)\[\begin{split}X=0 \mbox{で:} & F(X)=f(i) \mbox{および} F'(X)=f_x(i) \\ X=\Delta x \mbox{で:} & F(X)=f(i+1) \mbox{および} F'(X)=f'(i+1)\end{split}\]

の条件より,

(41)\[\begin{split}a=\displaystyle{{ \left[(f_x(i+1)+f_x(i) \right] \Delta x + 2 \left[f(i)-f(i+1) \right] }\over{\Delta x^3}} \\ b=\displaystyle{{ 3\left[(f(i+1)-f(i) \right]- \left[f_x(i+1)+2f_x(i) \right] \Delta x }\over{\Delta x^2}}\end{split}\]

が得られます.

演習問題(2)

(41) 式の誘導をして下さい．

u>0 の場合

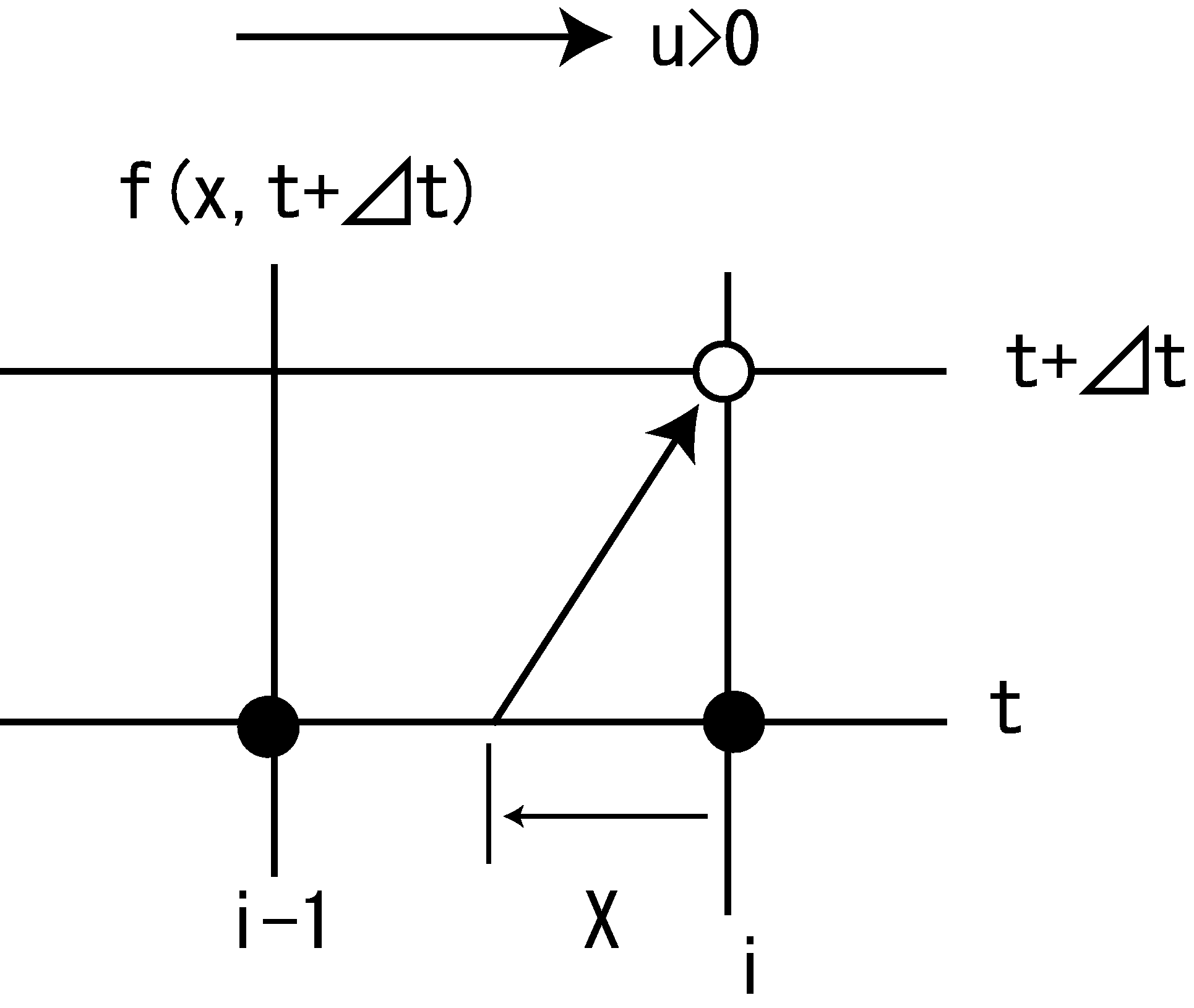
Figure 21 : \(u>0\) の場合の模式図

上図のように \(u>0\) の場合も

(42)\[X = - u \Delta t\]

と起きます. 前節では \(X = u \Delta t (>0)\) としましたが, ここでは (42) 式のように \(X<0\) となるように設定します. この理由はあとで分かりますが, \(u<0\) でも \(u>0\) でも同じアルゴリズムを使用可能とするためのものです. \(u>0\) の場合には, \(i\) と \(i-1\) の間の \(f\) の分布を次式で表します. これは (37) 式と全く同じ形です.

(43)\[F(X)=\left[ (aX + b)X + f_x(i) \right] X + f(i)\]

また, \(F(X)\) の微分量は,

(44)\[F'(X)=3aX^2+2bX+f_x(i)\]

で表されます. \(F\) および \(F'\) は

(45)\[\begin{split}X=0 \mbox{で: } & F(X)=f(i) \mbox{および} F'(X)=f_x(i) \\ X= -\Delta x \mbox{で: } & F(X)=f(i-1) \mbox{および} F'(X)=f'(i-1)\end{split}\]

の条件より,

(46)\[\begin{split}a=\displaystyle{{ \left[(f_x(i-1)+f_x(i) \right] \Delta x - 2 \left[f(i)-f(i-1) \right] }\over{\Delta x^3}} \\ b=\displaystyle{{ 3\left[(f(i-1)-f(i) \right]+ \left[f_x(i-1)+2f_x(i) \right] \Delta x }\over{\Delta x^2}}\end{split}\]

が得られます.

演習問題(3)

(46) 式の誘導をして下さい．

u>0 でも u<0 でも使えるようにするには?

(41) 式が \(u<0\) の場合で, (46) 式が \(u>0\) の場合ですが, これらのペアを比べてみると, 大変良く似ています. そこで，

(47)\[\begin{split}\mbox {sign}(Y) & =1 & ,Y>0 \\ \mbox {sign}(Y) & =-1 & ,Y<0\end{split}\]

で定義されるsign関数(シグナル関数もしくは符号関数とも呼ばれます)を利用して，

(48)\[i_m = i - \mbox{sign}(u)\]

という \(i_m\) を定義すると,

(49)\[\begin{split}u>0 \mbox{のとき} i_m & = i-1 \\ u<0 \mbox{のとき} i_m & = i+1\end{split}\]

となります. したがって, (41) 式および (46) 式の代わりに,

(50)\[\begin{split}a=\displaystyle{{ \left[(f_x(i_m)+f_x(i) \right] \Delta x \cdot \mbox{sign}(u)- 2 \left[f(i)-f(i_m) \right] }\over{\Delta x^3 \cdot \mbox{sign}(u)}}\\ b=\displaystyle{{ 3\left[(f(i_m)-f(i) \right]+ \left[f_x(i_m)+2f_x(i) \right] \Delta x \cdot \mbox{sign}(u)}\over{\Delta x^2}}\end{split}\]

とすることで, \(u<0\) の場合も \(u>0\) の場合も同じ式を用いることが出来ます．

例題

移流速度 \(u\) が次式で表されるような正負に単振動する場合の1次元移流方程式をCIP法で計算してみましょう．

初期条件は Figure 5 と同じとします．

(51)\[u=u_0 \sin \left( \cfrac{2\pi}{T_l} t \right)\]

ただし, \(u_0\) は振動流速の最大値，\(T_l\) は振動流速の周期である．

Pythonコードと計算例

移流方向が正負に振動する場合の移流方程式の CIP法に数値解法のPythonコードの例を

https://github.com/YasuShimizu/Python-Code/blob/main/cip_pm.py

に示します． このコードで，\(u_0\) =2.0, \(T_l\) =100 \(x_b\) = 10, \(x_p\) = 20, \(f_p\) = 0.5とした場合の計算結果を Figure 22 に示します．

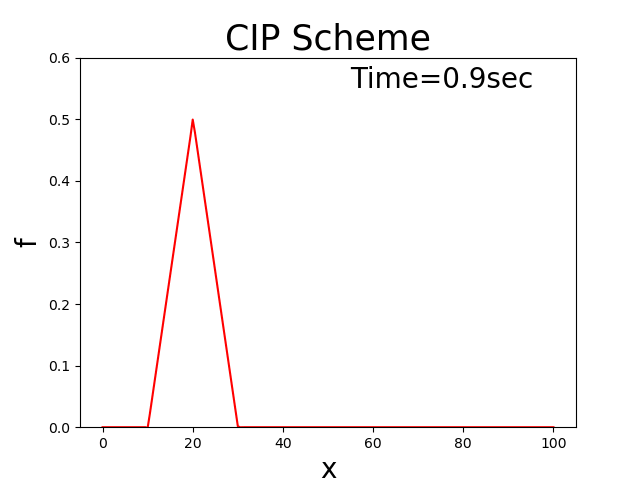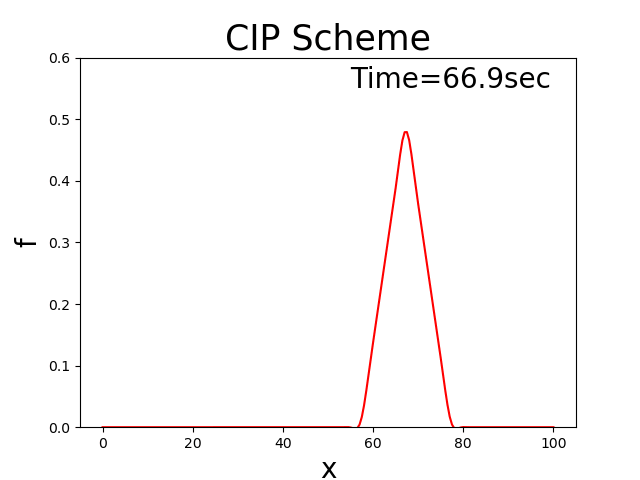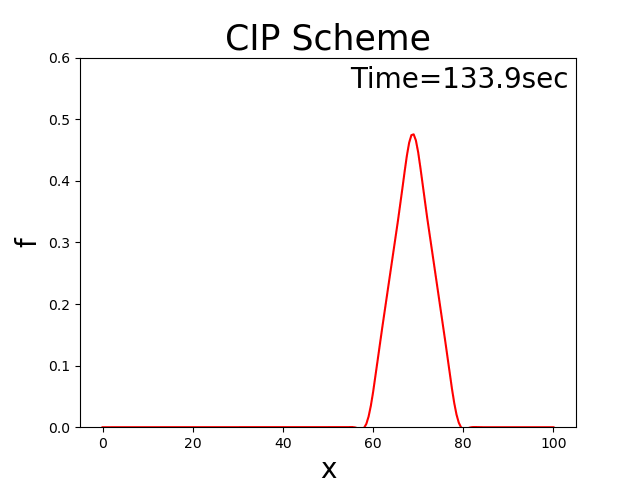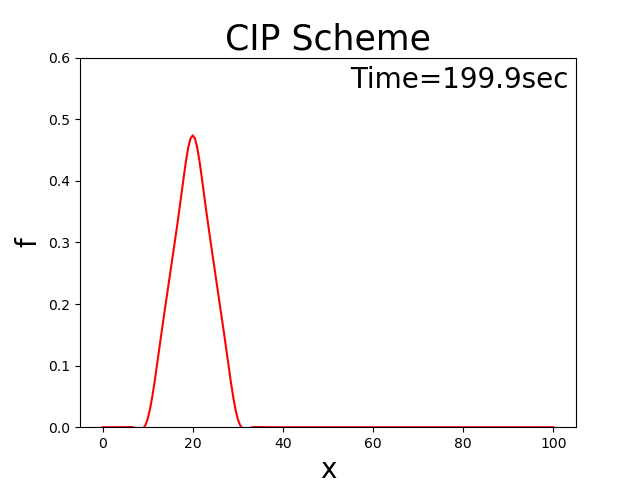
Figure 22 : 移流速度が正負振動する場合の計算結果

Source項を含む移流方程式

ここでは, 流体の数値計算を行う場合に不可欠となる分離解法の説明を行います. 流体の方程式の多くは, (24) 式のように右辺がゼロの場合は稀で, 多くは 右辺に値を持ちます. これを一般的に次式で表します.

(52)\[\cfrac{\partial f}{\partial t}+u\cfrac{\partial f}{\partial x}=G\]

\(G\) は流れの運動方程式の場合, 水面勾配, 河床勾配, 摩擦など様々 外力項(Source項)となりますが, 要するに移流項以外の成分のことです.

(52) 式を便宜的に以下の2つの式に分けます.

(53)\[{{\partial f}\over{\partial t}} = G\]

(54)\[{{\partial f}\over{\partial t}}+u{{\partial f}\over{\partial x}} = 0\]

\(f(t)\) および \(f(t+\Delta t)\) をそれぞれ \(f^n\) および \(f^{n+1}\) とし, (52) 式で \(f^n \rightarrow f^{n+1}\) を計算するのを, 一旦 (53) 式で \(f^n \rightarrow \widetilde{f}\) の計算を行い, さらに (54) 式で \(\widetilde{f} \rightarrow f^{n+1}\) を計算するというように 2段階で計算します. これを分離解法と言います. このように分離 することによって初めて (54) 式の形でCIP法が使えるようになります. この2段階はNon-Advection Phaseおよび, Advection Phaseと呼ばれます.

CIP法では, \(f\) の時間変化の他に (50) 式に表れる \(f_x\) 即ち空間微分量も 常に必要となるため, 微分量も同時に, Non-Advecion Phaseで \(\displaystyle{{{\partial f}\over{\partial x}}^n \rightarrow \widetilde{{\partial f}\over{\partial x}}}\), Advecion Phaseで \(\displaystyle{\widetilde{{\partial f}\over{\partial x}} \rightarrow {{\partial f}\over{\partial x}}^{n+1}}\) というように分離して計算します．

以上を整理すると以下のようになります.

Table 2 分離解法

Phase名	使用する数式	\(f\) の更新	\(\cfrac{\partial f}{\partial x}\) の更新
[A] Non-advection Phase	\(\displaystyle{{\partial f}\over{\partial t}}=G\)	(a) \(f^n \rightarrow \widetilde{f}\)	(b) \(\displaystyle{{{\partial f}\over{\partial x}}^n \rightarrow \widetilde{{\partial f}\over{\partial x}}}\)
[B] Advection Phase	\(\displaystyle{{{\partial f}\over{\partial t}}+u{{\partial f}\over{\partial x}}}=0\)	(c) \(\widetilde{f} \rightarrow f^{n+1}\)	(d) \(\displaystyle{\widetilde{{\partial f}\over{\partial x}} \rightarrow {{\partial f}\over{\partial x}}^{n+1}}\)

以上のように分離した方程式を用いてそれぞれの段階での計算方法を以下に 示します. なお以下の説明においては移流項以外を差分表示する必要が ある場合は, 出来るだけ精度の高い中央差分を用いることととします.

Non-Advection Phase

(53) 式より

(55)\[{{\widetilde{f}-f^n}\over{\Delta t}} = G^n\]

(56)\[\widetilde{f} = f^n +G^n \Delta t\]

計算点を \(i\) とすると,

(57)\[\widetilde{f}(i) = f^n(i) +G^n(i) \Delta t\]

でNon-Advection Phaseの \(f\) が更新されます( \(f^n \rightarrow \widetilde{f}\) ).

(56) の両辺を \(x\) で微分して,

(58)\[\widetilde{{\partial f}\over{\partial x}} ={{\partial f}\over{\partial x}}^n +{{\partial G}\over{\partial x}}^n \Delta t\]

上式の \(\displaystyle{{{\partial G}\over{\partial x}}^n}\) を中央差分で表すと,

(59)\[\widetilde{{\partial f}\over{\partial x}} ={{\partial f}\over{\partial x}}^n +{{G^n(i+1)-G^n(i-1)}\over{2\Delta x}} \Delta t\]

ここで, (57) 式より,

(60)\[\begin{split}G^n(i+1)={{\widetilde{f}(i+1)-f^n(i+1)}\over{\Delta t}} \\ G(i-1)={{\widetilde{f}(i-1)-f^n(i-1)}\over{\Delta t}}\end{split}\]

なので, (60) を (59) に代入して,

(61)\[\widetilde{{\partial f}\over{\partial x}}(i)={{\partial f}\over{\partial x}}^n(i)+{{1}\over{2\Delta x}} \left[\widetilde{f}(i+1)-f^n(i+1)-\widetilde{f}(i-1)+f^n(i-1)\right]\]

となります. したがって, Non-Advection Phaseにおける変数 \(f\) および その空間微分量 \(\displaystyle{{{\partial f}\over{\partial x}}}\) の更新は, 表 Table 2 中の(a)の部分は (57) 式で,表 Table 2 中の(b)の部分は (61) 式で求めることが出来ます.

Advection Phase

変数 \(f`の更新は表 :numref:`bunri_hyo\) 中の(c)の部分で行いますが， これは今まで解説してきたCIP法をそのまま適用できます. 即ち (37) 式または (43) 式(同じものですが)を適用して,

(62)\[{f(i)}^{n+1}=F(X)= \left[(aX+b)X+ \widetilde{{\partial f}\over{\partial x}}(i) \right] X +\widetilde{f}(i)\]

ただし, \(a\) および \(b`は :eq:`ab\) 式で与えられます.

次にAdvection Phaseにおける空間微分量 \(\displaystyle{{\partial f}\over{\partial x}}\) の更新法を考えて見ます[表 Table 2 中の(d)の部分]. (54) 式の両辺を \(x\) で偏微分します.

(63)\[{{\partial \over \partial x}}\left( {{\partial f}\over{\partial t}} \right) + {{\partial \over \partial x}} \left( u {{\partial f}\over{\partial x}} \right) =0\]

ここで \(\displaystyle{{\partial f}\over{\partial x}}\) を \(f'\) と 置いて第2項目を展開すると,

(64)\[{{\partial f'}\over{\partial t}} + u{{\partial f'}\over{\partial x}} = -{{\partial u}\over{\partial x}} f'\]

となります.いまここで考えているのは, Advection Phaseでの \(\displaystyle{{\partial f}\over{\partial x}}\) の更新ですので, この式を用いて, \(\widetilde{f'} \rightarrow {f'}^{n+1} \left( \displaystyle{ \widetilde{{\partial f}\over{\partial x}} \rightarrow {{\partial f}\over{\partial x}}^{n+1}} \right)\) を行えば良いことになります.

ここで，(63) 式と (52) 式を比べてみましょう. (64) 式は (52) 式で \(f\) を \(f'\) に, \(G\) を \(\displaystyle{-{{\partial u}\over{\partial x}} f'}\) としたものに一致しています. そこで (52) 式でやったのと同じように (63) 式に対して分離解法を適用します. 即ち, (63) を

(65)\[{{\partial f'}\over{\partial t}} + u{{\partial f'}\over{\partial x}} = 0\]

(66)\[{{\partial f'}\over{\partial t}} = -{{\partial u}\over{\partial x}} f'\]

のように分離して, \(\widetilde{f'}\) と \({f'}^{n+1}\) の間に中間量として \(\widehat{f'}\) を考え, (65) 式で \(\widetilde{f'} \rightarrow \widehat{f'}\) を, (66) 式で \(\widehat{f'} \rightarrow {f'}^{n+1}\) を計算することにします.

まず (65) 式ですが, これに再度CIP法を適用するのも一つの方法ですが, CIP法で用いられる \(F(X)\) の空間微分量である (38) 式または (44) 式(どちらも同じ形です)の \(F'(X)\) を用いる方が賢明のようです. 即ち,

(67)\[\widehat{f'}(i) = \widetilde{F'}(X)\]

として,

(68)\[\widehat{f'}(i) = 3aX^2 + 2bX + \widetilde{f'}(i)\]

で計算します. (66) 式のほうは,

(69)\[{{{f'}^{n+1}(i) - \widehat{f'}(i)}\over{\Delta t}} = - {{u(i+1)-u(i-1))}\over{2\Delta x}} \widehat{f'}(i)\]

と中央差分を適用し, これより

(70)\[{f'}^{n+1}(i) = \widehat{f'}(i) -{{u(i+1)-u(i-1))}\over{2\Delta x}} \widehat{f'}(i) \Delta t\]

で計算します.

演習問題(4)

(52) 式の右辺 \(G\) が \(\displaystyle{D{{\partial^2 f}\over{\partial x^2}}}\) のとき,

\[\displaystyle{{{\partial f}\over{\partial t}}+u{{\partial f}\over{\partial x}}= D{{\partial^2 f}\over{\partial x^2}}}\]

のような移流 \(\cdot\) 拡散方程式となります. これを分離解法で計算する方法について述べよ.

Pythonコードと計算例

移流拡散方程式の計算用Pythonコードの例を

https://github.com/YasuShimizu/Python-Code/blob/main/cip_pm_diffusion.py

に示します． このコードで拡散係数 \(D=0.5\) , \(u_0\) =2.0, \(T_l\) =100 と した場合の計算結果を Figure 23 に示します．左右に移動しながら最初は三角形の分布形状が 徐々に拡散していく様子が表わされています．

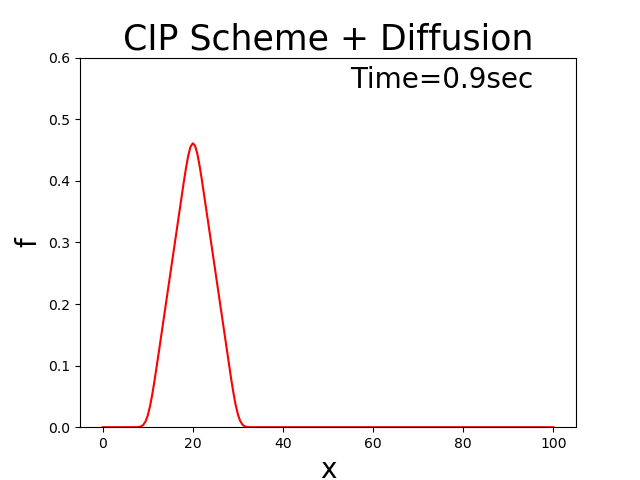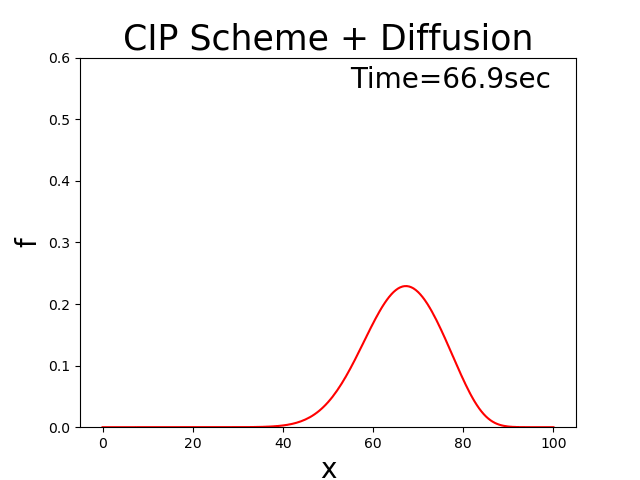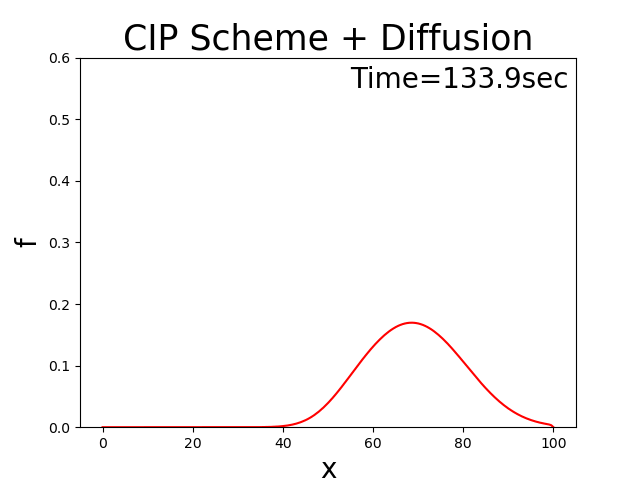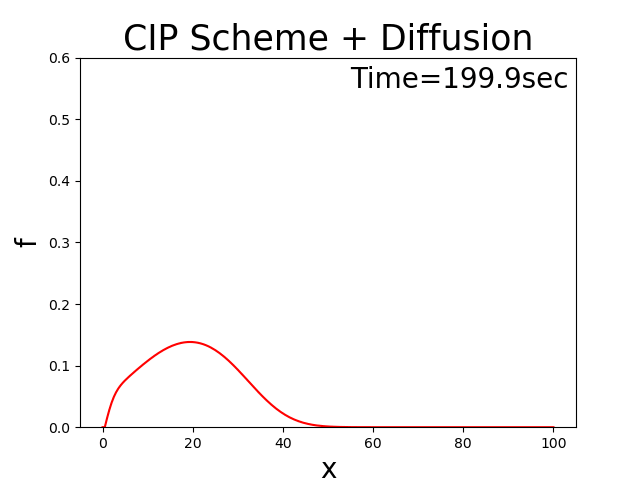
Figure 23 : 移流速度が正負振動する場合の移流拡散方程式計算結果

なお，移流項の高精度差分法はCIP法以外にも数多く提案されており，そのうちいくつかを，Appendix ( 他の移流項高精度差分法) で紹介しておきます．