Conversion of the basic 2D flow equations to the s-n coordinates
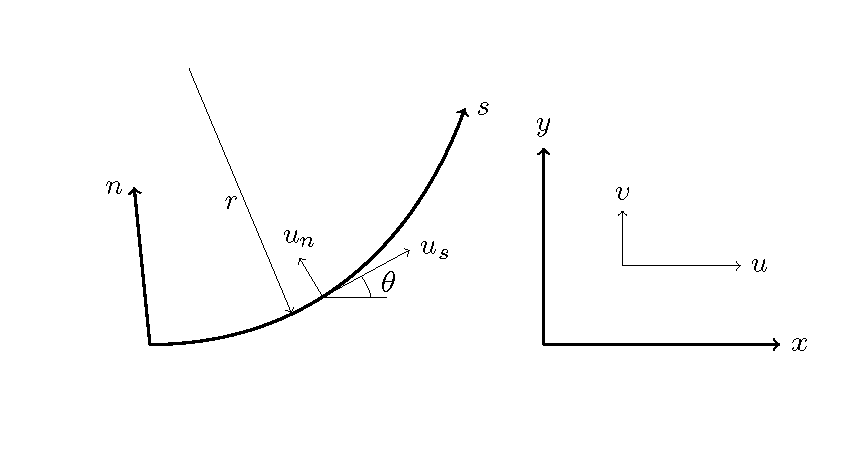
Let us assume that the \(s-n\) coordinates are Cartesian curvilinear coordinates. On the \(s-n\) coordinates, the \(s\) axis is an arbitrary curve, and the \(n\) axis is a straight coordinate axis perpendicular to the s axis.
Figure 11 : The \(x-y\) coordinate and the \(s-n\) coordinate
As shown in Figure 11 \(x-y\) coordinates, let the flow velocity in the \(x\) axis direction be u and the flow velocity in the \(y\) axis direction be \(v\) , and for the \(s-n\) coordinates, let the flow velocity in the \(s\) axis direction be u_s and the flow velocity in the \(n\) axis direction be \(u_n\) . Also, let the angle between the \(s\) axis and the \(x\) axis be \(\theta\) , and the radius of curvature of the \(s\) axis be \(r\) .
As shown in Figure 11 \(r\) is positive for a curvature whose \(\theta\) increases in the positive direction of the \(s\) axis.
From the definition of the curvature,
(73) \[r d\theta = ds, \; \; \cfrac{\partial \theta}{\partial s}= \cfrac{1}{r}, \; \;
\cfrac{\partial \theta}{\partial n}=0\]
\(u,v\) and \(u, v\) have the following relationships.
(74) \[\begin{split}u=u_s \cos \theta - u_n \sin \theta \\
v=u_s \sin \theta + u_n \cos \theta\end{split}\]
(75) \[\begin{split}u_s=u \cos \theta + v \sin \theta \\
u_n=-u \sin \theta + v \cos \theta\end{split}\]
Each partial derivative has the following relationship.
(76) \[\begin{split}\left( \begin{array}{c}
\cfrac{\partial}{\partial x} \\
\\
\cfrac{\partial}{\partial y}
\end{array} \right)
=
\left( \begin{array}{cc}
\cos{\theta} & -\sin{\theta} \\
\\
\sin{\theta} & \cos{\theta}
\end{array} \right)
\left( \begin{array}{c}
\cfrac{\partial}{\partial s} \\
\\
\cfrac{\partial}{\partial n}
\end{array} \right)\end{split}\]
(77) \[\begin{split}\left( \begin{array}{c}
\displaystyle{{\partial}\over{\partial s}} \\
\\
\displaystyle{{\partial}\over{\partial n}}
\end{array} \right)
=
\left( \begin{array}{cc}
\cos{\theta} & \sin{\theta} \\
\\
-\sin{\theta} &
\cos{\theta}
\end{array} \right)
\left( \begin{array}{c}
\displaystyle{{\partial}\over{\partial x}} \\
\\
\displaystyle{{\partial}\over{\partial y}}
\end{array} \right)\end{split}\]
Also,
(78) \[\cfrac{\partial s}{\partial x}=\cos \theta, \; \;
\cfrac{\partial s}{\partial y}=\sin \theta, \; \;
\cfrac{\partial n}{\partial x}=-\sin \theta, \; \;
\cfrac{\partial n}{\partial y}=\cos \theta\]
Equation of continuity
(79) \[\cfrac{\partial h}{\partial t}
+\cfrac{\partial (hu)}{\partial x}
+\cfrac{\partial (hv)}{\partial y}=0\]
(80) \[\cfrac{\partial h}{\partial t}
+\cfrac{\partial}{\partial x}
\left\{ h(u_s \cos \theta - u_n \sin \theta) \right\}
+\cfrac{\partial}{\partial y}
\left\{ h(u_s \sin \theta + u_n \cos \theta) \right\}=0\]
(81) \[\begin{split}\cfrac{\partial h}{\partial t}
+\cos \theta \cfrac{\partial}{\partial s}
\left\{ h(u_s \cos \theta - u_n \sin \theta) \right\}
-\sin \theta \cfrac{\partial}{\partial n}
\left\{ h(u_s \cos \theta - u_n \sin \theta) \right\} \\
+\sin \theta \cfrac{\partial}{\partial s}
\left\{ h(u_s \sin \theta + u_n \cos \theta) \right\}
+\cos \theta \cfrac{\partial}{\partial n}
\left\{ h(u_s \sin \theta + u_n \cos \theta) \right\}=0\end{split}\]
(82) \[\begin{split}\cfrac{\partial h}{\partial t}
+\cos \theta \left\{
\cos\theta \cfrac{\partial(h u_s)}{\partial s}+h u_s \cfrac{\partial \cos \theta}{\partial s}
-\sin\theta \cfrac{\partial(h u_n)}{\partial s}-h u_n \cfrac{\partial \sin \theta}{\partial s}
\right\} \\
-\sin \theta \left\{
\cos\theta \cfrac{\partial(h u_s)}{\partial n}+h u_s \cancelto{0}{\cfrac{\partial \cos \theta}{\partial n}}
-\sin\theta \cfrac{\partial(h u_n)}{\partial n}-h u_n \cancelto{0}{\cfrac{\partial \sin \theta}{\partial n}}
\right\} \\
+\sin \theta \left\{
\sin\theta \cfrac{\partial(h u_s)}{\partial s}+h u_s \cfrac{\partial \sin \theta}{\partial s}
+\cos\theta \cfrac{\partial(h u_n)}{\partial s}+h u_n \cfrac{\partial \cos \theta}{\partial s}
\right\} \\
+\cos \theta \left\{
\sin\theta \cfrac{\partial(h u_s)}{\partial n}+h u_s \cancelto{0}{\cfrac{\partial \sin \theta}{\partial n}}
+\cos\theta \cfrac{\partial(h u_n)}{\partial n}+h u_n \cancelto{0}{\cfrac{\partial \cos \theta}{\partial n}}
\right\}\end{split}\]
(83) \[\begin{split}\cfrac{\partial h}{\partial t}
+\cos^2\theta\cfrac{\partial(hu_s)}{\partial s} \cancel{-\cos\theta\sin\theta hu_s\cfrac{\partial\theta}{\partial s}}
\cancel{-\cos\theta\sin\theta\cfrac{\partial(hu_n)}{\partial s}}-\cos^2\theta hu_n\cfrac{\partial\theta}{\partial s} \\
\cancel{-\sin\theta\cos\theta\cfrac{\partial(hu_s)}{\partial n}}
+\sin^2\theta\cfrac{\partial(hu_n)}{\partial n} \\
+\sin^2\theta\cfrac{\partial(hu_s)}{\partial s} +\cancel{\sin\theta\cos\theta hu_s\cfrac{\partial\theta}{\partial s}}
\cancel{+\sin\theta\cos\theta\cfrac{\partial(hu_n)}{\partial s}}-\sin^2\theta hu_n\cfrac{\partial\theta}{\partial s} \\
\cancel{+\cos\theta\sin\theta\cfrac{\partial(hu_s)}{\partial n}}
+\cos^2\theta\cfrac{\partial(hu_n)}{\partial n}\end{split}\]
(84) \[\begin{split}\cfrac{\partial h}{\partial t}
+(\cos^2\theta+\sin^2\theta)\cfrac{\partial(hu_s)}{\partial s}
-(\cos^2\theta+\sin^2\theta)hu_n\cfrac{\partial\theta}{\partial s} \\
+(\cos^2\theta+\sin^2\theta)\cfrac{\partial(hu_n)}{\partial n} =0\end{split}\]
(85) \[\cfrac{\partial h}{\partial t}
+\cfrac{\partial(hu_s)}{\partial s}-\cfrac{hu_n}{r}
+\cfrac{\partial(hu_n)}{\partial n} =0\]
Where,
(86) \[\begin{split}\cfrac{\partial(rhu_n)}{\partial n}=r\cfrac{\partial(hu_n)}{\partial n}
+hu_n\cfrac{\partial r}{\partial n} \\
= r\cfrac{\partial(hu_n)}{\partial n}-hu_n\end{split}\]
Finally, the equation of continuity on the \(s-n\) axis is…
(87) \[\cfrac{\partial h}{\partial t}
+\cfrac{\partial(hu_s)}{\partial s}
+\cfrac{1}{r}\cfrac{\partial(rhu_n)}{\partial n} =0\]
Momentum equation
Let us review the equations of motion for the \(x-y\) axis.
(88) \[\frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}+
v \frac{\partial u}{\partial y}=
-g \frac{\partial H}{\partial x}
-\frac{\tau_x}{\rho h}+D_x\]
(89) \[\frac{\partial v}{\partial t}+u \frac{\partial v}{\partial x}+
v \frac{\partial v}{\partial y}=
-g \frac{\partial H}{\partial y}
-\frac{\tau_y}{\rho h}+D_y\]
Where, \(x, y\) are plane coordinate axes that are mutually perpendicular, \(t\) is time, \(u, v\) are the depth-averaged velocity in the \(x, y\) directions, \(h\) is the water depth, \(H\) is the water level, \(g\) is the gravitational acceleration, \(\tau_x, \tau_y\) are the riverbed shear force in the directions of \(x, y\) , \(\rho\) is the density of water and \(D_x, D_y\) are the diffusion term in the \(x, y\) directions.
Then, Equation (88) and Equation (89) are expressed as follows.
(90) \[\begin{split}A_x = P_x + F_x + D_x\\
A_y = P_y + F_y + D_x\end{split}\]
Where, \(A_x, A_y, P_x, P_y, F_x, F_y, D_x, D_y\) respectively express the advection term (acceleration term), the pressure gradient term, the friction term, and the diffusion terms in the directions of \(x, y\) .
By changing the subscript of each term to \(s,n\) , we have each term in the \(s,n\) axis directions.
The advection terms
Acceleration in the \(x, y\) directions can be written as follows:
(91) \[\begin{split}A_x = {{\partial u}\over{\partial t}}
+u{{\partial u}\over{\partial x}}
+v{{\partial u}\over{\partial y}}
={{\partial u}\over{\partial t}}
+u\left(
\cos\theta{{\partial u}\over{\partial s}}
-\sin\theta{{\partial u}\over{\partial n}} \right)
+v\left(
\sin\theta{{\partial u}\over{\partial s}}
+\cos\theta{{\partial u}\over{\partial n}} \right) \\
={{\partial u}\over{\partial t}}+
{{\partial u}\over{\partial s}}
\underbrace{(u\cos\theta+v\sin\theta)}_{u_s}
+{{\partial u}\over{\partial n}}
\underbrace{(-u\sin\theta+v\cos\theta)}_{u_n}
={{\partial u}\over{\partial t}}+
u_s{{\partial u}\over{\partial s}}
+u_n{{\partial u}\over{\partial n}}\end{split}\]
(92) \[\begin{split}A_y = {{\partial v}\over{\partial t}}
+u{{\partial v}\over{\partial x}}
+v{{\partial v}\over{\partial y}}
={{\partial u}\over{\partial t}}
+u\left(
\cos\theta{{\partial v}\over{\partial s}}
-\sin\theta{{\partial v}\over{\partial n}} \right)
+v\left(
\sin\theta{{\partial v}\over{\partial s}}
+\cos\theta{{\partial v}\over{\partial n}} \right) \\
={{\partial v}\over{\partial t}}+
{{\partial v}\over{\partial s}}
\underbrace{(u\cos\theta+v\sin\theta)}_{u_s}
+{{\partial v}\over{\partial n}}
\underbrace{(-u\sin\theta+v\cos\theta)}_{u_n}
={{\partial u}\over{\partial t}}+
u_s{{\partial v}\over{\partial s}}
+u_n{{\partial v}\over{\partial n}}\end{split}\]
Acceleration along the channel downstream direction
Then the acceleration in the \(s\) directions becomes:
(93) \[ \begin{align}\begin{aligned}A_s = & A_x\cos\theta+A_y\sin\theta
=\left(
{{\partial u}\over{\partial t}}+
u_s{{\partial u}\over{\partial s}}
+u_n{{\partial u}\over{\partial n}}
\right)\cos\theta+
\left(
{{\partial v}\over{\partial t}}+
u_s{{\partial v}\over{\partial s}}
+u_n{{\partial v}\over{\partial n}}
\right)\sin\theta\\= &\cos\theta{{\partial u}\over{\partial t}}
+
\cos\theta u_s {{\partial}\over{\partial s}}
(u_s\cos\theta-u_n\sin\theta)
+\cos\theta u_n{{\partial}\over{\partial n}}
(u_s\cos\theta-u_n\sin\theta)\\& +\sin\theta{{\partial v}\over{\partial t}}
+\sin\theta u_s {{\partial}\over{\partial s}}
(u_s\sin\theta+u_n\cos\theta)
+\sin\theta u_n {{\partial}\over{\partial n}}
(u_s\sin\theta+u_n\cos\theta)\\= & {{\partial u_s}\over{\partial t}}
+u_s\cos^2\theta {{\partial u_s}\over{\partial s}}
+u_s^2\cos\theta{{\partial(\cos\theta)}\over{\partial s}}
-u_s\sin\theta \cos\theta{{\partial u_n}\over{\partial s}}
-u_s u_n\cos\theta{{\partial(\sin\theta)}\over{\partial s}}\\& +u_n\cos^2\theta {{\partial u_s}\over{\partial n}}
+u_s u_n\cos\theta{{\partial(\cos\theta)}\over{\partial n}}
-u_n\sin\theta \cos\theta{{\partial u_n}\over{\partial n}}
-u_n^2\cos\theta{{\partial(\sin\theta)}\over{\partial n}}\\& +u_s\sin^2\theta {{\partial u_s}\over{\partial s}}
+u_s^2\sin\theta{{\partial(\sin\theta)}\over{\partial s}}
+u_s\sin\theta \cos\theta{{\partial u_n}\over{\partial s}}
+u_s u_n\sin\theta{{\partial(\cos\theta)}\over{\partial s}}\\& +u_n\sin^2\theta {{\partial u_s}\over{\partial n}}
+u_s u_n\sin\theta{{\partial(\sin\theta)}\over{\partial n}}
+u_n\sin\theta \cos\theta{{\partial u_n}\over{\partial n}}
+u_n^2\sin\theta{{\partial(\cos\theta)}\over{\partial n}}\\= & {{\partial u_s}\over{\partial t}}
+u_s{{\partial u_s}\over{\partial s}}
+u_n{{\partial u_s}\over{\partial n}}\\& +u_s^2\cos\theta{{\partial(\cos\theta)}\over{\partial s}}
-u_s u_n\cos\theta{{\partial(\sin\theta)}\over{\partial s}}
+u_s u_n\cos\theta{{\partial(\cos\theta)}\over{\partial n}}
-u_n^2\cos\theta{{\partial(\sin\theta)}\over{\partial n}}\\& +u_s^2\sin\theta{{\partial(\sin\theta)}\over{\partial s}}
+u_s u_n\sin\theta{{\partial(\cos\theta)}\over{\partial s}}
+u_s u_n\sin\theta{{\partial(\sin\theta)}\over{\partial n}}
+u_n^2\sin\theta{{\partial(\cos\theta)}\over{\partial n}}\\= & {{\partial u_s}\over{\partial t}}
+u_s{{\partial u_s}\over{\partial s}}
+u_n{{\partial u_s}\over{\partial n}}
+u_s^2\left\{\sin\theta{{\partial(\sin\theta)}\over{\partial s}}
+\cos\theta{{\partial(\cos\theta)}\over{\partial s}}\right\}\\& +u_s u_n\left\{
\cos\theta{{\partial(\cos\theta)}\over{\partial n}}
-\cos\theta{{\partial(\sin\theta)}\over{\partial s}}
+\sin\theta{{\partial(\cos\theta)}\over{\partial s}}
+\sin\theta{{\partial(\sin\theta)}\over{\partial n}}
\right\}\\& +u_n^2\left\{
\sin\theta{{\partial(\cos\theta)}\over{\partial n}}
-\cos\theta{{\partial(\sin\theta)}\over{\partial n}}
\right\}\end{aligned}\end{align} \]
Where,
(94) \[\sin\theta{{\partial(\sin\theta)}\over{\partial s}}
+\cos\theta{{\partial(\cos\theta)}\over{\partial s}}
=\sin\theta\cos\theta{{\partial \theta}\over{\partial s}}
-\cos\theta\sin\theta{{\partial \theta}\over{\partial s}}=0\]
(95) \[ \begin{align}\begin{aligned}& \cos\theta{{\partial(\cos\theta)}\over{\partial n}}
-\cos\theta{{\partial(\sin\theta)}\over{\partial s}}
+\sin\theta{{\partial(\cos\theta)}\over{\partial s}}
+\sin\theta{{\partial(\sin\theta)}\over{\partial n}}\\= & \cancel{-\cos\theta\sin\theta{{\partial \theta}\over{\partial n}}}
-\cos^2\theta{{\partial \theta}\over{\partial s}}
-\sin^2\theta{{\partial \theta}\over{\partial s}}
\cancel{+\sin\theta\cos\theta{{\partial \theta}\over{\partial n}}}\\= &-\left(\cos^2\theta+\sin^2\theta\right){{\partial \theta}\over{\partial s}}\\= &-{{\partial \theta}\over{\partial s}}=-{1 \over r}\end{aligned}\end{align} \]
Also,
(96) \[\sin\theta{{\partial(\cos\theta)}\over{\partial n}}
-\cos\theta{{\partial(\sin\theta)}\over{\partial n}}=
-\sin^2\theta{{\partial \theta}\over{\partial n}}
-\cos^2\theta{{\partial \theta}\over{\partial n}}
=-{{\partial \theta}\over{\partial n}}=0\]
Therefore, the advection term in the \(s\) axis direction is as follows.
(97) \[A_s=
{{\partial u_s}\over{\partial t}}
+u_s{{\partial u_s}\over{\partial s}}
+u_n{{\partial u_s}\over{\partial n}}
-{{u_s u_n}\over{r}}\]
Acceleration in the transverse direction
Acceleration in the channel transverse direction, \(n\) axis directions can be written as,
(98) \[ \begin{align}\begin{aligned}A_n = & -A_x\sin\theta+A_y\cos\theta
\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad\\= & -\left(
{{\partial u_x}\over{\partial t}}+
u_s{{\partial u_x}\over{\partial s}}
+u_n{{\partial u_x}\over{\partial n}}
\right)\sin\theta+
\left(
{{\partial u_y}\over{\partial t}}+
u_s{{\partial u_y}\over{\partial s}}
+u_n{{\partial u_y}\over{\partial n}}
\right)\cos\theta\\= & {{\partial u_n}\over{\partial t}}
-\sin\theta u_s {{\partial}\over{\partial s}}
(u_s\cos\theta-u_n\sin\theta)
-\sin\theta u_n{{\partial}\over{\partial n}}
(u_s\cos\theta-u_n\sin\theta)\\& +\cos\theta u_s {{\partial}\over{\partial s}}
(u_s\sin\theta+u_n\cos\theta)
+\cos\theta u_n {{\partial}\over{\partial n}}
(u_s\sin\theta+u_n\cos\theta)\\= & {{\partial u_n}\over{\partial t}}
-u_s\sin\theta\cos\theta {{\partial u_s}\over{\partial s}}
-u_s^2\sin\theta{{\partial(\cos\theta)}\over{\partial s}}
+u_s\sin^2\theta {{\partial u_n}\over{\partial s}}
+u_s u_n\sin\theta{{\partial(\sin\theta)}\over{\partial s}}\\& -u_n\sin\theta\cos\theta {{\partial u_s}\over{\partial n}}
-u_s u_n\sin\theta{{\partial(\cos\theta)}\over{\partial n}}
+u_n\sin^2\theta {{\partial u_n}\over{\partial n}}
+u_n^2\sin\theta{{\partial(\sin\theta)}\over{\partial n}}\\& +u_s\cos\theta\sin\theta {{\partial u_s}\over{\partial s}}
+u_s^2\cos\theta{{\partial(\sin\theta)}\over{\partial s}}
+u_s\cos^2\theta{{\partial u_n}\over{\partial s}}
+u_s u_n\cos\theta{{\partial(\cos\theta)}\over{\partial s}}\\& +u_n\sin\theta\cos\theta {{\partial u_s}\over{\partial n}}
+u_s u_n\cos\theta{{\partial(\sin\theta)}\over{\partial n}}
+u_n\cos^2\theta{{\partial u_n}\over{\partial n}}
+u_n^2\cos\theta{{\partial(\cos\theta)}\over{\partial n}}\\= & {{\partial u_n}\over{\partial t}}
+u_s{{\partial u_n}\over{\partial s}}
+u_n{{\partial u_n}\over{\partial n}}\\& -u_s^2\sin\theta{{\partial(\cos\theta)}\over{\partial s}}
+u_s u_n\sin\theta{{\partial(\sin\theta)}\over{\partial s}}
-u_s u_n\sin\theta{{\partial(\cos\theta)}\over{\partial n}}
+u_n^2\sin\theta{{\partial(\sin\theta)}\over{\partial n}}\\& +u_s^2\cos\theta{{\partial(\sin\theta)}\over{\partial s}}
+u_s u_n\cos\theta{{\partial(\cos\theta)}\over{\partial s}}
+u_s u_n\cos\theta{{\partial(\sin\theta)}\over{\partial n}}
+u_n^2\cos\theta{{\partial(\cos\theta)}\over{\partial n}}\\= & {{\partial u_n}\over{\partial t}}
+u_s{{\partial u_n}\over{\partial s}}
+u_n{{\partial u_n}\over{\partial n}}
+u_s^2\left\{-\sin\theta{{\partial(\cos\theta)}\over{\partial s}}
+\cos\theta{{\partial(\sin\theta)}\over{\partial s}}\right\}\\& +u_s u_n\left\{
\sin\theta{{\partial(\sin\theta)}\over{\partial s}}
-\sin\theta{{\partial(\cos\theta)}\over{\partial n}}
+\cos\theta{{\partial(\cos\theta)}\over{\partial s}}
+\cos\theta{{\partial(\sin\theta)}\over{\partial n}}
\right\}\\& +u_n^2\left\{
\sin\theta{{\partial(\sin\theta)}\over{\partial n}}
+\cos\theta{{\partial(\cos\theta)}\over{\partial n}}
\right\}\end{aligned}\end{align} \]
Where,
(99) \[-\sin\theta{{\partial(\cos\theta)}\over{\partial s}}
+\cos\theta{{\partial(\sin\theta)}\over{\partial s}}
=\sin^2\theta{{\partial \theta}\over{\partial s}}
+\cos^2\theta{{\partial \theta}\over{\partial s}}={1 \over r}\]
(100) \[ \begin{align}\begin{aligned}& \sin\theta{{\partial(\sin\theta)}\over{\partial s}}
-\sin\theta{{\partial(\cos\theta)}\over{\partial n}}
+\cos\theta{{\partial(\cos\theta)}\over{\partial s}}
+\cos\theta{{\partial(\sin\theta)}\over{\partial n}}\\= & \cancel{\sin\theta\cos\theta{{\partial \theta}\over{\partial s}}}
+\sin^2\theta{{\partial \theta}\over{\partial n}}
\cancel{-\sin\theta\cos\theta{{\partial \theta}\over{\partial s}}}
+\cos^2\theta{{\partial \theta}\over{\partial n}}\\= & {{\partial \theta}\over{\partial n}}=0\end{aligned}\end{align} \]
(101) \[\sin\theta{{\partial(\sin\theta)}\over{\partial n}}
+\cos\theta{{\partial(\cos\theta)}\over{\partial n}}=
\sin\theta\cos\theta{{\partial \theta}\over{\partial n}}
-\sin\theta\cos\theta{{\partial \theta}\over{\partial n}}
=0\]
Therefore, the advection term in the \(n\) axis direction is as follows.
(102) \[A_n=
{{\partial u_n}\over{\partial t}}
+u_s{{\partial u_n}\over{\partial s}}
+u_n{{\partial u_n}\over{\partial n}}
+{{u_s^2}\over{r}}\]
Pressure term
The pressure gradient in the \(x,y\) axis directions are…
(103) \[ \begin{align}\begin{aligned}P_x= & -g\cfrac{\partial H}{\partial x}
=-g\left(\cos\theta\cfrac{\partial H}{\partial s}
-\sin\theta\cfrac{\partial H}{\partial n}
\right)\\P_y= & -g\cfrac{\partial H}{\partial y}
=-g\left(\sin\theta\cfrac{\partial H}{\partial s}
+\cos\theta\cfrac{\partial H}{\partial n}
\right)\end{aligned}\end{align} \]
Convert these to the pressure gradients, \(P_s, P_n\) , in the \(s, n\) axis directions.
(104) \[\begin{split}P_s= & P_x \cos\theta+P_y \sin\theta \\
= & \cos\theta\left\{
-g\left(\cos\theta\cfrac{\partial H}{\partial s}
-\sin\theta\cfrac{\partial H}{\partial n}
\right)
\right\}
+\sin\theta\left\{
-g\left(\sin\theta\cfrac{\partial H}{\partial s}
+\cos\theta\cfrac{\partial H}{\partial n}
\right)
\right\} \\
= & g\left(
-\cos^2\theta\cfrac{\partial H}{\partial s}
\cancel{+\cos\theta\sin\theta\cfrac{\partial H}{\partial n}}
-\sin^2\theta\cfrac{\partial H}{\partial s}
\cancel{-\cos\theta\sin\theta\cfrac{\partial H}{\partial n}}
\right) \\
= & -g\cfrac{\partial H}{\partial s}\end{split}\]
(105) \[\begin{split}P_n= & -P_x \sin\theta+P_y \cos\theta \\
= & -\sin\theta\left\{
-g\left(\cos\theta\cfrac{\partial H}{\partial s}
-\sin\theta\cfrac{\partial H}{\partial n}
\right)
\right\}
+\cos\theta\left\{
-g\left(\sin\theta\cfrac{\partial H}{\partial s}
+\cos\theta\cfrac{\partial H}{\partial n}
\right)
\right\} \\
= & g\left(
\cancel{\cos\theta\sin\theta\cfrac{\partial H}{\partial s}}
-\sin^2\theta\cfrac{\partial H}{\partial n}
\cancel{-\cos\theta\sin\theta\cfrac{\partial H}{\partial s}}
-\cos^2\theta\cfrac{\partial H}{\partial s}
\right) \\
=& -g\cfrac{\partial H}{\partial n}\end{split}\]
Friction term
From (13) , when Manning’s law is adopted, the friction term in the \(x,y\) axis directions are expressed as follows:
(106) \[ \begin{align}\begin{aligned}F_x = & -\cfrac{\tau_x}{\rho h}
= -{{g n_m^2 u \sqrt{u^2+v^2}}\over h^{4/3}} =-u V_\tau\\F_y = & -\cfrac{\tau_y}{\rho h}
= -{{g n_m^2 u \sqrt{u^2+v^2}}\over h^{4/3}} =-v V_\tau\end{aligned}\end{align} \]
Where,
(107) \[V_\tau = \cfrac{g n_m^2 \sqrt{u^2+v^2}}{h^{4/3}}
= \cfrac{g n_m^2 \sqrt{u_s^2+u_n^2}}{h^{4/3}}\]
Convert Equation (106) to the \(s,n\) axis directions.
Assume \(F_s, F_n\) are the friction term in the \(s, n\) directions.
(108) \[ \begin{align}\begin{aligned}F_s & = F_x\cos\theta+F_y\sin\theta = -u V_\tau\cos\theta-v V_\tau\sin\theta\\& = -(u_s \cos \theta - u_n \sin \theta)V_\tau\cos\theta
-(u_s \sin \theta + u_n \cos \theta) V_\tau\sin\theta\\& = -u_s V_\tau \cos^2 \theta \cancel{- u_n V_\tau \sin\theta\cos\theta}
-u_s V_\tau \sin^2\theta +\cancel{u_n V_\tau \sin\theta\cos\theta}\\& = -u_s(\sin^2\theta+\cos^2 \theta)V_\tau = -u_s V_\tau
=-{{g n_m^2 u_s \sqrt{u_s^2+u_n^2}}\over h^{4/3}}\end{aligned}\end{align} \]
(109) \[ \begin{align}\begin{aligned}F_n & = -F_x\sin\theta+F_y\cos\theta =u V_\tau\sin\theta-v V_\tau\cos\theta\\& = (u_s \cos\theta - u_n \sin \theta)V_\tau\sin\theta
-(u_s \sin \theta + u_n \cos \theta)V_\tau\cos\theta\\& = \cancel{u_s V_\tau\cos\theta\sin\theta}-u_nV_\tau\sin^2\theta
-\cancel{u_s V_\tau\sin\theta\cos\theta}-u_nV_\tau\cos^2\theta\\& = -u_n(\sin^2\theta+\cos^2 \theta)V_\tau = -u_n V_\tau
=-{{g n_m^2 u_n \sqrt{u_s^2+u_n^2}}\over h^{4/3}}\end{aligned}\end{align} \]
Diffusion term
Similar to the density diffusion equation (Equation (119) ) on the \(s-n\) coordinates, the diffusion of momentums are expressed as follows.
(110) \[ \begin{align}\begin{aligned}D_s & =
\cfrac{\partial}{\partial s}\left(\nu_t\cfrac{\partial u_s}{\partial s}\right)
+\cfrac{\partial}{\partial n}\left(\nu_t\cfrac{\partial u_s}{\partial n}\right)
+\cfrac{\nu_t}{r}\cfrac{\partial u_s}{\partial n}\\D_n & =\cfrac{\partial}{\partial s}\left(\nu_t \cfrac{\partial u_n}{\partial s}\right)
+\cfrac{\partial}{\partial n}\left(\nu_t\cfrac{\partial u_n}{\partial n}\right)
+\cfrac{\nu_t}{r}\cfrac{\partial u_n}{\partial n}\end{aligned}\end{align} \]
Summary
The equations of motion and the equations of continuity of 2D free surface flow on the \(s-n\) coordinates are as follows.
(111) \[\cfrac{\partial h}{\partial t}
+\cfrac{\partial(hu_s)}{\partial s}
+\cfrac{1}{r}\cfrac{\partial(rhu_n)}{\partial n} =0\]
(112) \[ \begin{align}\begin{aligned}{{\partial u_s}\over{\partial t}}
+u_s{{\partial u_s}\over{\partial s}}
+u_n{{\partial u_s}\over{\partial n}}
-{{u_s u_n}\over{r}}= \hspace{4.5cm}\\-g\cfrac{\partial H}{\partial s}
-{{g n_m^2 u_s \sqrt{u_s^2+u_n^2}}\over h^{4/3}}
+\cfrac{\partial}{\partial s}\left(\nu_t\cfrac{\partial u_s}{\partial s}\right)
+\cfrac{\partial}{\partial n}\left(\nu_t\cfrac{\partial u_s}{\partial n}\right)
+\cfrac{\nu_t}{r}\cfrac{\partial u_s}{\partial n}\end{aligned}\end{align} \]
(113) \[ \begin{align}\begin{aligned}{{\partial u_n}\over{\partial t}}
+u_s{{\partial u_n}\over{\partial s}}
+u_n{{\partial u_n}\over{\partial n}}
+{{u_s^2}\over{r}}= \hspace{4.5cm}\\-g\cfrac{\partial H}{\partial n}
-{{g n_m^2 u_n \sqrt{u_s^2+u_n^2}}\over h^{4/3}}
+\cfrac{\partial}{\partial s}\left(\nu_t \cfrac{\partial u_n}{\partial s}\right)
+\cfrac{\partial}{\partial n}\left(\nu_t\cfrac{\partial u_n}{\partial n}\right)
+\cfrac{\nu_t}{r}\cfrac{\partial u_n}{\partial n}\end{aligned}\end{align} \]